A. Bowyer
巴斯大学数学系,Claverton Down,巴斯 BA2 7AY
本文提出了一种高效算法,用于计算 维欧几里得空间()中的 Dirichlet 镶嵌和 Delaunay 三角剖分。该算法的设计方式使其有望扩展到某些较简单的非欧几里得度量空间。作者已用 ISO FORTRAN 实现了该算法,本文末尾给出了执行时间以及镶嵌和三角剖分的立体图像。(1980年4月收稿)
1. 引言
1.1 定义
假设平面上给定 个互异点 的位置作为数据。我们可以为每个点分配一个“领地”,即平面上比其他任何数据点更接近该点的区域。由此形成的领地将构成一个覆盖整个平面的凸多边形密铺图案。这种结构称为这些点的 Dirichlet 镶嵌。图1(引自 Green 和 Sibson,1978)展示了少量点()的 Dirichlet 镶嵌(粗线)。位于凸包上的某些数据点将拥有无限大的领地,其余点则拥有有限的领地。
根据上述定义,构成领地边界的直线段必定位于其两侧两点的正中间。每一段领地边界都是连接这两个点的线段的垂直平分线的一部分。若将所有共享某段边界的点对用直线连接起来,结果便是数据点凸包的一个三角剖分。这种三角剖分称为 Delaunay 三角剖分。在图1中,Delaunay 三角剖分以细线表示。在 Delaunay 三角剖分中由线段连接的点对被称为相邻点。Green 和 Sibson(1978)已发表了一种高效的二维算法来计算这些结构,其时间复杂度为 ,可进一步优化至 。
上述定义可推广至任意维度的欧几里得空间。本文旨在解决在任意维欧几里得空间中计算 Dirichlet 镶嵌和 Delaunay 三角剖分的问题。经过适当处理,该算法也可能适用于某些性质较好的非欧几里得度量空间(例如球面)。
Brown(1979)提到,可通过 维空间中凸包的变换来计算 维空间中的镶嵌。然而,由于缺乏通用的凸包算法,目前尚不清楚如何实现这一方法。实际上,或许可以执行相反的操作:从 维 Dirichlet 镶嵌出发计算凸包。
1.2 性质
在二维情形下,领地的顶点出现在三条领地边界交汇之处(退化情形除外,见第3.1节)。围绕一个顶点的三个领地分别属于构成一个 Delaunay 三角形的三个点。根据镶嵌的定义,该顶点到这三个点的距离相等,即为对应 Delaunay 三角形的外心。每个 Delaunay 三角形在镶嵌中对应唯一一个顶点,反之亦然。
于2014年8月21日从 http://comjl.oxfordjournals.org/ 下载,来源:马萨诸塞大学 Healey 图书馆
在 维欧几里得空间中,Delaunay 三角形推广为以 个数据点为顶点的单纯形。镶嵌中的每个顶点是 个领地的交汇点,同时也是通过对应单纯形所有顶点的超球面的球心。与之前类似,每对相邻点由一条线段连接,该线段是某些 Delaunay 单纯形的一条边。相邻点对共享的领地边界是一个位于 维超平面中的凸多边形,该超平面平分连接这对点的边。
在三维空间中,每个数据点的领地是一个凸多面体,即空间中比其他任何点更接近该点的区域。这些多面体的面是凸多边形,即相邻点共享的领地边界。每个凸多边形位于某个 Delaunay 四面体一条边的中垂面内。图2展示了一个三维顶点及其对应的 Delaunay 四面体。
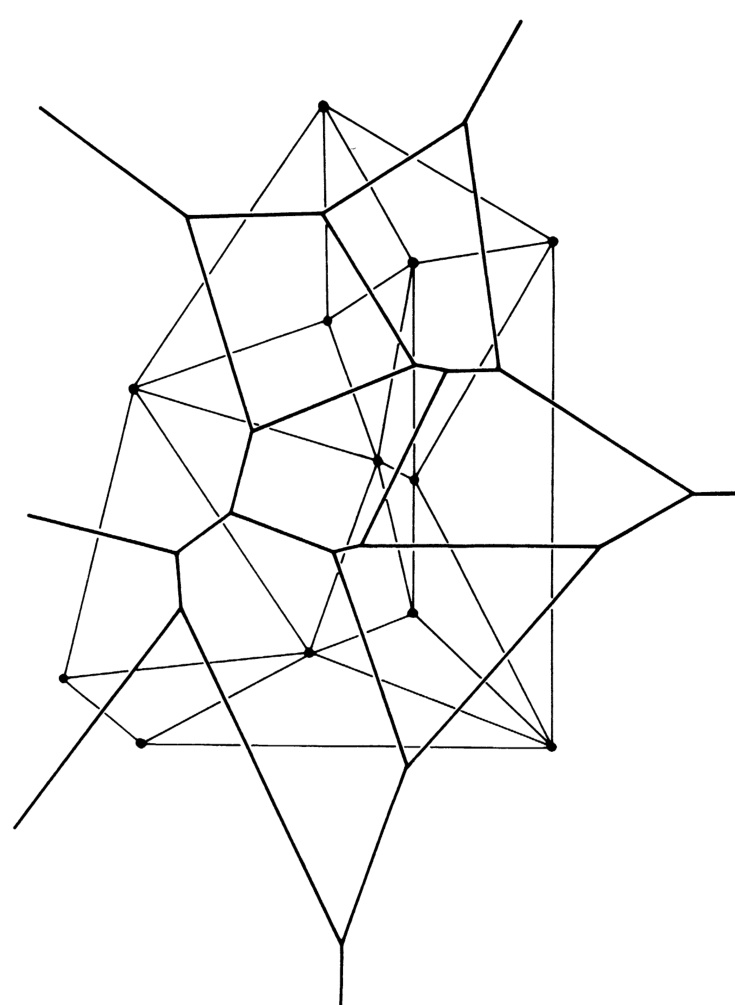
图1 小规模点集的 Dirichlet 镶嵌(粗线)与 Delaunay 三角剖分(细线),引自 Green 和 Sibson(1978)
†编者注:本文与 Watson 的文章(本期)在部分内容上有所重叠。由于这两篇稿件几乎同时收到,编者认为应同时刊载两文。
1.3 应用
过去几年中,高效的二维 Dirichlet 镶嵌算法的出现,使得人们能够研究一些早于该算法提出的镶嵌应用,并开拓了一些新的应用领域。其中大多数并非严格局限于二维问题。
Green(私人通信)利用该结构模拟了随机细胞模式中传染病的传播。人们对于传染病在规则格点上的传播已有较多了解。而随机点过程的某些实现所产生的 Delaunay 三角剖分和 Dirichlet 镶嵌,为这类研究提供了一种具有多种优良性质的随机格点。
该二维结构的一个显而易见的应用是研究动物的领地行为。
在更抽象的层面上,这些结构在某些空间点过程的分析与模拟中十分有用(参见 Miles,1970;Ripley,1977)。晶体学家使用的一种晶体生长模型需要用到三维 Dirichlet 镶嵌(Gilbert,1962)。地理学家也出于多种目的使用这些结构。
Lawson(1972)提出了一种用于插值和有限元分析的三角剖分最优性准则。Sibson(1978)证明了 Delaunay 三角剖分是唯一满足该准则的三角剖分。
Dirichlet 镶嵌最重要的应用之一,是在不规则观测点上对某函数(例如气压或海拔高度)进行曲面拟合与平滑处理(Sibson,1980)。能够适用于高维空间的镶嵌/三角剖分算法的出现,将使这类工作得以扩展到两个以上自变量的情形。
由于本文提出的算法旨在处理任意维度的凸多边形,因此很可能在某些线性规划问题中发挥作用。该算法也可能有助于计算高维数据点集的凸包(Green 和 Silverman,1979;Brown,1979)。
2. 算法
2.1 数据结构
在考虑如何计算该结构之前,必须先决定如何存储它。Green 和 Sibson 将 Delaunay 三角剖分以每个点对应的连续点列表形式进行存储。他们的算法利用了这样一个事实:在二维情形下,这些列表可以循环存储,从而便于逐个将点插入结构中。在更高维的情形下,无法将邻接列表按循环顺序排列,但或许可以采用其他方式组织这些列表(例如,按照列表中各邻接点到该点的距离递增排序)。
假设我们希望存储该镶嵌(tessellation)的顶点结构。考虑图 3。图中平面上的八个数据点产生了七个顶点 。那些延伸至无穷远的区域边界可以方便地视为终止于一个标记为 0 的顶点。每个顶点都是三个数据点的外心,因此可以为每个顶点记录这三个数据点。此外,每个顶点还指向另外三个顶点,每个顶点分别位于其构成点之一的对侧。
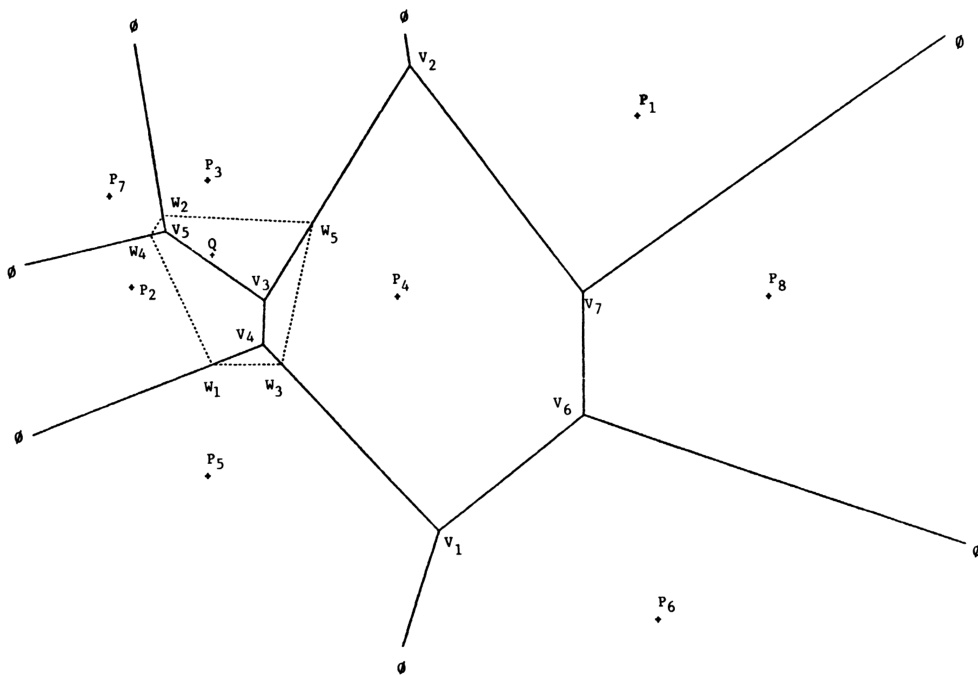
图 3 查找点 所属区域的算法
于 2014 年 8 月 21 日从 http://comjnl.oxfordjournals.org/ 下载,来源:马萨诸塞大学 Healey 图书馆
| 顶点 | 构成点 | 相邻顶点 | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | |
| 0 | ||||||
| 0 | ||||||
| 0 | ||||||
| 0 | 0 | |||||
| 0 | ||||||
| 0 | ||||||
构成点。因此,可以通过为结构中的每个顶点构建两个长度为三的列表来记录该结构:一个列表存储该顶点的构成点(即 Delaunay 三角形),另一个列表存储其对侧的相邻顶点(见表 1)。在下文描述的算法中,顶点周围点的循环顺序方向无关紧要,因此表 1 中的顺序是故意任意的。
在 维空间中,每个顶点将有 个构成点和 个对侧的相邻顶点。
2.2 添加一个点
如果能够以上述方式记录结构,然后添加一个新的数据点并相应地修改记录,那么就可以从一个简单结构开始,逐步构建,从而对任意数量的点进行镶嵌和三角剖分。显然的初始模式是由前 个点构成的 Delaunay 单形(simplex)。这将产生一个仅包含一个真实顶点的镶嵌,该顶点的所有相邻顶点均为 。此处唯一的限制是,最初的 个点不能全部位于所考虑的 维空间中的同一超平面上。这通常不会构成严重限制。
假设我们希望在当前数据点的凸包内部插入一个新点(如图 3 中的 )。我们希望找到的区域由虚线标出。实现此目的的算法可概述如下:
-
识别当前结构中将被新点删除的一个顶点(例如 )。这样的顶点是指其到新点的距离小于到其构成点的距离的任意顶点。这样的顶点至少存在一个,因为新点所在的 Delaunay 单形对应的顶点总是会被删除,而 Delaunay 单形完全填充了当前已包含点的凸包。
-
从被删除的顶点开始,对顶点结构执行树搜索,寻找其他将被删除的顶点。如果数据按表 1 所示方式存储,这将非常容易。结果将得到一个由新点 删除的所有顶点列表。在此例中,该列表为:。
-
与 相邻的点是所有被删除顶点的构成点:。
-
如果某对相邻点之间的旧邻接关系(例如 )的所有顶点(如 )均在被删除顶点列表中,则该邻接关系将被移除。
-
在此例中,新点关联五个新顶点:。计算它们的构成点和相邻顶点。每个新顶点的构成点包括点 和 个与 相邻的点。镶嵌中的每条边周围有 个点(例如,边 由 和 构成)。新顶点的构成点及其相邻顶点可通过考察被删除顶点列表中指向的、但自身未被删除的顶点,并找出围绕这些顶点的点环来确定。例如, 从 指向外侧的 ,其构成点为 。
-
最后一步是将部分新顶点复制到被删除顶点的位置,以节省空间。
注意,除第一步外,所有这些操作都是局部的,其执行时间与结构中当前点的数量无关。所需工作量大致与创建的新顶点数量成正比。给定维度 ,一个点所属区域边界上的期望顶点数是常数。在二维情形下,可利用多面体的 Euler-Poincaré 公式(关于面、边和顶点)证明每个区域的期望顶点数恰好为六。在三维情形下,Miles (1970) 给出了泊松点过程下每个区域期望顶点数的上界为 27.07。遗憾的是,目前尚无适用于 维情形下该数值的一般表达式。
因此,给定维度 和第一步,插入一个点所需的工作量是常数,从而对 个点计算整个结构的时间复杂度为 。那么,如何为第一步识别出一个将被删除的顶点呢?
显然,可以检查结构中的每个顶点,看其是否比其构成点更接近新点。然而,这一过程耗时(尤其在高维且点数众多时),会削弱插入算法局部性带来的优势。
若能无需检查结构中大多数顶点即可识别出一个被删除的顶点,将大有裨益。如何做到这一点?Green 和 Sibson 针对二维情形提出的算法首先找到当前结构中距离待插入点最近的邻接点,即新点所处区域对应的当前已接受点。他们通过从某个已接受点出发,在 Delaunay 三角剖分中逐邻接点“行走”(walk)直至接近新点,从而找到该最近邻点。若无其他信息,显然应从当前已接受点质心附近的一个点开始行走;在二维情形下,该行走过程耗时 。显然,若已知新点很可能靠近刚刚插入的点,则从该点开始行走将带来可忽略的计算开销。
在 维情形下,从构型质心出发的行走应耗时 。
一旦找到新点的最近邻点,找到一个被删除的顶点就很简单了。新点至少会删除其最近邻点区域边界上的一个顶点。该方法的一个特点是,必须为结构中的每个点维护其相邻点列表,以便轻松执行行走操作。这些列表在算法完成后可能非常有用,且易于计算和维护(见步骤 3 和 4)。如果能直接通过表 1 中存储的顶点结构进行行走以找到被删除的顶点,从而无需维护单独的邻接列表,那就更好了。从构型质心附近的某个顶点出发,在顶点结构中行走以找到距离新点最近的顶点是很容易的。不幸的是,该顶点未必会被新点删除,作者尚未能设计出一条简单的规则来找到附近一个确实会被删除的顶点。
最后,在算法概述的开头提到,该算法适用于在当前点集凸包内部插入点。这是因为凸包外部的新点可能不会删除任何顶点,因而需特殊处理。这种情况很容易检测:新点的最近邻点的所有顶点均未被删除,这一点很容易判断。解决此困难的最简单方法是设置算法所基于的初始单形及其顶点,使得该单形角点上的 个点在整个过程中始终保持为凸包。由于浮点数的整个取值范围都可用,即使对于最不寻常的数据,这也并不困难。这最初的 个点几乎总是非实际数据值,而是人为生成以界定问题范围的点。
3. 实现
3.1 退化(Degeneracy)
在二维情形下,当结构中四个(或更多)点共圆时会发生退化,此时它们的四个区域在一个点处相交。在更高维情形下,可能出现更微妙的退化;例如,在三维情形下,Dirichlet 镶嵌中四个点可能共线。
退化本身在数据中实际出现时问题不大,真正的问题在于计算机中的舍入误差可能导致算法在接近退化的情形下失败,例如使点 与点 相邻,但 却不与 相邻。在上述算法的哪些步骤中,退化和近似退化会成为问题?
只要待插入的新点位于当前凸包内部,第一步中寻找被删除顶点就不会有任何困难。唯一可能出现的问题是新点与已有某点重合——这很容易避免,只需在步骤2–6考虑接纳新点之前,要求每个新点与其最近邻点之间至少保持某个微小距离即可。需要记住的是,初始对镶嵌(tessellation)的定义就要求所有点互不相同。
步骤2中的树搜索是算法中唯一仍需进行浮点运算的阶段。一旦找到被删除顶点的列表,其余操作就完全是逻辑性的了。每个被考虑加入删除顶点列表的候选顶点仅被检查一次。将候选顶点作为中心的超球体的半径平方,与其到新点距离的平方进行比较(无需比较实际欧几里得距离——开平方会浪费时间)。如果新点比构成该顶点的原始点更靠近该顶点,则将该顶点加入删除顶点列表;否则忽略该顶点。唯一可能出现的问题是当半径平方与距离平方相等(或近似相等)时。此时可以选择是否将该顶点包含在列表中。如果包含该候选顶点,则镶嵌中沿树搜索路径到达该顶点所经过的边对面的那个点,将被视为与新点相邻,但它们之间的区域边界面积为零。也就是说,新点区域中对应于该相邻关系的面将是一个具有 个顶点的多边形,而这些顶点全部位于同一位置。注意:
- 结构的逻辑性仍得以保持,因此计算可以继续进行。
- 计算这些重合顶点的位置不存在数值困难。
上述论证可推广至多重退化情形。程序逻辑能够保持数据结构为一个有效的镶嵌,并且在需要计算退化顶点位置时,绝不会出现诸如除零之类的数值问题。若候选顶点被排除在删除顶点列表之外,也会产生类似情况,只不过此时镶嵌中会出现一条长度为零的边(事实上,作者在其实现中正是采用这种处理方式),而非面积为零的面。
第二种退化情形发生在 (或更多)个点共处于一个超平面且共圆时。除非数据点被刻意放置在规则网格上(此时通常可显式写出结构),否则这种事件极不可能发生。然而一旦出现此类构型,可能会引发问题:在尝试插入这 个点中的最后一个点时,由前 个点定义的镶嵌边一端的顶点可能被加入删除列表,而另一端的顶点却未被加入。此时程序将面临沿该边某处寻找一个新顶点的问题,而该顶点的位置实际上就是该边与自身相交之处。显然,程序在此处可能失败。幸运的是,这一问题也可克服:只需在发生这种情况时加以标记(即标记为程序无法计算此类顶点的位置),并始终将该顶点包含在删除列表中。这样就将问题简化为第一类退化情形。
作者的算法已在高度退化的点模式上成功运行(例如,可在三维球面上通过使用3、4、5个三角形获得的点集)。
3.2 编程实现
该算法已实现为一组ISO FORTRAN子程序,可由一个简单的主程序逐个传入点来调用。在整个过程中,用户在任何阶段均可访问完整的顶点列表和Delaunay单纯形数据结构。此外,还编写了多种实用子程序,用于生成围绕某点区域的顶点列表,或两个点共有的顶点列表(即与相邻关系相关的顶点)。该软件包约包含900行代码,其中约三分之一为注释。
通常可在存储空间与执行时间之间进行权衡。例如,可以选择在结构中存储每个顶点的位置及其半径平方,也可以在需要时再计算这些值。
于2014年8月21日从 http://comjnl.oxfordjournals.org/ 下载,来源:马萨诸塞大学Healey图书馆
在作者对该算法的实现中,所有浮点运算都被限制在两个子程序内:一个用于计算镶嵌所在 维空间中任意两点间的距离平方,另一个用于计算通过单纯形 个顶点的超球体的外心(circumcentre)及其半径平方。
这意味着,只要采取一些预防措施,仅通过修改这两个子程序,该算法即可应用于非欧几里得空间。例如,在球面上,三个初始点会产生两个顶点;而在平面上,三个点仅产生一个顶点。
3.3 图示
前文已给出两个二维结构的图示。计算出三维结构后,对数据点和镶嵌顶点的坐标进行处理,从某一视点生成该结构的透视图像是一件简单的事情。若将视点稍作移动并生成另一幅图像,即可得到一对立体图像。图4展示了立方体内20个点的镶嵌立体图像对。其中19个点按立方体上的均匀分布生成,第20个点置于立方体中心。第20个点及其对应区域用比结构其余部分更粗的线条绘制,以便更清晰地观察一个完整的区域。图5展示了对应的Delaunay四面体。
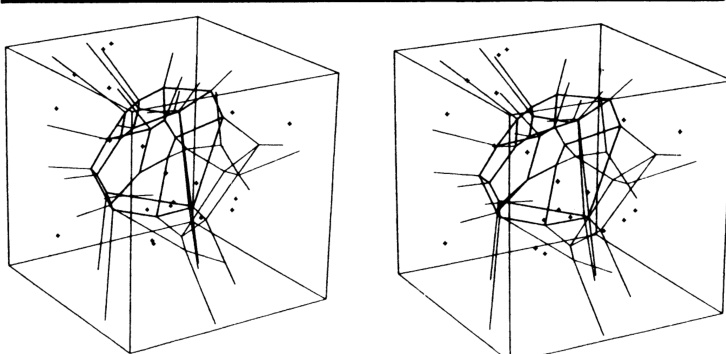
图4 三维Dirichlet镶嵌
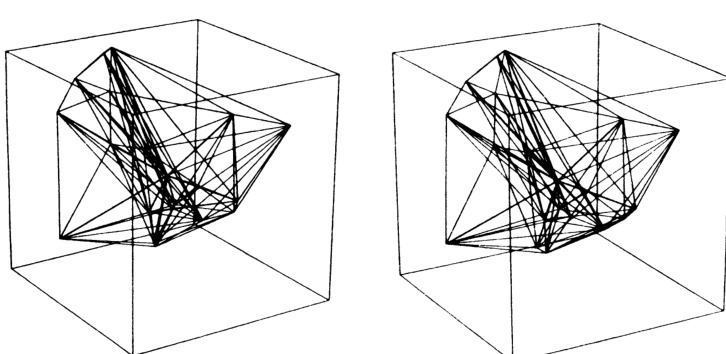
图5 三维Delaunay三角剖分
同样,中心点的所有相邻关系均用粗线绘制。如果读者没有立体镜,通常可通过在页面上左右眼图像之间放置一张卡片,放松双眼使两幅图像重合,然后尝试聚焦于合成后的单一图像来观察三维效果。该过程的难点在于第二步:人脑在生命早期就学会了将双眼夹角与晶状体所需形变量关联起来以生成清晰图像。一种解决方案是使用两个相同的放大镜,每只眼前各放一个。这样可使双眼既聚焦于无穷远,又指向无穷远,而实际上是从较近距离观察图像。
图4和图5的原始绘图使用颜色区分结构的不同部分。遗憾的是,由于印刷困难,此处无法再现彩色图像。
3.4 运行时间
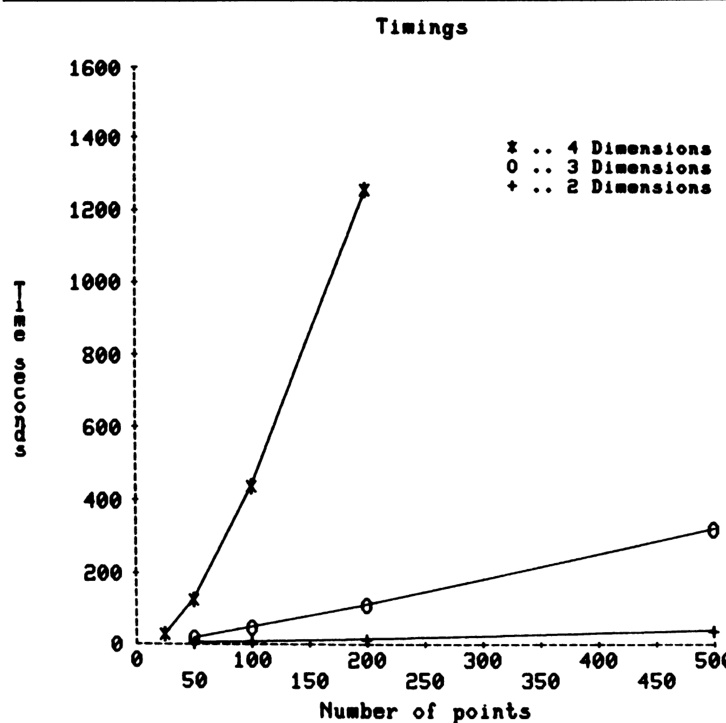
如前所述,寻找初始待删除顶点所需的工作量为 。对于 维空间中的 个点,这将导致镶嵌计算总时间中出现 项。一旦找到这样一个顶点,每个点的后续计算时间即为常数(给定 时),从而在总计算时间中引入一个 项。因此,该算法计算 个点的结构所需时间为 。常数 和 取决于初始选择的 值。作者进行的模拟表明, 尤其会随 的增大而迅速增加,这符合预期。如果在将点输入算法前先对其进行排序(从而减少长距离最近邻搜索的需求),算法时间应为 ,但在实践中,由此带来的节省通常可忽略不计。
图6展示了该算法在2、3和4维空间中处理不同数量点时的运行时间。Green-Sibson算法处理相同的二维500点数据耗时5.5秒,而作者的算法耗时28秒。由于Green-Sibson算法利用了结构的二维特性,预期其速度更快;对于纯二维情形,作者毫不犹豫地推荐使用Green-Sibson算法而非自己的算法。所有运行均在巴斯大学与布里斯托大学共有的双处理器Honeywell Level 68DPS计算机上进行,操作系统为Multics。
致谢
作者感谢社会科学研究院(Social Science Research Council)提供的资助和研究设施,使其得以在巴斯大学的空间数据研究项目中完成此项工作。同时感谢Robin Sibson教授和Peter Green博士,他们首次向作者介绍了Dirichlet镶嵌,其评论与建议极具价值。
于2014年8月21日从 http://comjnl.oxfordjournals.org/ 下载,来源:马萨诸塞大学Healey图书馆
参考文献
Brown, K. Q. (1979). Voronoi diagrams from convex hulls, Inf. Processing letters, Vol. 9 No. 5, p. 223.
Cohen, J. and Hickey, T. (1979). Two algorithms for determining volumes of convex polyhedra, JACM, Vol. 26 No. 3, p. 401.
Gilbert, E. N. (1962). Random subdivisions of space into crystals, Ann. Math. Stat., Vol. 33, p. 958.
Green, P. J. and Sibson, R. (1978). Computing Dirichlet tessellations in the plane, The Computer Journal, Vol. 21, p. 168.
Green, P. J. and Silverman, B. W. (1979). Constructing the convex hull of a set of points in the plane, The Computer Journal, Vol. 22 No. 3, p. 262.
Lawson, C. L. (1972). Generation of a triangular grid with application to contour plotting, Cal. Tech. JPL Technical memorandum No. 299.
Miles, R. E. (1970). On the homogeneous planar Poisson process, Mathematical Biosciences, Vol. 6, p. 85.
Ropley, B. D. (1977). Modelling spatial patterns, JRSS Ser. B, Vol. 39, p. 172; Discussion, p. 192.
Sibson, R. (1978). Locally equiangular triangulations, The Computer Journal, Vol. 21 No. 3, p. 243.
Sibson, R. (1980). A vector identity for the Dirichlet tessellation, Math. Proc. Camb. Phil. Soc., Vol. 87, p. 151.