TRIMEG-GKX：一种采用分段场对齐有限元方法的电磁回旋动理学粒子程序，用于托卡马克芯部等离子体中微观与宏观不稳定性的研究

卢志新，孟果，Roman Hatzky，Philipp Lauber，Matthias Hoelzl

${}^4$马克斯·普朗克等离子体物理研究所，Boltzmannstr. 2，Garching，85748，德国

摘要

本文介绍了TRIMEG-GKX代码的特点，重点阐述了其相较于其他回旋动理学代码所采用的新颖或不同的方案，特别是面向对象编程、无滤波器/缓冲区处理以及高阶分段场对齐有限元方法的使用。TRIMEG-GKX代码采用粒子-网格（particle-in-cell）方案求解电磁回旋动理学方程，并考虑了多粒子种类效应和剪切阿尔芬物理。混合变量/拉回（mixed-variable/pullback）方案已被实现，以支持电磁研究。该代码通过在计算节点间采用粒子分解和区域克隆的方式进行并行化，取代了传统的区域分解技术。

本文展示了该代码在微观与宏观不稳定性研究中的应用，包括高能粒子驱动的阿尔芬本征模、离子温度梯度模以及动力学气球模。在人为设定及实验重构的平衡位形（如ASDEX Upgrade (AUG)、可变位形托卡马克(TCV)和欧洲联合环(JET)）中均取得了良好的模拟性能。未来基于TRIMEG-C1代码、采用高阶 $C^1$ 有限元方法处理三角网格的边界物理研究，将建立在相同的数值方法基础之上。

关键词：电磁回旋动理学模拟，粒子-网格方法，湍流，阿尔芬模，有限元方法

1. 引言

自回旋动理学模拟模型早期发展以来 [1]，过去几十年中已识别出若干重要的非线性物理现象，例如带状流（zonal flows）的产生 [2] 以及湍流对偏滤器边缘热流的影响 [3]。为提升现代回旋动理学粒子程序的能力，人们开发了多种先进的数值与物理方案，例如噪声抑制方案 [4]、各类电磁方案（如迭代 $p_{\parallel }$ 方案 [5]、混合变量/拉回方案 [6]、隐式方案 [7, 8]、GK-E&B 模型及其实现 [9, 10] 以及守恒方案 [11]）。先进的计算方案与全面的物理模型是现代回旋动理学代码成功预测和解释实验结果及其背后物理机制的关键要素 [12, 13, 14]。此外，人们还开发了新的框架与方法，利用几何粒子-网格方法实现高保真粒子模拟 [15, 16]。

目前已开发出基于结构化网格的回旋动理学代码 TRIMEG-GKX [7, 17, 18, 19] 以及基于非结构化三角网格的 TRIMEG-C0/C1 代码 [20, 21, 22]，用于探索适用于物理研究的各种新方法。自早期采用非结构化网格开发以来 [20]，已陆续实现了多种物理模型与数值方案，例如隐式方案 [7]、全-$f$ 混合变量/拉回方案 [17] 以及分段场对齐有限元方法 [18]，充分展示了这些物理与数值方法在回旋动理学研究中的能力。特别地，研究表明，采用高阶有限元方法可在较低网格分辨率下有效捕捉不稳定性特征 [22]。本文展示了 TRIMEG-GKX 代码（下文简称 GKK）的最新进展。与其他回旋动理学粒子代码相比，GKK 代码具有以下特点：

1. 采用面向对象编程原则，便于引入多种粒子种类及不同的物理模型，例如静电或电磁回旋动理学模型。

2. 采用分段场对齐有限元方法（PFAFEM），并在径向、极向和环向方向上应用三次 B 样条函数。

3. 傅里叶滤波器的使用被最小化，尤其是在三维电磁模型中。取而代之的是，在回旋中心运动方程中采用对强形式（strong form）的严格处理。

4. 粒子推进器的缓存性能经过专门优化，这与其它回旋动理学粒子代码中常用的排序方案有所不同。

5. 采用了粒子分解方法，但由于以下原因，用计算节点间的区域克隆（domain cloning）取代了传统的区域分解（domain decomposition）：(1) 通过 MPI-3 标准利用共享内存，降低了每个计算节点的总内存消耗；(2) 应用了 PFAFEM 方法，使得三维网格在某一维度上的网格点数量可减少约一个数量级；(3) 采用三次 B 样条基函数，因此在环向方向上涉及四个基函数。

本文其余部分组织如下：第 2 节介绍 GKX 代码中实现的模型和方程；第 3 节描述数值方法；第 4 节展示多种情形下的模拟结果，包括人为设定的平衡态和真实的实验位形；最后，第 5 节讨论结论及未来工作的展望。

2. 模型与方程

本文所采用的物理模型与早期关于 pullback 格式的相关工作 [23]、我们先前发展的混合全 $f$-$\delta f$ 格式 [17] 以及其中引用的文献 [4, 6, 12] 密切相关。本文重点研究传统的 $\delta f$ 模型。

2.1. 使用混合变量的物理方程

混合变量定义如下：扰动磁矢势的平行分量 $\delta A_{\parallel }$ 被分解为辛部分（symplectic part）和哈密顿部分（Hamiltonian part）[23]：

$$\delta A_{\parallel }=\delta A_{\parallel }^{\mathrm{s}}+\delta A_{\parallel }^{\mathrm{h}},$$

其中辛部分 $\delta A_{\parallel }^{\mathrm{s}}$ 的选取需满足包含静电标量势 $\delta \Phi$ 的理想欧姆定律，即：

$${\partial }_t\delta A_{\parallel }^{\mathrm{s}}+{\partial }_{\parallel }\delta \Phi =0,$$

其中平行导数定义为 ${\partial }_{\parallel }=\mathbf{b}\cdot \nabla$，$\mathbf{b}=\mathbf{B}/B$，$\mathbf{B}$ 为平衡磁场。回旋中心的平移平行速度坐标 $u_{\parallel }$ 定义为

$$u_{\parallel }=v_{\parallel }+\frac{q_s}{m_s}⟨\delta A_{\parallel }^{\mathrm{h}}⟩,$$

其中 $v_{\parallel }$ 为平行速度，$q_s$ 和 $m_s$ 分别为物种 $s$ 的电荷与质量，下标 “s” 表示不同的粒子种类，$⟨\dots ⟩$ 表示回旋平均。

回旋中心的运动方程与先前的工作 [6, 4, 12, 24, 13] 一致：

$$\begin{array}{rl}{\dot{R}}_0& =u_{\parallel }{b}_0^{\ast }+\frac{m\mu }{q{B}_{\parallel }^{\ast }}b\times \nabla B,\end{array}$$

$$\begin{array}{rlr}{\dot{u}}_{\parallel ,0}& =& -\mu {\mathbf{b}}_0^{\ast }\cdot \nabla B,\end{array}$$

$$\delta \dot{R}=\frac{b}{B_{\parallel }^{\ast }}\times \nabla ⟨\delta \Phi -u_{\parallel }\delta A_{\parallel }⟩-\frac{q_s}{m_s}⟨\delta A_{\parallel }^{\mathrm{h}}⟩b^{\ast },$$

$$\begin{array}{rlr}\delta {\dot{u}}_{\parallel }& =& -\frac{q_s}{m_s}\left({\mathbf{b}}^{\ast }\cdot \nabla ⟨\delta \Phi -u_{\parallel }\delta A_{\parallel }^{\mathrm{h}}⟩+{\partial }_t⟨\delta A_{\parallel }^{\mathrm{s}}⟩\right)\\ & & -\frac{\mu }{B_{\parallel }^{\ast }}\mathbf{b}\times \nabla B\cdot \nabla ⟨\delta A_{\parallel }^{\mathrm{s}}⟩,\end{array}$$

其中磁矩 $\mu =v_{\perp }^2/(2B)$，$b^{\ast }=b_0^{\ast }+\nabla ⟨\delta A_{\parallel }^{\mathrm{s}}⟩\times b/B_{\parallel }^{\ast }$，$⟨\dots ⟩$ 表示回旋平均，$b_0^{\ast }=b+(m_s/q_s)u_{\parallel }\nabla \times b/B_{\parallel }^{\ast }$，$b=B/B$，$B_{\parallel }^{\ast }=B+(m_s/q_s)u_{\parallel }\mathbf{b}\cdot (\nabla \times \mathbf{b})$。注意，在我们之前的工作 [17] 中，右侧采用的是 $v_{\parallel }$，因此 $\dot{\mathbf{R}}$ 中的项 $-(q_s/m_s)⟨\delta A_{\parallel }^{\mathrm{h}}⟩{\mathbf{b}}^{\ast }$ 被计入 ${\dot{\mathbf{R}}}_0$ 中。回旋中心运动方程在 $(r,\varphi ,\theta )$ 坐标系中的表达式列于附录 A。

2.2. 场方程

在长波长近似下，线性化的准中性方程如下：

$$-\nabla \cdot \left(\sum _s\frac{q_s{n}_{0s}}{B{\omega }_{cs}}{\nabla }_{\perp }\delta \Phi \right)=\sum _s{q}_s\delta n_{s,v},$$

其中，回旋中心密度 $\delta n_{s,v}$ 由 $\delta f_s(\mathbf{R},v_{\parallel },\mu )$（记为 $\delta f_{s,v}$）计算得到，即
$$\delta n_{s,v}(\mathbf{x})=\int {\mathrm{d}}^{6}z\delta f_{s,v}\delta (\mathbf{R}+\mathbf{\rho }-\mathbf{x})。$$
此处，$\mathbf{x}$ 和 $\mathbf{R}$ 分别表示粒子坐标和回旋中心坐标，$\mathbf{\rho }$ 表示拉莫尔半径。在式 (8) 中，${\omega }_{\mathrm{cs}}$ 是物种 $s$ 的回旋频率；在本工作中，我们忽略了方程左侧的扰动电子极化密度。当采用 $\delta f$ 方案时，$\delta f_{s,v}$ 可通过 $\delta f_{s,u}$ 并结合拉回（pullback）方案的线性近似得到：

$$\delta f_{s,v}=\delta f_{s,u}+\frac{q_s⟨\delta A_{\parallel }^{\mathrm{h}}⟩}{m_s}\frac{\partial f_{0s}}{\partial v_{\parallel }}\text{（Maxwellian 情形下 }{f}_{0s}=f_{\mathrm{M}}\text{）}-\frac{v_{\parallel }}{T_s}{q}_s⟨\delta A_{\parallel }^{\mathrm{h}}⟩f_{0s},$$

该式由非线性拉回方案的一般形式 [4] 推导而来：

$$f_{s,v}(v_{\parallel })=f_{s,u}\left(v_{\parallel }+\frac{q_s}{m_s}⟨\delta A_{\parallel }^{\mathrm{h}}⟩\right).$$

在 $v_{\parallel }$ 空间中的安培定律为

$$-{\nabla }_{\perp }^2\delta A_{\parallel }={\mu }_0\delta j_{\parallel ,v},$$

其中 $\delta j_{\parallel ,v}(\mathbf{x})={\sum }_s{q}_s\int {\mathrm{d}}^{6}z\delta f_{s,v}\delta (\mathbf{R}+\mathbf{\rho }-\mathbf{x})v_{\parallel }$。

对于 $\delta f$ 模型，采用混合变量并假设麦克斯韦分布，我们有

$$\begin{array}{rl}\delta j_{\parallel ,v}& \equiv {\sum }_s{q}_s\int \mathrm{d}{z}^6{v}_{\parallel }\delta f_{s,v}(v_{\parallel })\delta (R+\rho -x)\\ & ={\sum }_s{q}_s\int \mathrm{d}{z}^6{v}_{\parallel }\left(\delta f_{s,u}(u_{\parallel })-\frac{v_{\parallel }{q}_s⟨\delta A_{\parallel }^{\mathrm{h}}⟩}{T_s}{f}_{0s}\right)\delta (R+\rho -x)\end{array}$$

于是，我们可以将安培定律写为

$$\begin{array}{rl}& -{\nabla }_{\perp }^2\delta A_{\parallel }^{\mathrm{h}}+{\sum }_s{\mu }_0\frac{q_s^2}{T_s}\int \mathrm{d}{z}^6{v}_{\parallel }^2{f}_{0s}⟨\delta A_{\parallel }^{\mathrm{h}}⟩\delta (R+\rho -x)\\ & ={\nabla }_{\perp }^2\delta A_{\parallel }^{\mathrm{s}}+{\mu }_0{\sum }_s{q}_s\int \mathrm{d}{z}^6{v}_{\parallel }\delta f_{s,u}(u_{\parallel })\delta (R+\rho -x).\end{array}$$

左边的积分可以解析求得，结果为

$$\begin{array}{rl}-{\nabla }_{\perp }^2\delta A_{\parallel }^{\mathrm{h}}& +{\sum }_s\frac{1}{d_s^2}⟨\delta A_{\parallel }^{\mathrm{h}}⟩={\nabla }_{\perp }^2\delta A_{\parallel }^{\mathrm{s}}\\ & +{\mu }_0{\sum }_s{q}_s\int \mathrm{d}{z}^6{v}_{\parallel }\delta f_{s,u}(u_{\parallel })\delta (R+\rho -x),\end{array}$$

$$\overline{⟨\delta A_{\parallel }^{\mathrm{h}}⟩}\equiv \frac{2}{n_{s0}{v}_{ts}^2}\int \mathrm{d}{z}^6{v}_{\parallel }^2{f}_{0s}⟨\delta A_{\parallel }^{\mathrm{h}}⟩\delta (R+\rho -x),$$

其中 $v_{\mathrm{ts}}=\sqrt{2T_s/m_s}$，$d_s$ 是物种 $s$ 的趋肤深度，定义为 $d_s^2=c^2/{\omega }_{p,s}^2=m_s/({\mu }_0{q}_s^2{n}_{0s})$，而式 (15) 中的积分未进行解析简化，以便捕捉 $f_0$ 偏离麦克斯韦分布时的数值或物理偏差。

对于完整的 $f$ 模型，扰动电流由完整的 $f$ 表示，

$$\begin{array}{rlr}{\dot{j}}_{\parallel ,v}& =& {\sum }_s{q}_s\int \mathrm{d}{v}^3{v}_{\parallel }{f}_{s,v}\\ & =& {\sum }_s{q}_s\int \mathrm{d}{z}^6\left[u_{\parallel }-\frac{q_s}{m_s}⟨\delta A_{\parallel }^{\mathrm{h}}⟩\right]f_{s,v}\delta (R+\rho -x).\end{array}$$

安培定律给出

$$\begin{array}{rl}& -{\nabla }_{\perp }^2\delta A_{\parallel }^{\mathrm{h}}+{\mu }_0{\sum }_s\frac{q_s^2}{m_s}\int \mathrm{d}{z}^6{f}_{s,v}⟨\delta A_{\parallel }^{\mathrm{h}}⟩\delta (R+\rho -x)\\ & ={\nabla }_{\perp }^2\delta A_{\parallel }^{\mathrm{s}}+{\mu }_0{\sum }_s{q}_s\int \mathrm{d}{z}^6{u}_{\parallel }{f}_{s,v}\delta (R+\rho -x).\end{array}$$

相应的解析极限形式与式 (14) 类似，只是将 $\delta f_{s,u}(u_{\parallel })$ 替换为 $f_{s,v}(v_{\parallel })$，并重新定义 $⟨\delta A_{\parallel }^{\mathrm{h}}⟩$，

$$\begin{array}{rl}-{\nabla }_{\perp }^2\delta A_{\parallel }^{\mathrm{h}}+{\sum }_s\frac{1}{d_s^2}\overline{⟨\delta A_{\parallel }^{\mathrm{h}}⟩}& ={\nabla }_{\perp }^2\delta A_{\parallel }^{\mathrm{s}}\\ & +{\mu }_0{\sum }_s{q}_s\int \mathrm{d}{z}^6{v}_{\parallel }{f}_{s,v}(v_{\parallel })\delta (R+\rho -x)\end{array}$$

其中

$$\overline{⟨\delta A_{\Vert }^{\mathrm{h}}⟩}\equiv \frac{1}{n_{s0}}\int \mathrm{d}{z}^6{f}_{s,v}(v_{\Vert })⟨\delta A_{\Vert }^{\mathrm{h}}⟩\delta (R+\rho -x).$$

对于 $\delta f$ 模型和全 $f$ 模型，采用迭代格式，其渐近解可表示为：

$$\delta A_{\parallel }^{\mathrm{h}}=\sum _{I=0}^{\infty }\delta A_{\parallel ,I}^{\mathrm{h}},$$

其中 $|\delta A_{\parallel ,I+1}^{\mathrm{h}}/\delta A_{\parallel ,I}^{\mathrm{h}}|\ll 1$ 的条件由以下事实保证：解析的趋肤深度项（即方程 (14) 左边第二项）与精确项（即方程 (14) 右边第二项）非常接近。安培定律按阶次逐级求解：

$$\left({\nabla }_{\perp }^2-\sum _s\frac{1}{d_s^2}\right)\delta A_{\Vert ,0}^{\mathrm{h}}=-{\nabla }_{\perp }^2\delta A_{\Vert }^{\mathrm{s}}-{\mu }_0\delta j_{\Vert }.$$

$$\left({\nabla }_{\perp }^2-\sum _s\frac{1}{d_s^2}\right)\delta A_{\Vert ,I}^{\mathrm{h}}=-\sum _s\frac{1}{d_s^2}\delta A_{\Vert ,I-1}^{\mathrm{h}}+\sum _s\frac{1}{d_s^2}\overline{⟨\delta A_{\Vert ,I-1}^{\mathrm{h}}⟩},$$

$$\overline{⟨\delta A_{\parallel ,I-1}^{\mathrm{h}}⟩}=\frac{2}{n_0{v}_{\mathrm{ts}}^2}\int \mathrm{d}{z}^6{v}_{\parallel }^2{f}_{0s}⟨\delta A_{\parallel ,I-1}^{\mathrm{h}}⟩\delta (R+\rho -x)\text{for}\delta f\text{model},(23)$$

$$\overline{⟨\delta A_{\Vert ,I-1}^{\mathrm{h}}⟩}=\frac{1}{n_0}\int \mathrm{d}{z}^6{f}_{s,v}⟨\delta A_{\Vert ,I-1}^{\mathrm{h}}⟩\delta (R+\rho -x)\text{for full }f\text{ model},$$

其中 $I=1,2,3,\dots$。对于麦克斯韦分布，当忽略有限拉莫半径（FLR）效应时——这对电子是合理的，因为电子是趋肤深度项的主要贡献者——我们有 $2/(n_0{v}_{\mathrm{ts}}^2)\int \mathrm{d}{v}^3{v}_{\parallel }^2{f}_0=1$ 以及 $(1/n_0)\int \mathrm{d}{v}^3{f}_0=1$。在此条件下，电子趋肤深度项的解析表达式与精确值非常接近。因此，该迭代求解器预期具有良好的收敛性，从而能够高效且准确地计算趋肤深度的贡献。

2.3. 用于缓解抵消问题的回拉（pullback）方案

关于 $\delta f$ 方法的回拉方案的更详细描述可参见先前的工作 [6]，以及全 $f$ 和混合全 $f$-$\delta f$ 方法的回拉方案 [17]。作为简要回顾，$\delta f$ 的相关方程如下所示：

$$\delta A_{\parallel ,\mathrm{new}}^{\mathrm{s}}=\delta A_{\parallel ,\mathrm{old}}^{\mathrm{s}}+\delta A_{\parallel ,\mathrm{old}}^{\mathrm{h}},$$

$$u_{\parallel ,\mathrm{new}}=u_{\parallel ,\mathrm{old}}-\frac{q_s}{m_s}⟨\delta A_{\parallel ,\mathrm{old}}^{\mathrm{h}}⟩,$$

$$\delta f_{\mathrm{new}}=\delta f_{\mathrm{old}}+\frac{q_s⟨\delta A_{\parallel ,\mathrm{old}}^{\mathrm{h}}⟩}{m_s}\frac{\partial f_{0s}}{\partial v_{\parallel }}{|}_{f_{0s}=f_M}\delta f_{\mathrm{old}}-\frac{2v_{\parallel }}{v_{\mathrm{ts}}^2}\frac{q_s⟨\delta A_{\parallel ,\mathrm{old}}^{\mathrm{h}}⟩}{m_s}{f}_{0s},$$

其中下标为“new”和“old”的变量分别表示拉回变换之后和之前的量。式（27）是 $\delta f$ 的线性化方程，

该拉回变换来自于分布函数变换的一般方程：

$$f_{\mathrm{old}}(u_{\parallel ,\mathrm{old}})=f_{\mathrm{new}}\left(u_{\parallel ,\mathrm{new}}=u_{\parallel ,\mathrm{old}}-\frac{q_s}{m_s}⟨\delta A_{\parallel ,\mathrm{old}}^{\mathrm{h}}⟩\right)$$

对于完整的 $f$ 方案，仅需式（25）和（26）。

2.4. 分布函数的离散化

采用粒子模拟方案，使用 $N$ 个标记粒子来近似给定的分布：

$$g(z,t)\approx \sum _{p=1}^N\frac{\delta [z_p-z_p(t)]}{J_z},$$

其中 $z$ 是相空间坐标，$\delta$ 是狄拉克δ函数，$J_z$ 是相应的雅可比行列式，本文采用的相空间坐标为 $z=(\mathbf{R},v_{\parallel },\mu )$，其中 $\mu$ 为磁矩，$v_{\parallel }$ 为平行速度，$\mathbf{R}$ 为实空间坐标。粒子的总分布由这些标记粒子表示为：

$$f(z,t)=C_{g2f}{P}_{\mathrm{tot}}(z,t)g(z,t)\approx C_{g2f}\sum _{p=1}^N{p}_{p,\mathrm{tot}}(t)\frac{\delta [z_p-z_p(t)]}{J_z},$$

其中常数 $C_{g2f}\equiv N_f/N_g$，$N_{f/g}$ 分别为物理粒子数与标记粒子数，$g$ 和 $f$ 分别指代标记粒子和物理粒子。对于无碰撞等离子体，

$$\frac{\mathrm{d}g(z,t)}{\mathrm{d}t}=0,\frac{\mathrm{d}f(z,t)}{\mathrm{d}t}=0.$$

对于每个标记粒子，

$$p_{p,\mathrm{tot}}(t)=\frac{1}{C_{g2f}}\frac{f(z_p,t)}{g(z_p,t)}=\frac{N_g}{N_f}\frac{n_f}{n_g}\frac{f_v(z_p,t)}{g_v(z_p,t)}=\frac{n_f}{⟨n_f{⟩}_V}\frac{⟨n_g{⟩}_V}{n_g}\frac{f_v(z_p,t)}{g_v(z_p,t)},$$

其中 $n_f$ 是密度分布，$f_v$ 是速度空间中的分布，即粒子分布函数可表示为 $f=n_f(\mathbf{R})f_v(v_{\parallel },\mu )$，$⟨\dots {⟩}_V$ 表示体积平均。如前所述 [4, 12]，标记粒子的分布函数有多种选择。在本工作中，标记粒子在环向方向和 $(R,Z)$ 平面上随机初始化并均匀分布，其速度空间分布与物理粒子相同，从而得到

$$p_{p,\mathrm{tot}}(z,t)=\frac{{\varphi }_{\mathrm{wid}}SR}{V_{\mathrm{tot}}},$$

其中 ${\varphi }_{\mathrm{wid}}$ 是模拟区域在环向方向的宽度，$S$ 是极向截面的面积，$V_{\mathrm{tot}}$ 是总体积。对于具有同心圆磁面的托卡马克平衡态，式 (33) 可简化为 $p_{p,\mathrm{tot}}(z,t)=n_{f}R/(⟨n_f{⟩}_V{R}_0)$。

对于 $\delta f$ 模型，总分布函数被分解为背景部分和扰动部分，即 $f(z,t)=f_0(z,t)+\delta f(z,t)$。背景部分可选为不随时间变化的形式，即 $f_0(z,t)=f_0(z)$，典型的选择是局域麦克斯韦分布。背景分布函数和扰动分布函数通过标记粒子表示如下：

$$f_0(z,t)=P(z,t)g(z,t)\approx \sum _{p=1}^N{p}_p(t)\frac{\delta [z_p-z_p(t)]}{J_z},$$

$$\delta f(z,t)=W(z,t)g(z,t)\approx \sum _{p=1}^N{w}_p(t)\frac{\delta \left[z_p-z_p(t)\right]}{J_z},$$

其中 $p_p(t)=f_0(z_p,t)/g(z_p,t)=P(z_p,t)$ 和 $w_p(t)=\delta f(z_p,t)/g(z_p,t)=W(z_p,t)$ 是随时间变化的变量。

2.5. 分布函数的演化

分布函数的演化由标记粒子的权重 $w_p$ 和 $p_p$ 的演化来表示。其演化方程可直接得出 [12]：

$${\dot{w}}_p(t)=-p_p(t)\frac{\mathrm{d}}{\mathrm{d}t}\left[\ln f_0(z_p(t))\right],$$

$${\dot{p}}_p(t)=p_p(t)\frac{\mathrm{d}}{\mathrm{d}t}\left[\ln f_0(z_p(t))\right],$$

$$\frac{\mathrm{d}}{\mathrm{d}t}=\frac{\partial }{\partial t}+\dot{R}\cdot \nabla +{\dot{v}}_{\parallel }\frac{\partial }{\partial v_{\parallel }},$$

其中在最后一个方程中假设磁矩为常数，即 $\dot{\mu }=0$。通常，回旋中心的运动方程可分解为与平衡磁场相关的平衡部分和与扰动场相关的扰动部分：

$$\dot{R}={\dot{R}}_0+\delta \dot{R},$$

$${\dot{v}}_{\parallel }={\dot{v}}_{\parallel ,0}+\delta {\dot{v}}_{\parallel }.$$

时间导数定义为：

$$\frac{\mathrm{d}}{\mathrm{d}t}={\frac{\mathrm{d}}{\mathrm{d}t}|}_0+{\frac{\mathrm{d}}{\mathrm{d}t}|}_1,$$

$${\frac{\mathrm{d}}{\mathrm{d}t}|}_0=\frac{\partial }{\partial t}+{\dot{R}}_0\cdot \nabla +{\dot{v}}_{\parallel ,0}\frac{\partial }{\partial v_{\parallel }},$$

$${\frac{\mathrm{d}}{\mathrm{d}t}|}_1=\delta \dot{R}\cdot \nabla +\delta {\dot{v}}_{\parallel }\frac{\partial }{\partial v_{\parallel }}.$$

对于平衡分布函数，

$${\frac{\mathrm{d}}{\mathrm{d}t}|}_0{f}_0=0,$$

因此有

$$\frac{\mathrm{d}}{\mathrm{d}t}{f}_0={\frac{\mathrm{d}}{\mathrm{d}t}|}_1{f}_0,$$

其中 $f_0$ 被选为定态解（$\partial f_0/\partial t=0$）。在本文中，选择局域麦克斯韦分布（$f_0=f_{\mathrm{M}}$）：

$$f_{\mathrm{M}}=\frac{n_0}{(2T/m{)}^{3/2}{\pi }^{3/2}}\exp \left(-\frac{m{v}_{\parallel }^2}{2T}-\frac{m\mu B}{T}\right),$$

满足 $\int f_{\mathrm{M}}{J}_{v}d{\nu }_{\parallel }d\mu =n_0$，其中 $J_v=2\pi B$。因此，

$$\frac{\mathrm{d}}{\mathrm{d}t}\ln f_{\mathrm{M}}=\delta \dot{\mathbf{R}}\cdot \left[{\vec{\kappa }}_n+\left(\frac{m{v}_{\parallel }^2}{2T}+\frac{m\mu B}{T}-\frac{3}{2}\right){\vec{\kappa }}_T-\frac{m\mu B}{T}{\vec{\kappa }}_B\right]-\delta {\dot{v}}_{\parallel }\frac{m{v}_{\parallel }}{T},$$

其中 ${\vec{\kappa }}_{n,T,B}\equiv \nabla \ln \{n,T,B\}$。需要注意的是，对于局域麦克斯韦分布，本文在 $\delta f$ 方案中采用了如下近似：假设 $\mathrm{d}{f}_{\mathrm{M}}/\mathrm{d}t{|}_0=0$，以消除新经典驱动项。

3. 数值方法

3.1. 基于面向对象编程的代码结构

GKK 代码基于结构化网格，用于研究托卡马克装置中的芯部等离子体 [7, 17]。该代码使用 Fortran 编写，并采用了面向对象编程（OOP）原则，其结构类似于基于非结构化网格的 TRIMEG-C0/C1 代码 [20, 22]。回旋动理学场-粒子系统被分解为不同的类，即平衡类、粒子类、场类、求解器类和 B 样条类。回旋动理学场-粒子类的应用由其他基础类构建而成。Fortran 代码的核心部分约有 20,000 行。线性场方程的求解采用 PETSc 库中的 KSP 求解器。利用 MPI3 标准中的共享内存特性来存储三维场量，以确保高效的内存使用。平衡变量采用 B 样条表示 [25]。有限元方法（FEM）使用三次 B 样条实现，具体细节见我们之前的工作 [17]。

代码的结构如图1所示。三个物理类分别为平衡类（equilibrium）、场类（field）和粒子类（particle）。其他类，例如求解器类（solver）、样条类（spline）和gkem2sp类，主要用于数值方法和物理应用。这些类的简要描述如下：

1. 平衡类（equilibrium）处理解析和数值（EQDSK）平衡，并向其他类提供平衡数据。

2. 粒子类（particle）求解回旋中心运动方程、处理权重方程，并执行投影操作（“散射”）。
   场类（field）定义场方程，并利用样条类（spline）和求解器类（solver）求解场方程。它还通过样条类进行插值，向粒子提供场量（“收集”）。
   粒子坐标类（particle coordinate）在时间积分器中用于存储中间信息。

3. 求解器类（solver）负责矩阵的存储以及线性方程组的求解过程。

4. 三维三次样条类（3D cubic spline）提供与三维B样条有限元方法相关的变量和算法。

5. 回旋动理学电磁类（gyrokinetic electromagnetic）包含一个平衡类实例、一个场类实例，以及一个粒子类实例数组（以支持多种粒子种类）。

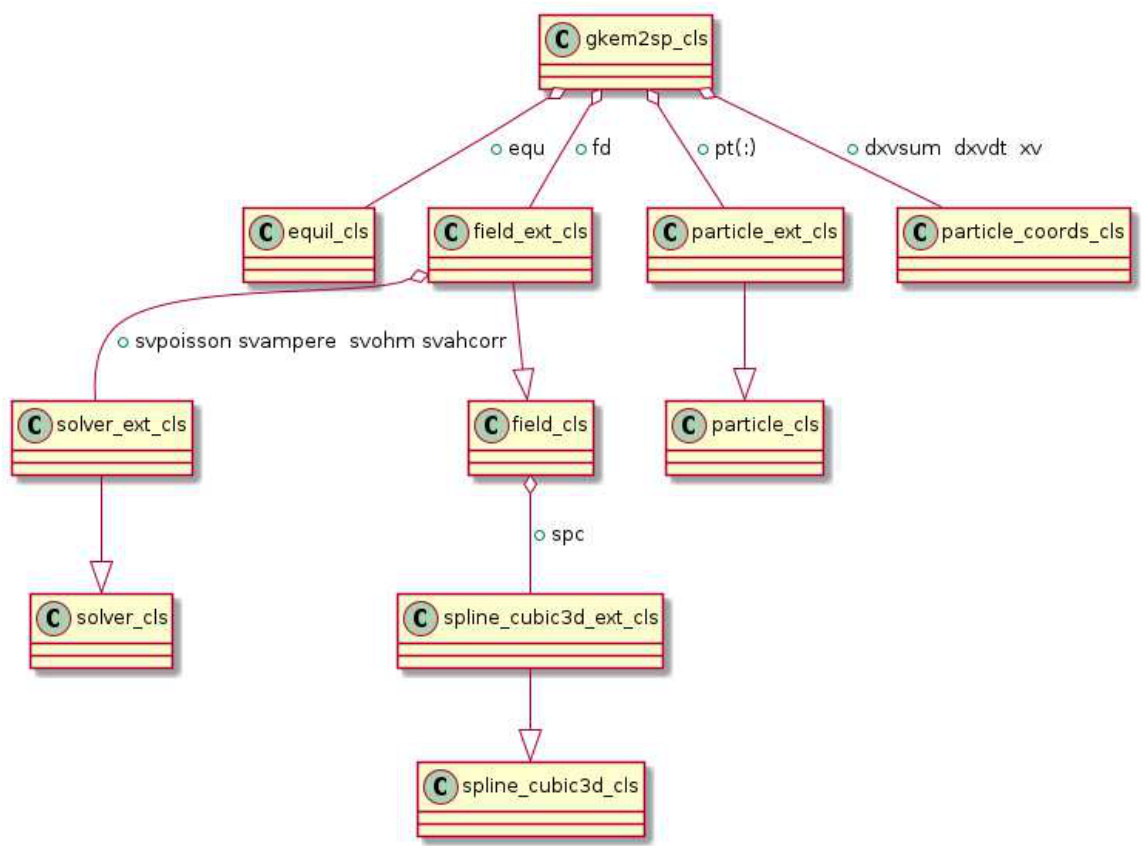
图1：GKK代码的UML（统一建模语言）图。

3.2 归一化

本节描述TRIMEG-GKK代码中变量的归一化方法。归一化所用的单位以下标“N”表示。归一化的参考长度为 $R_{\mathrm{N}}=1$ $\mathbf{m}$，因为该代码不仅旨在研究微观不稳定性，还关注测地声模等大尺度模结构。此外，采用 $R_{\mathrm{N}}=1$ $\mathbf{m}$ 可直接使用平衡（EQDSK）文件中的空间坐标，无需额外归一化。粒子质量归一化为 $m_{\mathrm{N}}$，其中 $m_{\mathrm{N}}=m_{\mathrm{p}}$（质子质量）。速度单位定义为 $v_{\mathrm{N}}\equiv \sqrt{2T_{\mathrm{N}}/m_{\mathrm{N}}}$，其中 $T_{\mathrm{N}}$ 和 $m_{\mathrm{N}}$ 分别为归一化所用的参考温度和质量。在TRIMEG代码中，通常选择某一指定径向位置处的电子温度作为 $T_{\mathrm{N}}$，并取质子质量作为 $m_{\mathrm{N}}$。时间单位则为 $t_{\mathrm{N}}=R_{\mathrm{N}}/v_{\mathrm{N}}$。电荷单位为基本电荷 $e$。温度以 $T_{\mathrm{N}}$ 归一化。磁矩 $\mu$ 以 $v_{\mathrm{N}}^2/B_{\mathrm{N}}$ 归一化，本文中取 $B_{\mathrm{N}}=1$ T，以便直接使用EQDSK文件中的磁场数据而无需额外归一化。

除了上述归一化单位外，还引入了两个参考量：参考密度 $n_{\mathrm{ref}}$ 和参考磁场 $B_{\mathrm{ref}}$。这两个量用于定义两个基本参数：参考等离子体贝塔值 ${\beta }_{\mathrm{ref}}$ 和参考拉莫尔半径 ${\rho }_{\mathrm{ref}}$，其表达式为

$${\beta }_{\mathrm{ref}}=\frac{{\mu }_0{n}_{\mathrm{ref}}{m}_{\mathrm{N}}{v}_{\mathrm{N}}^2}{B_{\mathrm{ref}}^2},{\rho }_{\mathrm{ref}}=\frac{m_{\mathrm{N}}{v}_{\mathrm{N}}}{e{B}_{\mathrm{ref}}},$$

其中，${\beta }_{\mathrm{ref}}$ 出现在归一化的安培定律中，而 ${\rho }_{\mathrm{ref}}$ 出现在归一化的回旋中心运动方程中。${\beta }_{\mathrm{ref}}$ 表征电磁效应的强度，而 $a/{\rho }_{\mathrm{ref}}$ 表示归一化的装置尺寸，其中 $a$ 为装置的小半径。需要注意的是，TRIMEG 中采用的归一化方式与其他回旋动理学代码（如 ORB5 [12] 和 EUTERPE [13]）所采用的方式不同。特别地，由于 TRIMEG 中平衡重构基于 EQDSK 文件，而 EQDSK 文件使用的长度单位为 $R_N=1\mathrm{m}$，因此该长度被选作长度单位。同时，${\rho }_{\mathrm{ref}}$ 仍作为一个辅助变量保留下来，因为它在与磁漂移速度和有限拉莫尔半径效应相关的表达式中具有明确的物理意义。

3.3 分段场对齐有限元方法

分段场对齐有限元方法（PFAFEM）已在我们之前的工作中提出，并已应用于静电粒子模拟 [18]。在本工作中，PFAFEM 已被扩展并应用于电磁模型。该方法具有两个关键特征：

1. 计算网格采用传统排布方式，无需任何偏移。
2. 有限元基函数定义在分段场对齐坐标上，每个基函数沿磁力线方向保持连续。

PFAFEM 的基本思想总结如下 [18]。我们从托卡马克坐标 $(r,\varphi ,\theta )$ 出发，其中 $r$、$\varphi$ 和 $\theta$ 分别为类径向、类环向和类极向坐标。安全因子定义为 $q(r,\theta )\equiv \mathbf{B}\cdot \nabla \varphi /(\mathbf{B}\cdot \nabla \theta )$。在每个以 ${\varphi }_k$ 网格为中心的环向子区域中，定义局部的分段场对齐坐标 ${\eta }_k$ 如下：

$${\eta }_k(r,\theta ,\varphi )=\theta -{\int }_{{\varphi }_k}^{\varphi }\mathrm{d}{\varphi }^{\prime }\frac{1}{q(r,{\theta }^{\prime }(r,{\varphi }^{\prime }),{\varphi }^{\prime })},$$

其中积分路径沿磁力线进行，安全因子 $q=q(r,{\theta }^{\prime },{\varphi }^{\prime })$，而 ${\theta }^{\prime }$ 由沿磁力线变化 ${\varphi }^{\prime }$ 所确定，即满足 $d{\theta }^{\prime }/d{\varphi }^{\prime }=1/q(r,{\theta }^{\prime },{\varphi }^{\prime })$；${\varphi }_k$ 和 $\varphi$ 分别表示积分的起点和终点。对于直磁力线坐标 $r,\bar{\theta },\bar{\varphi }$，有

$${\eta }_k(r,\bar{\theta },\bar{\varphi })=\bar{\theta }-\frac{\bar{\varphi }-{\bar{\varphi }}_k}{q},$$

其中安全因子 $\bar{q}=\bar{q}(r)$。分段场对齐有限元基函数定义在 $(r,\varphi ,{\eta }_k)$ 坐标系中。粒子位置处的场插值（“收集”）、扰动密度和平行电流的计算（“散射”）均可在 $(r,\varphi ,{\eta }_k)$ 坐标系中完成。此外，场方程的矩阵也在 $(r,\varphi ,{\eta }_k)$ 坐标系中计算。PFAFEM 与托卡马克等离子体中波包的理论研究一致 [26]。可以证明，PFAFEM 满足单位分解（partition of unity）性质。更多细节可参见我们之前的工作 [18]。

3.4 三维场对齐有限元求解器与混合二维一傅里叶求解器

本工作开发了两种求解器以处理不同类型的问题：一种是混合粒子-单元-粒子-傅里叶（PIC-PIF）求解器，在径向和极向采用有限元方法，而在环向采用傅里叶表示（称为 2D1F 方法）[17]；另一种是三维场对齐有限元方法（FEM）求解器。在 2D1F 求解器中，$(r,\theta )$ 方向采用有限元方法（FEM），而环向 $(\varphi )$ 方向采用粒子-傅里叶（PIF）方案。相比之下，三维求解器在所有三个空间方向均采用有限元方法。网格尺寸为 $(N_r,N_{\theta },N_{\varphi })$，并采用 $(N_{r,\mathrm{FEM}},N_{\theta ,\mathrm{FEM}},N_{\varphi ,\mathrm{FEM}})$ 个基函数来表示模拟区域中的函数，其中 $N_{r,\mathrm{FEM}}=N_r+\Delta N$，$N_{\theta ,\mathrm{FEM}}=N_{\theta }$，$N_{\varphi ,\mathrm{FEM}}=N_{\varphi }$；当采用三次样条时，$\Delta N=2$。此配置确保了与所施加边界条件的一致性。我们在 $(\theta ,\varphi )$ 方向应用周期性边界条件，在 $r$ 方向实施狄利克雷（Dirichlet）边界条件。所用基函数与我们之前工作 [18] 中的相同。

GKK 代码中求解四个场方程：准中性方程、安培定律、迭代安培方程和欧姆定律。场方程的一般形式为

$$M_L\cdot y=b+M_R\cdot c,$$

其中 $M_L$ 和 $M_R$ 为偏微分算子，$b$ 和 $c$ 为已知向量，$y$ 为待求解的向量。相应地，场方程的一般矩阵形式为

$${\overline{\stackrel{ˉ}{M}}}_{L,i{i}^{\prime },j{j}^{\prime },k{k}^{\prime }}\cdot Y_{i^{\prime }{j}^{\prime }{k}^{\prime }}=B^{i,j,k}+{\overline{\stackrel{ˉ}{M}}}_{R,i{i}^{\prime },j{j}^{\prime },k{k}^{\prime }}\cdot C_{i^{\prime }{j}^{\prime }{k}^{\prime }},$$

其中 $Y_{i^{\prime }{j}^{\prime }{k}^{\prime }}$ 是由线性求解器求解的场变量，$B^{i,j,k}$ 来自通过投影算子处理的标记粒子（markers），$C_{i^{\prime }{j}^{\prime }{k}^{\prime }}$ 是已知的场变量，${\overline{\stackrel{ˉ}{M}}}_{L,i{i}^{\prime },j{j}^{\prime },k{k}^{\prime }}$ 和 ${\overline{\stackrel{ˉ}{M}}}_{R,i{i}^{\prime },j{j}^{\prime },k{k}^{\prime }}$ 分别为方程左右两侧的矩阵。

对于三维场对齐有限元法（FEM）求解器，

$$\begin{array}{rl}{\overline{\stackrel{ˉ}{M}}}_{L/R,i{i}^{\prime },j{j}^{\prime },k{k}^{\prime }}& =\int \mathrm{d}r\mathrm{d}\theta \mathrm{d}\varphi J{N}_{ijk}{M}_{L/R}{N}_{i^{\prime }{j}^{\prime }{k}^{\prime }},\end{array}$$

$$\begin{array}{rl}{B}^{i,j,k}& ={\sum }_s{C}_{p2g,s}{\sum }_{p=1}^{N_g}{w}_p{V}_p{\tilde{N}}_{ijk}(r_p,{\eta }_{p,k},{\varphi }_p),\end{array}$$

其中 ${\tilde{N}}_{ijk}(r,\eta ,\varphi )=N_i(r)N_j({\eta }_k)N_k(\varphi )$，投影算子中的转换因子为 $C_{p2g,s}=-{\bar{q}}_s⟨n{⟩}_V{V}_{\mathrm{tot}}/N_g$，$⟨\dots {⟩}_V$ 表示体积平均，$V_{\mathrm{tot}}$ 为总体积，$V_p$ 是速度的函数（对于准中性方程，$V_p=1$；对于安培定律，$V_p=v_{\parallel }$）。

对于二维一维傅里叶（2D1F）求解器，有

$$\begin{array}{rl}{\overline{\stackrel{ˉ}{M}}}_{L/R,i{i}^{\prime },j{j}^{\prime },k{k}^{\prime }}& =\int \mathrm{d}r\mathrm{d}\theta \mathrm{d}\varphi J{N}_i{N}_j{\mathrm{e}}^{\mathrm{i}k\varphi }{M}_{L/R}(N_i,N_j,{\mathrm{e}}^{-\mathrm{i}k\varphi }){\delta }_{k,-k^{\prime }}\end{array}$$

$$B^{i,j,k}=\sum _s{C}_{p2g,s}\sum _{p=1}^{N_g}{w}_p{V}_p{N}_i(r_p)N_j({\theta }_p){\mathrm{e}}^{-\mathrm{i}k{\varphi }_p},$$

其中 $N_i=N_i(r)$，$N_j=N_j(\theta )$，当 $i=j$ 时 ${\delta }_{i,j}=1$，当 $i\ne j$ 时 ${\delta }_{i,j}=0$，而 $V_p$ 与式 (54) 中的相同。网格变量 $Y_{ijk}$ 和 $B^{ijk}$ 通过“散射”（scatter）和“收集”（gather）过程与粒子相互作用。“散射”操作将电荷密度和电流密度分配回网格；“收集”操作则在粒子位置对场量进行插值。在使用三维场对齐有限元法（3D field-aligned FEM）的散射过程中，基函数 $N_{ijk}(r,\eta ,\varphi )$ 的值在粒子位置处计算，但采用的是 $(r,\eta ,\varphi )$ 坐标，如式 (54) 所示。因此，网格值 $Y^{ijk}$ 是通过对所有使得 $N_{ijk}(r,\eta ,\varphi )$ 非零的粒子求和得到的。

在使用三维场对齐有限元法的收集过程中，粒子位置处的场为：

$$Y(r_p,{\theta }_p,{\varphi }_p)=\sum _{i,j,k}{Y}_{i,j,k}{N}_i(r_p)N_j({\eta }_{k,p})N_k({\varphi }_p).$$

在 TRIMEG 代码中，$\eta (r,\theta ,\varphi )$ 的 B 样条系数存储在一个三维矩阵中，因为当使用 $R,\varphi ,Z$ 坐标时，该方法也适用于开放磁力线区域，并且在“收集”和“散射”过程中均需进行三维插值。作为未来针对使用数值平衡态的核心等离子体模拟的一项优化，$\eta$ 可简化为直场线坐标 $(r,\varphi ,\bar{\theta })$ 下的 $\eta =\bar{\theta }-\varphi /\bar{q}$，其中 $\bar{q}\equiv \mathbf{B}\cdot \nabla \varphi /\mathbf{B}\cdot \nabla \bar{\theta }$ 与 $\bar{\theta }$ 无关，这样只需对 $\bar{q}(r_p)$ 进行一维插值，效率更高。

3.5. 与实验数据结构的接口

GKX 直接与 EQDSK 平衡文件接口，该文件定义了极向磁通 $\psi$ 作为 $(R,Z)$ 的函数。在 GKK 内部，磁场平衡态 $\mathbf{B}$ 通过样条插值重构。对于实验 EQDSK 数据，GKK 采用归一化极向磁通的平方根作为径向坐标，即 $r=\sqrt{(\psi -{\psi }_{\mathrm{axis}})/({\psi }_{\mathrm{edge}}-{\psi }_{\mathrm{axis}})}$。对于具有同心圆形截面的假设平衡态，GKK 采用解析的 $q$ 剖面，并以 $\rho =\sqrt{(R-R_0{)}^2+(Z-Z_0{)}^2}$ 作为径向坐标，因为这种方式更为高效。密度和温度剖面可直接在此坐标系下提供；若以其他坐标（例如实空间坐标或基于环向磁通的坐标）给出，代码可利用平衡数据将其转换为所需形式。

GKX 提供了与 IMAS（Integrated Modelling & Analysis Suite，集成建模与分析套件）数据框架的接口。IMAS 是为 ITER 开发的，采用环向磁通坐标系，包含一套完整的基础设施组件、物理模块和分析工具。在 IMAS 中，数据被组织为“数据条目”（Data Entries），每个数据条目代表一组接口数据结构（IDSs），这些结构组合形成一个统一的数据集。

为便于模拟，GKK 包含从各类 IDS 中提取数据并将其转换为代码所需标准输入格式的脚本。例如，第 4.1 节中的 JET 多离子种类回旋动理学案例即通过此数据处理流程初始化。平衡态 IDS 按照 COCOS = 17 坐标约定 [27] 描述磁平衡信息，并可通过 CHEASE 代码 [28] 转换为 EQDSK 文件格式。

不同时间片的密度和温度数据存储在 coreProfiles IDS 中，表示为环向磁通坐标的函数的一维数组。为将这些剖面表示为极向磁通的函数，需计算环向与极向磁通面之间的映射关系。利用该映射，通过三次插值对剖面进行插值，并重新表示为归一化磁通坐标的函数，即 $r=\sqrt{(\psi -{\psi }_{\text{axis}})/({\psi }_{\text{edge}}-{\psi }_{\text{axis}})}$。更一般地，平行速度和径向电场的剖面也可按同样方式提取和处理。这些物理量将在 GKX 的未来发展中被纳入，以支持在模拟框架中包含新经典物理效应。

3.6. ${\partial }_t\delta A_{\parallel }^{\mathrm{s}}+{\partial }_{\parallel }\delta \Phi$ 的强形式以严格处理回旋中心运动

在 PIC 模拟中，噪声抑制至关重要。根据理想欧姆定律（式 (2)），理论上回旋中心运动方程中的项 ${\partial }_{\parallel }\delta \Phi +{\partial }_t\delta A_{\parallel }^{\mathrm{s}}$ 应为零。然而，在数值上，式 (52) 中分别求解了 $\delta \Phi$ 和 ${\partial }_t\delta A^{\mathrm{s}}$ 的基函数系数，仅满足 ${\partial }_{\parallel }\delta \Phi +{\partial }_t\delta A_{\parallel }^{\mathrm{s}}=0$ 的弱形式。由于有限元表示中固有的近似，在任意位置处 ${\partial }_{\parallel }\delta \Phi +{\partial }_t\delta A_{\parallel }^{\mathrm{s}}$ 并非严格为零，而是具有有限值。在推进回旋中心时，若不加修正，误差会在 $\delta {\dot{u}}_{\parallel }=(e_s/m_s)⟨{\partial }_{\parallel }\delta \Phi +{\partial }_t\delta A_{\parallel }^{\mathrm{s}}⟩+\dots =\sigma +\dots$ 中累积，其中 $\sigma$ 表示粒子位置处的有限数值误差。为提高精度，GKX 并未显式强制 ${\partial }_{\parallel }\delta \Phi +{\partial }_t\delta A_{\parallel }^{\mathrm{s}}=0$ 的条件，而是将 ${\partial }_{\parallel }\delta \Phi$ 和 ${\partial }_t\delta A_{\parallel }^{\mathrm{s}}$ 在公式中分别保留。因此，在回旋中心运动方程中，我们直接使用 ${\partial }_{\parallel }\delta \Phi$ 和 ${\partial }_t\delta A_{\parallel }^{\mathrm{s}}$ 的数值表达式，而不依赖于它们的解析抵消，其形式如下：

$$\delta \Phi (r,\varphi ,\theta )=\sum _{i,j,k}\delta {\Phi }_{i,j,k}{N}_i(r)N_j(\theta )N_k(\varphi ),$$

$$\begin{array}{rlr}{\partial }_t\delta A_{\Vert }^{\mathrm{s}}(R,\varphi ,Z)& =& {\sum }_{i,j,k}({\partial }_t\delta A_{\Vert }^{\mathrm{s}}{)}_{i,j,k}{N}_i(r)N_j(\theta )N_k(\varphi ).\end{array}$$

这被称为采用强形式（strong form），其中 ${\partial }_{\parallel }\delta \Phi$ 和 ${\partial }_t\delta A_{\parallel }^{\mathrm{s}}$ 均被显式地数值表示和计算。系数 $\delta {\Phi }_{i,j,k}$ 来源于准中性方程的弱形式，而 $({\partial }_t\delta A_{\parallel }^{\mathrm{s}}{)}_{i,j,k}$ 则直接来自欧姆定律的弱形式。这种方法能够实现更稳健且精确的模拟，尤其是在未采用傅里叶滤波等降噪技巧的情况下。由于我们避免在模拟边界附近使用数值缓冲区或傅里叶滤波器，这种严格处理方式即使在不使用滤波器或缓冲区的情况下，也能提高计算精度和信噪比。

3.7. 粒子推进器的缓存优化

缓存优化对性能有显著影响。可通过多种方法改善缓存访问效率，例如粒子排序以及粒子/场数据布局的优化。在 GKX 代码中，计算量最大的部分是粒子推进器。在粒子循环中，粒子被逐个推进，在推进每个粒子之前，需在循环内部计算平衡场和扰动场。该过程可用以下伪代码描述：

do i = 1, nptot
    pt_radius = particle%radius(i)
    pt_theta  = particle%theta(i)
    pt_phi    = particle%phi(i)
    pt_Apar   = field%calc_field('apar', pt_radius, pt_theta, pt_phi)
    pt_Phi    = field%calc_field('phi', pt_radius, pt_theta, pt_phi)

pt_B = equ%calc_B(pt_Radius%pt_theta)

particle%onestep(pt_Radius%pt_theta, pt_phi, pt_Apar, pt_Phi, pt_B)

enddo

值得注意的是，在 GKK 代码中，还需要计算额外的场量导数，例如 ${\partial }_{\alpha }\delta \Phi$、${\partial }_{\alpha }\delta A_{\parallel }^{\mathrm{s}}$ 和 ${\partial }_{\alpha }\delta A_{\parallel }^{\mathrm{h}}$，其中 $\alpha \in (r,\theta ,\varphi )$。通过将扰动场的计算移出粒子循环，实现了优化。

do i = 1, nptot

    pt_Apar1d(i) = field%calc_field( &
        field%apar, particle%radius(i), particle%theta(i), particle%phi(i))

enddo

do i = 1, nptot

    pt_Phi1d(i) = field%calc_field( &
        field%phi, particle%radius(i), particle%theta(i), particle%phi(i))

enddo

do i=1,nptot

pt_Radius = particle%radius(i)

pt_theta = particle%theta(i)

pt_phi = particle%phi(i)

pt_Apar = pt_Apar(i)

pt_Phi = pt_Phi(i)

pt_B = equ%calc_B(pt_Radius, pt_theta)

particle%onestep(pt_Radius, pt_theta, pt_Phi, pt_Apar, pt_Phi, pt_B)

enddo

缓存优化对加速效果的影响取决于模拟参数，例如场求解器的类型、标记粒子数量以及网格尺寸。第4.6节采用的典型单谐波模拟包含 $16\times 10^6$ 个电子、$10^6$ 个离子（采用4点回旋平均），以及径向和极向网格分辨率分别为 $N_r=96$、$N_{\theta }=128$。启用和未启用缓存优化时，运行200步所需时间分别为292.5秒和3921.3秒，整体加速比达到13.4。图2展示了该优化带来的各项加速细节。缓存优化不仅加速了粒子推进（pusher）和散射（g2p）操作，还加速了记录（recording）和拉回（pullback）子程序，因为在这些子程序中也需要计算电磁场。

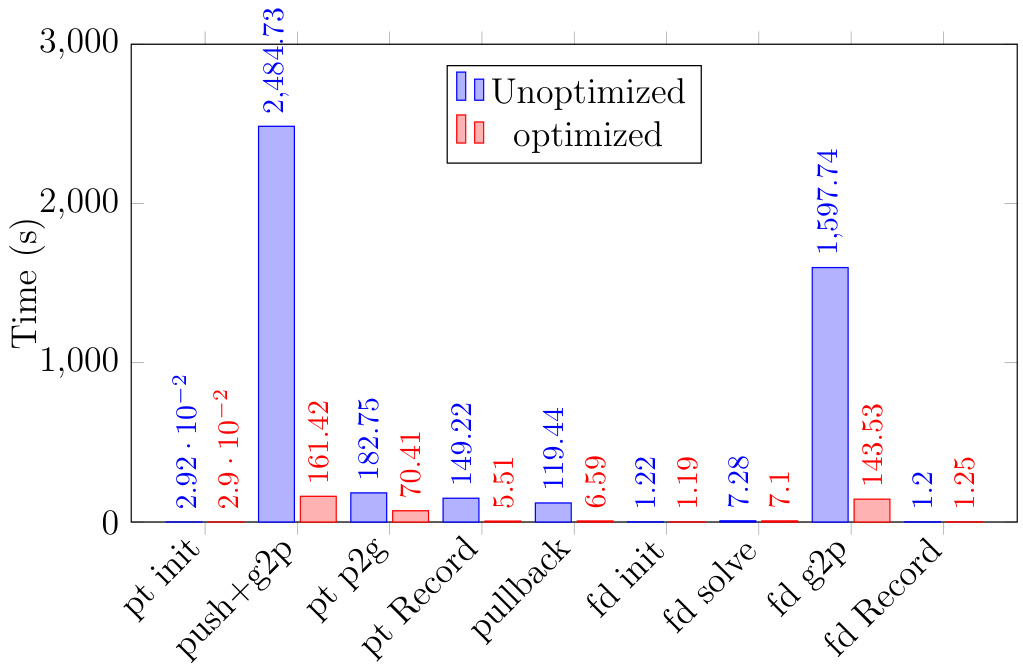
图2：粒子子程序（PT）与场子程序（FD）执行时间对比。 PT时间对两种粒子种类进行了累加。启用和未启用缓存优化时，运行200步所需时间分别为292.5秒和3921.3秒。“g2p”表示场插值（gathering），“p2g”表示散射操作。注意，“g2p”在“push”中被频繁调用，因此将“push+g2p”作为一个整体项列出。

4. 模拟结果

本节展示了我们代码在求解电磁问题方面的高效性。首次将面向对象编程、分段场对齐有限元方法（PFAFEM）、缓存优化以及对 $\delta {\dot{u}}_{\parallel }$ 强形式的严格处理集成到单一代码框架中，以实现高性能计算。TRIMEG-GKX/C0 代码此前的物理应用可参见文献 [29, 21]。迭代安培求解器的收敛性、静电多-$n$ 非线性模拟以及采用傅里叶滤波器的研究已在我们早期的工作中展示 [17, 18]。

此处，我们展示了与近期发展相关的结果，包括在人为构造和实验平衡位形下进行的高能粒子驱动阿尔芬本征模、离子温度梯度（ITG）模以及动力学气球模（KBM）的模拟。具体而言，第4.1节展示了在欧洲联合环（JET）等离子体模拟中多粒子种类处理所表现出的优异计算可扩展性。第4.2节突出了该代码在人为平衡位形下小电子趋肤深度极限内进行电磁模拟的能力。第4.3节展示了在ASDEX-Upgrade等离子体中高能粒子驱动的反剪切诱导阿尔芬本征模的模拟。第4.4节展示了Cyclone基准案例中的ITG和KBM模拟，其结果与GENE代码高度一致。第4.5节展示了在可变位形托卡马克（TCV）中进行的ITG模模拟。第4.6节展示了ITG模和KBM的单谐波及多谐波模拟，验证了该代码在高$\beta$等离子体中的性能。除大量线性基准测试外，第4.5和4.6节还展示了若干非线性模拟结果。

4.1. 多粒子种类模拟的计算性能（JET等离子体）

如图1所示，由于面向对象编程已集成到GKX代码中，只需为所有粒子种类初始化相应实例即可方便地处理多种粒子。关键问题在于随着粒子种类数量增加所带来的计算开销。本研究采用JET（Joint European Torus）案例，因为多种粒子种类对于物理机制的识别至关重要。具体而言，在存在高能离子不稳定性的情况下，已报道放电#99896中具有改善约束性能的稳定氘-氚等离子体 [30]。考虑了九种粒子种类，以评估它们对湍流演化及与阿尔芬模相互作用的潜在影响。

这些粒子种类包括电子、三种热离子（氢、氘、氚）、三种快离子（氢、氘、氦）以及两种杂质粒子（铍和镍）。

回旋动理学模拟在GKK代码中进行，针对$n=5$的环向度诱导阿尔芬本征模（TAE），分别采用3、4、5、6、7和9种粒子组分。所有组分均假设为麦克斯韦分布。我们使用了$16\times 10^6$个电子标记粒子和每种离子组分$10^6$个离子标记粒子，且未进行回旋平均。图3左图展示了典型的二维模结构。为了研究特定粒子组分数下的可扩展性，我们在MPCDF Viper超级计算机上进行了约10小时的模拟，使用2个节点（AMD EPYC Genoa 9554），每个节点配备128个CPU核心，处理器基础频率为3.1 GHz，最大加速频率为3.75 GHz。计算效率以每步所需秒数表示，如图3右图所示。对于3、4、5、6、7和9种组分，总粒子数分别为$N_p=(18,19,20,21,22,24)\times 10^6$，因此归一化效率通过乘以因子$N_p/(18\times 10^6)$计算得出。结果表明，随着组分数目的增加，归一化效率几乎保持不变，显示出良好的组分可扩展性。相关的物理研究将在未来另行发表。

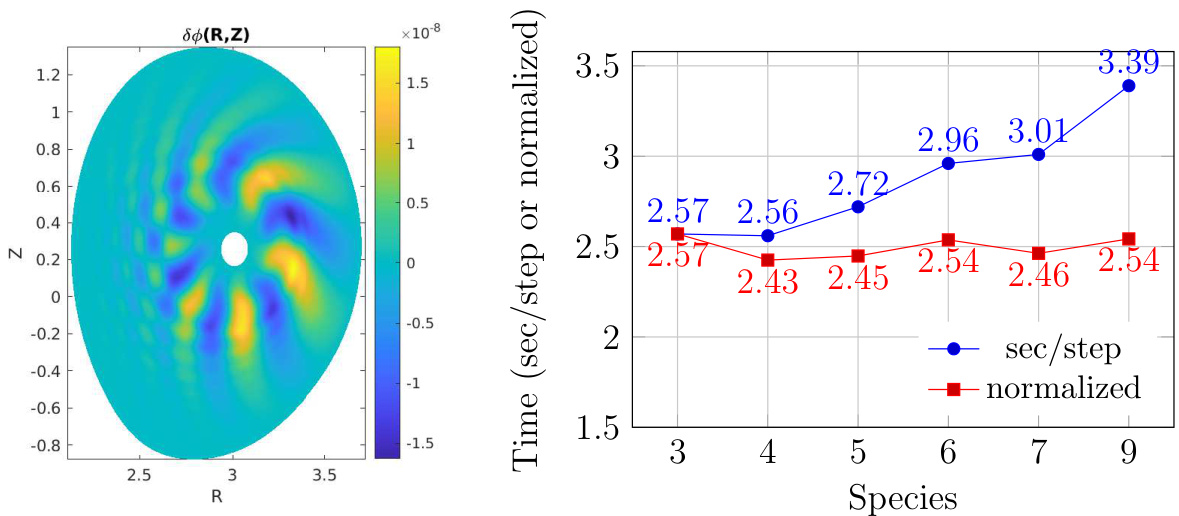
图3：第4.1节JET模拟等离子体中$\delta \Phi$的二维模结构（左）。不同组分数下的每步计算时间和归一化值（右）。

4.2. 高能粒子驱动的环向度诱导阿尔芬本征模（ITPA-TAE）

高能粒子驱动的环向度诱导阿尔芬本征模（TAE）模拟采用由ITPA-EP（国际托卡马克物理活动—高能粒子）小组定义的参数[31]。在此情况下，大半径$R_0=10$ m，小半径$a=1$ m，轴上磁场$B_{\text{axis}}=3$ T，安全因子剖面为$q(r)=1.71+0.16r^2$。电子密度和温度为常数，分别为$n_{\text{e}0}=2.0\times 10^{19}$ m${}^{-3}$和$T_{\text{e}}=1$ keV。电子压强与磁压强之比为${\beta }_{\text{e}}\approx 9\times 10^{-4}$。热离子的拉莫半径为${\rho }_{\text{ti}}=m_{\text{i}}{v}_{\text{ti}}/(e{B}_{\text{axis}})=1.52\times 10^{-3}$ m。采用标称质量比$m_{\text{i}}/m_{\text{e}}=1836$，安培方程左侧绝热部分（$\delta A_{\parallel }^{\text{h}}/d_{\text{e}}^2$）与非绝热部分（${\nabla }_{\perp }^2\delta A_{\parallel }^{\text{h}}$）之比为$1/(d_{\text{e}}^2{k}_{\perp }^2)\approx {\beta }_{\text{e}}/(k_{\perp }{\rho }_{\text{ti}}{)}^2(m_{\text{i}}{T}_{\text{i}}/m_{\text{e}}{T}_{\text{e}})\approx 1.622\times 10^3$，其中$k_{\perp }\approx nq/r=6\times 1.75/0.5=21$。该ITPA-TAE案例的特点是电子趋肤深度较小（$d_{\text{e}}\approx 1.182\times 10^{-3}$ m），若不采用拉回（pullback）方案，则会遭遇“抵消问题”。需要注意的是，本文未使用极向傅里叶滤波器。因此，时间步长（$\Delta t$）比采用结构化网格和傅里叶滤波器的情况[17]小约$1/50$倍（最大$\Delta t\propto k_{\parallel }{v}_{\text{A}}$，其中$k_{\parallel }$为系统中的平行波矢，$v_{\text{A}}$为阿尔芬速度）。

高能粒子（EP）密度剖面由下式给出：

$$\begin{array}{rlr}{n}_{\mathrm{EP}}(r)& =& n_{\mathrm{EP},0}{c}_3\exp \left[-\frac{c_2}{c_1}\tanh \left(\frac{r-c_0}{c_2}\right)\right],\end{array}$$

$$\frac{\mathrm{d}\ln n_{\mathrm{EP}}}{\mathrm{d}r}={\cosh }^{-2}\left(\frac{r-c_0}{c_2}\right),$$

其中归一化类径向坐标$r=\sqrt{(\psi -{\psi }_{\mathrm{axis}})/({\psi }_{\mathrm{edge}}-{\psi }_{\mathrm{axis}})}$，$n_{\mathrm{EP},0}=1.44131\times 10^{17}$ m${}^{-3}$，下标“EP”表示高能粒子，$c_0=0.49123$，$c_1=0.298228$，$c_2=0.198739$，$c_3=0.521298$。基准情况下，高能粒子温度为400 keV。通过施加环向傅里叶滤波器模拟$n=6$模。初始扰动施加于标记粒子权重上，包含两个极向谐波$m=10$和11。共模拟了$32\times 10^6$个电子标记粒子、$4\times 10^6$个离子标记粒子和$4\times 10^6$个高能粒子标记粒子。径向网格数为$N_r=64$。

图4左图展示了$T_{\mathrm{EP}}=400$ keV时极向谐波的径向结构。与EUTERPE的结果吻合较好（ORB5、GYGLES及其他代码的结果见[31]）。右图显示了不同$T_{\mathrm{EP}}$值对应的增长率。GKX的结果与ORB5和GYGLES的趋势一致。需要注意的是，不同代码在回旋中心运动方程的高阶项处理、损失粒子以及梯度的回旋平均等方面采用了不同的处理方法或简化，可能导致增长率相差几个百分点。尽管如此，结果表明GKX在高能粒子驱动TAE的模拟中与其他两种代码具有合理的吻合度。

4.3. ASDEX-Upgrade装置中高能粒子驱动的反剪切阿尔芬本征模（RSAE）（NLED-AUG）

在本节中，我们采用 ASDEX Upgrade（AUG）托卡马克装置第 #31213 次放电在 $t=0.84\text{s}$ 时刻的真实几何位形。这是不同代码和模型中研究高能粒子物理的典型放电案例 [32]。该基准测试结果已在近期发表 [33]。电子、热离子和快粒子的密度与温度剖面如图 5 所示。

在描述高能粒子（EPs）时，我们仅考虑有限轨道宽度（FOW）效应，忽略有限拉莫半径（FLR）效应，以便与其他代码的结果进行比较 [33]。电子、热离子和快离子的标记粒子数分别为 $16\times 10^6$、$10^6$ 和 $10^6$。本案例中采用的离子-电子质量比为

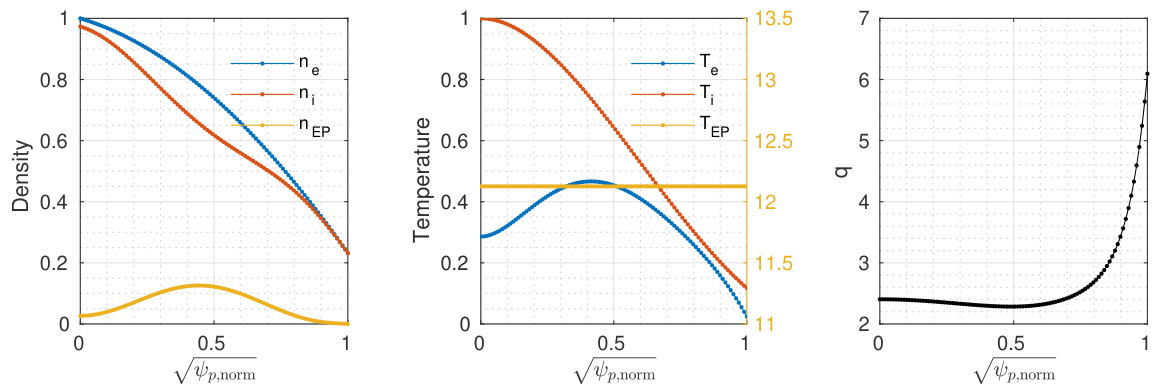
图 5：第 4.3 节 NLED-AUG 案例中电子、热离子和快粒子的密度（左）、温度（中）剖面。密度和温度分别归一化为 $n_{\mathrm{ref}}=1.7159\times 10^{19}/{\mathrm{m}}^3$ 和 $T_{\mathrm{ref}}=2.4741\times 10^3\mathrm{eV}$。安全因子的径向剖面（右）。

$m_{\mathrm{i}}/m_{\mathrm{e}}=500$。时间步长为 $\Delta t/t_N=0.004$，其中 $t_N$ 是第 3.2 节中定义的代码时间单位。二维截面上的模结构以及极向傅里叶谐波的径向结构如图 6 所示。二维模结构与使用 HYMAGYC 代码模拟的结果相似，而极向谐波的径向结构与之前报道的 ORB5 代码结果一致 [33]。图 7 显示了增长率随高能粒子温度的变化。ORB5 和 GKK 的结果彼此更为接近，因为二者均采用回旋动理学等离子体模型，而 MEGA 和 HYMAGYC 则是混合磁流体力学-动理学代码。

4.4. 离子温度梯度模与动力学气球模（Cyclone）

GA-STD 案例（芯部）参数基于 DIII-D 托卡马克等离子体，并已被用于先前的基准研究工作 [34]。采用同心圆形磁通面。平衡密度和温度剖面记为 $H(\tilde{r})$，其归一化对数梯度 $R_0/L_{\mathrm{H}}$ 由下式给出：

$$\frac{H(r)}{H(r_0)}=\exp \left[-{\kappa }_{\mathrm{H}}{w}_{\mathrm{H}}\frac{a}{R_0}\tanh \left(\frac{r-r_0}{w_{\mathrm{H}}a}\right)\right],$$

其中 $r=\sqrt{(R-R_{\mathrm{axis}}{)}^2+(Z-Z_{\mathrm{axis}}{)}^2}$，$L_{\mathrm{H}}=-[\mathrm{d}\ln H(r)/\mathrm{d}r{]}^{-1}$ 是剖面 $H(r)$ 的特征长度，$r_0=a/2$。离子-电子质量比为 $m_{\mathrm{i}}/m_{\mathrm{e}}=1836$，且仅考虑氘离子（$m_{\mathrm{i}}/m_{\mathrm{p}}=2$），其中 $m_{\mathrm{p}}$ 为质子质量。轴上磁场 $B_0=2\mathrm{T}$，${\rho }^{\ast }\equiv {\rho }_{\mathrm{i}}/a=1/180$，${\rho }_{\mathrm{i}}=\sqrt{2T_{\mathrm{i}}{m}_{\mathrm{i}}/(e{B}_0)}$，纵横比 $ϵ=a/R_0=0.36$，$T_{\mathrm{e}}/T_{\mathrm{i}}=1$，温度和密度剖面的特征长度分别为 $R_0/L_{T_{\mathrm{i}}}=-(\mathrm{d}\ln T_{\mathrm{i}}/\mathrm{d}\mathrm{r}{)}^{-1}=6.96$，$R_0/L_{T_{\mathrm{e}}}=-(\mathrm{d}\ln T_{\mathrm{e}}/\mathrm{d}\mathrm{r}{)}^{-1}=6.96$，$R_0/L_n=-(\mathrm{d}\ln n/\mathrm{d}\mathrm{r}{)}^{-1}=2.23$，碰撞频率 ${\nu }_{\mathrm{coll}}=0$。

模拟区域为 $r/a\in [0.1,0.9]$。对于低 $\beta$ 情况，模拟了 $256\times 10^6$ 个电子和 $4\times 10^6$ 个离子。由于 pullback-mixed 变量方案在磁流体力学（MHD）极限下表现更优，因此在高 $\beta$ 情况下所需的电子数量较少。对于高 $\beta$ 情况，使用了 $128\times 10^6$ 个电子和 $10^6$ 个离子。时间步长为 $0.0005t_N$。模拟在 Viper 超级计算机的两个节点（对应 $128\times 10^6$ 个电子）或四个节点（对应 $256\times 10^6$ 个电子）上运行。典型的模拟需运行 $24\sim 48$ 小时，以覆盖至少 $10R_N/v_N$ 的时间，直至观察到指数增长，从而计算增长率。

不同 $\beta$ 值下的增长率列于表 1。GKX 结果与 GENE 结果之间取得了良好的一致性 [34]。图 8 显示了单个环向谐波 $n=19$ 模拟中标量势 $\delta \Phi$ 和平行矢势 $\delta A_{\parallel }$ 的二维模结构。在 $\delta \Phi$ 的气球结构方面，$\beta =0.001$ 时的 ITG 模结构与 $\beta =0.025$ 时相似。然而，$\delta \Phi$ 与 $\delta A_{\parallel }$ 最大幅值之比有所不同。对于 $\beta =0.001$ 的 ITG 模，$|\delta \Phi /\delta A_{\parallel }|\gtrsim 50$；而对于 $\beta =0.025$ 的 KBM 模，$|\delta \Phi /\delta A_{\parallel }|\approx 4$。

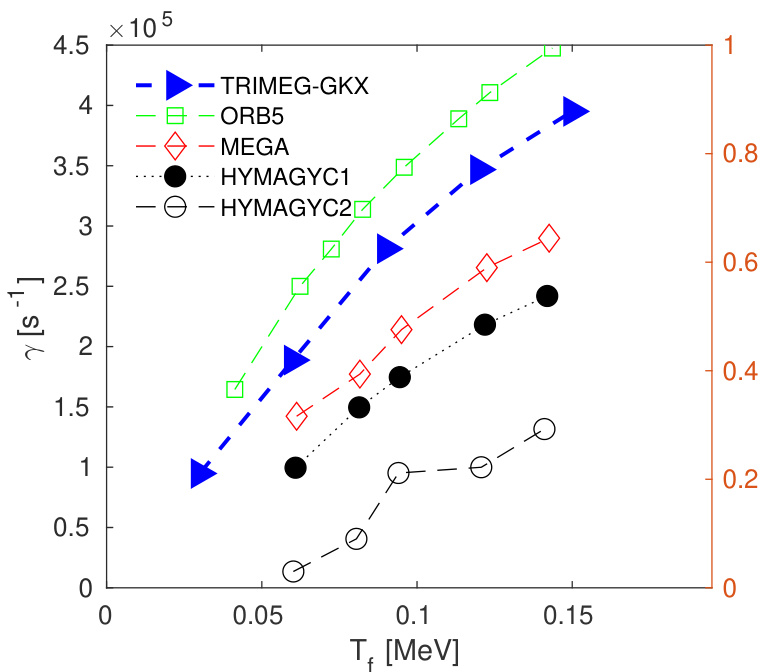
图7：第4.3节中研究的GKK及其他代码[33]得到的增长率与高能粒子温度的关系。

该趋势与之前GKNET中进行的ITG-KBM模拟结果一致[35]。

$\beta$	$\gamma [c_s/R_0](\text{GKK})$	$\gamma [c_s/R_0](\text{GENE})$
$0.001$	$0.533$	$0.528$
$0.020$	$1.012$	$0.989$
$0.025$	$1.442$	$1.467$

表1：不同$\beta$值下GKX与GENE[34]的增长率对比。

4.5. TCV装置中的静电离子温度梯度模

TCV-X21案例已在可变位形托卡马克（Tokamak à configuration variable, TCV）上进行了实验和数值研究[36, 37, 38]。该案例被GRILLIX和GENE-X等多种代码用于考虑分离面（separatrix）条件下的输运及剖面生成研究。本节进行芯部等离子体模拟，以展示线性ITG不稳定性基本特征。单-$n$模拟采用静电模型。参考拉莫尔半径为${\rho }_N=0.39012$ cm，参考磁场为$B_{\mathrm{ref}}=0.90727$ T，所用离子-电子质量比为100。

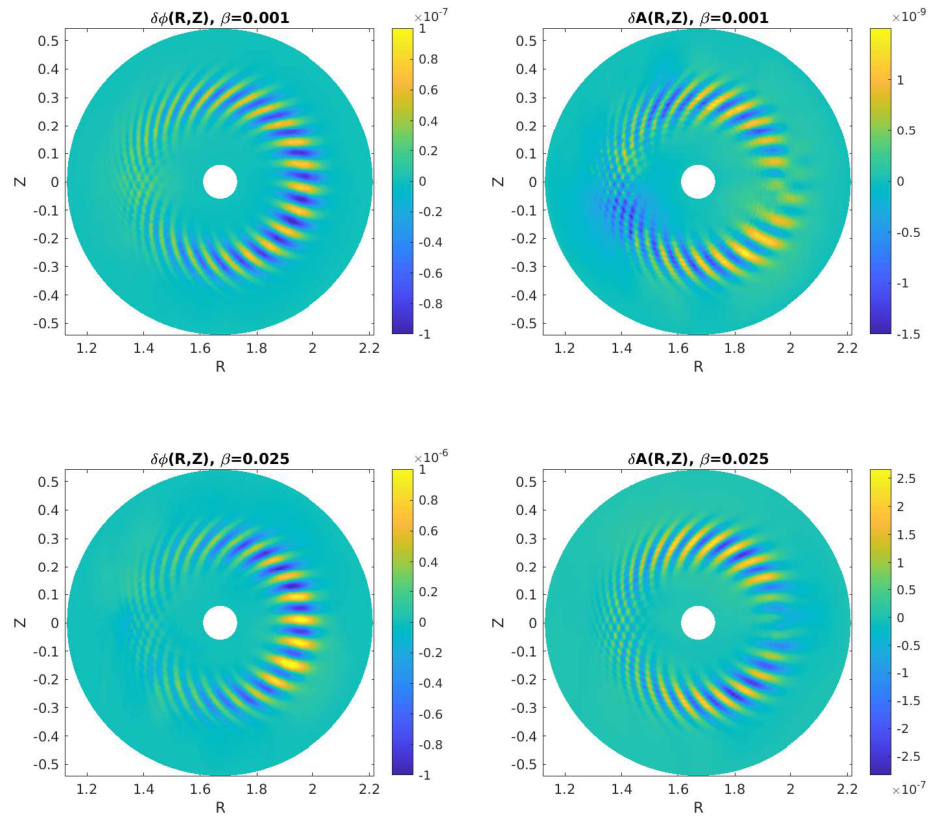
图8：第4.4节Cyclone案例在不同$\beta$值下的$\delta \varphi$和$\delta A_{\parallel }$二维模结构。上图：$\beta =0.001$时的ITG模，$|\delta \Phi /\delta A_{\parallel }|\gtrsim 50$；下图：$\beta =0.025$时的KBM模，$|\delta \Phi /\delta A_{\parallel }|\approx 4$。

图9展示了$n=10$谐波在线性和非线性初期阶段的模结构。非线性模结构在径向方向展宽，这与我们之前的观测结果一致[20, 18]。图10展示了$n=10$谐波的时间演化过程。该模通过波-粒子非线性相互作用达到饱和。我们选取指数增长阶段的数据计算增长率。图10右图展示了不同$n$谐波的增长率。在未考虑有限拉莫尔半径效应的模拟中，增长率随环向模数$n$增大而增加，直至$n\le 20$，此时有限轨道效应变得显著。考虑有限拉莫尔半径效应后，ITG增长率在$n\in [10,15]$范围内最大。

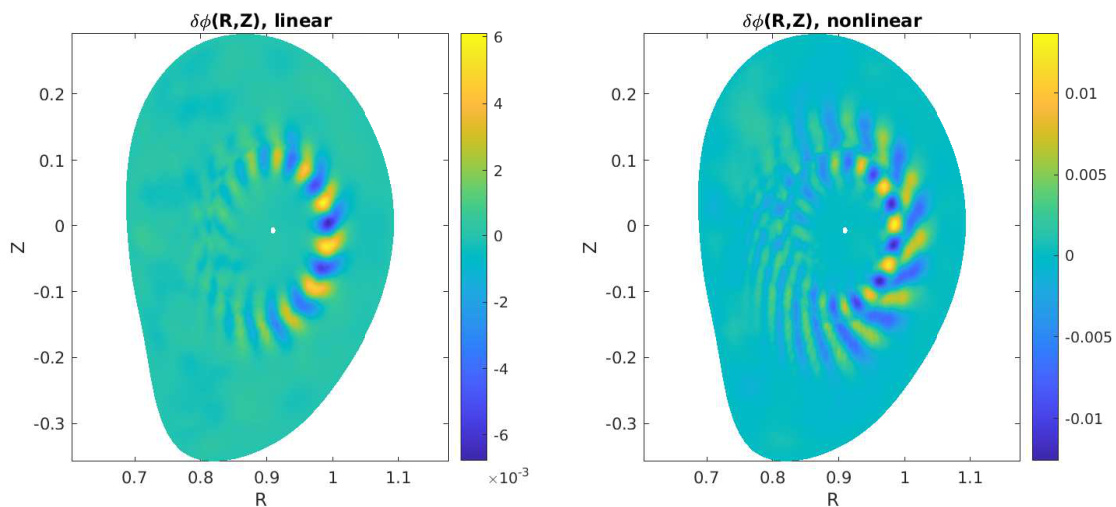
图9：TCV托卡马克等离子体中$n=10$ ITG模的线性及非线性初期阶段模结构（第4.5节）。

4.6. 具有$(n,\beta )$依赖性的ITG模/KBM电磁模拟

采用经济型Cyclone案例，利用2D1F求解器和三维分段场对齐有限元方法，对ITG模和KBM进行多-$n$模拟。通过将离子-电子质量比$m_{\mathrm{i}}/m_{\mathrm{e}}$设为100（而非1836），时间步长$\Delta t$可增大$\sim \sqrt{18.36}\approx 4.285$倍。此外，通过将${\rho }^{\ast }\equiv {\rho }_{\mathrm{i}}/a$设为100（而非180），计算成本降低约$1/1.8^3\approx 1/5.832$倍。总体计算成本因此降低约25倍。

对不同$\beta$值下的$n=10$环向谐波进行了模拟。该经济型Cyclone案例也曾由GKNET代码研究过[35]。如图11左图所示，除ITG-KBM过渡区域（$1.2\%<\beta <1.5\%$）存在微小差异外，GKX结果与GKNET结果基本一致。该差异可能源于平衡态处理及回旋平均中高阶项的不同。然而，对于大多数$\beta$值，两者吻合良好。

进行了两组模拟，分别对应 $\beta =0.5\%$ 和 $2\%$。单-$n$ 模拟使用 2D1F 求解器，以确定不同 $n$ 值下的线性增长率。每个单-$n$ 模拟使用 $1\times 10^6$ 个离子，并采用 4 点回旋平均。大多数情况使用 $16\times 10^6$ 个电子，但对于 $n\ge 18$ 的情况，则需要 $32\times 10^6$ 个电子。对于 $\beta =0.5\%$，最大

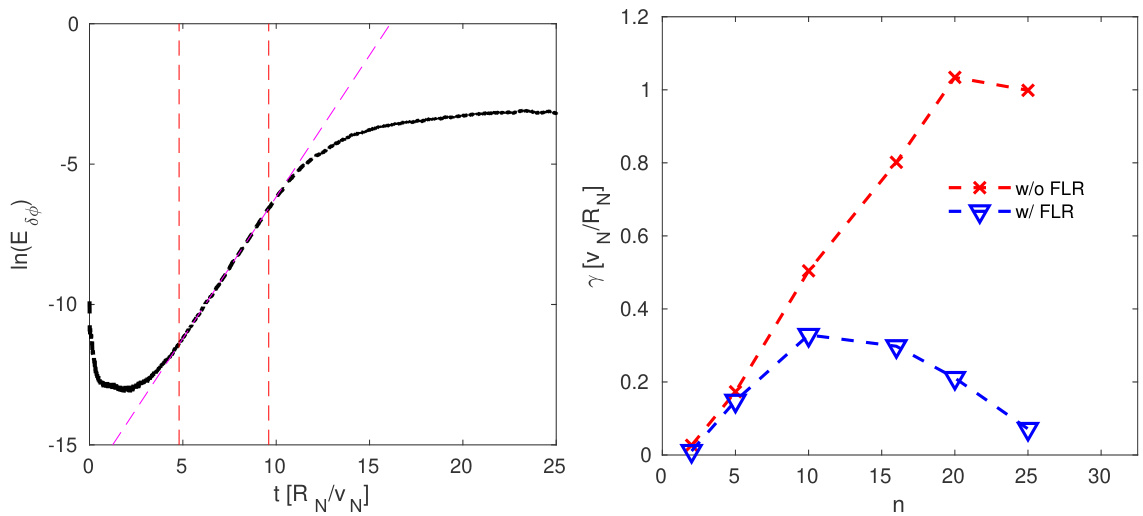
图 10：左图：$n=10$ 模拟的时间演化，其中垂直虚线表示用于计算增长率的数据区间，品红色虚线表示根据拟合增长率构建的拟合时间演化曲线。右图：ITG 模式的增长率随环向模数 $n$ 的变化关系，分别考虑和不考虑热离子有限拉莫尔半径效应（见第 4.5 节）。

增长率出现在 $n\approx 12$ 处；而对于 $\beta =2\%$，最大增长率出现在 $n\approx 7$ 处，如图 11 右图所示。随着 $\beta$ 增大，最不稳定环向谐波的环向模数 $n$ 向低值移动，且最大增长率增大，如图所示，这与先前的理论分析一致 [39]。三维模拟在马克斯·普朗克等离子体物理研究所的 TOK 集群上运行，使用了 32 个节点（AMD Genoa EPYC 9354），每个节点配备 32 个 CPU 核心，处理器基础频率为 3.25 GHz，最大加速频率为 3.8 GHz。关于静电 ITG 模式的多-$n$ 模拟可参见我们之前的工作 [18]。本文仅展示了 $\beta =2\%$ 下 KBM 的多-$n$ 模拟。非线性模拟从纯噪声初始条件开始，总共模拟了 $64\times 10^6$ 个电子标记粒子和 $10^6$ 个离子标记粒子。时间步长为 $\Delta t=0.005t_N$。每个 $R_N/v_N$ 的计算耗时约 1.5 小时。$n$ 谱在指数增长阶段结束时测量，如图 12 所示。$n$ 谱在 $n=7$ 处的峰值与线性增长率的结果一致。最不稳定的 $n$ 分量增长最快，因此利用总场能量计算出的增长率接近最不稳定模的增长率。图 13 给出了 $r/a=0.5$ 通量面内模结构随极向和环向坐标的分布。

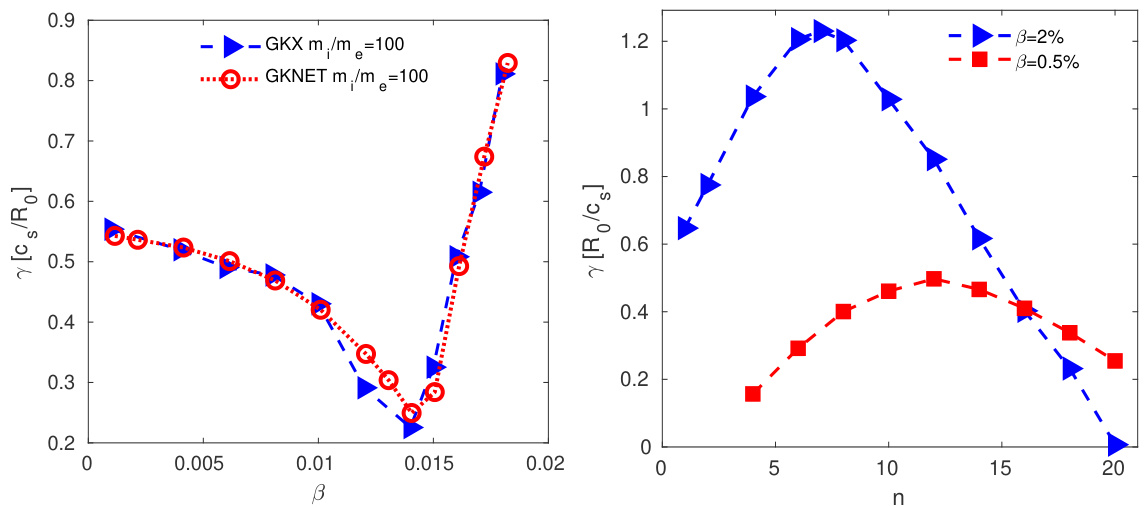
图 11：左图：ITG 模式/KBM 的增长率随 $\beta$ 的变化，并与 GKNET 使用经济型 Cyclone 参数（见第 4.6 节）的结果进行比较。右图：$\beta =0.5\%$ 和 $2\%$ 下增长率随环向模数 $n$ 的变化。

场对齐结构由分段场对齐有限元求解器捕捉，如左图所示。在更密的 $(\theta ,\varphi )$ 网格上对场值进行插值，右图展示了傅里叶分量 $\delta {\varphi }_{m,n}(r)$。其幅值峰值出现在 $nq=m$ 附近，主导谐波集中在 $n=7$ 附近，这与图 12 所示的 $n$ 谱一致。尽管本文聚焦于 GKK 代码在多-$n$ 模拟中的数值研究，更多物理方面的研究成果将在另一篇工作中报道。

5. 结论

TRIMEG-GKK 代码集成了电磁特性、场对齐有限元方法、多粒子种类处理能力、回旋中心运动方程中强形式的严格处理、单谐波或多谐波模拟的高度灵活性以及缓存优化技术，这些特性在其他回旋动理学代码中构成了独特的组合。这些功能使其成为研究芯部等离子体中湍流和高能粒子（EP）动力学的强大工具。本文总结了 TRIMEG-GKK 代码的最新进展，重点介绍了其底层物理模型、数值方法和代表性模拟结果。代码的关键特性和进展包括：

1. 采用面向对象编程，便于灵活高效地实现多粒子种类模拟。

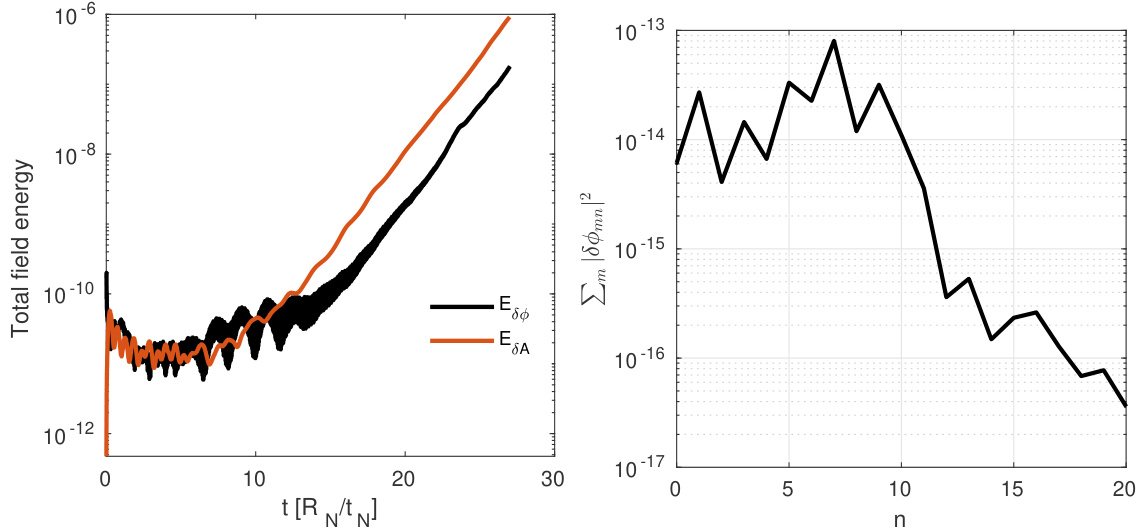
图 12：$\beta =2\%$ 下 KBM 多谐波模拟（见第 4.6 节）中总场能量的时间演化（左图）及线性阶段的 $n$ 谱（右图）。

2. 开发了分段场对齐有限元方法，提高了沿磁场方向的网格效率，显著提升了多-$n$ 模拟的性能。

3. 实现了缓存优化技术，提高了在粒子位置插值扰动场数据时的内存访问效率，在无需粒子排序的情况下，典型单谐波模拟速度提升达十倍。

4. 在电磁回旋中心运动方程中对强形式进行了严格处理，提高了 pullback-混合变量格式的精度和稳定性，从而使得模拟无需依赖傅里叶滤波器和数值缓冲区。

数值基准测试证实了 TRIMEG-GKK 代码能够模拟多种微观和宏观不稳定性，包括由高能粒子驱动的阿尔芬本征模、离子温度梯度（ITG）模以及动力学气球模。这些能力已在特设平衡位形和实验重构的平衡位形（例如来自 ASDEX Upgrade（AUG）、可变位形托卡马克（TCV）以及欧洲联合环（JET））中得到验证。未来的工作将聚焦于非线性物理的研究，并系统性地开展验证与确认工作。计划中的开发内容包括处理开放磁力线位形和碰撞效应，这将基于我们之前的工作 [40]，并与 TRIMEG-C1 代码 [22] 的开发相结合。

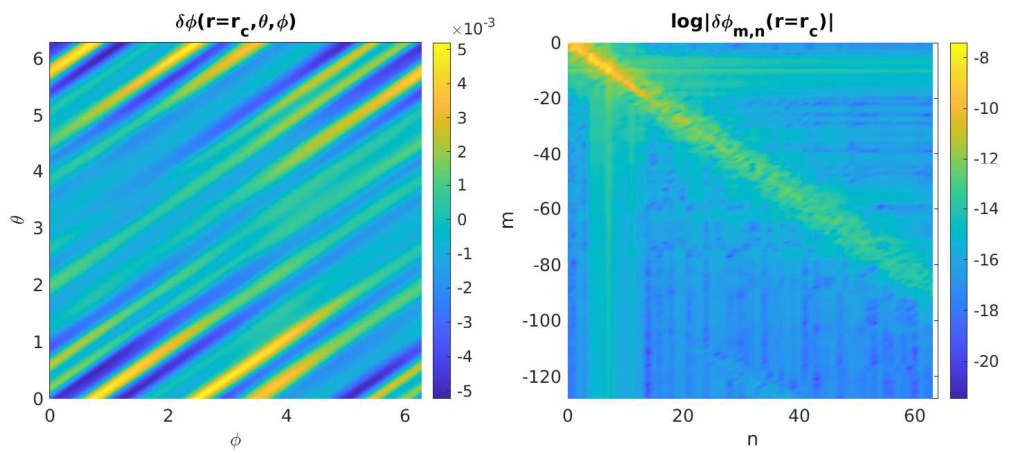
图 13：在 $r/a=0.5$ 的磁通面上，线性模结构随极向和环向坐标的分布（左），及其傅里叶分量（右）。

致谢

Z.X. Lu 感谢 Alexey Mishchenko、Peiyou Jiang、Ralf Kleiber、Matthias Borchardt、Eric Sonnendrücker 和 Fulvio Zonca 富有成效的讨论。本文中的模拟计算在 TOK 集群以及 MPCDF Viper/Raven 超级计算机上完成。感谢 Eurofusion 项目 TSVV-8、ACH/MPG 和 ATEP 的支持。本工作是在 EUROfusion 联盟框架下开展的，该联盟由欧洲联盟通过 Euratom 研究与培训计划资助（资助协议编号 101052200—EUROfusion）。然而，文中表达的观点和意见仅代表作者，并不一定反映欧洲联盟或欧洲委员会的观点。欧洲联盟及欧洲委员会对此不承担任何责任。

附录 A. $(r,\varphi ,\theta )$ 坐标系下的回旋中心运动方程

平衡态下的平行速度和磁漂移速度由下式给出：

$${\dot{r}}_0=b_0^{\ast r}{v}_{||}+C_d\frac{F}{J}{\partial }_{\theta }B,$$

$$\begin{array}{rlr}{\dot{\theta }}_0& =& b_0^{\ast \theta }{v}_{\parallel }-C_d\frac{F}{J}{\partial }_{r}B,\end{array}$$

$$\begin{array}{rlr}\dot{{\varphi }_0}& =& b_0^{\ast \varphi }{v}_{\parallel }+C_d\frac{{\partial }_r\psi }{R^2}(g^{rr}{\partial }_{r}B+g^{r\theta }{\partial }_{\theta }B)\end{array}$$

$$C_d=\frac{{\bar{m}}_s}{{\bar{e}}_s}{\rho }_N\frac{B_{\mathrm{ref}}}{B{B}_{||}^{\ast }}\mu ,$$

其中 $b_0^{\alpha }\equiv {\mathbf{b}}_0\cdot \nabla \alpha$ 是 ${\mathbf{b}}_0$ 的逆变分量，$g^{\alpha \beta }\equiv \nabla \alpha \cdot \nabla \beta$ 是度规张量。主导阶项如下所示

$$\begin{array}{rlr}{\dot{r}}_0& =& C_d\frac{F}{J}{\partial }_{\theta }B,\end{array}$$

$$\begin{array}{rlr}{\dot{\theta }}_0& =& \frac{B^{\theta }}{B}{v}_{\parallel }-C_d\frac{F}{J}{\partial }_{r}B,\end{array}$$

$$\begin{array}{rlr}{\dot{\varphi }}_0& =& \frac{B^{\varphi }}{B}{v}_{\parallel }+C_d\frac{{\partial }_r\psi }{R^2}(g^{rr}{\partial }_{r}B+g^{r\theta }{\partial }_{\theta }B),\end{array}$$

$$C_d=\frac{{\bar{m}}_s}{{\bar{e}}_s}{\rho }_N\frac{B_{\mathrm{ref}}}{B^3}(v_{\parallel }^2+\mu B),$$

其中 $B^{\alpha }\equiv \mathbf{B}\cdot \nabla \alpha$ 是平衡磁场的逆变分量，且在磁漂移项中，磁曲率被近似地替换为磁场梯度。

由镜像力引起的方程为

$${\dot{v}}_{\parallel ,0}=-\frac{\mu }{JB}{\partial }_r\psi {\partial }_{\theta }B.$$

关于扰动运动方程，平衡变量在 $(r,\varphi ,\theta )$ 坐标系中计算，但 ${\partial }_r⟨\delta \Phi ⟩$、${\partial }_{\theta }⟨\delta \Phi ⟩$ 和 ${\partial }_{\varphi }⟨\delta \Phi ⟩$ 则在 $r,\varphi ,\eta$ 坐标系中计算。特别地，$\mathbf{b}\cdot \nabla ⟨\delta \Phi ⟩$ 直接在 $(r,\varphi ,\eta )$ 坐标系中利用 $\mathbf{b}\cdot \nabla =\mathbf{b}\cdot \nabla \varphi \partial /\partial \varphi {|}_{r,\eta }$ 进行计算。

$E\times B$ 速度由下式给出：

$$\begin{array}{rlr}{\dot{r}}_1& =& -C_{E,\theta }{g}^{rr}{\partial }_{\varphi }⟨\delta G⟩+C_{E,\varphi }{\partial }_{\theta }⟨\delta G⟩-\frac{{\bar{e}}_s}{{\bar{m}}_s}⟨\delta A_{\parallel }^h⟩b^{\ast ,r}\\ & & \end{array}.$$

$$\begin{array}{rlr}{\dot{\theta }}_1& =& -C_{E,\theta }{g}^{r\theta }{\partial }_{\varphi }⟨\delta G⟩-C_{E,\varphi }{\partial }_r⟨\delta G⟩-\frac{{\bar{e}}_s}{{\bar{m}}_s}⟨\delta A_{\parallel }^h⟩b^{\ast ,\theta }\end{array}$$

$${\dot{\varphi }}_1=C_{E,\theta }\left(g^{rr}{\partial }_r⟨\delta G⟩+g^{r\theta }{\partial }_{\theta }⟨\delta G⟩\right)-\frac{{\bar{e}}_s}{{\bar{m}}_s}⟨\delta A_{\parallel }^h⟩b^{\ast ,\varphi }$$

$$C_{E,\theta }={\rho }_{\mathrm{ref}}{B}_{\mathrm{ref}}\frac{{\partial }_r\psi }{B^2{R}^2},C_{E,\varphi }={\rho }_{\mathrm{ref}}{B}_{\mathrm{ref}}\frac{F}{J{B}^2},$$

其中 $\delta G=\delta \Phi -v_{\parallel }\delta A_{\parallel }$，${\partial }_r⟨\delta G⟩$、${\partial }_{\theta }⟨\delta G⟩$ 和 ${\partial }_{\varphi }⟨\delta G⟩$ 均在 $(r,\varphi ,\theta )$ 坐标系中表示。若采用三维场对齐的有限元法（FEM）求解器，则需从 Clebsch 坐标 $(r,\varphi ,\eta )$ 出发计算 ${\partial }_r\delta G$、${\partial }_{\theta }\delta G$ 和 ${\partial }_{\varphi }\delta G$。利用链式法则，可得

$${\partial }_r{|}_{\varphi ,\theta }={\partial }_r{|}_{\varphi ,\eta }+({\partial }_r\eta ){\partial }_{\eta },$$

$$\begin{array}{rlr}{\partial }_{\theta }{|}_{r,\varphi }& =& ({\partial }_{\theta }\eta ){\partial }_{\eta },\end{array}$$

$$\begin{array}{rlr}{\partial }_{\varphi }{|}_{r,\theta }& =& {\partial }_{\varphi }{|}_{r,\eta }+({\partial }_{\varphi }\eta ){\partial }_{\eta }\end{array}$$

回旋平均量 $⟨\delta \Phi ⟩$ 在 $(r,\theta ,\varphi )$ 坐标系中计算。平行扰动场的贡献为

$$-\frac{e_s}{m_s}\mathbf{b}\cdot \nabla ⟨\delta \Phi ⟩=-\frac{e_s}{m_s}\frac{B^{\varphi }}{B}{\partial }_{\varphi }{|}_{r,\eta }⟨\delta \Phi ⟩.$$

References

[1] W. W. Lee, Gyrokinetic approach in particle simulation, Phys. Fluids 26 (1983) 556.

[2] Z. Lin, T. S. Hahm, W. W. Lee, W. M. Tang, R. B. White, Turbulent transport reduction by zonal flows: Massively parallel simulations, Science 281 (1998) 1835–1837.

[3] C. Chang, S. Ku, G. Tynan, R. Hager, R. Churchill, I. Cziegler, M. Greenwald, A. Hubbard, J. Hughes, Fast low-to-high confinement mode bifurcation dynamics in a tokamak edge plasma gyrokinetic simulation, Phys. Rev. Lett. 118 (2017) 175001.

[4] R. Hatzky, R. Kleiber, A. Königies, A. Mishchenko, M. Borchardt, A. Bottino, E. Sonnendrücker, Reduction of the statistical error in electromagnetic gyrokinetic particle-in-cell simulations, Journal of Plasma Physics 85 (2019).

[5] Y. Chen, S. E. Parker，基于真实平衡剖面与几何结构的电磁回旋动理学δf粒子模拟湍流研究，《计算物理杂志》220 (2007) 839–855。

[6] A. Mishchenko, A. Bottino, A. Biancalani, R. Hatzky, T. Hayward-Schneider, N. Ohana, E. Lanti, S. Brunner, L. Villard, M. Borchardt 等，ORB5 中拉回（Pullback）格式的实现，《计算机物理通信》238 (2019) 194–202。

[7] Z. X. Lu, G. Meng, M. Hoelzl, P. Lauber，用于阿尔芬波及高能粒子物理电磁粒子模拟的隐式全f方法的发展，《计算物理杂志》440 (2021) 110384。

[8] B. J. Sturdevant, S. Ku, L. Chacón, Y. Chen, D. Hatch, M. Cole, A. Sharma, M. Adams, C. Chang, S. Parker 等，xgc 代码中电磁回旋动理学 ${\nu }_{\parallel }$ 形式下全隐式粒子模拟方法的验证，《等离子体物理》28 (2021) 072505。

[9] L. Chen, H. Chen, F. Zonca, Y. Lin，磁化等离子体中低频电磁涨落的回旋动理学模拟模型，《中国科学：物理学 力学 天文学》64 (2021) 245211。

[10] M. Rosen, Z. Lu, M. Hoelzl，托卡马克等离子体中动力学阿尔芬波的 e 和 b 回旋动理学模拟模型，《等离子体物理》29 (2022)。

[11] J. Bao, Z. Lin, Z. Lu，一种用于含动力学电子磁化等离子体电磁模拟的守恒格式，《等离子体物理》25 (2018)。

[12] E. Lanti, N. Ohana, N. Tronko, T. Hayward-Schneider, A. Bottino, B. F. McMillan, A. Mishchenko, A. Scheinberg, A. Biancalani, P. Angelino 等，ORB5：采用粒子模拟方法在环形几何中的全局电磁回旋动理学代码，《计算机物理通信》251 (2020)。

[13] R. Kleiber, M. Borchardt, R. Hatzky, A. Königies, H. Leyh, A. Mishchenko, J. Riemann, C. Slaby, J. García-Régañña, E. Sanchez 等，EUTERPE：适用于仿星器几何的全局回旋动理学代码，《计算机物理通信》295 (2024) 109013。

[14] S. Taimourzadeh, E. Bass, Y. Chen, C. Collins, N. Gorelenkov, A. Königies, Z. Lu, D. A. Spong, Y. Todo, M. Austin 等，聚变等离子体中高能粒子集成模拟的验证与确认，《核聚变》59 (2019) 066006。

[15] M. Kraus, K. Kormann, P. J. Morrison, E. Sonnendrücker，GEMPIC：几何电磁粒子模拟方法，《等离子体物理杂志》83 (2017) 905830401。

[16] G. Meng, K. Kormann, E. Poulsen, E. Sonnendruecker，漂移动理学与全动理学Vlasov-Maxwell方程的几何粒子模拟离散化方法，《等离子体物理与受控核聚变》(2025)。

[17] Z. X. Lu, G. Meng, R. Hatzky, M. Hoelzl, P. Lauber, 全f和δf回旋动理学粒子模拟阿尔芬波与高能粒子物理, 《Plasma Physics and Controlled Fusion》(2023).

[18] Z. X. Lu, G. Meng, E. Sonnendrücker, R. Hatzky, A. Mishchenko, F. Zonca, P. Lauber, M. Hoelzl, 用于托卡马克等离子体中多模非线性粒子模拟的分段场对齐有限元方法, 《Journal of Plasma Physics》91 (2025) E48.

[19] G. Meng, P. Lauber, Z. X. Lu, X. Wang, 非微扰模结构对高能粒子输运的影响, 《Nuclear Fusion》60 (2020) 056017.

[20] Z. X. Lu, P. Lauber, T. Hayward-Schneider, A. Bottino, M. Hoelzl, 面向真实托卡马克几何下全等离子体回旋动理学模拟的非结构网格方法的开发与测试, 《Phys. Plasmas》26 (2019) 122503.

[21] L. Rekhviashvili, Z. Lu, M. Hoelzl, A. Bergmann, P. Lauber, trimeg代码中托卡马克等离子体新经典电子输运与自举电流产生的回旋动理学模拟, 《Physics of Plasmas》30 (2023).

[22] Z. X. Lu, G. Meng, R. Hatzky, E. Sonnendrücker, A. Mishchenko, P. Lauber, F. Zonca, M. Hoelzl, 基于三角网格与C¹有限元的回旋动理学电磁粒子模拟, 《Plasma Physics and Controlled Fusion》67 (2024) 015015.

[23] A. Mishchenko, A. Königies, R. Kleiber, M. Cole, 回旋动理学电磁模拟中的拉回变换, 《Physics of Plasmas》21 (2014).

[24] A. Mishchenko, M. Borchardt, R. Hatzky, R. Kleiber, A. Königies, C. Nührenberg, P. Xanthopoulos, G. Rober-Clark, G. G. Plunk, 仿星器等离子体中电磁湍流的全局回旋动理学模拟, 《Journal of Plasma Physics》89 (2023) 955890304.

[25] J. Williams, Bspline-Fortran, 2008. https://github.com/jacobwilliams/bspfortran.

[26] Z. X. Lu, F. Zonca, A. Cardinali, 托卡马克等离子体中波包传播的理论与数值研究, 《Physics of Plasmas》19 (2012).

[27] O. Sauter, S. Y. Medvedev, 托卡马克坐标约定：COCOS, 《Computer Physics Communications》184 (2013) 293–302.

[28] H. Lütjens, A. Bondeson, O. Sauter, 用于环形磁流体平衡计算的chease代码, 《Computer Physics Communications》97 (1996) 219–260.

[29] G. Meng, P. Lauber, X. Wang, Z. Lu, 反剪切阿尔芬本征模的模结构对称性破缺及其对高能粒子分布中平行速度不对称性生成的影响, Plasma Science and Technology 24 (2022) 025101.

[30] J. Garcia, Y. Kazakov, R. Coelho, M. Dreval, E. de la Luna, E. R. Solano, Ž. Šancar, J. Varela, M. Baruzzo, E. Belli 等, 在高能离子不稳定性存在下实现具有改善约束性能的稳定氘氚等离子体, Nature Communications 15 (2024) 7846.

[31] A. Königies, S. Briguglio, N. Gorelenkov, T. Fehér, M. Isaev, P. Lauber, A. Mishchenko, D. A. Spong, Y. Todo, W. A. Cooper 等, 快粒子驱动TAE动力学线性计算的回旋动理学、动理学MHD与回旋流体代码基准测试, Nucl. Fusion 58 (2018) 126027.

[32] P. Lauber, B. Geiger, G. Papp, L. Guimarais, P. Z. Poloskei, V. Igochine, M. Maraschek, G. Pokol, T. Hayward-Schneider, Z. Lu 等, ASDEX Upgrade中芯部杂质累积情形下强非线性高能粒子动力学, 第27届IAEA聚变能大会论文集 (2018).

[33] G. Vlad, X. Wang, F. Vannini, S. Briguglio, N. Carlevaro, M. Falessi, G. Fogaccia, V. Fusco, F. Zonca, A. Biancalani 等, 利用NLED-AUG测试案例对HYMAGYC、MEGA和ORB5代码进行阿尔芬模（由高能粒子驱动）的线性基准比较, Nuclear Fusion 61 (2021) 116026.

[34] T. Görler, N. Tronko, W. A. Hornsby, A. Bottino, R. Kleiber, C. Norscini, V. Grandgirard, F. Jenko, E. Sonnendrücker, 回旋动理学全局电磁模的代码间比较, Phys. Plasmas 23 (2016).

[35] A. Ishizawa, K. Imadera, Y. Nakamura, Y. Kishimoto, 动理学气球模驱动湍流的全局回旋动理学模拟, Physics of Plasmas 26 (2019).

[36] D. Oliveira, T. Body, D. Galassi, C. Theiler, E. Laribi, P. Tamain, A. Stegmeir, M. Giacomin, W. Zholobenko, P. Ricci 等, 针对TCV-X21偏滤器L模参考案例的边界湍流代码验证, Nuclear Fusion 62 (2022) 096001.

[37] T. A. J. Body, 面向边界与偏滤器的湍流模拟开发及实验验证, 博士学位论文, 慕尼黑工业大学, 2022.

[38] P. Ulbl, T. Body, W. Zholobenko, A. Stegmeir, J. Pfennig, F. Jenko, 碰撞效应对TCV边界及刮削层中全局回旋动理学模拟验证的影响, Physics of Plasmas 30 (2023).

[39] K. Aleynikova, A. Zocco, 简单几何位形下动理学气球模理论的定量研究, Physics of Plasmas 24 (2017).

[40] Z. X. Lu, G. Meng, T. Tyranowski, A. Chankin, 粒子模拟中Rosenbluth-Trubnikov碰撞算子的高阶随机积分格式, Journal of Computational Physics (2025) 113811.