全 $f$ 与 $\delta f$ 回旋动理学粒子模拟阿尔芬波与高能粒子物理

卢志新、孟果、Roman Hatzky、Matthias Hoelzl、Philipp Lauber

本文聚焦于粒子-网格（particle-in-cell, PIC）方法的发展及其在托卡马克等离子体中阿尔芬波和高能粒子物理研究中的应用。$\delta f$ 与全 $f$ 方案在统一框架下构建，采用混合变量及针对电磁问题的拉回（pullback）方案。TRIMEG-GKX 程序 [Lu et al., J. Comput. Phys. 440 (2021) 110384] 已通过三次样条有限元方法以及全 $f$ 和 $\delta f$ 方案进行了升级。我们对 ITPA-TAE 案例中的高能粒子（EP）驱动的环向阿尔芬本征模（TAE）进行了模拟，该案例以极小的电子趋肤深度（约 $1.18\times 10^{-3}$ 米）为特征，这对电磁模拟而言是一个极具挑战性的参数区域，尤其对于全 $f$ 模型更是如此。采用 $\delta f$ 方案的模拟结果与以往工作高度一致。混合变量/拉回方案在全 $f$ 与 $\delta f$ 两种情形下均展现出优异性能。采用混合方案（全 $f$ 高能粒子 + $\delta f$ 电子与热离子）的模拟表明，该新方案在降低噪声水平方面具有显著优势。全 $f$ 方案天然适用于高能粒子物理研究，可处理速度空间中高能粒子分布函数和剖面的大范围变化，为利用真实实验分布开展与间歇性和瞬态等离子体活动相关的动理学研究提供了强有力的工具。

全 $f$ 与 $\delta f$ 回旋动理学粒子模拟

I. 引言

回旋动理学粒子-网格（PIC）模拟为托卡马克等离子体研究提供了强有力的工具。${}^1$ 为提升模拟质量，特别是电磁模拟的质量，已发展了多种数值方案，例如平行动量 $p_{\parallel }$ 表达式、求解安培定律的迭代方案、${}^{2,3}$ 噪声矩阵方法${}^4$ 以及隐式方案。${}^{5,6}$ 最近已有综述全面总结了噪声抑制方案，${}^3$ 其中在 GYGLES 中使用单离子物种模型对线性物理开展了多种数值应用研究，结果表明控制变量法（control variate method）在降噪和提升模拟质量方面表现卓越。ORB5 程序中已实现了基于混合变量的拉回方案，并结合 $\delta f$ 方法用于高能粒子驱动 TAE 的研究，${}^7$ 展示了其在磁流体力学（MHD）极限下的能力。表 I 简要总结了部分前期工作中所采用的离散化方案（全 $f$、控制变量法或 $\delta f$）以及物理模型（“辛格式（$v_{\parallel }$）”、“哈密顿格式（$p_{\parallel }$）”或带拉回方案的混合变量）。

尽管大多数前期工作采用 $\delta f$ 方案，${}^8$ 近年来对全 $f$ 方法的研究投入了更多努力。${}^{5,9,10}$ 全 $f$ 方法不依赖于平衡态与扰动态的分离，因此能自然地处理模拟过程中剖面发生的显著变化。${}^9$ 然而，全 $f$ 模拟计算代价更高，且需要更严格的噪声抑制措施，才能使托卡马克等离子体的模拟研究切实可行。尤其是 MHD 极限下的全 $f$ 模型仍具挑战性。本文重点将噪声抑制方案应用于阿尔芬波与高能粒子物理的全 $f$ 与 $\delta f$ 模拟。遵循前期工作的理论框架，${}^3$ 我们在 TRIMEG-(GKX) 程序中实现了基于混合变量的拉回方案。${}^{5,11}$ TRIMEG（基于三角网格的回旋动理学程序）最初是为静电离子温度梯度模在整个等离子体区域的模拟而开发的，采用非结构化三角网格；${}^{11}$ 后来被扩展用于阿尔芬波与高能粒子物理研究，采用了全 $f$ 电磁模型。${}^5$ 下文中，全 $f$ 与 $\delta f$ 模型将在统一框架下进行公式化和实现。尽管 TRIMEG-(GKX) 程序中的全 $f$ 方案可应用于所有粒子种类，本文提出并应用了一种混合方案：高能粒子采用全 $f$，而热离子与电子采用 $\delta f$。实验中常见的一种现象是：速度空间中的高能粒子分布发生显著变化，而背景等离子体则很好地由麦克斯韦分布描述。借助这种新颖的混合全 $f$ 与 $\delta f$ 方案，可以自然地处理高能粒子剖面的大范围变化及其在速度空间中的任意分布，同时相比对所有粒子种类均采用全 $f$ 方案，计算性能也得到提升。得益于其面向对象编程及不同粒子种类的模块化设计，TRIMEG-(GKX) 程序已成功实现了针对不同粒子种类的混合方案。

本文结构如下：第二节推导了采用混合变量及拉回方案的全 $f$ 离散化方程；第三节给出了归一化方程并介绍了数值方法，其中包含一个严格推导的滤波器；第四节开展了高能粒子驱动的环向阿尔芬本征模（TAE）的 $\delta f$ 与全 $f$ 模拟，展示了各方案的特点，并讨论了托卡马克等离子体中高能粒子精确描述的关键问题。

II. 物理模型

A. 分布函数的离散化

沿用前期 $\delta f$ 工作中的公式化方法，${}^{3,12}$ 使用 $N$ 个标记粒子来表示给定分布：

$$g(z,t)\approx \sum _{p=1}^N\frac{\delta [z_p-z_p(t)]}{J_z},$$

其中 $z$ 为相空间坐标，$\delta$ 为狄拉克 delta 函数，$J_z$ 为对应的雅可比行列式，本文采用 $z=(\mathbf{R},v_{\parallel },\mu \equiv v_{\perp }^2/(2B))$，$\mathbf{R}$ 为实空间坐标。对于全 $f$ 模型，粒子的总分布由这些标记粒子表示，

$$f(z,t)=C_{g2f}{P}_{\mathrm{tot}}(z,t)g(z,t)\approx C_{g2f}\sum _{p=1}^N{p}_{p,\mathrm{tot}}(t)\frac{\delta \left[z_p-z_p(t)\right]}{J_z},$$

其中常数 $C_{g2f}\equiv N_f/N_g$，$N_{f/g}$ 表示粒子/标记的数量，$g$ 和 $f$ 分别表示标记和物理粒子。对于每个标记，

$$p_{p,\mathrm{tot}}(t)=\frac{1}{C_{g2f}}\frac{f(z_p,t)}{g(z_p,t)}=\mathrm{const},$$

完整的 $f$ 和 $\delta f$ 吉尔伯特-克鲁斯卡尔（GK）粒子模拟

适用于无碰撞等离子体，因为

$$\frac{\mathrm{d}g(z,t)}{\mathrm{d}t}=0,\frac{\mathrm{d}f(z,t)}{\mathrm{d}t}=0.$$

$P_{\mathrm{tot}}(z,t)$（以及相应的 $p_{p,\mathrm{tot}}$）的表达式可直接得到：

$$P_{\mathrm{tot}}(z,t)=\frac{1}{C_{g2f}}\frac{f(z,t)}{g(z,t)}=\frac{n_f}{⟨n_f{⟩}_V}\frac{⟨n_g{⟩}_V}{n_g}\frac{f_v}{g_v},$$

其中 $n_f$ 是密度分布，$f_v$ 是速度空间中的分布，即粒子分布函数 $f=n_f(\mathbf{R})f_v(v_{\parallel },\mu )$，$⟨\dots {⟩}_V$ 表示体积平均。如前所述，标记分布函数有多种选择。在本工作中，标记在环向方向和 $(R,Z)$ 平面内随机分布，但在速度空间中的分布与物理粒子相同，因此有

$$P_{\mathrm{tot}}(z,t)=\frac{n_f}{⟨n_f{⟩}_V}\frac{R}{R_0}.$$

密度和平行电流可直接由标记获得：

$$\begin{array}{rl}& \{n,j_{\parallel }{\}}^{i_r,i_{\theta },i_{\varphi }}\equiv \int \mathrm{d}V\{n,j_{\parallel }\}(\mathbf{R})N_{i_r}(r)N_{i_{\theta }}(\theta )N_{i_{\varphi }}(\varphi )\\ & =C_{g2f}\sum p_{p,\mathrm{tot}}\{1,v_{\parallel }\}{N}_{i_r}(r_p)N_{i_{\theta }}({\theta }_p)N_{i_{\varphi }}({\varphi }_p),\end{array}$$

其中对于一个假设的平衡态，体积元为 $\mathrm{d}V=rR\mathrm{d}r\mathrm{d}\theta \mathrm{d}\varphi$，$N_{i_r}$、$N_{i_{\theta }}$ 和 $N_{i_{\varphi }}$ 为基函数，$i_r$、$i_{\theta }$ 和 $i_{\varphi }$ 分别表示 $r$、$\theta$ 和 $\varphi$ 方向上的指标。

对于 $\delta f$ 模型，总分布函数被分解为背景部分和扰动部分：$f(z,t)=f_0(z,t)+\delta f(z,t)$。背景部分可选为不随时间变化的形式，即 $f_0(z,t)=f_0(z)$，典型的选择是麦克斯韦分布。背景分布函数和扰动分布函数通过标记表示如下：

$$f_0(z,t)=P(z,t)g(z,t)\approx \sum _{p=1}^N{p}_p(t)\frac{\delta [z_p-z_p(t)]}{J_z},$$

$$\delta f(z,t)=W(z,t)g(z,t)\approx \sum _{p=1}^N{w}_p(t)\frac{\delta [z_p-z_p(t)]}{J_z},$$

其中 $p_p(t)=f_0(z_p,t)/g(z_p,t)$ 和 $w_p(t)=\delta f(z_p,t)/g(z_p,t)$ 是随时间变化的变量。

完整的 $f$ 和 $\delta f$ 漂移回旋（GK）粒子模拟的演化方程可直接得到，${}^{12}$

$$\frac{\mathrm{d}}{\mathrm{d}t}{w}_p(t)=-p_p(t)\frac{\mathrm{d}}{\mathrm{d}t}\ln f_0(z_p(t)),$$

$$\frac{\mathrm{d}}{\mathrm{d}t}{p}_p(t)=p_p(t)\frac{\mathrm{d}}{\mathrm{d}t}\ln f_0(z_p(t)),$$

$$\frac{\mathrm{d}}{\mathrm{d}t}=\frac{\partial }{\partial t}+\dot{\mathbf{R}}\cdot \nabla +{\dot{v}}_{\parallel }\frac{\partial }{\partial v_{\parallel }},$$

其中在最后一个方程中使用了 $\dot{\mu }=0$。通常，导心运动方程可以分解为对应于平衡磁场的平衡部分和由扰动场引起的扰动部分：

$$\begin{array}{r}\dot{\mathbf{R}}={\dot{\mathbf{R}}}_0+\delta \dot{\mathbf{R}},\end{array}$$

$${\dot{v}}_{\parallel }={\dot{v}}_{\parallel ,0}+\delta {\dot{v}}_{\parallel }.$$

对于平衡分布函数，

$${\frac{\mathrm{d}}{\mathrm{d}t}|}_0{f}_0=\left[\frac{\partial }{\partial t}+{\dot{\mathbf{R}}}_0\cdot \nabla +{\dot{v}}_{\parallel ,0}\frac{\partial }{\partial v_{\parallel }}\right]f_0=0,$$

因此

$$\frac{\mathrm{d}}{\mathrm{d}t}{f}_0=\left[\delta \dot{\mathbf{R}}\cdot \nabla +\delta {\dot{v}}_{\parallel }\frac{\partial }{\partial v_{\parallel }}\right]f_0,$$

其中 $f_0$ 被选为定态解（即 $\partial f_0/\partial t=0$）。在本工作中，选择麦克斯韦分布（$f_0=f_{\mathrm{M}}$）。

$$f_{\mathrm{M}}=\frac{n_0}{(2T/m{)}^3{\pi }^{3/2}}\exp \left\{-\frac{m{v}_{\parallel }^2}{2T}-\frac{m\mu B}{T}\right\},$$

因此

$$\frac{\mathrm{d}}{\mathrm{d}t}\ln f_{\mathrm{M}}=\delta \dot{\mathbf{R}}\cdot \left[{\vec{\kappa }}_n+\left(\frac{m{v}_{\parallel }^2}{2T}+\frac{m\mu B}{T}-\frac{3}{2}\right){\vec{\kappa }}_T-\frac{m\mu B}{T}{\vec{\kappa }}_B\right]-\delta {\dot{v}}_{\parallel }\frac{m{v}_{\parallel }}{T},$$

其中 ${\vec{\kappa }}_{n,T,B}\equiv \nabla \ln \{n,T,B\}$。注意，对于麦克斯韦分布，在不考虑新经典物理的情况下，传统的 $\delta f$ 方案中采用了如下近似：

$${\frac{\mathrm{d}}{\mathrm{d}t}|}_0{f}_{\mathrm{M}}\approx 0.$$

全 $f$ 与 $\delta f$ 的陀螺动理学（GK）粒子模拟

	全 $f$	控制变量法	传统 $\delta f$
$v_{\parallel }$	5		6
$p_{\parallel }$		3	2,13
MV w/ PB	14, 本文工作	3	7, 本文工作

表 I. 使用全 $f$ 和 $\delta f$ 方案的各类研究。MV 和 PB 分别表示混合变量（Mixed Variable）和拉回（pullback）方案。

B. 使用混合变量的物理方程

混合变量定义如下。标量势的平行分量被分解为辛部分和哈密顿部分：

$$\delta A_{\parallel }=\delta A_{\parallel }^{\mathrm{s}}+\delta A_{\parallel }^{\mathrm{h}},$$

其中辛部分满足

$${\partial }_t\delta A_{\parallel }^{\mathrm{s}}+{\partial }_{\parallel }\delta \varphi =0.$$

导心的平行速度坐标定义为

$$u_{\parallel }=v_{\parallel }+\frac{q_s}{m_s}⟨\delta A_{\parallel }^{\mathrm{h}}⟩,$$

其中 $q_s$ 和 $m_s$ 分别为粒子种类 $s$ 的电荷与质量，下标 $s$ 表示不同的粒子种类，而 $⟨\dots ⟩$ 表示回旋平均。

导心运动方程与先前的工作一致：${}^{3,7,12}$

$$\begin{array}{rl}& \frac{\mathrm{d}{\mathbf{R}}_0}{\mathrm{d}t}=v_{\Vert }{\mathbf{b}}^{\ast }+\frac{m\mu }{q{B}^{\ast }}\mathbf{b}\times \nabla B,\\ & \frac{\mathrm{d}{u}_{\Vert ,0}}{\mathrm{d}t}=-\mu {\mathbf{b}}^{\ast }\cdot \nabla B,\\ & \frac{\mathrm{d}\delta \mathbf{R}}{\mathrm{d}t}=\frac{\mathbf{b}}{B^{\ast }}\times \nabla ⟨\delta \varphi -v_{\Vert }\delta A_{\Vert }⟩,\\ & \frac{\mathrm{d}\delta u_{\Vert }}{\mathrm{d}t}=-\frac{q_s}{m_s}\left({\mathbf{b}}^{\ast }\cdot \nabla ⟨\delta \varphi -v_{\Vert }\delta A_{\Vert }^{\mathrm{h}}⟩+{\partial }_t⟨\delta A_{\Vert }^{\mathrm{s}}⟩\right)-\frac{\mu }{B^{\ast }}\mathbf{b}\times \nabla B\cdot \nabla ⟨\delta A_{\Vert }^{\mathrm{s}}⟩,\end{array}$$

其中右侧采用的是 $v_{\parallel }$，因此在 $\mathrm{d}\mathbf{R}/\mathrm{d}t$ 中的项 $-(q_s/m_s)⟨\delta A_{\parallel }^{\mathrm{h}}⟩{\mathbf{b}}^{\ast }$ 已被计入 $\mathrm{d}{\mathbf{R}}_0/\mathrm{d}t$ 中。

准中性方程为

$$-\nabla \cdot \left(\sum _s\frac{q_s{n}_{0s}}{B{\omega }_{cs}}{\nabla }_{\perp }\delta \varphi \right)=\sum _s{q}_s\delta n_{s,v},$$

其中 $\delta n_s$ 由 $\delta f(\mathbf{R},v_{\parallel },\mu )$（记作 $\delta f_{s,v}$）计算得到，即 $\delta n_s(\mathbf{x})=\int {\mathrm{d}}^{6}z\delta f_s\delta (\mathbf{R}+\rho -\mathbf{x})$，${\omega }_{cs}$ 为种类 $s$ 的回旋频率；在本工作中，我们忽略了左侧的扰动电子极化密度。当采用 $\delta f$ 方案时，$\delta f_{s,v}$ 可通过 $\delta f_{s,u}$ 并结合拉回（pullback）方案的线性近似得到：

$$\delta f_v=\delta f_u+\frac{q_s⟨\delta A_{\Vert }^{\mathrm{h}}⟩}{m_s}\frac{\partial f_{0s}}{\partial v_{\Vert }}\stackrel{f_{0s}=f_{\mathrm{M}}}{\to }\delta f_u-\frac{m_s{v}_{\Vert }}{T_s}\frac{q_s⟨\delta A_{\Vert }^{\mathrm{h}}⟩}{m_s}{f}_{0s},$$

该式由更一般的形式推导而来：

$$\begin{array}{r}{f}_v(v_{\parallel })=f_u\left(v_{\parallel }+\frac{q_s}{m_s}⟨\delta A_{\parallel }^{\mathrm{h}}⟩\right).\end{array}$$

在 $v_{\parallel }$ 空间中的安培定律为

$$-{\nabla }_{\perp }^2\delta A_{\Vert }={\mu }_0\delta j_{\Vert ,v},$$

其中 $\delta j_{\parallel ,v}(\mathbf{x})=\int {\mathrm{d}}^{6}z\delta f_{v,s}\delta (\mathbf{R}+\rho -\mathbf{x})v_{\parallel }$。

对于 $\delta f$ 模型，采用混合变量并假设麦克斯韦分布，我们有

$$\begin{array}{rl}& \delta j_{\parallel ,v}\equiv \sum _s{q}_s\int \mathrm{d}{z}^6\delta f_s(v_{\parallel })\delta (\mathbf{R}+\rho -\mathbf{x})v_{\parallel }\\ & =\sum _s{q}_s\int \mathrm{d}{z}^6\left[\delta f_s(u_{\parallel })-\frac{v_{\parallel }{q}_s⟨\delta A_{\parallel }^{\mathrm{h}}⟩}{T_s}\right]\delta (\mathbf{R}+\rho -\mathbf{x})v_{\parallel }.\end{array}$$

于是我们可以将安培定律写为

$$\begin{array}{rl}& -{\nabla }_{\perp }^2\delta A_{\parallel }^{\mathrm{h}}+{\sum }_s{\mu }_0\frac{e_s^2}{T_s}\int \mathrm{d}{z}^6{v}_{\parallel }^2{f}_0⟨\delta A_{\parallel }^{\mathrm{h}}⟩\delta (\mathbf{R}+\rho -\mathbf{x})\\ & ={\nabla }_{\perp }^2\delta A_{\parallel }^{\mathrm{s}}+{\mu }_0{\sum }_s{q}_s\int \mathrm{d}{z}^6{v}_{\parallel }\delta f_s(u_{\parallel })\delta (\mathbf{R}+\rho -\mathbf{x}).\end{array}$$

左边的积分可以解析地求出，得到

$$\begin{array}{r}-{\nabla }_{\perp }^2\delta A_{\parallel }^{\mathrm{h}}+{\sum }_s\frac{1}{d_s^2}\overline{⟨\delta A_{\parallel }^{\mathrm{h}}⟩}={\nabla }_{\perp }^2\delta A_{\parallel }^{\mathrm{s}}\\ +{\mu }_0{\sum }_s{q}_s\int \mathrm{d}{z}^6{v}_{\parallel }\delta f_s(u_{\parallel })\delta (\mathbf{R}+\rho -\mathbf{x}),\end{array}$$

其中

$$\overline{⟨\delta A_{\parallel }^{\mathrm{h}}⟩}\equiv \frac{2}{n_{s0}{v}_{ts}}\int \mathrm{d}{z}^6{v}_{\parallel }^2{f}_0⟨\delta A_{\parallel }^{\mathrm{h}}⟩\delta (\mathbf{R}+\rho -\mathbf{x}),$$

这里 $v_{\mathrm{ts}}=\sqrt{2T_s/m_s}$，$d_s$ 是物种 $s$ 的趋肤深度，定义为 $d_s^2=c^2/{\omega }_{p,s}^2=m_s/({\mu }_0{q}_s^2{n}_{0s})$。

---

全 $f$ 与 $\delta f$ 的GK粒子模拟

对于全 $f$ 模型，扰动电流由全 $f$ 表示：

$$\delta j_{\parallel ,v}=\sum _s{q}_s\int \mathrm{d}{v}^3{v}_{\parallel }{f}_s=\sum _s{q}_s\int \mathrm{d}{z}^6\left[u_{\parallel }-\frac{q_s}{m_s}⟨\delta A_{\parallel }^{\mathrm{h}}⟩\right]f_s\delta (\mathbf{R}+\rho -\mathbf{x}).$$

安培定律给出

$$\begin{array}{rl}& -{\nabla }_{\perp }^2\delta A_{\parallel }^{\mathrm{h}}+{\sum }_s{\mu }_0\frac{e_s^2}{m_s}\int \mathrm{d}{z}^6{f}_s⟨\delta A_{\parallel }^{\mathrm{h}}⟩\delta (\mathbf{R}+\rho -\mathbf{x})\\ & ={\nabla }_{\perp }^2\delta A_{\parallel }^{\mathrm{s}}+{\mu }_0{\sum }_s{q}_s\int \mathrm{d}{z}^6{u}_{\parallel }{f}_s\delta (\mathbf{R}+\rho -\mathbf{x}).\end{array}$$

相应的解析极限形式与式(30)类似，只需将 $\delta f(u_{\parallel })$ 替换为 $f(u_{\parallel })$，并重新定义 $⟨\delta A_{\parallel }^{\mathrm{h}}⟩$：

$$\begin{array}{r}-{\nabla }_{\perp }^2\delta A_{\parallel }^{\mathrm{h}}+{\sum }_s\frac{1}{d_s^2}\overline{⟨\delta A_{\parallel }^{\mathrm{h}}⟩}={\nabla }_{\perp }^2\delta A_{\parallel }^{\mathrm{s}}\\ +{\mu }_0{\sum }_s{q}_s\int \mathrm{d}{z}^6{v}_{\parallel }{f}_s(u_{\parallel })\delta (\mathbf{R}+\rho -\mathbf{x}),\end{array}$$

其中

$$⟨\delta A_{\parallel }^{\mathrm{h}}⟩\equiv \frac{1}{n_{s0}}\int \mathrm{d}{z}^6{f}_0⟨\delta A_{\parallel }^{\mathrm{h}}⟩\delta (\mathbf{R}+\rho -\mathbf{x}).$$

利用迭代格式，渐近解可表示如下：

$$\delta A_{\Vert }^{\mathrm{h}}=\sum _{p=0}^{\infty }\delta A_{\Vert ,p}^{\mathrm{h}},$$

其中 $ϵ=|\delta A_{\parallel ,p+1}^{\mathrm{h}}/\delta A_{\parallel ,p}^{\mathrm{h}}|\ll 1$。安培定律按阶次逐级求解：

$$\left({\nabla }_{\perp }^2-\sum _s\frac{1}{d_s^2}\right)\delta A_{\Vert ,0}^{\mathrm{h}}=-{\nabla }_{\perp }^2\delta A_{\Vert }^{\mathrm{s}}-{\mu }_0\delta j_{\Vert ,p},$$

$$\left({\nabla }_{\perp }^2-\sum _s\frac{1}{d_s^2}\right)\delta A_{\Vert ,p}^{\mathrm{h}}=-\sum _s\frac{1}{d_s^2}\delta A_{\Vert ,p-1}^{\mathrm{h}}+\sum _s\frac{1}{d_s^2}⟨\delta A_{\Vert ,p-1}^{\mathrm{h}}⟩,$$

$$\overline{⟨\delta A_{\Vert ,p-1}^{\mathrm{h}}⟩}=\frac{2}{n_0{v}_{\mathrm{ts}}^2}\int \mathrm{d}{z}^6{v}_{\Vert }^2{f}_0⟨\delta A_{\Vert ,p-1}^{\mathrm{h}}⟩\delta (\mathbf{R}+\rho -\mathbf{x}),\mathrm{for}\delta f\mathrm{model}$$

$$\overline{⟨\delta A_{\parallel ,p-1}^{\mathrm{h}}⟩}=\frac{1}{n_0}\int \mathrm{d}{z}^{6}f⟨\delta A_{\parallel ,p-1}^{\mathrm{h}}⟩\delta (\mathbf{R}+\rho -\mathbf{x}),\mathrm{for}\mathrm{full}f\mathrm{model}$$

其中 $p=1,2,3,\dots$，并且由于在解析极限下对于麦克斯韦分布有 $2/(n_0{v}_{\mathrm{ts}}^2)\int \mathrm{d}{v}^3{v}_{\parallel }^2{f}_0=1$ 和 $(1/n_0)\int \mathrm{d}{v}^3{v}_{\parallel }^2{f}_0=1$，因此预期迭代求解器具有良好的收敛性。

完整的 $f$ 和 $\delta f$ 吉拉德-金斯（GK）粒子模拟

C. 用于缓解抵消问题的回拉（pullback）方案

关于回拉方案的更详细描述可参见先前的工作。${}^7$ 作为简要回顾，$\delta f$ 的方程如下所示：

$$\delta A_{\parallel ,\mathrm{new}}^{\mathrm{s}}=\delta A_{\parallel ,\mathrm{old}}^{\mathrm{s}}+\delta A_{\parallel ,\mathrm{old}}^{\mathrm{h}},$$

$$u_{\parallel ,\mathrm{new}}=u_{\parallel ,\mathrm{old}}-\frac{q_s}{m_s}⟨\delta A_{\parallel ,\mathrm{old}}^{\mathrm{h}}⟩,$$

$$\delta f_{\mathrm{new}}=\delta f_{\mathrm{old}}+\frac{q_s⟨\delta A_{\parallel ,\mathrm{old}}^{\mathrm{h}}⟩}{m_s}\frac{\partial f_{0s}}{\partial v_{\parallel }}\frac{\mathrm{Maxwellian}}{f_{0s}=f_M}\frac{\partial f_{\mathrm{old}}}{\partial v_{\mathrm{ts}}^2}\frac{q_s⟨\delta A_{\parallel ,\mathrm{old}}^{\mathrm{h}}⟩}{m_s}{f}_{0s},$$

其中式（43）是 $\delta f$ 回拉的线性化方程，它来源于分布函数变换的一般方程：

$$f_{\mathrm{old}}(u_{\Vert \mathrm{old}})=f_{\mathrm{new}}(u_{\Vert \mathrm{new}}=u_{\Vert \mathrm{old}}-\frac{q_s}{m_s}⟨\delta A_{\Vert ,\mathrm{old}}^{\mathrm{h}}⟩).$$

对于全 $f$ 方案，仅需使用方程 (41) 和 (42)。

D. 不变量坐标下的动力学平衡

尽管局域麦克斯韦分布被广泛应用于回旋动理学模拟中，但在全 $f$ 方案中使用该分布会引入标记粒子弛豫效应，从而导致由高能粒子（EP）驱动的TAE问题的增长率降低。在 $\delta f$ 粒子程序 ORB5 中，已采用平移后的环向正则动量进行湍流研究${}^{15}$。本文将该方案也应用于全 $f$ 模型中。为在不变量空间中构建标记粒子分布，我们采用平移后的环向正则动量：

$${\psi }_{\mathrm{can}}=\psi +\frac{m_{s}F}{q_{s}B}{v}_{\parallel }-\mathrm{sign}(v_{\parallel })\sqrt{2(E-\mu B_0)}\frac{mF}{q{B}_0}H(E-\mu B_0),$$

其中最后一项给出了有限轨道宽度的大小。对于高能粒子，在方程 (45) 右侧各项中，第二项的量级可与第一项相当，因此自然地引入该平移项（即最后一项），使得 ${\psi }_{\mathrm{can}}$ 接近轨道中心。分布函数设定为：

$$f_{\mathrm{can}}({\psi }_{\mathrm{can}},E,\mu )=n({\psi }_{\mathrm{can}})\exp \left\{-\frac{mE}{T({\psi }_{\mathrm{can}})}\right\},$$

为简化起见，此处忽略了沿 $\mu$ 方向的变化。相应地，在加载标记粒子时，方程 (5) 中的 $n(r)$ 被替换为 $n(r_{\mathrm{can}})$，其中 $r_{\mathrm{can}}^2\equiv ({\psi }_{\mathrm{can}}-{\psi }_{\mathrm{axis}})/({\psi }_{\mathrm{edge}}-{\psi }_{\mathrm{axis}})$，当 $({\psi }_{\mathrm{can}}-{\psi }_{\mathrm{axis}})/({\psi }_{\mathrm{edge}}-{\psi }_{\mathrm{axis}})\ge 0$ 时，$r_{\mathrm{can}}\ge 0$；当 $({\psi }_{\mathrm{can}}-{\psi }_{\mathrm{axis}})/({\psi }_{\mathrm{edge}}-{\psi }_{\mathrm{axis}})<0$ 时，$r_{\mathrm{can}}<0$。

全 $f$ 与 $\delta f$ 回旋动理学粒子模拟

III. 数值方案

A. 无量纲化方程

本节介绍 TRIMEG-GKX 程序中变量的无量纲化方法。长度单位取为 $R_{\mathrm{N}}=1$ m。粒子质量以 $m_{\mathrm{N}}$ 为单位进行归一化，并取 $m_{\mathrm{N}}=m_{\mathrm{e}}$。速度单位为

$$v_{\mathrm{N}}\equiv \sqrt{2T_{\mathrm{N}}/m_{\mathrm{N}}},$$

其中 $T_{\mathrm{N}}$ 和 $m_{\mathrm{N}}$ 分别为用于归一化的温度和质量单位。

温度以 $T_{\mathrm{N}}=m_{\mathrm{N}}{v}_{\mathrm{N}}^2/2$ 为单位进行归一化，即

$$T_s={\bar{T}}_s{T}_{\mathrm{N}}=\frac{1}{2}{\bar{T}}_s{m}_{\mathrm{N}}{v}_{\mathrm{N}}^2.$$

注意另一种方法（本文未采用）是将温度 $T$ 归一化为 $2T_{\mathrm{N}}$，即 $T_s=T_s{m}_{\mathrm{N}}{v}_{\mathrm{N}}^2=2{\bar{T}}_s{T}_{\mathrm{N}}$。此外，$\mu$ 被归一化为 $v_{\mathrm{N}}^2/B_{\mathrm{ref}}$，

$$\mu \equiv \frac{v_{\perp }^2}{2B}=\bar{\mu }\frac{v_{\mathrm{N}}^2}{B_{\mathrm{ref}}},$$

其中 $B_{\mathrm{ref}}=1$ T。

麦克斯韦分布为

$$f_{\mathrm{M}}=\frac{1}{v_{\mathrm{t}}^3{\pi }^{3/2}}{e}^{-\frac{m{v}_{\parallel }^2+2\mu B}{2T}}=\frac{1}{v_{\mathrm{t}}^3{\pi }^{3/2}}\exp \left\{-\frac{\bar{m}{\bar{v}}_{\parallel }^2}{\bar{T}}-2\frac{\bar{m}\bar{\mu }}{\bar{T}}\frac{B}{B_{\mathrm{ref}}}\right\},$$

相应地，

$$\begin{array}{rl}& \frac{\mathrm{d}}{\mathrm{d}t}\ln f_{\mathrm{M}}=\frac{\mathrm{d}\delta \bar{\mathbf{R}}}{\mathrm{d}\bar{t}}\cdot \left[{\vec{\kappa }}_n+\left(\frac{\bar{m}{\bar{v}}_{\parallel }^2}{\bar{T}}+\frac{2\bar{m}\bar{\mu }\bar{B}}{\bar{T}}-\frac{3}{2}\right){\vec{\kappa }}_T-2\frac{\bar{m}\bar{\mu }\bar{B}}{\bar{T}}{\vec{\kappa }}_B\right]\\ & -\frac{2\bar{m}{\bar{v}}_{\parallel }}{\bar{T}}\frac{\mathrm{d}\delta {\bar{v}}_{\parallel }}{\mathrm{d}\bar{t}}.\end{array}$$

在速度空间中，标记粒子与物理粒子具有相同的分布，但在极向平面和环向方向上均匀分布。在 $v_{\parallel }$ 方向上，使用随机数生成器产生服从正态分布 $f(x)=1/(\sigma \sqrt{2\pi })\exp \{-[(x-x_0)/\sigma {]}^2/2\}$ 的数值，其中 $x_0$ 和 $\sigma$ 分别取为 0 和 $\sqrt{\bar{T}/(2\bar{m})}$。在 $\mu$ 方向上，生成均匀分布的随机数 $x$，并按 $\mu =-\ln (x)\bar{T}{B}_{\mathrm{ref}}/(2\bar{m}B)$ 进行变换。

全 $f$ 与 $\delta f$ 陀螺动理学粒子模拟

归一化的导心运动方程为

$$\frac{\mathrm{d}{\mathbf{R}}_0}{\mathrm{d}t}=v_{\parallel }{\mathbf{b}}^{\ast }+\frac{{\bar{m}}_s}{q_s}{\bar{\rho }}_{\mathrm{N}}\frac{B_{\mathrm{ref}}}{B^2{B}^{\ast }}\mu \mathbf{B}\times \nabla B,$$

$$\frac{\mathrm{d}{u}_{\parallel ,0}}{\mathrm{d}t}=-\mu {\mathbf{b}}^{\ast }\cdot \nabla B,$$

$$\frac{\mathrm{d}\delta \mathbf{R}}{\mathrm{d}t}={\bar{\rho }}_{\mathrm{N}}\frac{B_{\mathrm{ref}}}{B^{\ast }}\mathbf{b}\times \nabla ⟨\delta \varphi -v_{\parallel }\delta A_{\parallel }⟩,$$

$$\begin{array}{r}\frac{\mathrm{d}\delta u_{\parallel }}{\mathrm{d}t}=-\frac{{\bar{q}}_s}{{\bar{m}}_s}\left({\mathbf{b}}^{\ast }\cdot \nabla ⟨\delta \varphi -v_{\parallel }\delta A_{\parallel }^{\mathrm{h}}⟩+{\partial }_t⟨\delta A_{\parallel }^{\mathrm{s}}⟩\right)\\ -{\rho }_{\mathrm{N}}\frac{B_{\mathrm{ref}}}{B^{\ast }}\mu \mathbf{b}\times \nabla B\cdot \nabla ⟨\delta A_{\parallel }^{\mathrm{s}}⟩,\end{array}$$

其中 $\delta \varphi$ 和 $\delta A_{\parallel }$ 分别归一化为 $m_{\mathrm{N}}{v}_{\mathrm{N}}^2/e$ 和 $m_{\mathrm{N}}{v}_{\mathrm{N}}/e$。

归一化的准中性方程为：

$${\nabla }_{\perp }\sum n_{0s}{\bar{M}}_s(B_{\mathrm{axis}}/B{)}^2{\nabla }_{\perp }\delta \bar{\varphi }=C_{\mathrm{P}}\sum (-{\bar{e}}_s)\delta n_s,$$

其中 $C_{\mathrm{P}}=1/{\rho }_{\mathrm{N}}^2$。

对于安培定律，原始的归一化方程 ${\nabla }_{\perp }^2\delta A=C_{\mathrm{A}}\delta J_{\parallel ,\mathrm{ph}}$（其中 $C_{\mathrm{A}}={\beta }_{\mathrm{ref}}/{\rho }_N^2$）通过混合变量和迭代格式求解（对应于公式 37–40）：

$$\left({\nabla }_{\perp }^2-\sum _s\frac{{\vec{q}}_s^2}{M_s}{C}_{\mathrm{A}}\right)\delta A_{\parallel ,0}^{\mathrm{h}}=-{\nabla }_{\perp }^2\delta A_{\parallel ,0}^{\mathrm{s}}-C_{\mathrm{A}}\delta J_{\parallel },$$

$$\left({\nabla }_{\perp }^2-\sum _s\frac{{\bar{q}}_s^2}{M_s}{C}_{\mathrm{A}}\right)\delta A_{\parallel ,0}^{\mathrm{h}}=-\sum _s\frac{{\bar{q}}_s^2}{M_s}{C}_{\mathrm{A}}\delta A_{\parallel ,p-1}^{\mathrm{h}}+\bar{G}\delta A_{\parallel ,p-1}^{\mathrm{h}}$$

$$\bar{G}\delta A_{\parallel ,p-1}^{\mathrm{h}}=C_{\mathrm{A}}\frac{N_{0s}{\bar{q}}_s^2}{T_s}\sum _{p}2v_{\parallel ,p}^2\int d{z}^6{w}_p\delta (\mathbf{R}+\rho -\mathbf{x})⟨\delta A_{\parallel ,p-1}^{\mathrm{h}}⟩\text{for}\delta f,$$

$$\bar{G}\delta A_{\parallel ,p-1}^{\mathrm{h}}=C_{\mathrm{A}}\frac{N_{0s}{\bar{q}}_s^2}{M_s}\sum _p\int d{z}^6{p}_{p,\mathrm{tot}}\delta (\mathbf{R}+\rho -\mathbf{x})⟨\delta A_{\parallel ,p-1}^{\mathrm{h}}⟩\text{for full}f.$$

拉回（pullback）处理的归一化方程如下：

$$\delta A_{\parallel ,\mathrm{new}}^{\mathrm{s}}=\delta A_{\parallel ,\mathrm{old}}^{\mathrm{s}}+\delta A_{\parallel ,\mathrm{old}}^{\mathrm{h}},$$

$$u_{\parallel ,\mathrm{new}}=u_{\parallel ,\mathrm{old}}-\frac{\bar{q}}{{\bar{m}}_s}⟨\delta A_{\parallel ,\mathrm{old}}^{\mathrm{h}}⟩,$$

$$\delta f_{\mathrm{new}}=\delta f_{\mathrm{old}}+\frac{{\bar{q}}_s⟨\delta A_{\parallel ,\mathrm{old}}^{\mathrm{h}}⟩}{{\bar{m}}_s}\frac{\partial f_{0s}}{\partial {\bar{v}}_{\parallel }}$$

$$\frac{\mathrm{Maxwellian}}{f_{0s}=f_{\mathrm{M}}}\to \delta f_{\mathrm{old}}-\frac{2{\bar{q}}_s}{T_s}{\bar{v}}_{\parallel }⟨\delta A_{\parallel ,\mathrm{old}}^{\mathrm{h}}⟩f_{0s},$$

其中因子 2 来源于温度 $T$ 归一化到 $T_{\mathrm{N}}=m_{\mathrm{N}}{v}_{\mathrm{N}}^2/2$。式 (62) 是本文工作中实现的 $\delta f$ 模型的线性化拉回格式。使用非线性拉回格式的研究超出了本文的范围，将在未来工作中讨论。

B. 有限元方法

本文开发了一个三维求解器，在径向、极向和环向均采用有限元方法。极向和环向采用周期性边界条件；在径向则施加函数值为零的 Dirichlet 边界条件。网格尺寸为 $(N_r,N_{\theta },N_{\varphi })$，并在模拟域中采用 $(N_{r,\text{FEM}},N_{\theta ,\text{FEM}},N_{\varphi ,\text{FEM}})$ 个基函数来表示函数，其中 $N_{r,\text{FEM}}=N_r+\Delta N$，$N_{\theta ,\text{FEM}}=N_{\theta }$，$N_{\varphi ,\text{FEM}}=N_{\varphi }$，这些设置与边界条件一致。由于采用了三次样条，故 $\Delta N=2$。

在极向和环向，三次有限元基函数 $N(x)$ 定义如下：

$$N_{\mathrm{cubic}}(x)=\{\begin{array}{ll}4/3+2x+x^2+x^3/6,& \mathrm{if}x\in [-2,-1)\\ 2/3-x^2-x^3/2,& \mathrm{if}x\in [-1,0)\\ 2/3-x^2+x^3/2,& \mathrm{if}x\in [0,1)\\ 4/3-2x+x^2-x^3/6.& \mathrm{if}x\in [1,2)\end{array}$$

沿 $\theta$ 和 $\varphi$ 方向，第 $i$ 个基函数为 $N_i=N_{\mathrm{cubic}}(x+1-i)$。在径向方向，当 $i\ge 4$ 或 $i\le N_{r,\mathrm{FEM}}-3$ 时，$N_i$ 与极向/环向的基函数形式相同。第一个基函数为：

$$N_{\mathrm{cubic}}(x)=\{\begin{array}{ll}0,& \mathrm{if}x\in [-2,1)\\ -x^3+6x^2-12x+8.& \mathrm{if}x\in [1,2)\end{array}$$

第二个基函数为：

$$N_{\mathrm{cubic}}(x)=\{\begin{array}{ll}0,& \mathrm{if}x\in [-2,0)\\ 7x^3/6-3x^2+2x,& \mathrm{if}x\in [0,1)\\ 4/3-2x+x^2-x^3/6.& \mathrm{if}x\in [1,2)\end{array}$$

全 $f$ 与 $\delta f$ GK 粒子模拟

第三个基函数为：

$$N_{\mathrm{cubic}}(x)=\{\begin{array}{ll}0,& \mathrm{if}x\in [-2,-1)\\ -x^3/3-x^2+2/3,& \mathrm{if}x\in [-1,0)\\ x^3/2-x^2+2/3,& \mathrm{if}x\in [0,1)\\ -x^3/6+x^2-2x+4/3.& \mathrm{if}x\in [1,2)\end{array}$$

最后三个基函数是前三个基函数关于模拟域中点的对称映射。所有径向基函数均按 $N_i=N_{\text{cubic}}(x+1-i)$ 构造，其中 $i\in [1,N_{r,\text{FEM}}]$。

C. 场方程的弱形式

对于偏微分方程

$$L(r,\theta ,\varphi )y(r,\theta ,\varphi )=b(r,\theta ,\varphi ),$$

其中 $L$ 为线性微分算子，其弱形式可写为

$$\begin{array}{rl}& \int \mathrm{d}r\mathrm{d}\theta \mathrm{d}\varphi S(r,\theta ,\varphi )N_{i_r}{N}_{i_{\theta }}{N}_{i_{\varphi }}L(r,\theta ,\varphi )y(r,\theta ,\varphi )\\ & =\int \mathrm{d}r\mathrm{d}\theta \mathrm{d}\varphi S(r,\theta ,\varphi )N_{i_r}{N}_{i_{\theta }}{N}_{i_{\varphi }}b(r,\theta ,\varphi ).\end{array}$$

其中 $S(r,\theta ,\varphi )$ 是一个函数，本文中取 $S=1$。准中性方程、安培定律、迭代方程和欧姆定律的弱形式分别为：

$${\overline{\stackrel{ˉ}{M}}}_{P,L;i{i}^{\prime },j{j}^{\prime },k{k}^{\prime }}\cdot \delta {\varphi }_{i^{\prime }{j}^{\prime }{k}^{\prime }}=C_{\mathrm{P}}\delta N^{i,j,k},$$

$${\bar{\mathcal{M}}}_{\mathrm{A},L,i{i}^{\prime },j{j}^{\prime },k{k}^{\prime }}\cdot \delta A_{i^{\prime }{j}^{\prime }{k}^{\prime }}^{\mathrm{h}}={\bar{\mathcal{M}}}_{\mathrm{A},R,i{i}^{\prime },j{j}^{\prime },k{k}^{\prime }}\delta A_{i^{\prime }{j}^{\prime }{k}^{\prime }}^{\mathrm{s}}+C_{\mathrm{A}}\delta J^{i,j,k},$$

$${\overline{\stackrel{ˉ}{M}}}_{\mathrm{it},L,i{i}^{\prime },j{j}^{\prime },k{k}^{\prime }}\cdot \delta A_{i^{\prime }{j}^{\prime }{k}^{\prime },[p+1]}^h={\overline{\stackrel{ˉ}{M}}}_{\mathrm{it},R,i{i}^{\prime },j{j}^{\prime },k{k}^{\prime }}\cdot \delta A_{i^{\prime }{j}^{\prime }{k}^{\prime },[p]}^h+⟨\delta A^{h,i^{\prime }{j}^{\prime }{k}^{\prime },[p]}⟩,$$

$${\overline{\stackrel{ˉ}{M}}}_{\mathrm{Ohm},L,i{i}^{\prime },j{j}^{\prime },k{k}^{\prime }}\cdot \delta A_{i^{\prime }{j}^{\prime }{k}^{\prime }}^s={\overline{\stackrel{ˉ}{M}}}_{\mathrm{Ohm},R,i{i}^{\prime },j{j}^{\prime },k{k}^{\prime }}\cdot \delta {\varphi }_{i^{\prime }{j}^{\prime }{k}^{\prime }}$$

全 $f$ 和 $\delta f$ 的陀螺动理学（GK）粒子模拟

D. 傅里叶滤波

1. 矩量的滤波（粒子-傅里叶方法）

对于矩量变量（$\delta n$ 和 $\delta j_{\parallel }$），首先从标记粒子计算其傅里叶分量如下：

$$\{\delta n_{n,m},\delta j_{\Vert ,n,m}\}=C_{p2g}\sum _p\{1,v_{\Vert }\}{w}_p{e}^{-in{\varphi }_p-\mathrm{i}m{\theta }_p},$$

其中 $n$ 和 $m$ 分别为滤波器的环向和极向模数，$C_{p2g}$ 是将标记粒子变量转换为网格变量的转换因子。相应的样条系数可直接得到：

$$\{\delta n,\delta j_{\parallel }{\}}_{i_r,i_{\theta },i_{\varphi }}=\{\delta n,\delta j_{\parallel }{\}}_{n,m}{T}_{n,i_{\varphi }}{T}_{m,i_{\theta }},$$

其中

$$T_{n,i}={\int }_{{\varphi }_{\min }}^{{\varphi }_{\max }}\mathrm{d}\varphi e^{\mathrm{i}n\varphi }{N}_i(\varphi )=\Delta \varphi {\int }_{-2}^2\mathrm{d}x{e}^{\mathrm{i}{n}_{\mathrm{eff}}x}{N}_i(x),$$

$$T_{m,i}={\int }_{{\theta }_{\min }}^{{\theta }_{\max }}\mathrm{d}\theta e^{\mathrm{i}m\theta }{N}_i(\theta )=\Delta \theta {\int }_{-2}^2\mathrm{d}x{e}^{\mathrm{i}{m}_{\mathrm{eff}}x}{N}_i(x).$$

其中 $n_{\mathrm{eff}}=n\Delta \varphi$，$m_{\mathrm{eff}}=n\Delta \theta$，$\Delta \varphi$ 和 $\Delta \theta$ 分别为环向和极向的网格尺寸。解析结果用于构造如下公式：

$${\int }_{-2}^2\mathrm{d}xN(x)e^{-inx}=\frac{6+2\cos (2n)-8\cos (n)}{n^4}.$$

2. 场量滤波

对于场变量（如 $\delta \varphi$ 和 $\delta A_{\parallel }$），其物理值通过样条系数表示，并对这些物理值应用傅里叶滤波。变量 $\delta \varphi$ 的样条系数在 $\varphi$ 和 $\theta$ 方向上的滤波方式如下：

$$\delta {\bar{\varphi }}_{i_{\varphi }}=2\mathrm{Re}\left\{M_{i_{\varphi }{j}_{\varphi }}^{-1}\left[T_{n,i_{\varphi }}{T}_{-n,j_{\varphi }}\delta {\varphi }_{j_{\varphi }}\right]/{\varphi }_{\mathrm{wid}}\right\},$$

$$\delta {\bar{\varphi }}_{i_{\theta }}=2\mathrm{Re}\left\{M_{i_{\theta }{j}_{\theta }}^{-1}\left[T_{m,i_{\theta }}{T}_{-m,j_{\theta }}\delta {\varphi }_{j_{\theta }}\right]/{\theta }_{\mathrm{wid}}\right\},$$

其中 ${\varphi }_{\mathrm{wid}}$ 和 ${\theta }_{\mathrm{wid}}$ 分别为环向和极向模拟区域的宽度；对于全环模拟，${\varphi }_{\mathrm{wid}}=2\pi$，${\theta }_{\mathrm{wid}}=2\pi$；$M_{i,j}$ 为质量矩阵。

全 $f$ 与 $\delta f$ 吉尔伯特-金斯（GK）粒子模拟

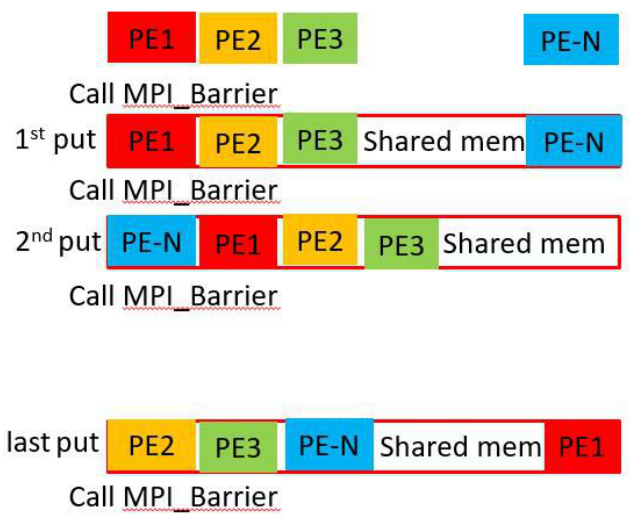
图 1. 标记粒子向共享内存中场变量投影的示意图。

E. 并行化及共享内存 MPI 在场量实现中的应用

标记粒子分布于所有进程并在各进程中独立推进（粒子分解），而每个进程均可访问完整的场变量集合（无区域分解）。场变量存储于每个计算节点的共享内存中，该机制由 MPI-3 标准支持。这一设计主要出于全 $f$ 模拟的需求：此时标记粒子数量庞大，计算开销主要集中于粒子部分。此外，采用混合变量与回拉（pullback）格式所允许的时间步长（$\Delta t\sim T_{\text{TAE}}/20$）显著大于传统的纯 $p_{\parallel }$ 形式；同时，大量标记粒子可能沿磁力线迁移，若采用区域分解将导致显著的通信开销。然而，场方程通过 PETSc 求解，场求解器已完全并行化。尽管 MPI-3 支持共享内存上的原子操作（如 "MPI_ACCUMULATE"），但此类操作在标记-场投影中的通信效率仍较低。因此，TRIMEG-GKX 中的投影操作通过将标记粒子按其需写入的内存区域进行分箱处理来实现，如图 1 所示。由于计算开销主要来自于在标记位置计算基函数值，判断是否轮到向内存写入数据所带来的额外开销可忽略不计。

全 $f$ 与 $\delta f$ GK 粒子模拟

IV. 模拟设置与结果

本工作利用 ITPA 小组定义的参数模拟了由高能粒子驱动的环向阿尔芬本征模（TAE）。主要参数如下：大半径 $R_0=10$ m，小半径 $a=1$ m，轴上磁场 $B_0=3$ T，安全因子剖面 $q(r)=1.71+0.16r^2$。电子密度恒定，$n_{\mathrm{e}0}=2.0\times 10^{19}$ m${}^{-3}$，电子温度 $T_{\mathrm{e}}=1$ keV。电子压强与磁压强之比为 ${\beta }_{\mathrm{e}}\approx 9\times 10^{-4}$。热离子的拉莫尔半径为 ${\rho }_{\mathrm{ti}}=c{m}_{\mathrm{i}}{v}_{\mathrm{ti}}/(e{B}_{\mathrm{axis}})=0.00152$ m。安培方程左侧绝热项 $(\delta A_{\mathrm{h}}/d_{\mathrm{e}}^2)$ 与非绝热项 $({\nabla }_{\perp }^2\delta A^{\mathrm{h}})$ 之比为 $1/(d_{\mathrm{e}}^2{k}_{\perp }^2)\approx {\beta }_{\mathrm{e}}/(k_{\perp }{\rho }_{\mathrm{ti}}{)}^2\ast (m_{\mathrm{i}}{T}_{\mathrm{i}}/m_{\mathrm{e}}{T}_{\mathrm{e}})\approx 1.622\times 10^3$，其中 $k_{\perp }\approx nq/r=6\times 1.75/0.5=21$。该 ITPA-TAE 算例具有较小的电子惯性长度（$d_{\mathrm{e}}\approx 1.182\times 10^{-3}$ m），若不采用回拉格式，则会遭遇“抵消问题”（cancellation problem）。

EP 密度分布由下式给出：

$$\begin{array}{r}{n}_{\mathrm{EP}}(r)=n_{\mathrm{EP},0}{c}_3\exp \left(-\frac{c_2}{c_1}\tanh \frac{r-c_0}{c_2}\right),\\ \frac{\mathrm{d}\ln n_{\mathrm{EP}}}{\mathrm{d}r}=-\frac{1}{c_1}\left[1-{\tanh }^2\frac{r-c_0}{c_2}\right]\end{array}$$

其中 $n_{\mathrm{EP},0}=1.44131\times 10^{17}{\mathrm{m}}^{-3}$，下标“EP”表示高能粒子（energetic particles），$c_0=0.49123$，$c_1=0.298228$，$c_2=0.198739$，$c_3=0.521298$。基准情形下的 EP 温度为 400 keV。

A. 数值验证

以 EP 驱动的 TAE 基准情形（$T_{\mathrm{EP}}=400$ keV）进行收敛性研究。首先，我们需要确定时间步长，并了解其在后续研究中的最大可接受值。本文中模拟的是 $n=6$ 的 TAE，环向方向仅取整个环面的 $1/6$。由于每个波长使用 8 个网格点已足够，因此取 $N_{\varphi }=8$。由于频率主要由非共振粒子决定，而增长率主要由共振 EP 决定，因此增长率通常需要更高的分辨率，我们仅展示增长率的收敛性。对于典型的网格规模 $(N_r,N_{\theta },N_{\varphi })=(64,128,8)$，每种粒子种类选取的标记粒子数为 $N_{\mathrm{marker}}=4\times 10^5$。不同时间步长对应的增长率如图 2 左图所示。当 $\Delta t/T_{\mathrm{A}}\le 0.05$ 时，增长率开始收敛，其中 $T_{\mathrm{A}}$ 是在 $r_{\mathrm{c}}=0.5$ 处估算的 TAE 周期，

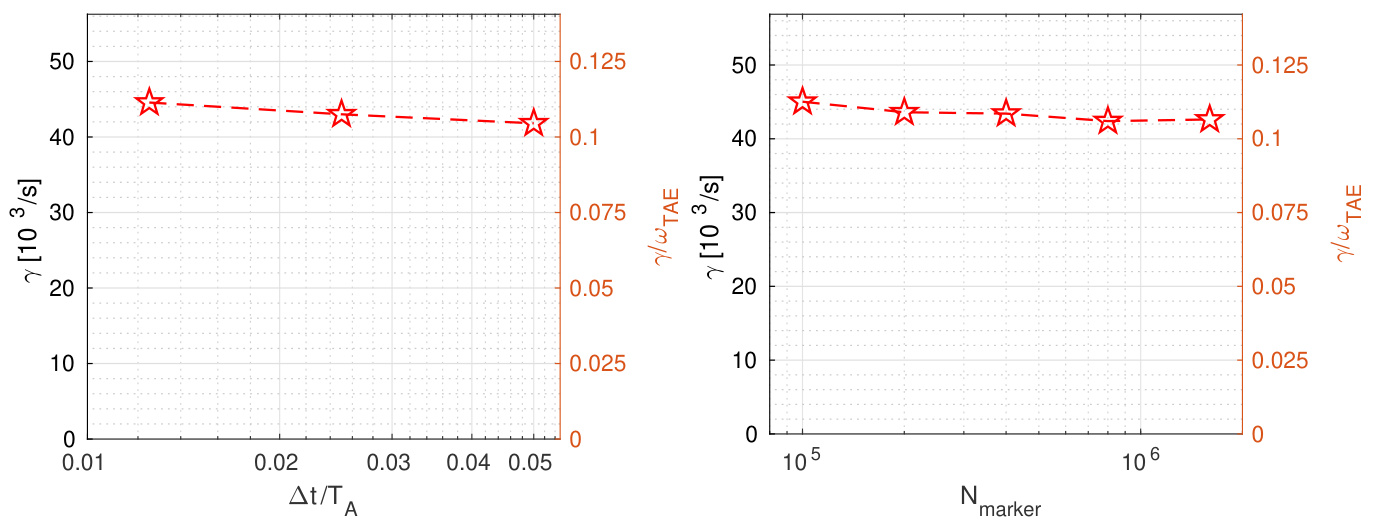
图 2. 不同时间步长（左）和标记粒子数（右）对应的增长率。

即 $T_{\mathrm{A}}=4\pi q(r=r_{\mathrm{c}})R_0/v_{\mathrm{A}}$，其中 $q(r=r_{\mathrm{c}})=q_{\mathrm{c}}=1.75$。对于与标记粒子数相关的收敛性测试，我们选取 $\Delta t/T_{\mathrm{A}}=0.05$，结果如图 2 右图所示。当 $N_{\mathrm{marker}}>2\times 10^5$ 时，可获得良好的收敛性。

式 (38) 中的迭代安培求解器对 $\delta A^{\mathrm{h}}$ 的精确计算以及缓解“抵消”问题至关重要。典型非线性模拟中迭代安培求解器的收敛性如图 3 所示。对于基准情形（$T_{\mathrm{EP}}=400\mathrm{keV}$），可观察到良好的收敛性。EP 驱动的 TAE 被激发，并在 $t/T_{\mathrm{A}}\approx 10$ 后达到饱和。随着迭代次数增加，$\delta A^{\mathrm{h}}$ 的修正量逐渐减小。初始时刻的收敛性优于后期，这是因为在有限轨道宽度效应和镜像力作用下，标记粒子分布偏离麦克斯韦分布，导致 $\delta A_0^{\mathrm{h}}$ 与严格解 ${\sum }_{p=0,1,2\dots }\delta A_p^{\mathrm{h}}$ 之间的偏差更大。尽管如此，在整个模拟过程中收敛性良好，且仅需 4 次迭代即可将 $\delta A^{\mathrm{h}}$ 的修正抑制到低于 $1\%$。

B. EP 驱动 TAE 的线性 $\delta f$ 模拟

在先前工作中，为与其他代码进行基准对比，对不同 EP 温度下的 EP 驱动 TAE 进行了模拟。${}^8$ 为使 TRIMEG-GKK 中的模型尽可能与其他代码一致，对热离子、高能粒子和电子均采用 $\delta f$ 方案。由于我们关注线性解，因此求解线性回旋动理方程时，标记粒子沿未扰动轨迹推进，但其权重随时间演化。我们仅与 ORB5 和 GYGLES 的结果进行比较，因为它们的模型与我们的更为相似。EP 驱动 TAE 的增长率如图 4 所示。在忽略有限拉莫尔半径效应的模型下，结果吻合良好。

$T_{\mathrm{EP}}=400$ keV 时极向谐波的径向模结构如图 5 所示。其模宽度与 ORB5/GYGLES 的结果相当。${}^8$ $m=10$ 谐波的幅值显著高于 $m=11$ 谐波，这也与先前工作中 GYGLES/ORB5 的结果一致。${}^8$

C. 非线性 $\delta f$ 与全 $f$ EP 模拟

非线性模拟分别采用 $\delta f$ 方案和混合全 $f$-EPs-$\delta f$-电子/热离子方案进行。需要注意的是，在混合全 $f$-$\delta f$ 方案中，全 $f$ 方案仅应用于高能粒子（EPs），而电子和热离子始终采用 $\delta f$ 方案处理。为估算适当处理TAE所需的最小标记粒子数，注意到 $\delta \bar{n}\sim \delta \bar{\varphi }(k_{\perp }^2{\rho }_{\mathrm{ti}}^2)\sim 10^{-3}\delta \bar{\varphi }$，$\delta \bar{j}\sim \delta {\bar{A}}_{\parallel }(\beta m_{\mathrm{i}}/m_{\mathrm{e}})/{\rho }_{\mathrm{ti}}^2\sim 6.2\times 10^{-4}\delta \bar{A}$，其中 $\delta \bar{n}$ 和 $\delta \bar{j}$ 分别以电子平衡密度和电子热速度归一化。在饱和水平时，$\delta \bar{\varphi }\sim 1$，$\delta {\bar{A}}_{\parallel }\sim 1$。若对所有粒子种类均采用全 $f$ 方案，则密度和电流中的噪声水平必须远低于 $\delta \bar{n}$ 和 $\delta \bar{j}$，这要求每个自由度（单元数与傅里叶模数的乘积）对应的标记粒子数满足：对于密度，$N_{\mathrm{mark},\mathrm{DOF}}\gg 10^6$；对于电流，$N_{\mathrm{mark},\mathrm{DOF}}\gg 2.6\times 10^6$。

为了减少标记粒子数，同时保留对高能粒子使用全 $f$ 方案的能力，本文对电子和热离子采用 $\delta f$ 方案。因此，主要噪声来源于全 $f$ 高能粒子。由于高能粒子密度小于电子密度的1%，对标记粒子数的要求得以放宽：对于密度，每个单元或每个傅里叶模对应的标记粒子数需满足 $N_{\mathrm{mark},\mathrm{DOF}}\gg 10^2$；对于电流，则需满足 $N_{\mathrm{mark},\mathrm{DOF}}\gg 2.6\times 10^2\sqrt{T_{\mathrm{EP}}{m}_{\mathrm{e}}/(T_{\mathrm{e}}{m}_{\mathrm{EP}})}\sim 0.86\times 10^2$。

图6展示了场能量的时间演化。在全 $f$ 模拟中，通过设置标记粒子数 $N_{\mathrm{e}}=2.5\times 10^5$、$N_{\mathrm{i}}=2.5\times 10^5$、$N_{\mathrm{EP}}=16\times 10^6$ 来控制噪声水平。而在 $\delta f$ 模拟中，$N_{\mathrm{e}}=2.5\times 10^5$、$N_{\mathrm{i}}=2.5\times 10^5$、$N_{\mathrm{EP}}=2.5\times 10^5$。主要计算开销来自于与标记粒子相关的操作，即在标记位置插值场量、利用标记计算密度和电流，以及计算标记轨迹。因此，全 $f$ 案例的计算成本约为 $\delta f$ 案例的20倍，这与全 $f$ 案例中标记总数 $16.5\times 10^6$ 和 $\delta f$ 案例中 $0.75\times 10^6$ 的比例一致。可以清晰地观察到线性增长阶段和模态饱和过程。线性阶段的模结构与 $\delta f$ 模拟结果高度一致。据我们所知，这种高能粒子采用全 $f$、热离子和电子采用 $\delta f$ 的混合方案此前尚未见报道。在我们的研究中，该方法已被验证为切实可行，适用于高能粒子相关物理的研究。据估算，若对电子和离子也采用全 $f$ 方案，本方法可将模拟时间缩短至其 $(n_{\mathrm{EP}}/n_{\mathrm{e}}{)}^2\sim 10^{-4}$。

全 $f$ 模拟的线性增长率和饱和水平相对低于 $\delta f$ 模拟，这是由于高能粒子剖面弛豫导致驱动强度减弱所致。需要注意的是，在全 $f$ 和 $\delta f$ 模拟中均采用了相同的粒子补充方案：损失的粒子在极向位置 ${\theta }_{p,\mathrm{refill}}=-{\theta }_{p,\mathrm{loss}}$ 和环向位置 ${\varphi }_{p,\mathrm{refill}}={\varphi }_{p,\mathrm{loss}}-2q(r_{p,\mathrm{loss}}){\theta }_{p,\mathrm{loss}}$ 处重新填充，其中 $r_{p,\mathrm{loss}}$ 表示损失粒子的径向位置。高能粒子剖面的弛豫源于标记加载过程。局域麦克斯韦分布并非托卡马克几何下的稳态解，即分布函数会在几个粒子穿越周期（$\sim 2\pi q{R}_0/v_{\parallel }$）内发生弛豫。在全 $f$ 方案中，为消除人为效应，应严格采用基于运动不变量空间的高能粒子分布。

这一要素对于不同代码间的基准测试以及实验观测的解释至关重要。

D. 采用正则麦克斯韦分布的全 $f$ 模拟

尽管采用局域麦克斯韦分布的全 $f$ 模拟是一个定义明确的问题，可作为全 $f$ 研究的基准案例，但更重要的是采用基于运动不变量的动理学平衡分布（即正则麦克斯韦分布），并明确正则麦克斯韦分布与局域分布模拟结果之间的差异。图7展示了采用局域麦克斯韦分布和正则麦克斯韦分布时高能粒子剖面的弛豫情况。对于局域麦克斯韦分布（左图），在 $1\sim 2$ 个高能粒子穿越周期内，对数高能粒子梯度减小了约40%；而对于正则分布（右图），梯度几乎保持不变（基准案例中 $T_{\mathrm{EP}}=400$ keV 时，$T_{\mathrm{trans},\mathrm{EP}}/T_{\mathrm{A}}\sim 1$）。然而，正则分布需进行调整以匹配解析径向分布，因为采用平移后的正则环向动量 ${\psi }_{\mathrm{can}}$ 描述的高能粒子分布函数实际上对应于高能粒子轨道中心的分布。

虽然高能粒子导心分布由式(80)给出，但理论上可通过导心与轨道中心之间的前推（push-forward）和拉回（pull-back）变换实现两者转换。在本工作中，该匹配过程可通过数值方法完成。我们运行并调整了若干具有不同参数 $c_0,c_1,c_2,c_3$ 的正则高能粒子分布案例，使得导心密度剖面与式(80)一致。当选择正则高能粒子分布（式46）中的系数为 $(c_0,c_1,c_2,c_3{)}_{\text{can}}=(0.46623,0.17042,0.11357,0.521298)$ 时，可获得良好匹配：

$$n\left({\psi }_{\mathrm{can}}\right)=n\left(r_{\mathrm{can}}\right)=n_{\mathrm{EP},0}{c}_{3,\mathrm{can}}\exp \left(-\frac{c_{2,\mathrm{can}}}{c_{1,\mathrm{can}}}\tanh \frac{r-c_{0,\mathrm{can}}}{c_{2,\mathrm{can}}}\right).$$

对于全 $f$ 案例，标记粒子数设为 $N_{\mathrm{e}}=2.5\times 10^5$、$N_{\mathrm{i}}=2.5\times 10^5$、$N_{\mathrm{EP}}=64\times 10^6$。该匹配案例的导心剖面如图8左图所示，与式(80)描述的ITPA-TAE基准剖面非常接近。原则上，通过在运动不变量空间中采用有限元方法表示高能粒子剖面可实现更精确的匹配，但这超出了本文范围。此外，该方法避免了人为弛豫效应。右图展示了全 $f$ 方案的时间演化，

全 $f$ 与 $\delta f$ 陀螺动理学粒子模拟

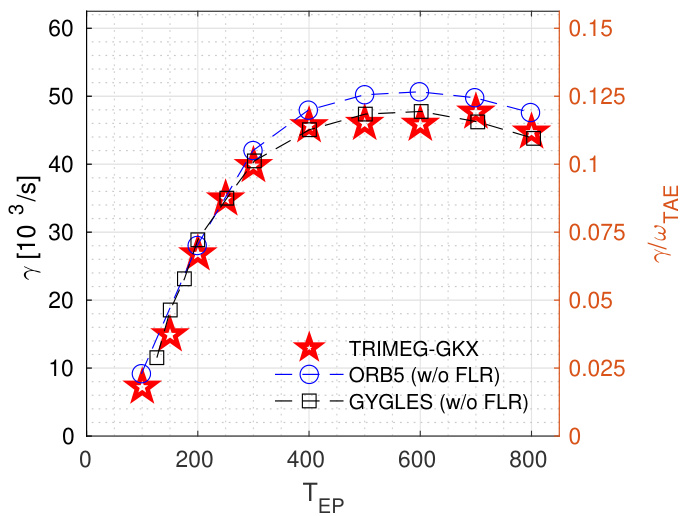
图4. 不同高能粒子温度下，忽略有限拉莫尔半径（FLR）效应模型所得到的高能粒子驱动TAE的增长率。

与 $\delta f$ 方案结果一致。仍可观察到增长率的差异，但仅为约8%，这是由于全 $f$ 与 $\delta f$ 中分布函数的细节结构及其相关的波粒相互作用可能存在差异。尽管如此，采用正则高能粒子分布被证明是一种切实可行的方法，既能避免显著的高能粒子剖面弛豫，又能在全 $f$ 模拟中匹配高能粒子密度剖面。对于本ITPA-TAE案例，高能粒子密度扰动较小（$\delta n/n_0<1\%$），$\delta f$ 方案仍然适用，因此适合比较全 $f$ 与 $\delta f$ 方案。对于更长时间尺度的模拟以及间歇性和瞬态等离子体，高能粒子剖面可能发生更显著的变化，此时全 $f$ 高能粒子方案因其能够描述相空间中任意分布及其时间演化而具有天然优势，而 $\delta f$ 方案则因 $\delta f/f_0$ 增大导致噪声水平升高而效力下降。未来工作将开展更多高能粒子分布具有显著时间演化的模拟研究。

V. 结论

本文在同一框架下构建并实现了全 $f$ 与 $\delta f$ 陀螺动理学粒子模型，并将其应用于高能粒子驱动的环向阿尔芬本征模（TAE）模拟。我们提出了混合全 $f$-$\delta f$ 方案用于阿尔芬波及高能粒子物理研究。该方案在公式推导中采用了混合变量，并在TRIMEMG-GKX中实现了拉回（pullback）算法。

完整的 $f$ 与 $\delta f$ 陀螺动理学（GK）粒子模拟

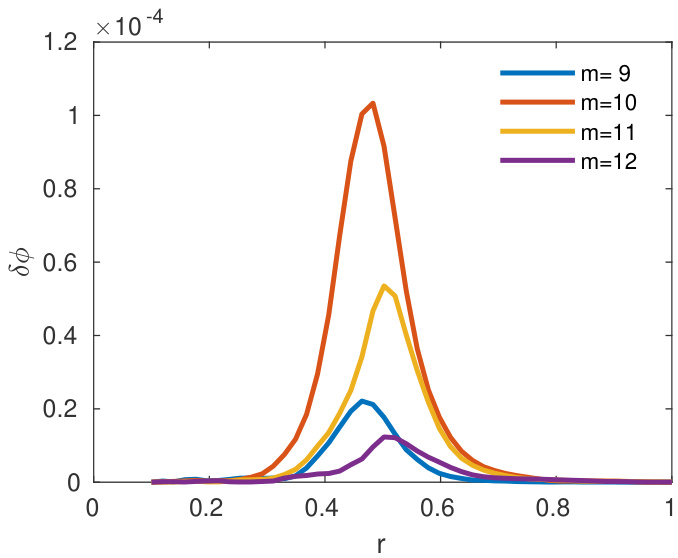
图5. 由高能粒子（EP）驱动的TAE模的极向谐波径向结构，其中高能粒子温度为 $T_{\mathrm{EP}}=400$ keV。图中绘制了四个主导谐波（$m=9,10,11,12$）。

代码在电磁问题模拟方面表现出色，即使对于电子趋肤深度较小的ITPA-TAE情形，也有效缓解了抵消问题。在线性增长速率和模结构方面，本工作结果与其他代码先前的结果吻合良好。

完整的 $f$（EP）模拟揭示了高能粒子的重要物理特性。由于高能粒子能量很高，其有限轨道宽度较大，局域麦克斯韦分布无法很好地近似稳态高能粒子分布。若在完整 $f$ 模拟中采用麦克斯韦高能粒子分布，则在几个穿越周期内，高能粒子分布就会明显偏离初始分布，表现为高能粒子密度梯度减弱的分布弛豫现象。因此，在使用ITPA-TAE参数、$T_{\mathrm{EP}}=400$ keV 的情况下，完整 $f$ 高能粒子模拟得到的线性增长率比 $\delta f$ 模拟低约40%，这表明在完整 $f$ 方案中必须妥善处理高能粒子分布的弛豫效应。本文采用平移后的正则环向动量、粒子能量以及磁矩作为高能粒子的运动不变量，并在此坐标系下定义高能粒子分布，从而更严格地描述高能粒子的稳态分布，避免了人为引起的密度弛豫。此外，本文还引入了一种匹配方案，用于展示从平移后的正则环向动量坐标到高能粒子导心坐标的拉回变换（pullback transform），揭示了有限轨道宽度效应对高能粒子特性的本质影响。本文发展的混合完整-$f$-$\delta f$ 方案

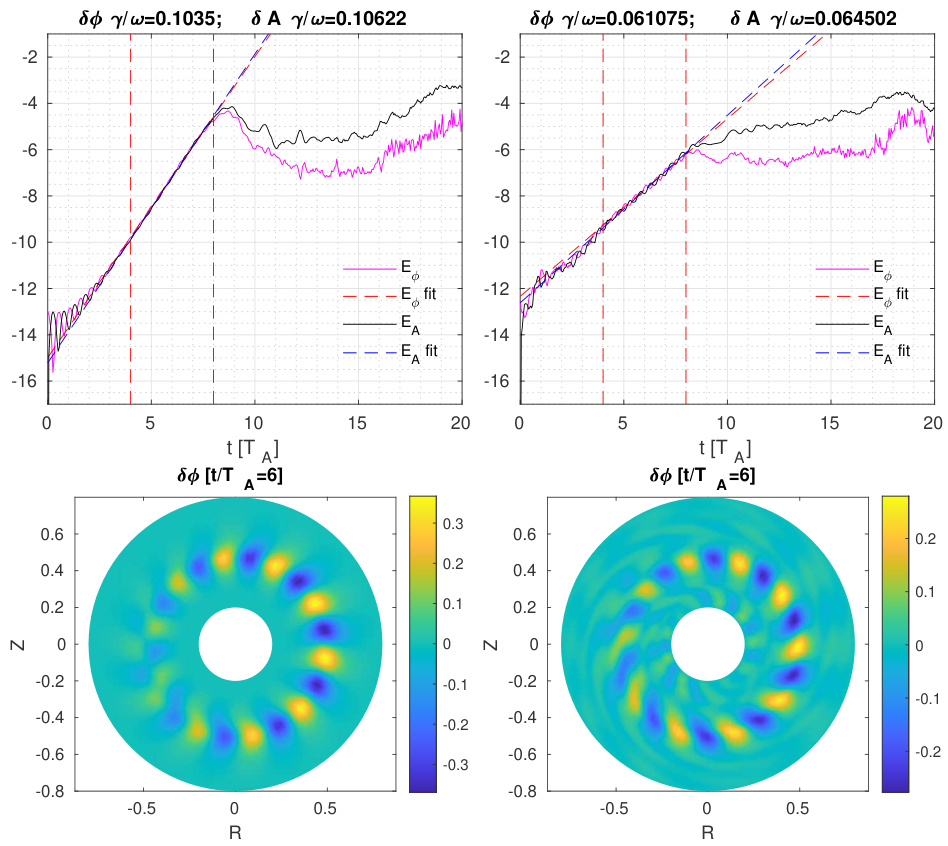
图6. $\delta f$（左上）与完整 $f$（右上）模拟的时间演化。底部展示了线性阶段末期对应的二维模结构。

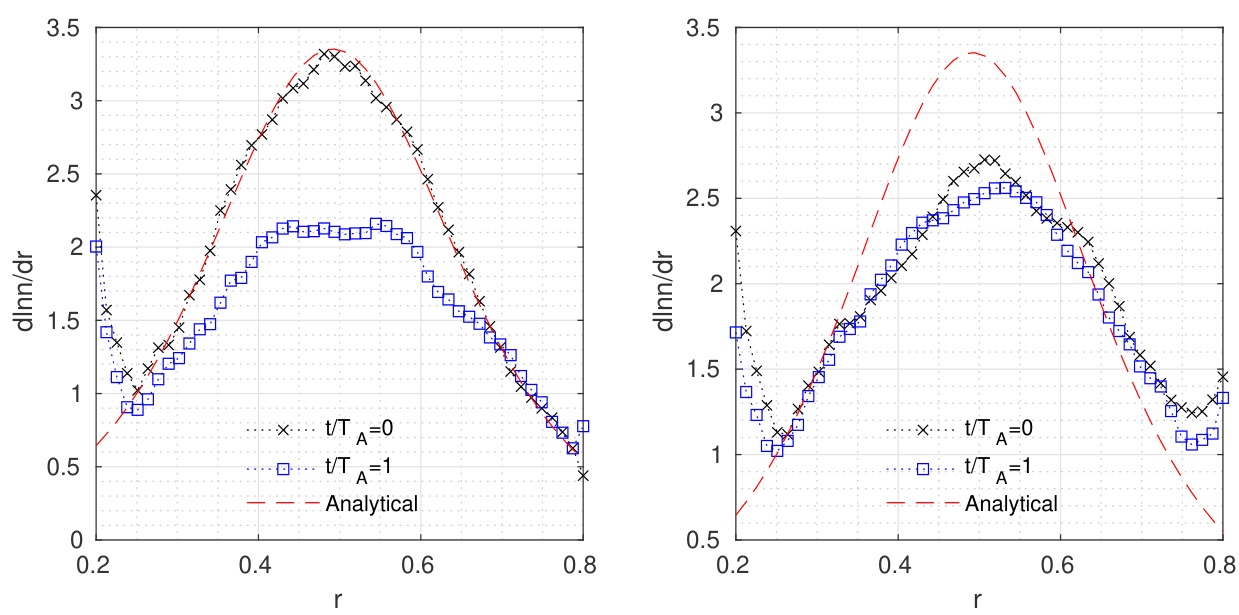
图7. 局域麦克斯韦分布（左）与正则麦克斯韦分布（右）下，标记粒子分布从 $t/T_{\mathrm{A}}=0$ 到 $t/T_{\mathrm{A}}=1$ 的变化情况。局域麦克斯韦分布下标记粒子明显弛豫，而正则麦克斯韦分布下几乎无弛豫。两种情形下均有 $(c_0,c_1,c_2,c_3)=(0.49123,0.298228,0.198739,0.521298)$。

完整 $f$ 与 $\delta f$ 陀螺动理学（GK）粒子模拟

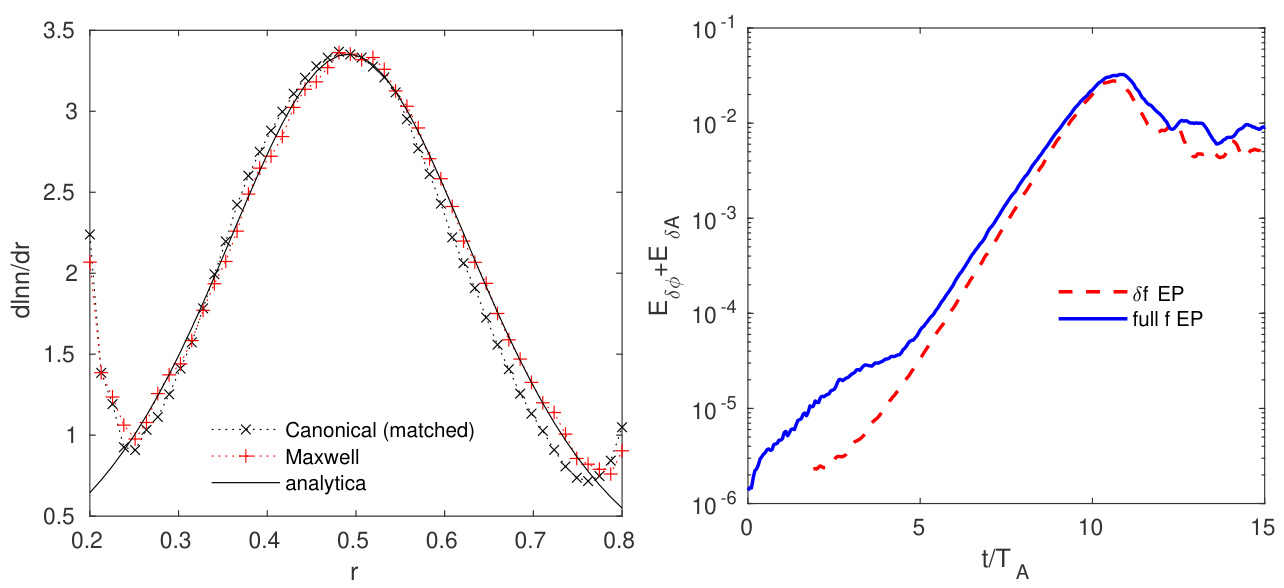
图8. 左图：匹配后的正则麦克斯韦分布，参数为 $(c_0,c_1,c_2,c_3)=(0.46623,0.17042,0.11357,0.521298)$（黑色叉号）；局域麦克斯韦分布，参数为 $(c_0,c_1,c_2,c_3)=(0.49123,0.298228,0.198739,0.521298)$，分别由标记粒子（红色加号）和解析结果（黑色实线）给出。右图：使用局域麦克斯韦高能粒子分布的 $\delta f$ 模拟（红色虚线）与使用正则麦克斯韦高能粒子分布的完整 $f$ 模拟（蓝色实线）所得总场能的时间演化。

使得背景电子和热离子的动力学模拟在计算上更为经济，同时对高能粒子提供了灵活的描述方式，允许高能粒子剖面及其速度空间分布在较大范围内变化。该方法为利用真实实验高能粒子分布开展与间歇性和瞬态等离子体活动相关的动力学研究提供了强有力的工具。

致谢

Z.X. Lu 感谢 A. Mishchenko、F. Zonca、M. Rampp 和 J. Chen 的有益讨论，以及 JOREK 小组、ORB5 小组和 EUTERPE 小组提供的建议。本工作的模拟在 MPCDF 上完成。本研究是在 EUROfusion 联盟框架下开展的，由欧洲联盟通过 Euratom 研究与培训计划资助（资助协议编号 101052200 — EU-ROfusion）。文中表达的观点和意见仅代表作者，并不一定反映欧洲联盟或欧洲委员会的观点。欧洲联盟及欧洲委员会对此不承担任何责任。

附录 A：临时平衡

对于托卡马克几何结构，采用坐标 $(r,\varphi ,\theta )$，磁场表示为 $\mathbf{B}=\nabla \psi \times \nabla \varphi +F\nabla \varphi$，其中 $\mathbf{b}=\mathbf{B}/B$ 为沿磁力线方向的单位矢量。本文采用了一种特设（ad-hoc）平衡位形，其特点是具有同心圆形磁通面且 $F$ 为常数。极向磁通为

$$\psi (r)=\frac{B_0}{2{\bar{q}}_2}\ln \left(1+\frac{{\bar{q}}_2}{{\bar{q}}_0}{r}^2\right),$$

其中 $\bar{q}(r)={\bar{q}}_0+{\bar{q}}_2{r}^2$，${\bar{q}}_2={\bar{q}}_{\mathrm{edge}}-{\bar{q}}_0$。安全因子函数为

$$q(r)=\frac{\bar{q}}{\sqrt{1-(r/R_0{)}^2}}.$$

磁场方向的旋度为

$$(\nabla \times \mathbf{b})\cdot \hat{\mathbf{r}}=\frac{R_0\sin \theta }{R\sqrt{r^2/q^2+R_0^2}}$$

$$(\nabla \times \mathbf{b})\cdot \hat{\theta }=\frac{R_0}{R}\left[\frac{\cos \theta }{\sqrt{r^2/{\bar{q}}^2+R_0^2}}-\frac{Rr({\bar{q}}_0-{\bar{q}}_2{r}^2)}{{\bar{q}}^3(r^2/{\bar{q}}^2+R_0^2{)}^{3/2}}\right]$$

$$(\nabla \times \mathbf{b})\cdot \hat{\varphi }=-\frac{r^2+2R_0^2{\bar{q}}_0\bar{q}}{{\bar{q}}^3(r^2/{\bar{q}}^2+R_0^2{)}^{3/2}}$$

附录 B：特设平衡位形下的导心运动方程

运动的平衡部分如下：

$$\frac{\mathrm{d}{r}_0}{\mathrm{d}t}=b_r^{\ast }{v}_{\Vert }+C_{\mathrm{d}}\frac{F}{r}{\partial }_{\theta }B,$$

$$\frac{\mathrm{d}{\theta }_0}{\mathrm{d}t}=\frac{b_{\theta }^{\ast }}{r}{v}_{\Vert }-C_{\mathrm{d}}\frac{F}{r}{\partial }_{r}B,$$

$$\frac{\mathrm{d}{\varphi }_0}{\mathrm{d}t}=\frac{b_{\varphi }^{\ast }}{R}{v}_{\parallel }+C_{\mathrm{d}}\frac{{\partial }_r\psi }{R}{\partial }_{r}B,$$

$$C_{\mathrm{d}}={\rho }_{\mathrm{N}}\frac{B_{\mathrm{axis}}}{R{B}^2{B}^{\ast }}\frac{M_s}{{\bar{c}}_s}\mu B,$$

$$\frac{\mathrm{d}{v}_{\parallel ,0}}{\mathrm{d}t}=-\frac{\mu b_{\theta }^{\ast }}{r}{\partial }_{\theta }B$$

运动方程的扰动部分为：

$$\frac{\mathrm{d}\delta r}{\mathrm{d}t}=C_{\mathrm{E}}(b_{\varphi }{\partial }_{\theta }\delta G-b_{\theta }{\partial }_{\varphi }\delta G),$$

$$\frac{\mathrm{d}\delta \theta }{\mathrm{d}t}=-\frac{C_{\mathrm{E}}}{r}{b}_{\varphi }{\partial }_r\delta G,$$

$$\frac{\mathrm{d}\delta \varphi }{\mathrm{d}t}=\frac{C_{\mathrm{E}}}{R}{b}_{\theta }{\partial }_r\delta G,$$

$$\delta G=\delta \varphi -v_{\Vert }\delta A_{\Vert }$$

$$\frac{\mathrm{d}\delta v_{\parallel }}{\mathrm{d}t}=C_{\parallel 1}\left(\frac{b_r^{\ast }}{r}{v}_{\parallel }{\partial }_r\delta A^{\mathrm{h}}+\frac{b_{\theta }^{\ast }}{r}{v}_{\parallel }{\partial }_{\theta }\delta A^{\mathrm{h}}+\frac{b_{\theta }^{\ast }}{R}{v}_{\parallel }{\partial }_{\varphi }\delta A^{\mathrm{h}}\right)$$

$$+C_{\parallel 2}\left(\frac{b_{\varphi }}{r}{\partial }_{\theta }B{\partial }_r\delta A^{\mathrm{s}}-\frac{b_{\varphi }}{r}{\partial }_{r}B{\partial }_{\theta }\delta A^{\mathrm{s}}+\frac{b_{\theta }}{R}{\partial }_{r}B{\partial }_{\varphi }\delta A^{\mathrm{s}}\right)$$

$$C_{\mathrm{E}}={\rho }_{\mathrm{N}}\frac{B_{\mathrm{axis}}}{B^{\ast }},C_{\parallel 1}=\frac{{\bar{e}}_s}{M_s},C_{\parallel 2}=-{\rho }_{\mathrm{N}}\mu \frac{B_{\mathrm{axis}}}{B^{\ast }}.$$

参考文献

${}^1$ Lee W 1983 Phys. Fluids 26 556

${}^2$ Chen Y and Parker S E 2007 Journal of Computational Physics 220 839–855

${}^3$ Hatzky R, Kleiber R, Königies A, Mishchenko A, Borchardt M, Bottino A and Sonnendrücker E 2019 Journal of Plasma Physics 85

${}^4$ Mishchenko A, Königies A and Hatzky R 2005 Joint Varenna-Lausanne International Workshop on Theory of Fusion Plasmas (Societa Italiana di Fisica) pp 315–322

${}^5$ Lu Z, Meng G, Hoelzl M and Lauber P 2021 Journal of Computational Physics 440 110384

${}^6$ Sturdevant B J, Ku S, Chacón L, Chen Y, Hatch D, Cole M, Sharma A, Adams M, Chang C, Parker S 等. 2021 Physics of Plasmas 28 072505

${}^7$ Mishchenko A, Bottino A, Biancalani A, Hatzky R, Hayward-Schneider T, Ohana N, Lanti E, Brunner S, Villard L, Borchardt M 等. 2019 Computer Physics Communications 238 194–202

${}^8$ Kölnies A, Briguglio S, Gorelenkov N, Fehér T, Isaev M, Lauber P, Mishchenko A, Spong D, Todo Y, Cooper W 等. 2018 Nucl. Fusion 58 126027

${}^9$ Heikkinen J A, Janhunen S J, Kiviniemi T P 和 Ogando F. 2008 J. Comput. Phys. 227 5582

${}^{10}$ Chang C, Ku S, Tynan G, Hager R, Churchill R, Cziegler I, Greenwald M, Hubbard A 和 Hughes J. 2017 Phys. Rev. Lett. 118 175001

全 $f$ 和 $\delta f$ 吉尔曼-克鲁斯卡（GK）粒子模拟

${}^{11}$ Lu Z, Lauber P, Hayward-Schneider T, Bottino A 和 Hoelzl M. 2019 Phys. Plasmas 26 122503

${}^{12}$ Lanti E, Ohana N, Tronko N, Hayward-Schneider T, Bottino A, McMillan B, Mishchenko A, Scheinberg A, Biancalani A, Angelino P 等. 2020 Computer Physics Communications 251

${}^{13}$ Bottino A, Vernay T, Scott B, Brunner S, Hatzky R, Jolliet S, McMillan B, Tran T M 和 Villard L. 2011 Plasma Physics and Controlled Fusion 53 124027

${}^{14}$ Hager R, Ku S H, Sharma A, Chang C 和 Churchill R. 2022 arXiv 预印本 arXiv:2202.06124

${}^{15}$ Angelino P, Bottino A, Hatzky R, Jolliet S, Sauter O, Tran T 和 Villard L. 2006 Phys. Plasmas 13 052304