双电流片等离子体中撕裂模的爆发相：平衡磁场位形对起爆阈值和增长率的影响

HUBERT BATY${}^1$

${}^1$ 斯特拉斯堡天文台，斯特拉斯堡大学
11 Rue de l'université, 67000 斯特拉斯堡，法国
hubert.baty@unistra.fr

摘要

本文在二维笛卡尔坐标系下，采用约化电阻磁流体力学（MHD）框架，研究了双电流片系统中撕裂不稳定性所引发的磁重联现象。特别利用自适应有限元代码 FINMHD 对其非线性爆发相进行了深入探索。我们获得了临界纵横比，即在经历线性阶段和早期非线性饱和阶段之后，系统发生非线性失稳所需的最小 $L/x_s$ 比值（其中 $L$ 为系统的周期长度，$x_s$ 为两个电流层之间距离的一半）。该阈值与所选初始平衡态（类双 Harris 磁场分布）的具体细节及电阻率无关，其值为 4.7，接近且略小于以往研究中采用更特殊平衡位形所得出的约 5 的数值。动能（$E_K$）的时间演化遵循双重指数规律，即 $E_K\propto \exp \left[e^{({\gamma }^{\ast }t)}\right]$，其中伪增长率 ${\gamma }^{\ast }\simeq 0.1t_A^{-1}$（$t_A$ 为特征阿尔芬时间），同样与位形和电阻率无关。该机制为天体物理等离子体（如日冕）中已存在双电流片结构时，在快速阿尔芬时间尺度上突然发生的爆发性磁能释放现象提供了一种可能的解释。

关键词：磁重联 – 磁流体力学（MHD）– 等离子体 – 太阳：耀斑

1. 引言

电流片等离子体中发展的撕裂模被认为在多种磁化天体物理系统（如日冕、太阳风或脉冲星风）中观测到的爆发性现象中起着重要作用。当存在单一电流片（对应磁场反转）时，撕裂不稳定性通常被视为一种慢模，因为它涉及磁重联过程，表现为磁岛在电阻时间尺度上增长（除非在非常长而薄的电流层中能够形成等离子体团链）。本文所研究的此类高导电等离子体中的撕裂模已在平面和片状箍缩构型中被广泛研究（Priest & Forbes 2000）。该磁流体力学（MHD）不稳定性具有波数 $k$ 的阈值特性，要求 $k\le k_M$。最大波数 $k_M$ 依赖于平衡剖面的具体形式，对于标准 Harris 剖面，其值为 $k_M=1/a$，其中 $a$ 定义为电流片的半厚度。该线性稳定性阈值可直接转换为系统长度的条件 $L\ge L_{min}$，其中 $L_{min}=2\pi /k_M$（Biskamp 2009）。这些电阻不稳定性通常以 $S^{1/3}-S^{3/5}$ 的特征时间增长，其中 Lundquist 数 $S$ 定义为 $S=a{V}_A/\eta$（$V_A$ 和 $\eta$ 分别为阿尔芬速度和小磁扩散系数）。例如，日冕等离子体的典型 $S$ 值约为 $10^{10}$，其对应的撕裂特征时间尺度比太阳耀斑中观测到的快速时间尺度（几分钟）慢多个数量级（即几年/几个月 vs. 几分钟）。

另一方面，此类等离子体中也可能因多次磁场反转而形成多重电流片，从而引发多重撕裂不稳定性。因此，重联过程及其相关的磁能释放将展现出比单电流片更丰富的动力学行为和多阶段特征。双电流片系统即属此类情形。有趣的是，在这种构型下，可观察到与所谓双撕裂模（以下简称 DTM）相关的爆发性增长相。事实上，在经历长时间尺度的缓慢电阻性线性增长（与单撕裂模具有相似的标度律）及随后的饱和阶段后，DTM 会突然转变为快速增长（Ishii et al. 2002; Wang et al. 2007; Janvier et al. 2011; Zhang & Ma 2011; Akramov & Baty 2017）。在此爆发相中，与流动相关的动能可在几个阿尔芬时间内增长数个数量级，且几乎与电阻率 $\eta$ 或 Lundquist 数 $S$ 无关。大量基于最简 MHD 框架（即二维平面几何中的约化 MHD 方程）的研究表明，该爆发相由结构驱动的非线性不稳定性触发（Ishii et al. 2002; Janvier et al. 2011）。这种理想 MHD 不稳定性的起因被归结为在两个电流层上增长的磁岛发生临界形变。只有当纵横比 $L/x_s$（其中 $L$ 为周期系统长度，$x_s$ 为两个电流层之间距离的一半）超过临界值（约为 5）时，才会触发爆发性重联，且该临界值与电阻率无关。否则，包含两个磁岛的系统将不再演化。该第二临界长度值 $L_c$ 通常大于前述的 $L_{min}$。

然而，此前的研究大多采用了一种特定的磁场剖面作为初始不稳定平衡态，这种剖面通常用于实验室等离子体研究。本文的目的正是通过采用另一种剖面（即单电流片撕裂模研究中常用的 Harris 型剖面的推广形式）来检验该临界纵横比值的鲁棒性。此外，我们的剖面参数化方法允许独立于两层间距 $2x_s$ 来研究剪切参数（由磁场反转位置处两个电流层的厚度决定）的影响。最后，我们还研究了先前报道的非线性增长的快速阿尔芬时间尺度如何依赖于初始平衡态以及与非线性阈值的“距离”。我们使用了一个强自适应有限元代码 FINMHD，该代码专为在二维笛卡尔坐标系下、约化电阻 MHD 框架内处理此类重联问题而设计。本文结构如下：第 2 节简要介绍代码和初始设置；第 3 节展示结果；第 4 节给出结论。

2. FINMHD 代码与初始设置

在二维（2D）（即 $x-y$ 平面）中，约化 MHD 方程组通常被认为是描述垂直于主导且恒定磁场分量（$B_z$）平面内动力学的良好近似。在此情况下，2D 平面内的不可压缩性假设被认为是合理的。与采用垂直速度和磁场矢量（分别为 $\mathbf{V}$ 和 $\mathbf{B}$）的标准表述相比，使用标量变量（如流函数，下文记为 $\varphi$ 和 $\psi$）的表述通常更具优势，因为这能确保这两个矢量的无散性。此外，为便于数值实现，FINMHD 采用了一种（无量纲）模型，以电流密度 $J$ 和流涡度 $\omega$ 作为主要变量（Baty 2019）：

$$\begin{array}{r}\frac{\partial \omega }{\partial t}+(\mathbf{V}\cdot \nabla )\omega =(\mathbf{B}\cdot \nabla )J+\nu {\nabla }^2\omega ,\end{array}$$

$$\begin{array}{r}\frac{\partial J}{\partial t}+(\mathbf{V}\cdot \nabla )J=(\mathbf{B}\cdot \nabla )\omega +\eta {\nabla }^2(J-J_e)+g(\varphi ,\psi ),\end{array}$$

$${\nabla }^2\varphi =-\omega ,$$

$${\nabla }^2\psi =-J,$$

其中 $g(\varphi ,\psi )=2\left[\frac{{\partial }^2\varphi }{\partial x\partial y}\left(\frac{{\partial }^2\psi }{\partial x^2}-\frac{{\partial }^2\psi }{\partial y^2}\right)-\frac{{\partial }^2\psi }{\partial x\partial y}\left(\frac{{\partial }^2\varphi }{\partial x^2}-\frac{{\partial }^2\varphi }{\partial y^2}\right)\right]$。我们引入了两个流函数 $\varphi (x,y)$ 和 $\psi (x,y)$，定义为 $\mathbf{V}=\nabla \varphi \wedge {\mathbf{e}}_z$ 和 $\mathbf{B}=\nabla \psi \wedge {\mathbf{e}}_z$（${\mathbf{e}}_z$ 为垂直于 $xOy$ 模拟平面的单位矢量）。注意，$J$ 和 $\omega$ 分别是电流密度和涡度矢量的 $z$ 分量，即 $\mathbf{J}=\nabla \wedge \mathbf{B}$ 和 $\omega =\nabla \wedge \mathbf{V}$（单位制中取 ${\mu }_0=1$）。此外，我们通过 $\eta {\nabla }^{2}J$ 项考虑电阻扩散（为简化起见，假设电阻率 $\eta$ 均匀），并以类似方式引入粘性项 $\nu {\nabla }^2\omega$（$\nu$ 为粘性参数）。上述定义源于选择 $\psi \equiv A_z$，其中 $A_z$ 是矢势 $\mathbf{A}$ 的 $z$ 分量（因 $\mathbf{B}=\nabla \wedge \mathbf{A}$）。FINMHD 代码基于有限元方法，使用非结构化网格上的三角形单元和二次基函数。为稳定离散前两个方程中出现的拉格朗日导数，采用了特征 Galerkin 格式。此外，开发了一种高度自适应（空间和时间上）的方案，以追踪解的快速演化，可选用一阶时间积分器（线性无条件稳定）或二阶积分器（受 CFL 时间步长限制）。通常，可在每个时间步计算一个新的自适应网格，通过寻找使估计误差近似均匀的网格来实现。更具体地说，该方法利用电流密度的 Hessian 矩阵作为主要细化参数，确保在任何时刻都能用几十个三角形单元覆盖电流结构。FINMHD 中使用的技术已在多个挑战性测试中得到验证，包括对流方程的非定常强各向异性解、粘性 Burgers 方程的激波结构形成，以及约化 MHD 方程组的磁重联问题。有关数值格式的更多细节，请参阅 Baty (2019)，以及以下参考文献中关于 MHD 框架下磁重联不同方面的应用（Baty 2020a,b,c）。

通过为磁场剖面的 $y$ 分量 $B_y=B_e(x)$ 选取解析表达式，考虑一个初始一维平衡态。在本工作中，假设采用一种类双 Harris 剖面（下文称为 'tanh'）：

$$B_e(x)=B_0\left[1+\tanh \left(\frac{x-x_s}{a}\right)-\tanh \left(\frac{x+x_s}{a}\right)\right],$$

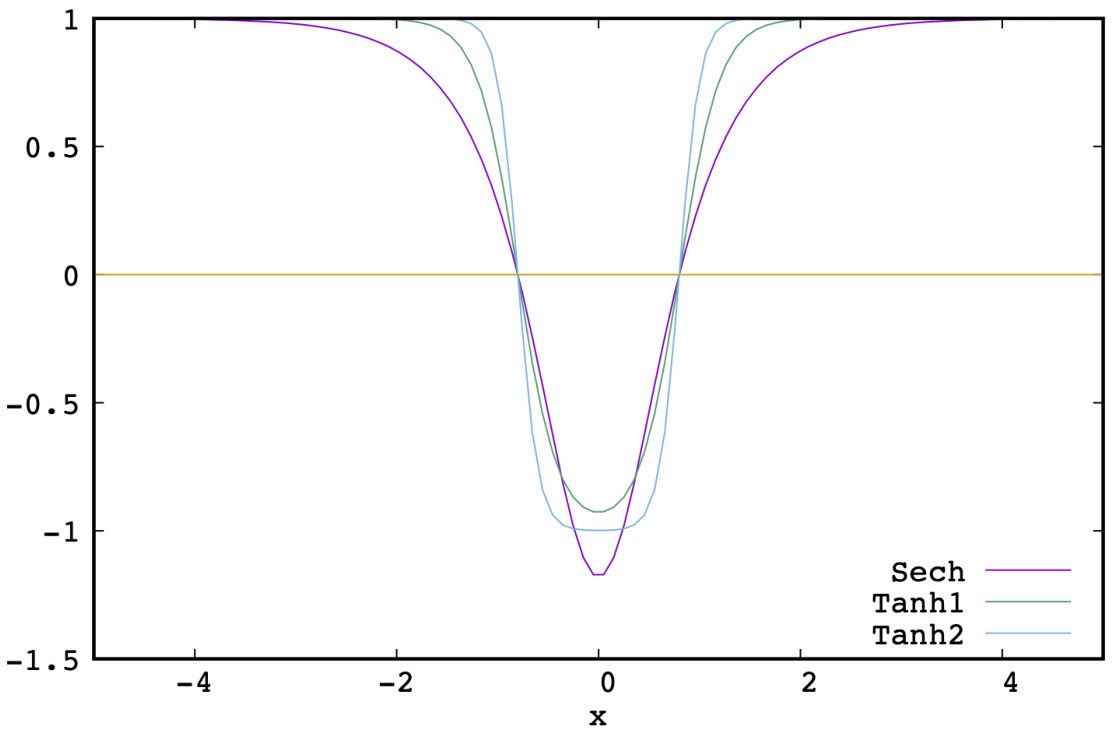
图 1. 'sech' 剖面及两种类 Harris 'tanh' 剖面（'tanh2' 使用 $a=0.2$，'tanh1' 使用 $a=0.4$）的初始平衡磁场 $B_e(x)/B_0$ 配置。不同平衡态的磁场反转点（与水平线交点）位于 $x=\pm x_s=\pm 0.8$。

该剖面在 $x=\pm x_s$ 处具有两个双曲正切型反转，磁剪切由长度尺度 $a$ 定义，远距离处的渐近磁场幅度为 $B_0$。对应的电流密度为：

$$J_e(x)=\frac{B_0}{a}\left[\frac{1}{{\cosh }^2[(x-x_s)/a]}-\frac{1}{{\cosh }^2[(x+x_s)/a]}\right],$$

该表达式也用于方程 (2) 中，以通过 $-\eta {\nabla }^2{J}_e$ 源项防止理想平衡态的扩散。当电阻率参数不够小时，这种扩散是不希望出现的。此外，真正的理想 MHD 平衡态应包含热压力项 $P(x)$ 或垂直磁场分量的 $x$ 依赖性（即模型中未包含的 $B_z(x)$），以确保动量 MHD 方程中满足 $\mathbf{J}\times \mathbf{B}-\nabla P=0$。然而，仅使用涡度方程时，只需 ${\mathbf{B}}_e\cdot \nabla J_e=0$，这自动满足（见方程 1）。

在大多数先前的研究中（例如 Janvier et al. (2011)），采用了另一种平衡磁场位形（下文称为 'sech'）：

$$B_e(x)=B_0\left[1-(1+b_c)\mathrm{sech}(\zeta x)\right],$$

其中参数 $b_c$ 和 $\zeta$ 的选取方式是通过 $\text{sech}(\zeta x_s)=1/(1+b_c)$ 来设定反转位置 $x_s$，此时局部磁剪切等于 $\pi /2$。例如，对于一个平衡态 $x_s=0.8$，使用了 $b_c=1.18$ 和 $\zeta =1.77$，其结果如图 1 所示。还可以将该剖面与我们采用两种不同磁剪切值的“tanh”平衡态进行比较，即电流层半厚度分别为 $a=0.2$ 和 $a=0.4$。

3. 结果

为了全面了解 DTM 演化过程中导致爆发阶段的物理情景，我们下面展示一个具有代表性的不稳定“tanh”平衡剖面的模拟结果，其中 $x_s=0.8$、$a=0.3$。周期性纵向长度取为 $L=4$。在此情况下，首先可以验证 DTM 模式在线性意义上是不稳定的，因为对应的归一化波数 $ka=2\pi a/L\simeq 0.47$ 确实小于 1。等价地，所选长度 $L$ 大于该“tanh”平衡剖面对应的 DTM 线性失稳所需的临界最小长度 $L_{\min }$，即 $L_{\min }\simeq 1.88$。所选电阻率参数为 $\eta =10^{-3}$，磁普朗特数为 $P_r=\nu /\eta =1/3$。在本研究中，我们考虑低粘性情形，以便与先前采用零粘性假设的研究（Janvier 等，2011）进行比较。

还需注意，我们设定 $B_0=1$ 作为归一化基准。因此，时间变量 $t$ 以阿尔芬时间 $t_A=l/V_A$ 进行归一化，其中 $l$ 为单位长度，$V_A$ 为基于 $B_0$ 的阿尔芬速度（即 $V_A=1$）。本工作的模拟区域位于 $x$ 范围 $[-L_x/2:L_x/2]$ 内，其中 $L_x=4$，使得外边界足够远离，不会影响主要动力学过程。在 $x=\pm L_x/2$ 处施加固定边界条件。在 $y$ 方向采用周期性边界条件，以便根据 $k_m=2\pi m/L$（$m$ 为整数）选择不同的波数 $k_m$，其中 $L_y=L$。本工作中线性增长最快的 DTM 不稳定性对应于 $m=1$ 模式，即在每个电流层上形成一个 $m=1$ 的磁岛（见下文）。

对于该代表性案例，由于采用了自适应网格加密策略，模拟过程中三角形单元的最小边长在 $h_{\min }\simeq 0.01$（用于解析早期平衡结构）到 $h_{\min }\simeq 0.001$（用于解析强非线性阶段中强烈的局域次级电流层）之间变化。设定的最大边长为 $h_{\max }\simeq 0.1$，主要用于电流密度极低的区域。对应的三角形单元总数大约在 15000 到 35000 之间。需要注意的是，当采用更小的电阻率时，需要更多的三角形单元和更小的最小边长。

3.1. 爆发性 DTM 动力学概述

图 2（左图）展示了在整个计算域内测得的最大涡度 ${\omega }_M$ 和最大电流密度 $J_M$ 的时间演化，而右图则绘制了相应的最大速度幅值（$V_y$ 分量）和动能 $E_K$ 的时间演化。在早期阶段，经过一段短暂的振荡数值噪声（例如在 $E_K$ 曲线中几乎不可见）后，可以清楚地看到在 $t\lesssim 100$ 时 DTM 的线性发展阶段，此时 ${\omega }_M$、$V_y$ 和 $E_K$ 在半对数坐标下均呈现随时间线性增长的趋势。$E_K$ 的斜率显然是 $V_y$ 或 ${\omega }_M$ 斜率的两倍，代表了线性增长率。更准确地说，DTM 不稳定性的线性增长率 ${\gamma }_l$ 可表示为 ${\gamma }_l={\partial }_t{E}_K/E_K$。需要注意的是，对于此类电阻性不稳定性，${\gamma }_l\propto {\eta }^{3/5}\propto S^{-3/5}$（Biskamp，2009）。图 3 展示了不同时刻电流密度变形及其对应磁场拓扑结构的空间分布。如预期所示，DTM 的特征是在两个初始电流层上分别形成两个磁岛。此外，所观测到的本征模态表现为反对称结构，即两个电流层上的磁岛相位相反：一个电流片上磁岛的 $O$ 点正对着另一个电流片上磁岛的 $X$ 点。线性稳定性分析表明，这种被称为 A 模（Wei 等，2020）的反对称模态将主导另一种对称模态（称为 S 模）。

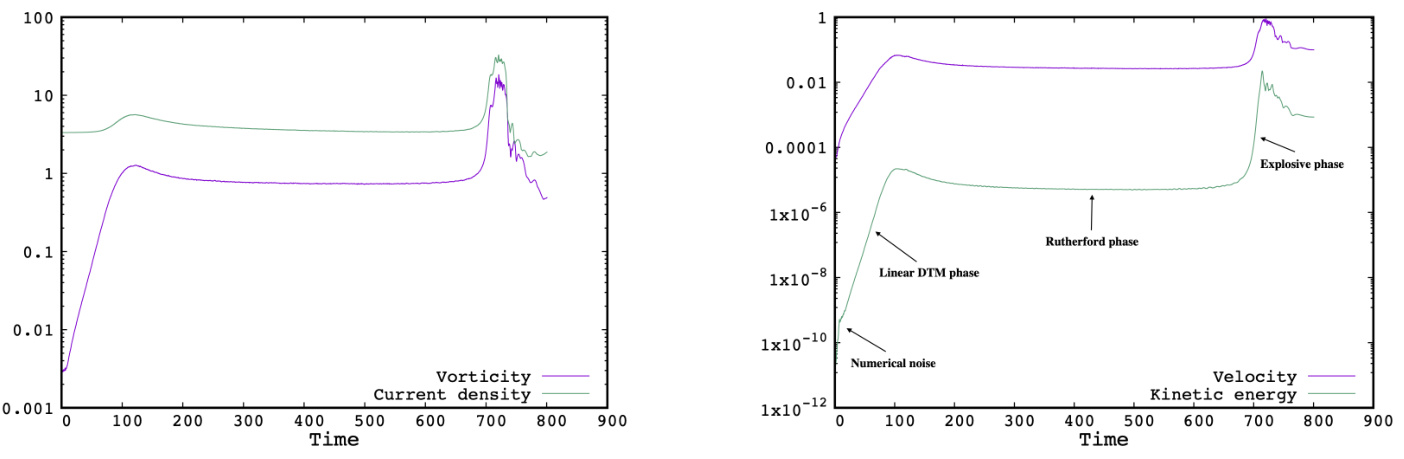
图 2.（左图）最大涡度 ${\omega }_M$ 及对应最大电流密度 $J_M$ 的时间演化，该案例在 $t\simeq 700$ 时表现出爆发性非线性演化；（右图）对应的最大速度（$V_y$ 分量）和动能 $E_k$ 的时间演化。时间以阿尔芬时间单位 $t_A$ 表示（见正文）。

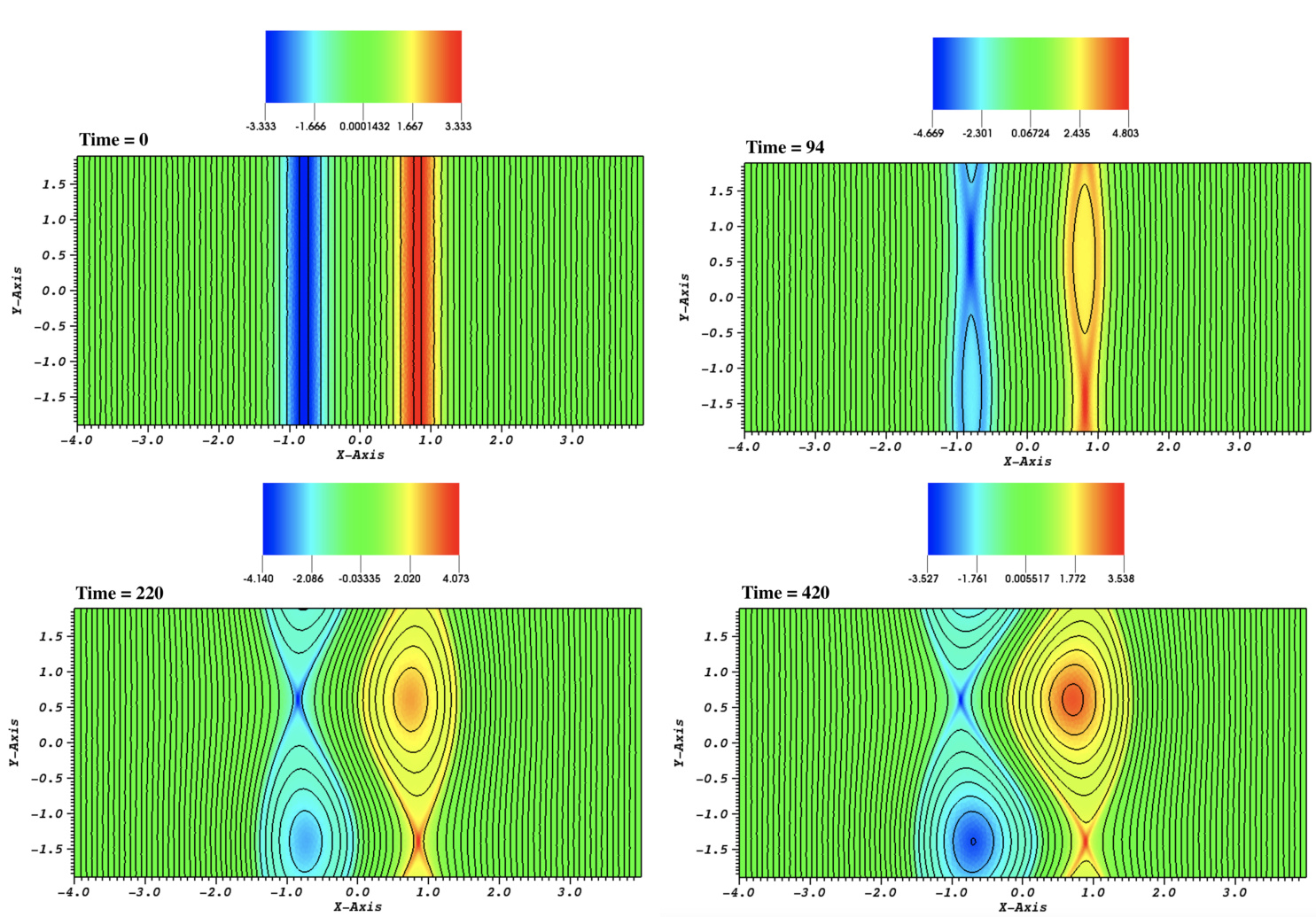
图 3. 在前图所示代表性模拟案例中，不同时刻的电流密度彩色等值线图（见正文），并叠加了相应的磁力线。仅选取对应前两个阶段的早期时刻。

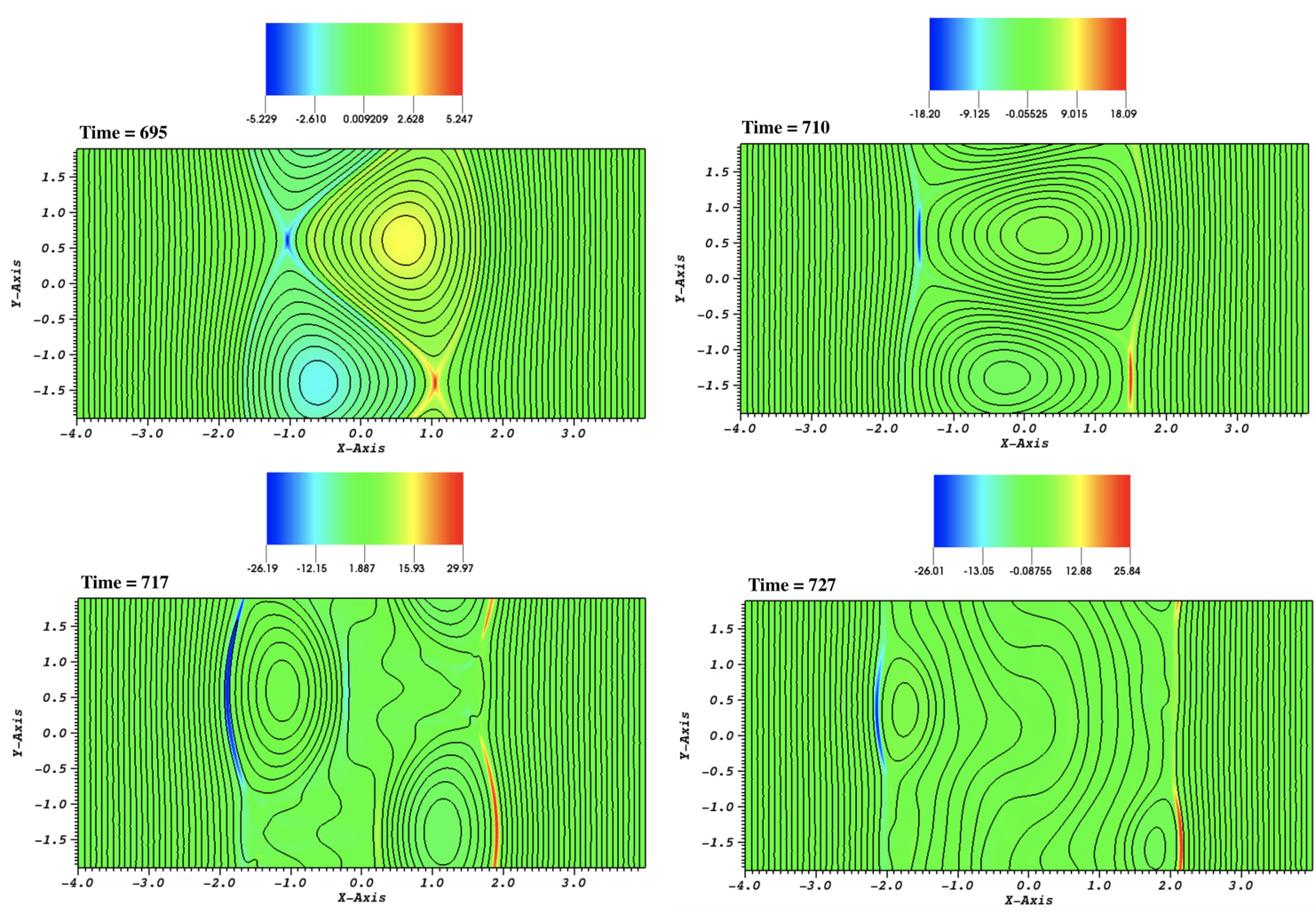
图 4. 与前图相同，但针对 $t\gtrsim 700$ 的后期时刻，聚焦于爆发阶段。

线性阶段之后是被称为 Rutherford 区域的饱和阶段，该阶段已在单撕裂模研究中被广泛探讨。在此阶段，$E_K$ 基本保持稳定，但扰动磁能（未显示）继续以代数形式增长（参见 Janvier 等（2011）及其参考文献），因为流体速度场与磁通量已解耦。该第二阶段演化时间相当长（至少对于本案例所选参数而言），两个磁岛在纯电阻时间尺度上持续增长（见图 3 中 $t=220$ 和 $t=420$ 的快照）。

在 Rutherford 阶段之后，图 2 中在 $t\sim 700$ 时观察到所有物理量的急剧增长。图 4 中叠加了磁力线的电流密度等值线图显示，第三阶段始于磁岛的突然三角形变形（$t=695$ 的快照）。随后，两个 $X$ 点处的电流密度增加（见 $t=710$ 的快照），驱动了第二阶段的磁重联，直至磁岛内部所有闭合磁力线与外部磁力线完全重联（即 $t\simeq 730$）。模拟结束时的最终状态趋向于一种无磁岛和电流层的弛豫构型，对应的磁力线也趋于再次变直。

需要注意的是，后一阶段的磁重联过程与线性 DTM 相关的重联过程相反：在线性增长阶段，闭合磁力线形成，而在爆发阶段则消失。这种爆发性重联动力学的机制被识别为一种结构驱动的不稳定性，其阈值归因于磁岛的临界变形（Janvier 等，2011）。总之，研究表明，只有当比值 $L/x_s$ 大于约 5 时（参见 Janvier 等（2011）中的图 2），非线性失稳才会发生（针对“sech”剖面）。在本工作中，我们采用了一个“tanh”剖面的案例，其比值恰好为临界值，即 $L/x_s=5$。

因此，我们现在研究该临界纵横比值的存在性及其对初始磁平衡的依赖性。

3.2. 关于爆发性重联的临界纵横比

遵循 Janvier 等（2011）所用的方法，我们首先针对固定 $x_s$ 值（即上文参考案例中的 $x_s=0.8$）探索不同的 $L$ 情况。图 5 绘制了以动能演化为主要判据来区分稳定与非线性失稳的结果。可以清楚地看到，本构型的临界 $L_c$ 值估计接近 3.7，因为 $L=3.6$ 的案例未表现出任何突然的非线性增长（而 $L=3.8$ 的案例则有）。实际上，非线性稳定的模拟最终形成饱和磁岛，其结构类似于图 3 中最后一幅图所示。因此，$L/x_s$ 的临界纵横比估计为 $3.75/0.8\simeq 4.7$，该值与 Janvier 等（2011）针对“sech”剖面预期的 5 相比略低但相近。

其次，我们通过在 0.2 到 0.4 之间改变 $a$ 来研究对 $x_s$ 处平衡剪切的依赖性。无论剪切值如何，均恢复相同的临界值 $L_c\simeq 3.75$，如图 6（左图）中 $a=0.2$ 的案例所示。因此，我们可以得出结论：对于我们的“tanh”平衡剖面，临界纵横比与剪切无关。读者需注意，对于 $a=0.2$ 和 $a=0.4$，线性 DTM 不稳定性的最小长度值分别为 $L_{\min }=1.26$ 和 3.1。因此，在两种情况下，$L_{\min }$ 均小于 $L_c$。

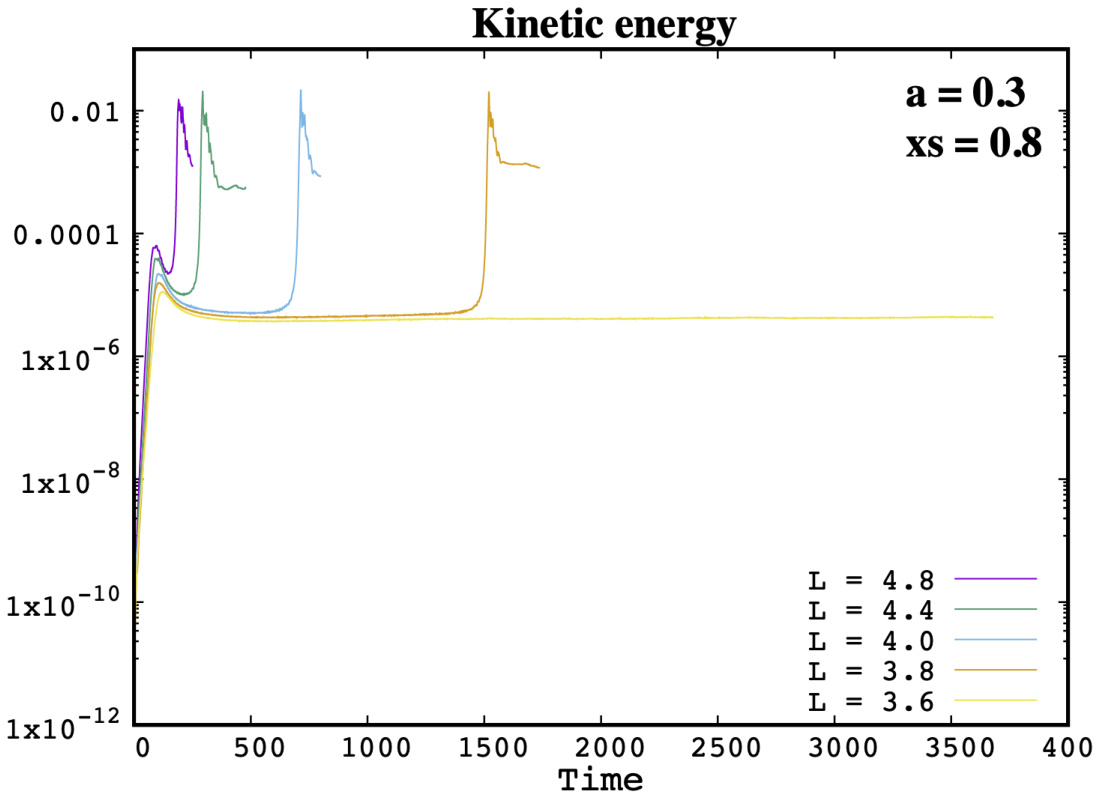
图 5. 采用五种不同长度值 $L=4.8,4.4,4.0,3.8$ 和 3.6 时动能 $E_K$ 的时间演化。初始“tanh”平衡态参数为 $x_s=0.8$、$a=0.3$，其他参数为 $\eta =10^{-3}$ 和 $P_r=1/3$。

最后，我们通过改变 $x_s$ 参数来研究对两个电流片间距的依赖性。图 6 右图展示了 $x_s=0.5$、$a=0.2$ 的模拟结果。此时可推断出更小的临界值 $L_c\simeq 2.35$（介于 2.3 与 2.4 之间），但再次得到相同的临界纵横比 $L_c/x_s=4.7$。

我们得出结论：对于双哈里斯型“tanh”剖面，非线性不稳定性的临界纵横比显然与平衡态的具体细节无关。此外，与 Janvier 等（2011）先前针对“sech”构型得到的约 5 的值相比，该值可能仅略微依赖于整体剖面形状。这可能是由于“sech”剖面中两个电流片外侧区域（即 $x\ge x_s$ 或 $x\le -x_s$）存在额外的磁梯度（见图 1）。事实上，已有研究表明，外部电流的存在会影响

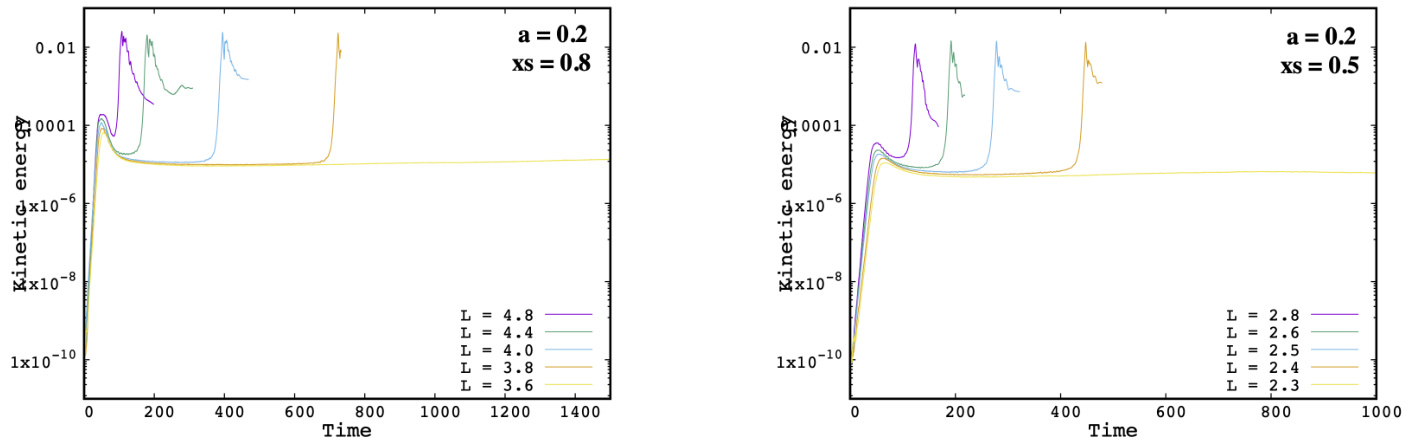
图 6. 采用五种不同长度值（见图例）时动能 $E_K$ 的时间演化。左图和右图分别采用“tanh”平衡态，参数为 $x_s=0.8$、$a=0.2$ 和 $x_s=0.5$、$a=0.2$。

单撕裂模演化中磁岛的增长及其饱和水平（Poyé 等，2013）。然而，我们提醒读者注意，这种差异也可能源于两项研究中不同的数值处理方法。

通过探索采用另一电阻率值（$\eta =3\times 10^{-4}$）的额外案例，我们验证了临界纵横比与电阻率无关，这与先前的结论一致（Janvier 等，2011）。

3.3. 关于爆发性重联的时间尺度

另一个重要问题是爆发增长阶段的特征时间尺度。先前研究表明，该时间尺度对电阻率的依赖性极弱甚至完全无关（Wang 等，2007；Janvier 等，2011；Zhang & Ma，2011；Akramov & Baty，2017）。此外，其增长速度比简单指数增长更快，即扰动物理量（如动能）的增长快于 $\sim \exp ({\gamma }^{\ast }t)$ 的标度律，其中 ${\gamma }^{\ast }$ 表示瞬时增长率。Janvier 等（2011）提出了一种形式为 $\sim \exp \left[t{e}^{({\gamma }^{\ast }t)}\right]$ 的时间依赖关系，而 Akramov & Baty（2017）则提出了另一种形式 $\sim \exp ({\gamma }^{\ast }{t}^2)$。

在本工作中，我们通过爆发增长期间动能的变化考察了时间依赖关系，发现其遵循另一种超指数增长。事实上，我们的结果最佳拟合为双重指数形式 $E_k\sim \exp [e^{({\gamma }^{\ast }(t-t_0))}]$，其中 $t_0$ 可视为接近爆发增长阶段起始时刻的时间点。图 7 展示了本文上述代表性案例的结果。更具体地，我们采用 $t_0=688t_A$ 和 ${\gamma }^{\ast }=0.1t_A^{-1}$，以准确近似 [688 : 710] 时间范围内的爆发阶段。在此之前的时刻，非线性不稳定性尚未触发；在此之后，由于最终弛豫而出现饱和（见图 2）。值得注意的是，该结果在不同“tanh”平衡细节下均成立，且具有相同的伪增长率 ${\gamma }^{\ast }\simeq 0.1t_A^{-1}$。最后，我们还验证了该结果对不同不稳定 $L>L_c$ 值均成立，意味着其也与距非线性阈值的距离 $L-L_c$ 无关。这一点在图 5-6 中不同爆发阶段的比较中已可见。当然，当 $L-L_c$ 过大时，Rutherford 区域将不存在，此时情况显然不同。

需注意，这种双重指数增长在纯二维不可压缩流体动力学中已被证明是可能的，其源于涡度梯度驱动的不稳定构型（Denisov，2015；Kiselev & Sverak，2014）。

4. 结论

本工作证实了在双电流片系统中存在非线性爆发增长的临界纵横比 $L_c/x_s$。该值与磁平衡的具体细节无关，对于本研究中考虑的双哈里斯型“tanh”剖面，其值为 $L/x_s\simeq 4.7$。该阈值与 Janvier 等（2011）基于另一种 MHD 平衡态（即“sech”剖面）得出的值（约 5）相似但略小。这种微小差异可能归因于平衡态的差异

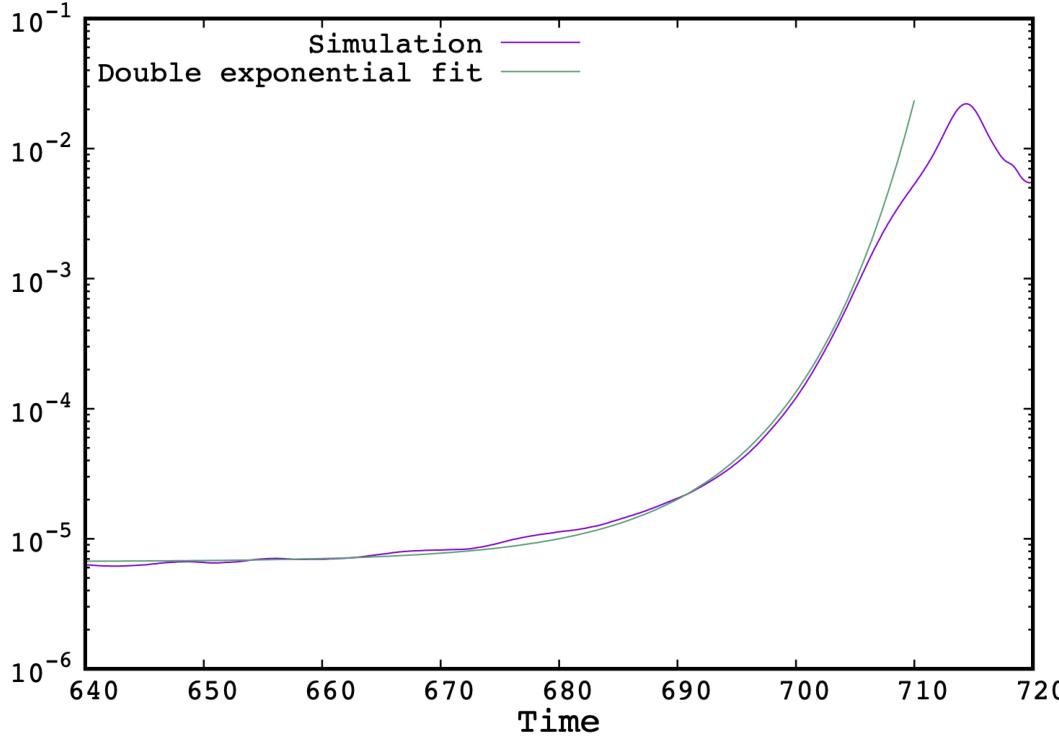
图 7. 代表性“tanh”平衡案例（$a=0.3$、$x_s=0.8$）动能时间演化的局部放大图（聚焦于爆发阶段）。同时绘制了遵循 $\sim \exp [\exp ({\gamma }^{\ast }(t-t_0))]$ 规律的双重指数拟合曲线以供比较，其中 $t_0=688$、${\gamma }^{\ast }=0.1$。

外区的电流密度，或与不同的数值方法有关。因此，仍需进一步研究以深入探讨这一问题。

其次，我们考察了爆发阶段的时间依赖性。如先前研究所示，我们确认了动能 $E_K$ 的超指数增长，其增长速度比简单的指数律更快。此外，我们的结果表明，动能遵循一种双指数形式的增长律：$E_k\sim \exp [\exp ({\gamma }^{\ast }(t-t_0))]$。其中特征参数（称为伪增长率）为 ${\gamma }^{\ast }\simeq 0.1t_A^{-1}$，对应的特征时间尺度与阿尔芬时间相当。

我们的结果对于存在多个电流层的等离子体环境具有重要意义。这类环境广泛存在于多种天体物理等离子体系统中，例如太阳光球、日冕、太阳风以及脉冲星风云。在这些环境中，人们已观测到以突发方式释放磁能的破坏性事件。为解释此类事件的总持续时间，通常需要快于甚至远快于阿尔芬时间尺度的机制。因此，爆发性的非线性DTM机制可能是引发此类破坏事件的一条可能路径。另一条路径则是在电流片中形成等离子体团链（plasmoid chains），当电流层达到非常大的纵横比（即非常长和/或非常薄的电流片）时，至少达到 $\simeq S_L^{1/3}$ 的量级，其中 $S_L=L{V}_A/\eta$（Huang et al. 2017；Baty 2020a,b,c）。这将导致纵横比高于 $10^3–10^4$，远高于本文所考虑的 $L/a$ 值（约为 $10–20$）。在后一种情况下，爆发性重联机制也可被触发，其时间尺度甚至可能小于阿尔芬时间（Pucci & Velli 2014；Comisso et al. 2017）。最后，这两种路径并非互斥，两种机制可能同时起作用（Baty 2017）。无论如何，更贴近实际的研究需要包含两个电流片的初始形成过程，而本文则假设电流片已预先形成。

参考文献

Akramov, T., & Baty, H. 2017, PoP, 24, 082116, https://doi.org/10.1063/1.5000273

Baty, H. 2017, ApJ, 837, 74, https://doi.org/10.3847/1538-4357/aa60bd

Baty, H. 2019, ApJSS, 243, 23, https://doi.org/10.3847/1538-4365/ab2cd2

Baty, H. 2020a, arXiv:2001.07036 https://ui.adsabs.harvard.edu/abs/2020arXiv200107036B

Baty, H. 2020b, arXiv:2003.08660 https://ui.adsabs.harvard.edu/abs/2020arXiv200308660B

Baty, H. 2020c, arXiv:2006.15013 https://ui.adsabs.harvard.edu/abs/2020arXiv200615013B

Biskamp, D. 2009, Nonlinear Magnetohydrodynamics, (Cambridge University Press). https://doi.org/10.1017/CBO9780511599965

Comisso, L., Lingam, L., Huang, Y. M., & Bhattacharjee, A. 2017, ApJ, 850, 142, https://doi.org/10.3847/1538-4357/aa9789

Denisov, S. A. 2015, Proc. Amer. Math. Soc. 143, 1199-1210, https://arxiv.org/pdf/1201.1771.pdf

Huang, Y. M., Comisso, L., & Bhattacharjee, A. 2017, ApJ, 849, 75, https://doi.org/10.3847/1538-4357/aa906d

Ishii, Y., Azumi, M., & Kishimoto, Y. 2002, PRL, 89, 205002, https://doi.org/10.1103/PhysRevLett.89.205002

Kiselev, A., & Sverak, V. 2014, Annals of Mathematics Vol. 180, No. 3, 1205-1220, https://arxiv.org/pdf/1310.4799.pdf

Janvier, M., Kishimoto, M. Y., & Li, J. Q. 2011, PRL, 107, 195001, https://doi.org/10.1103/PhysRevLett.107.195001

Priest, E. R., & Forbes, T. G. 2000, Magnetic Reconnection (Cambridge: Cambridge Univ. Press), https://doi.org/10.1017/CBO9780511525087

Poyé., A., Agullo, O., Smolyakov, A., Benkadda, S., & Garbet, X. 2013, PoP, 20, 020702, https://doi.org/10.1063/1.4791653

Pucci, F., & Velli, M. 2014, ApJL, 780, L19, https://doi.org/10.1088/2041-8205/780/2/L19

Wang, Z. X., Dong, J. Q., Lei, Y. A., Long, Y. X., Mou, Z. Z., & Qu, W. X. 2007, PRL, 99, 185004, https://doi.org/10.1103/PhysRevLett.99.185004

Wei, L., Yu, F., Ren, H. J., & Wang, Z. X. 2010, AIP Advances, 10, 055111, https://doi.org/10.1063/5.0007522

Zhang, C. L., & Ma, Z. W. 2011, PoP, 18, 052303, https://doi.org/10.1063/1.3581064