线束缚对平板几何中电阻撕裂不稳定性的影响
Yiming Huang^{1,2,*} 与 Ellen G. Zweibel^{1,2,3,†}
实验室与天体物理等离子体磁自组织中心,
威斯康星大学麦迪逊分校,威斯康星州 53706
物理系,威斯康星大学麦迪逊分校,威斯康星州 53706
天文学系,威斯康星大学麦迪逊分校,威斯康星州 53706
摘要
本文在约化磁流体力学(RMHD)[1, 2] 框架下研究了线束缚对平板几何中电阻撕裂不稳定性的影响。研究发现,线束缚具有稳定作用。当系统长度 小于某一临界长度 时,撕裂模被稳定,且该临界长度 与电阻率 无关。当 略大于 时,增长率 与 成正比。当 足够长时,系统恢复经典的撕裂模标度律 。从 到 的转变发生在转变长度 处。
I. 引言
线束缚对磁流体力学(MHD)不稳定性影响的研究已有很长的历史。在日冕中,日冕环的磁力线深深锚定(即线束缚)于密度高得多的光球层。长期以来人们认为,由于线束缚的稳定作用,这些环可以比无束缚情况下MHD不稳定性增长时间所预期的稳定得多。Raadu 首次利用能量原理分析了理想内扭曲模的线束缚稳定效应。[3] 此后,针对各种电阻性[4–7]和理想MHD不稳定性[8, 9]开展了更详细的分析。近年来,由于等离子体实验室实验的进展[18, 19],线束缚问题再次引起了理论上的关注。[10–17]
本文研究线束缚对电阻撕裂不稳定性的影响,采用最简单的构型之一——平板几何。平板几何中的撕裂不稳定性在许多教科书中均有讨论。[20, 21] 平衡态是一个简单的电流层,其中电流沿 方向,且电流密度仅依赖于 。与该电流层相关联的是一个磁感应强度 ,其方向在电流层两侧发生反转。该构型在理想情况下是稳定的。引入电阻率后,磁场可通过电阻撕裂不稳定性发生重联。为简化分析,通常假设存在一个强导引磁场(guide field),其方向垂直于重联磁场,从而可采用不可压缩近似。本文所考虑的构型是在导引磁场方向上放置两块理想导体端板,因此是导引磁场被线束缚于端板上。尽管该构型相当简单,但据我们所知,此前尚未有相关研究。Velli 和 Hood 曾研究过平板几何中的线束缚撕裂模,[5] 但在他们的模型中,导体端板垂直于重联磁场。本文所研究的模型可视为基于 Parker 场景的日冕加热模型中更复杂电阻不稳定性的原型。[22–28]
本文其余部分安排如下:第二节建立物理模型和控制方程;第三节讨论从方程中可直接推导出的一些普遍性质,而无需实际求解;第四节简要描述数值方法;第五节给出数值结果;第六节进行总结与结论。
II. 物理模型与控制方程
为简化问题,我们作如下假设:(1) 等离子体密度为常数;(2) 存在一个沿 轴方向的强且恒定的导引磁场;(3) 沿导引磁场方向的长度尺度远大于垂直方向的长度尺度。在此假设下,系统可用著名的约化MHD(RMHD)方程描述。[1, 2] 在该框架下,经适当归一化后,磁场和速度可分别用磁通函数 和流函数 表示为 和 。控制方程为:
其中 和 分别为粘性系数和电阻率; 为垂直梯度; 和 分别为涡量和电流密度; 为泊松括号。这套RMHD方程被广泛用于日冕加热和电流片形成问题的研究。[23–34] 在 处放置两块理想导体端板,以提供线束缚边界条件。尽管线束缚条件是一种理想化假设(因为太阳光球既非完全刚性也非理想导体),但在太阳物理中这是一种常见近似。严格来说,RMHD的尺度排序 与线束缚边界条件不相容,因为在端板附近存在边界层,其中 。然而,Scheper 和 Hassam 通过边界层分析表明,RMHD 仍可用于日冕区域,因为边界层仅在计算 的高阶修正时才出现,而 的高阶修正与 和 完全解耦。[35]
我们假设平衡态仅依赖于 ,即 。考虑如下形式的扰动: 和 。将RMHD方程线性化后得到:
其中 ,撇号表示对 的导数。在RMHD近似下,线束缚边界条件简化为在 处 。本文将聚焦于惯性撕裂模;此后全文均假设粘性 。
III. 解析分析
尽管线性化方程难以解析求解,但通过解析分析仍可推导出一些普遍性质。首先,假设存在一个临界长度 ,使得 。令 并将 按 重新标度(即 ),方程 (3) 和 (4) 变为:
边界条件为 。方程 (5) 和 (6) 可视为以 为本征值的本征值问题。进一步注意到,若令 ,参数 将完全从方程中消去。因此我们得出结论:临界长度 与 无关。需注意以下几点:(1) 的存在性并非必然;(2) 边际稳定性未必发生在 处,因为方程并未排除纯振荡模的可能性。在考虑这些注意事项的前提下,我们通过数值计算发现 确实存在,且确实与 无关。
现在考虑一个略偏离边际稳定性的不稳定系统,即 。若不稳定模的增长极其缓慢,可忽略方程 (3) 中的惯性项(即左边项)。物理上,这意味着整个区域内系统始终保持无力场(force-free)状态。忽略方程 (3) 中的惯性项,并将方程 (4) 除以 ,可得无力场近似下的方程:
由此立即可得,在无力场近似下,增长率 和流函数 均按 标度。由于惯性项 ,预期该近似在 足够小时成立。
无电流近似(force-free approximation)在其他条件不变的情况下,对于更小的 效果更好。回顾一下,在周期性系统中,磁场仅在“外层”区域(即远离共振面 的区域)近似满足无电流条件。在内层区域,电阻率和惯性效应均需考虑。内层厚度 ,因此增长率 。[36, 37] 自然地,如果系统足够长,我们预期会恢复 的标度关系。关键问题是:这种转变发生在什么系统长度?我们将在后文讨论这一问题。
最后,我们简要说明边界条件。方程 (3) 和 (4) 分别是关于 和 的一阶微分方程(对 求导),因此需要两个边界条件。我们对 有两个边界条件 ,而对 则没有边界条件。若给定 ,则可沿 方向积分方程 (4) 以求解 。一般而言,如此得到的 无法同时满足两个边界条件,除非 满足某种可解性条件。对方程 (4) 两边乘以 并在区间 上积分,再通过分部积分并利用 的边界条件,可得如下可解性条件:
本文后续部分并未使用该可解性条件,但我们曾用它来检验数值解的准确性。
IV. 数值方法
我们采用的数值方法可视为 Evstatiev 等人在文献 [14] 中提出方法的一种变体。本质上,这是一种二维打靶法(shooting method)。我们可以将方程 (3) 和 (4) 重写为沿 方向的演化方程:
其中算符 定义为(设 ):
从 处的初始条件 出发,可利用方程 (10) 沿 方向推进该初始条件。形式上,解可写为:
显然, 是一个本征值,当且仅当存在某个 处的初始条件,使得通过方程 (12) 推进到两端面后满足边界条件。在当前情形下,我们可考虑如下线性映射:
为简化记号,下文我们将用 表示初始条件。为满足边界条件,需满足:
其中 为某种合适的范数。此处我们采用通常 范数的直接推广:
现在,若给定系统长度 ,可在整个复 平面上扫描 。那些使 的 即为本征值。或者,也可固定 ,扫描 以找出使该 成为本征值的系统长度。
为在数值上实现这一思想,首先需要对算符 构造高精度的离散近似。拟谱方法(pseudospectral methods)适用于此任务。[38–40] 方程 (15) 和 (16) 中的数值积分采用高斯求积法(Gaussian quadrature)完成。[41, 42] 由于我们处理的是无限域(如大多数教科书所述),需将 光滑映射到 以应用拟谱方法。我们采用如下映射方式:[43] 首先,
将 映射到 。然后进行第二次映射:
将 映射到 。该映射可进一步在 附近集中分辨率,以解析电阻层。常数 、、 为自由参数。我们在 上设置 个勒让德-高斯配置点(Legendre-Gauss collocation points)[40]。首先在这些节点上计算关于 的微分矩阵和高斯求积权重,再将其变换回 坐标。在此离散近似下,初始条件 由列向量 表示,其元素为配置点上的 和 。算符 和 分别由矩阵 和 表示。范数表示为:
其中 表示共轭转置, 为来自高斯求积的实对角矩阵。我们需要求解:
以及对应的使该式取最小值的 。令 且 ,则:
现在我们计算奇异值分解(SVD)[42]:,其中 和 分别为左、右奇异向量的酉矩阵, 为非负实对角矩阵,其对角元为奇异值。此时 即为最小奇异值,而 ,其中 为对应最小奇异值的右奇异向量(即 的一列)。通过 沿 方向推进 ,即可重构本征函数。
图1展示了在复数 域内、参数为 、 时的 。那些使 趋近于零的 值即为本征值。在此特定情形下,我们在该域内找到了六个本征值,且全部位于实轴上。扫描整个复数域在计算上代价较高。幸运的是,我们发现最不稳定的模态总是具有实本征值。因此,在大多数计算中,我们仅沿实轴进行扫描。
此处我们简要将我们的方法与 Evstatiev 等人在文献 [14] 中提出的方法进行比较。这些作者在方程 (10) 中令 (他们使用 代替 ),然后将其作为辅助本征值问题求解。设 ,其中 是 的本征值, 是对应的本征函数。通解可写为 (截断为有限项 个模态),该解满足方程 (10)。为施加边界条件,他们考虑
其中 象征性地表示解(在当前情形下仅指 部分)在端板上 个点(可任意选取,且 )处的取值。通过在给定 下扫描 (或在给定 下扫描 ), 的局部极小值对应于原始本征值问题的一个本征模态。现在可以清楚地看出,这两种方法非常相似,差异仅在于一些细节。如果 的本征模态构成完备基,则投影到该本征基上是求解 的一种便捷高效的方式。具体而言,若 ,则 。与其用配置点上的值表示 ,不如使用展开系数 。线性映射 、范数 以及 也可类似地用 定义。以这种方式表述,我们的方法与他们的方法几乎完全相同。两者之间唯一的实质性区别在于我们使用 而非 。然而值得指出的是,即使 的本征模态不完备, 仍可能存在。 因此,我们的方法并不依赖于完备本征基的存在。
的优势在于其具有精确的解析定义,即方程 (14);而方程 (20) 仅是对其的数值近似。这使我们能够更方便地检验收敛性——若数值解完全收敛,则 应与分辨率和映射参数无关。另一方面, 的定义依赖于用于施加边界条件的点集、用于展开的本征模态集 以及本征模态的归一化方式。图2展示了针对分辨率 、、 的收敛性测试结果。 的计算给出 ,而另外两次计算给出 。注意 和 的曲线几乎完全重合,表明已收敛。对于 的计算,结果与 的曲线实际上无法区分。图3展示了相同计算得到的本征函数 。尽管 计算所得本征值的相对误差仅约为 0.2%,但其本征函数显然不够准确。 的结果已有显著改善,但虚部仍存在振荡。 的计算则给出了完全收敛的本征函数。这再次表明,获得精确的本征函数远比获得本征值困难。为确保本文所有数值结果均完全收敛,我们付出了大量努力。
V. 结果
我们采用 Harris 电流片 (其中 )作为平衡态。大多数计算采用波数 。对 的依赖性将在后文讨论。
A. 周期性系统
周期性系统通常针对 的情形求解,但该分析可轻易推广至 的情形。在所谓的恒定 近似下(即在电阻层内 近似为常数),增长率 与 成正比。[36, 37] 图4展示了不同 下 随 的变化关系。在渐近极限 下,所有曲线应彼此重合。可立即观察到一些有趣特征:(1) 除 外, 并非增长率的峰值。正如后文将看到的,这对线系解具有有趣的影响。(2) 的标度律在 附近效果更好。这可能是因为在该处更容易满足恒定 近似。然而,我们预期只要 足够小,恒定 近似最终将适用于所有 。
乍看之下, 是 的局部极小值似乎有违直觉。在撕裂模分析中, 由共振面上的 和 决定。对于 Harris 电流片剖面,当 时 难以解析计算。然而,对于类似的分段线性剖面(即当 时 ,当 时 ),可求得解析的 。可以证明,在此情形下 同样是局部极小值。事实上,当 时 发散。这种病态行为可能源于 处 的突变,这是非物理的。然而,这一简单系统的结果表明,对于我们所考虑的系统, 为局部极小值可能是普遍现象,或至少并不令人意外。
B. 线系系统
图5总结了不同 下最快增长模态的增长率 随 的变化关系。图中我们将 对 进行了归一化。如第三节所述,我们预期临界长度 与 无关,且在临界点附近 与 成正比。数值计算结果证实了这两点。发现对所有 均有 ,且 与 的关系曲线均与无力场近似下的预测一致。当 增大时,曲线开始偏离无力场近似,且 越大,偏离发生得越早。这也符合第三节的预期。水平条带表示由周期性系统在 处的 与最大周期性 (见图4)所确定的范围。我们观察到,当增长率偏离无力场近似时,首先会超过 处的周期性 ,最终趋于(但永不超越)最大周期性 。因此,无力场近似和最大周期性增长率可视为线系增长率的两个渐近线。当 和 的情形趋近其周期性极限时,我们未能获得完全收敛的结果。然而,基于较大 情形的观察,可以相当有把握地认为双渐近线方案具有普适性。
图6和图7展示了 时不同 下的本征函数 和 。本征函数已归一化,使得 。在临界长度 处,本征函数非常光滑。随着 增大, 处的内层变得越来越陡峭。直至 ,本征函数仍基本覆盖整个 方向长度。在 和 时,本征函数局域于中平面附近,这种局域化在 中更为显著。在 时,增长率已超过 处的周期性增长率。内层“分裂”为两部分,且沿 方向出现振荡。这是由于周期性系统的色散关系具有特殊的双峰结构(图4)。在周期性系统中, 对应四个非零 值,因此我们预期线系模态将主要由 的行为主导。这四个周期性模态在四个不同位置具有共振面,形成两对:一对位于 ,另一对位于 。这两对共振面大致对应于分裂内层的两部分。根据文献 [14–16] 的讨论,当每对内的两个共振面足够接近时,用 的四个本征模态展开将是一个良好的近似。
然而,我们发现要实现这一点需要极大的 ,在此区域内我们难以获得完全收敛的结果。
作为对比,图8展示了与图6参数相同但采用无力场近似的本征函数 。 时的无力场近似与真实解几乎完全相同。即使在 时,无力场解与真实解仍相差不大。但在 及以上时,两者差异显著。从图5也可得出相同结论:无力场色散关系在 以内效果良好,之后开始偏离真实解。我们还观察到,无力场本征函数的内层随 增大而持续变陡。图9展示了不同 下 Im() 的中平面截面,图10展示了其无力场对应结果。两图中还给出了包含惯性项的 周期性本征模态作为参考。注意在周期性系统中,必须包含惯性项才能解析内层,[36, 37] 而在线系构型中,仅靠边界条件(无 奇异性)即可解析内层。遵循文献 [16] 的惯例,无力场近似的内层宽度称为“几何”宽度,而周期性本征模态的内层宽度称为“撕裂”宽度。在 时,几何宽度约等于撕裂宽度,这正是无力场近似即将失效的时刻。
因此,我们得出结论:当惯性项不再可忽略,或等价地,当撕裂宽度与几何宽度相当时,增长率将从电阻标度律 过渡到撕裂标度律 。这促使我们进行类似于文献 [16] 的标度分析。假设恒定 近似,并令 为内层厚度,则在层内有 ,,以及 ,其中 定义为 在层两侧的跃变除以 。[36, 37] 对于周期性情形,在层内有 和 。即
由此可得撕裂增长率
以及撕裂宽度
对于采用无力场近似的线系情形,由于本征函数遍布整个长度(图8),可假设 。在内层内,有 ;即几何宽度为
由感应方程可得
此外,可由 估算 :
若满足 ,即 ,则无体力近似是自洽的。利用式 (27)、(28) 和 (29),该自洽条件可写为
其中 是从电阻标度过渡到撕裂标度的过渡长度。若要求 ,也可得到相同的条件。
标度分析预测过渡长度 。同时我们知道,当 变大时,。这促使我们以下述方式重新标度图 5:绘制 与 的关系。将 除以 可使渐近区域处于同一水平,而将 乘以 则使过渡长度落在同一位置。结果如图 11 所示。显然,不同 对应的曲线彼此接近,尤其是较小 的曲线几乎完全重合。因此,数值结果与 的预测一致。分析还预测 。从图 5 可以看出,无体力色散关系非常接近一条直线,这表明我们可以将斜率与 联系起来。对于 Harris 电流片位型,。为验证这一猜想,我们需要对不同的 求出斜率。不同 对应的斜率和临界长度总结于表 II 中。我们发现 对 的依赖很弱。将斜率拟合为 ,得到斜率 。如图 12 所示,这是一个极佳的拟合。
| Slope | |||
|---|---|---|---|
| 0.3 | 112.85 | 0.0288 | 0.182 |
| 0.4 | 111.50 | 0.0266 | 0.168 |
| 0.5 | 115.09 | 0.0239 | 0.150 |
| 0.6 | 123.86 | 0.0204 | 0.128 |
| 0.7 | 141.09 | 0.0162 | 0.102 |
表 II:不同 下的临界长度 以及无体力色散关系 对 的斜率。同时列出对应的 。标度分析表明斜率 。
VI. 总结与讨论
本文详细研究了磁力线钉扎效应对电阻撕裂不稳定性的影响。我们发现磁力线钉扎具有稳定作用,只有当系统长度大于一个与电阻率 无关的临界长度 时,才会发生不稳定性。当系统长度不太长时,等离子体惯性可忽略不计,即在整个区域内等离子体近似处于无体力状态。在此区域内,增长率 与 成正比,且不稳定模的内层宽度远大于周期性情形下的宽度。当系统长度足够长时,可恢复撕裂模标度 。从 到 的过渡发生在电阻层内等离子体惯性不再可忽略之时,这也正是“几何”宽度与“撕裂”宽度相当的时候。过渡长度 的标度为 。
从物理上理解,在无体力近似下增长率与 成正比并不困难。在原始系统中存在两个时间尺度:阿尔芬时间尺度和电阻时间尺度;撕裂模的增长发生在两者的混合时间尺度上。若完全忽略惯性,则只剩下电阻时间尺度,因此模只能在电阻时间尺度上增长。然而,只有在磁力线钉扎系统中才可能在整个区域内忽略惯性,因为钉扎边界条件可用来消除有理面处的奇异性。而在周期性系统中,惯性项总会在有理面附近起作用。
周期性增长率与无体力近似下的增长率可视为磁力线钉扎增长率的两个渐近极限。无体力增长率 近似与 呈线性关系,其斜率与 有关。在非常好的近似下,,其中 在 处取值。遗憾的是,我们尚无好的方法来估算临界长度 。
在很大程度上,我们的发现与 Delzano 和 Finn 早期在柱坐标系中的研究一致。[15] 一个主要差异在于,我们发现 ,而他们报告的是 (他们实际上针对给定的 考察了交叉电阻率 ,并发现 ;但这只是固定哪个变量的问题)。造成差异的一个可能解释是,他们在参数变化时使用了相当大的粘性且保持不变。我们尚未详细研究粘性的影响。一些初步结果表明,粘性确实有显著影响,当加入大粘性时, 的标度不再成立。
最后,我们简要讨论这些发现对日冕的适用性。日冕具有极高的电导率,观测到的日冕环的纵横比为 10–100,远小于撕裂模增长所需的尺度。因此,电阻不稳定性很可能运行在 的区域。一个直接的问题是:既然日冕中的电阻时间尺度如此之长,电阻不稳定性是否还有意义?目前我们尚无明确答案。显然,我们的模型高度理想化,存在一些明显的不足。一个直接的担忧是,我们的分析未包含足点驱动;因此平衡位型将在电阻时间尺度 上衰减。我们的分析隐含地假设了 (从而可忽略电阻衰减),或假设平衡由某种外部电流驱动维持(如实验室装置中那样)。在日冕中,电流由足点运动驱动,当 时,这一假设显然不成立,因为此时增长率 与 相当甚至更小。解决此问题的一个方法是在系统中加入足点驱动以维持平衡。这将给平衡态引入一个整体背景流,并可能对稳定性产生一定影响,尤其是在系统接近临界稳定时。详细的分析留待未来研究。此外,我们为简化而采用的刚性壁边界条件可能过于严格,正如一些研究者所指出的那样。这一点在考虑 的模时尤为明显,因为在缓慢的增长时间尺度上,光球层可能能够作出响应。恰当的处理需要对光球层内部有更详细的了解。[7, 44–46] 鉴于这些不足,我们的发现在应用于日冕时显然需要进一步检验。
最后需要指出的是,必须研究该模的非线性演化。事实上,即使在无磁力线钉扎的经典撕裂模理论中,不稳定模也会迅速进入非线性区域。[47] 我们的初步研究表明,随着模的非线性演化,原始电流层内可形成细丝状电流结构。因此,电阻不稳定性在电流片变薄过程中所起的作用不容忽视。另一个有趣之处在于,由于稳定性判据与电阻率无关而增长率却与之相关,日冕可能看似平静,实则已处于不稳定构型。电阻不稳定性缓慢的增长率使得日冕可被驱动至远超临界点的状态,从而储存更多自由能。然而,无论多么缓慢,电阻不稳定性仍为日冕提供了一种途径,使其能够从理想情况下稳定的构型中释放自由能。电阻不稳定性在此可能扮演的多重角色值得深入思考。我们希望在未来能探讨其中一些问题。
致谢
我们很高兴感谢 G. L. Delzano 博士、E. G. Evstatiev 博士和 J. M. Finn 博士就其数值方法及磁力线钉扎物理所进行的有益讨论。黄一民感谢 Daniel Lecoanet 和 Nick Murphy 的启发。黄一民还感谢 A. Bhattacharjee 教授支持其在美国物理学会等离子体物理分会年会上报告本工作。作者们衷心感谢审稿人富有洞察力的意见。本研究由美国国家科学基金会资助,项目编号 PHY-0215581(PFC:实验室与天体物理等离子体中的磁自组织中心)。
[3] M. A. Raadu, Solar Physics 22, 425 (1972).
[4] M. Velli and A. W. Hood, Solar Physics 106, 353 (1986).
[5] M. Velli and A. W. Hood, Solar Physics 119, 107 (1989).
[6] M. Velli, A. W. Hood, and G. Einaudi, Astrophys. J. 350, 419 (1990).
[7] A. B. Hassam, Astrophys. J. 348, 778 (1990).
[8] M. Velli, A. W. Hood, and G. Einaudi, Astrophys. J. 350, 428 (1990).
[9] E. G. Zweibel and D. L. Bruhwiler, Astrophys. J. 399, 318 (1992).
[10] C. C. Hegna, Phys. Plasmas 11, 4230 (2004).
[11] D. D. Ryutov, R. H. Cohen, and L. D. Pearlstein, Phys. Plasmas 11, 4740 (2004).
[12] D. D. Ryutov, I. Furno, T. P. Intrator, A. S., and T. Madziwa-Nussinov, Phys. Plasmas 13, 032105 (2006).
[13] Y.-M. Huang, E. G. Zweibel, and C. R. Sovinec, Phys. Plasmas 13, 092102 (2006).
[14] E. G. Evstatiev, G. L. Delzanno, and J. M. Finn, Phys. Plasmas 13, 072902 (2006).
[15] G. L. Delzanno, E. G. Evstatiev, and J. M. Finn, Phys. Plasmas 14, 072902 (2007).
[16] G. L. Delzanno 和 J. M. Finn, Phys. Plasmas 15, 032904 (2008)。
[17] V. A. Svidzinski, V. V. Mirnov 和 H. Li, Phys. Plasmas 15, 092106 (2008)。
[18] W. F. Bergerson, C. B. Forest, G. Fiksel, D. A. Hannum, R. Kendrick, J. S. Sarff 和 S. Stambler, Phys. Rev. Lett. 96, 015004 (2006)。
[19] X. Sun, T. P. Intrator, L. Dorf, I. Furno 和 G. Lapenta, Phys. Rev. Lett. 100, 205004 (2008)。
[20] R. J. Goldston 和 P. H. Rutherford, 《等离子体物理导论》(Institute of Physics Publishing, Philadelphia, 1995)。
[21] P. A. Sturrock, 《等离子体物理:天体物理、地球物理与实验室等离子体理论导论》(Cambridge University Press, 1994)。
[22] E. N. Parker, Astrophys. J. 174, 499 (1972)。
[23] P. Dmitruk, D. O. Gómez 和 E. E. DeLuca, Astrophys. J. 505, 974 (1998)。
[24] P. Dmitruk 和 D. O. Gómez, Astrophys. J. 527, L63 (1999)。
[25] P. Dmitruk, D. O. Gómez 和 W. H. Matthaeus, Phys. Plasmas 10, 3584 (2003)。
[26] A. F. Rappazzo, R. B. Dahlburg, G. Einaudi 和 M. Velli, Advances in Space Research 37, 1335 (2006)。
[27] A. F. Rappazzo, M. Velli, G. Einaudi 和 R. B. Dahlburg, Astrophys. J. 657, L47 (2007)。
[28] A. F. Rappazzo, M. Velli, G. Einaudi 和 R. B. Dahlburg, Astrophys. J. 677, 1348 (2008)。
[29] D. W. Longcope 和 R. N. Sudan, Astrophys. J. 384, 305 (1992)。
[30] D. W. Longcope 和 R. N. Sudan, Phys. Rev. Lett. 68, 1706 (1992)。
[31] D. W. Longcope 和 R. N. Sudan, Phys. Fluids B-Plasma Phys. 4, 2277 (1992)。
[32] D. W. Longcope 和 H. R. Strauss, Astrophys. J. 437, 851 (1994)。
[33] D. W. Longcope 和 R. N. Sudan, Astrophys. J. 437, 491 (1994)。
[34] C. S. Ng 和 A. Bhattacharjee, Phys. Plasmas 5, 4028 (1998)。
[35] R. A. Scheper 和 A. B. Hassam, Astrophys. J. 511, 976 (1999)。
[36] H. P. Furth, J. Killeen 和 M. N. Rosenbluth, Phys. Fluids 6, 459 (1963)。
[37] R. B. White, Rev. Mod. Phys. 58, 183 (1986)。
[38] L. N. Trefethen, 《MATLAB中的谱方法》(SIAM, Philadelphia, 2000)。
[39] W. J. A. C. 和 S. C. Reddy, ACM Trans. Math. Softw. 26, 465 (2000)。
[40] B. Fornberg, 《拟谱方法实用指南》(Cambridge University Press, 1995)。
[41] W. H. Press, S. A. Teukolsky, W. T. Vetterling 和 B. P. Flannery, 《C++数值方法:科学计算的艺术》(Cambridge University Press, 2002),第2版。
[42] L. N. Trefethen 和 D. Bau, III, 《数值线性代数》(SIAM, Philadelphia, 1997)。
[43] J. P. Boyd, 《切比雪夫与傅里叶谱方法》(Dover Publications, Inc., 2001),第2版。
[44] A. W. Hood, Solar Physics 105, 307 (1986)。
[45] R. A. M. van der Linden, A. W. Hood 和 J. P. Goedbloed, Solar Physics 154, 69 (1994)。
[46] E. G. Zweibel, Geophys. Astrophys. Fluid Dyn. 32, 317 (1985).
[47] P. H. Rutherford, Phys. Fluids 16, 1903 (1973).
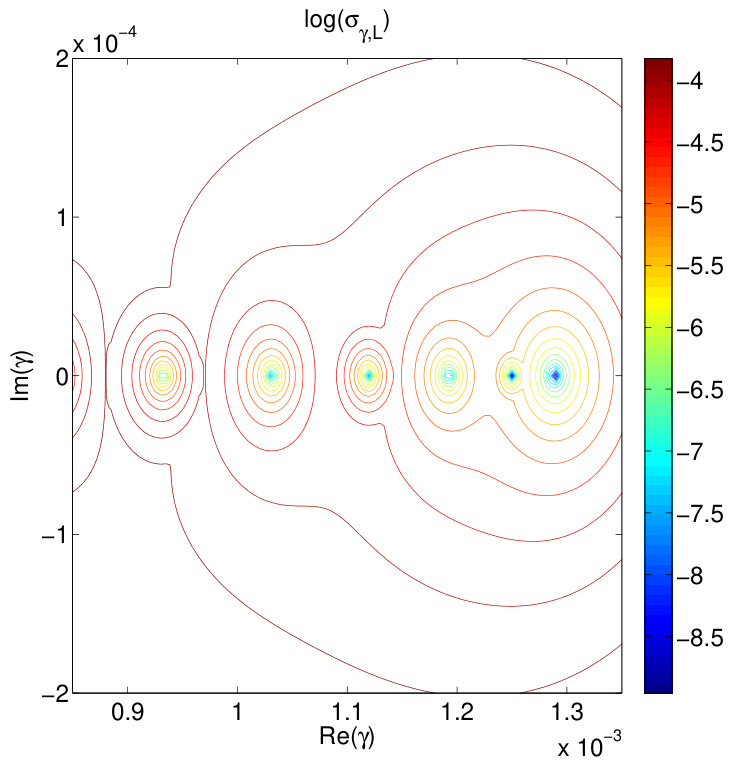
图1:(彩色在线)在复平面 的某一区域内 的分布。其中 ,。 趋近于零的那些 值即为本征值。在此区域内我们找到了六个本征值,它们全部位于实轴上。
图2:(彩色在线)针对 、 情况下的收敛性测试。映射参数为 、、。 的计算给出 ,而另外两次计算给出 。注意, 与 计算得到的曲线几乎完全重合,表明结果已收敛。对于 的计算,结果与 的曲线实际上已无法区分。
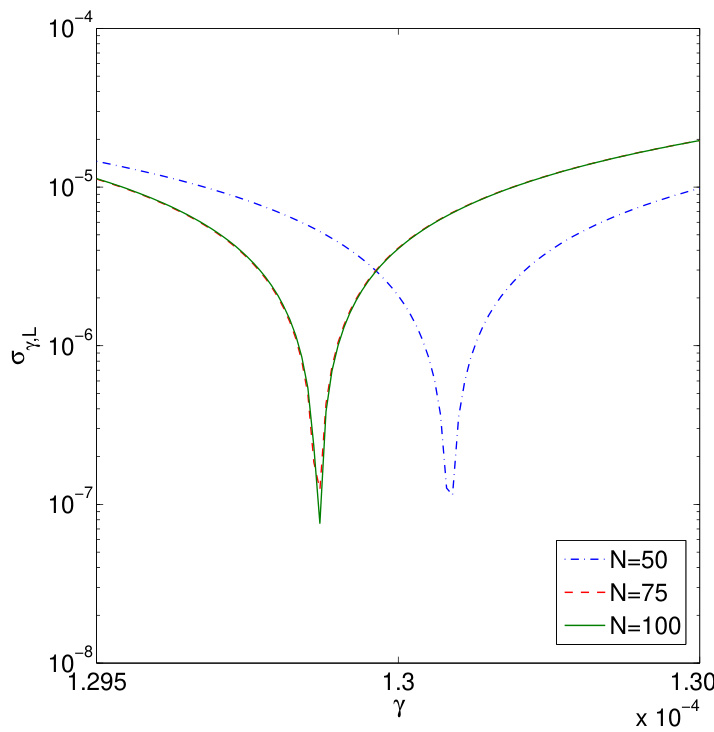
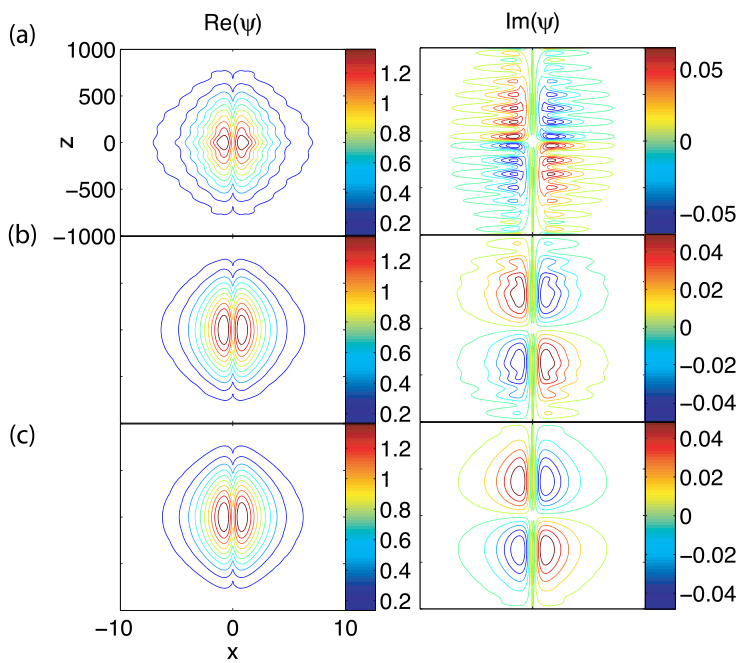
图3:(彩色在线)图2所示收敛性测试中本征函数 的实部与虚部。(a),(b),(c)。注意,尽管 计算所得本征值的相对误差仅为约 0.2%,但其本征函数显然不够精确。 的结果已有明显改善,但虚部仍存在振荡。 的计算给出了完全收敛的本征函数。
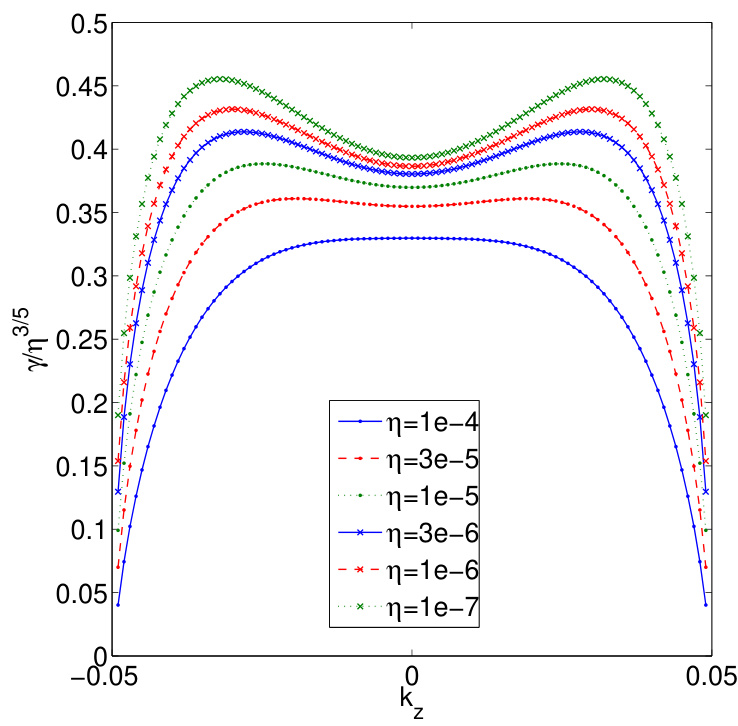
图4:(彩色在线)周期性系统中 随 的变化关系。
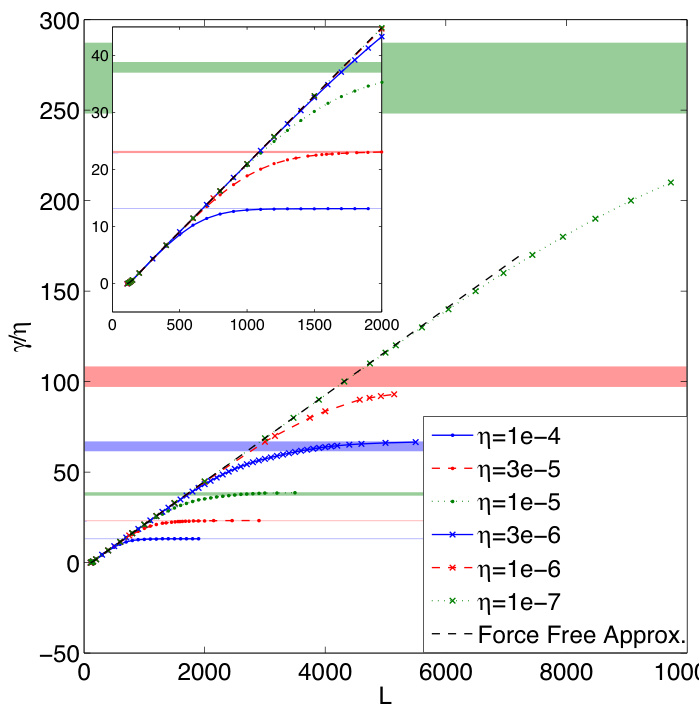
图5:(彩色在线)不同 下 随 的变化关系。水平条带表示由 处的周期性 与最大周期性 (见图4)所确定的范围。虚线为无电流近似(force-free approximation)的预测结果。插图:左下角区域的放大视图。
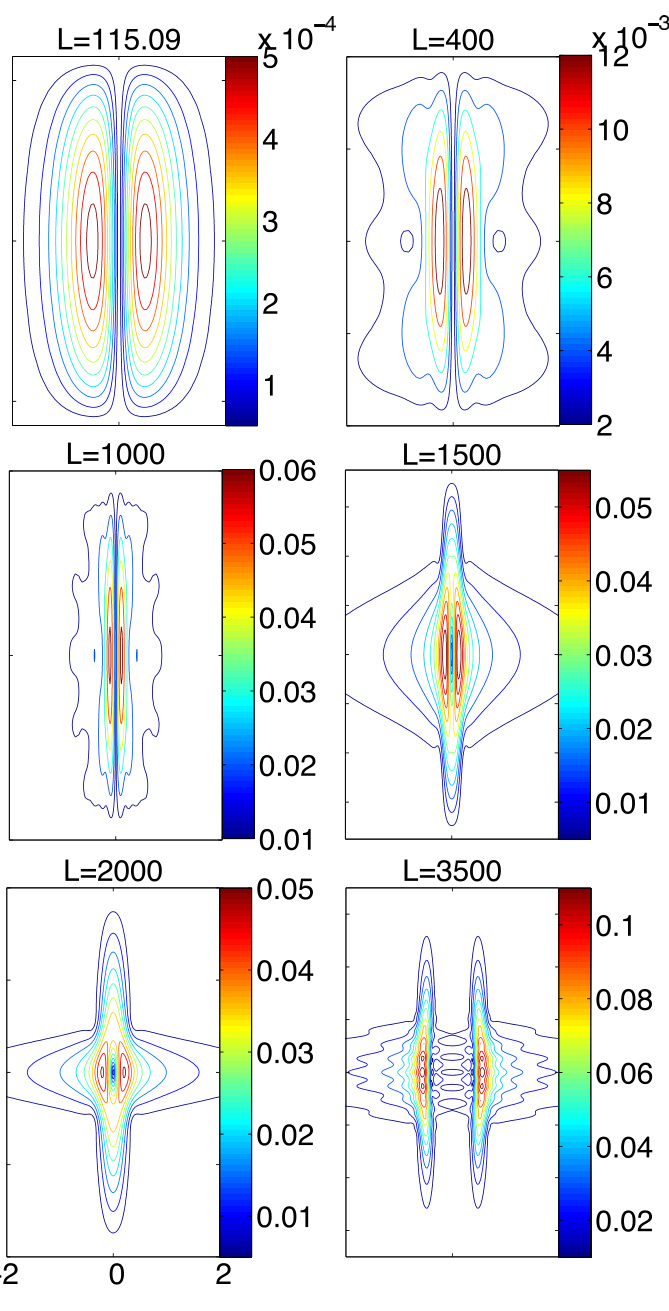
图6:(彩色在线)不同 下的本征函数 。。
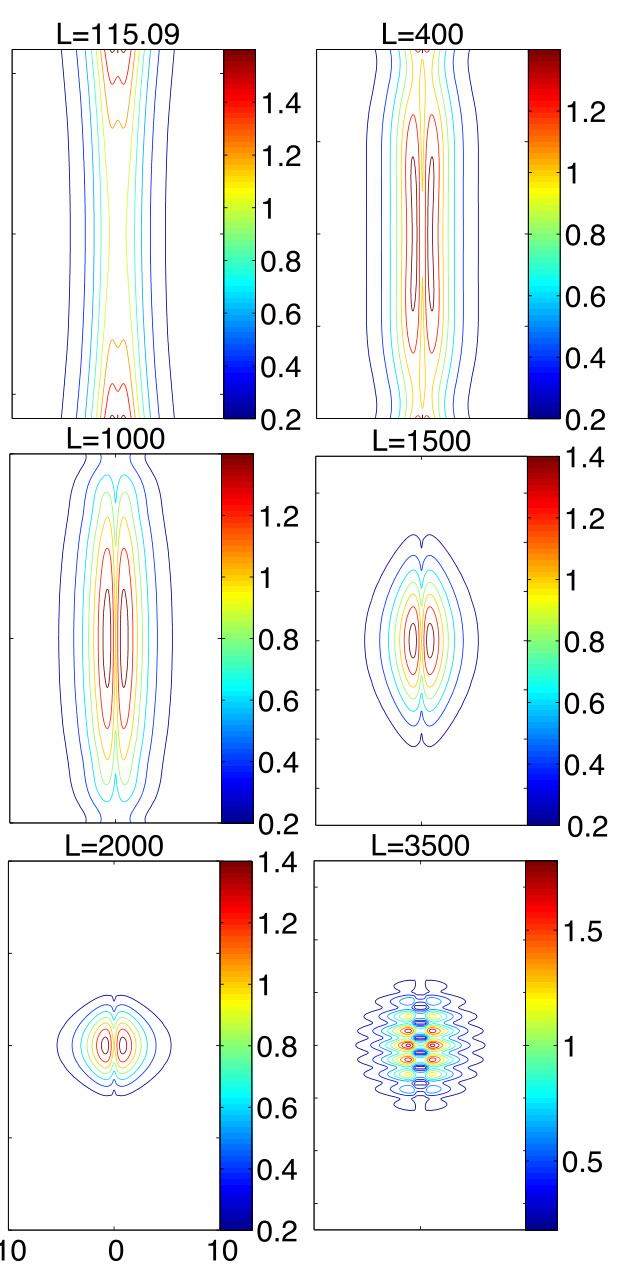
图7:(彩色在线)不同 下的本征函数 。。
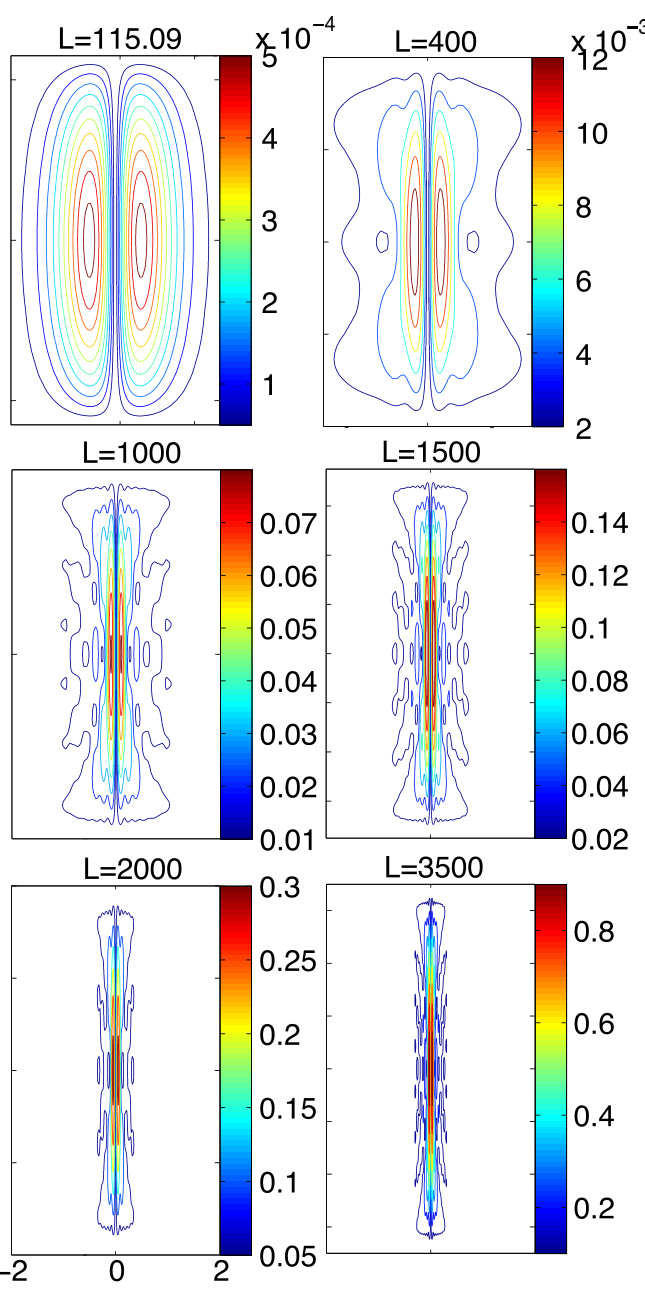
图8:(彩色在线)无电流近似下不同 的本征函数 。。
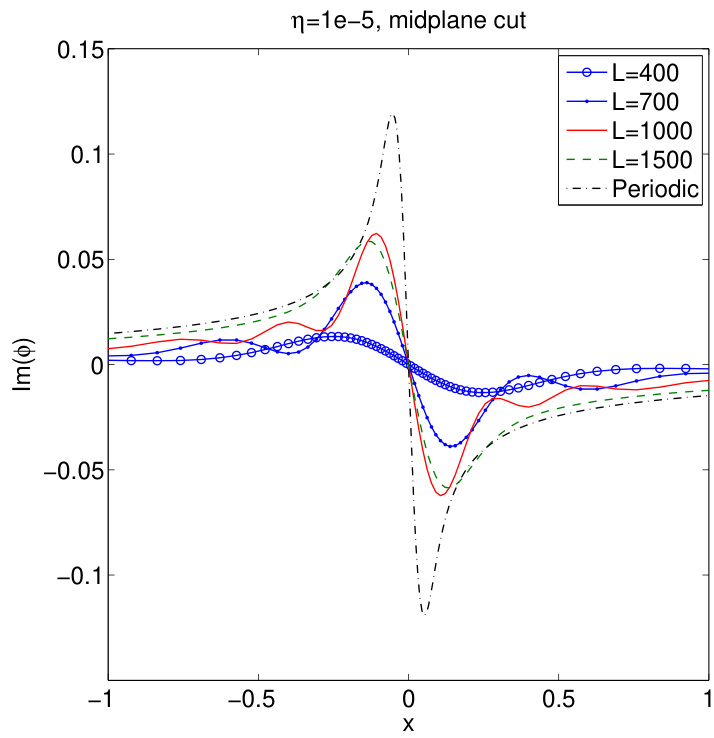
图9:(彩色在线) 虚部在中平面的截面。图中同时给出了 的周期性解作为参考。
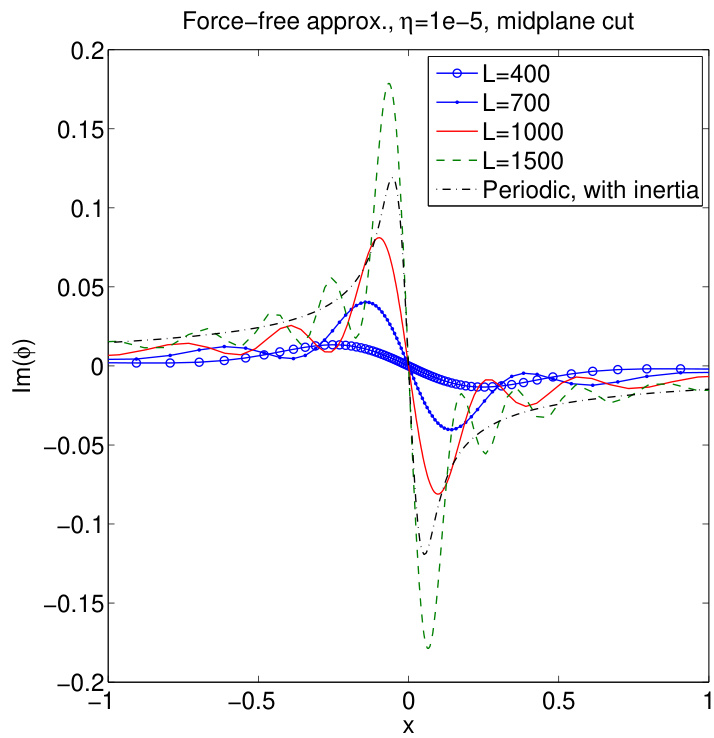
图10:(彩色在线)无电流近似下 虚部在中平面的截面。图中同时给出了 的周期性解(含惯性效应)作为参考。
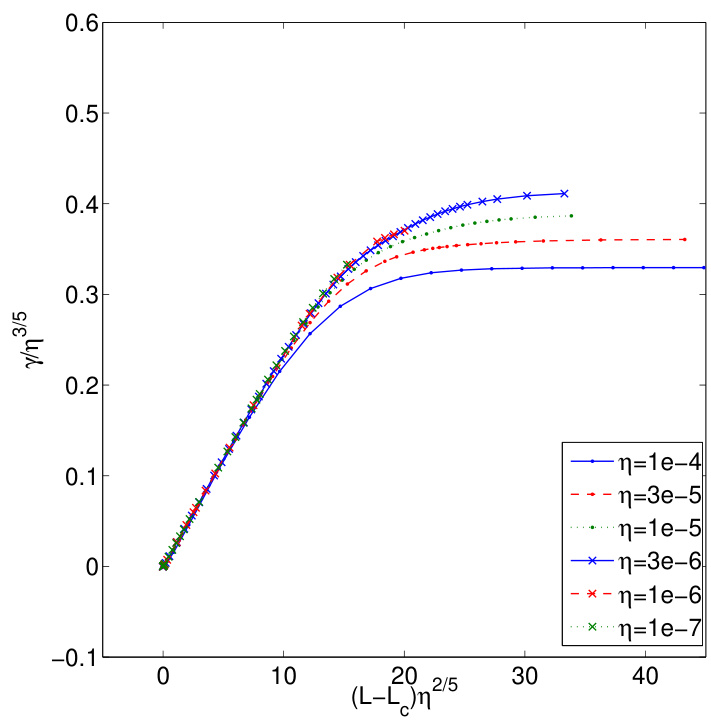
图11:(彩色在线)经重新标度后的线系(line-tied)增长率随 的变化关系。
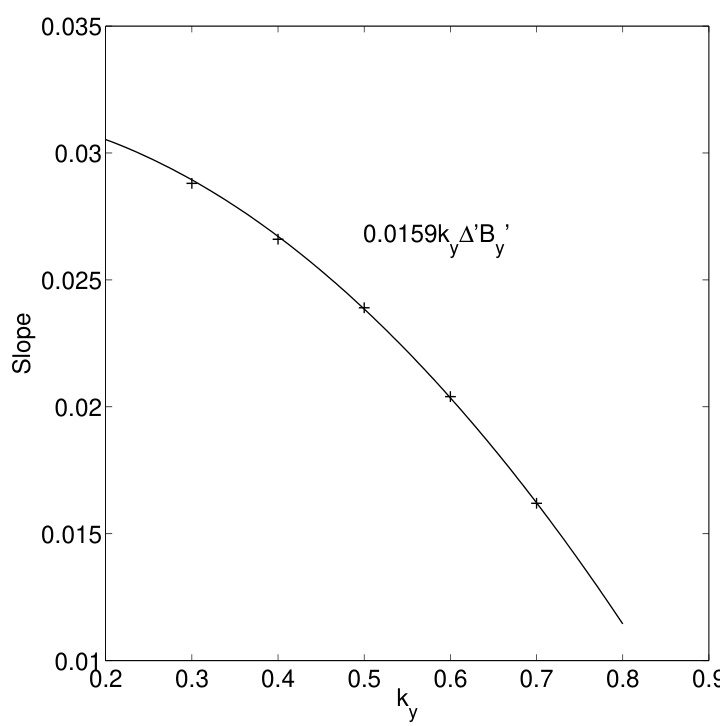
图12:不同 下无电流近似中 与 关系曲线的斜率(该曲线近似为直线)。曲线 与数值结果高度吻合。