反场箍缩中磁岛的演化方程
致谢
非常荣幸能向所有使本论文得以完成的人致以诚挚谢意。首先,我要衷心感谢 Richard Fitzpatrick。他在物理直觉、精妙的近似处理技巧,以及几乎随时(99.9%的时间)愿意与我讨论问题等方面的帮助,对我穿越等离子体物理这片丛林起到了不可估量的指导作用。此外,他还是个好人。谢谢你,Richard。
我也要感谢我的委员会成员:Roger Bengtson 总是给予我很好的建议;Gary Hallock 尽管已有四年未曾谋面,仍同意担任我的委员;Richard Hazeltine 不仅撰写了优秀的《等离子体约束》一书,还提供了诸多有益建议;Phil Morrison 则以其敏锐的评论以及带我参观他那宏伟住宅的经历让我受益匪浅。
我还要特别感谢 Ping Zhu,他在最后那些艰难而痛苦的关头给予了我极大的帮助。而且,在那些深夜时分,能在楼里看到另一位人类也是一件令人欣慰的事。
非常感谢我现在的办公室室友 Bo Hu,他是 Adobe Illustrator 的大师;同时也要感谢我的研究生同学们以及曾经的办公室室友们,感谢他们的友谊与支持:Sergey、Koichi、Evstati、Tom、Chris(Jones 和 Crabtree)、Enrico、Andrew、Bernhard、Nikhil、Dave 和 Kurt。
我也要感谢系里的“粘合剂”——各位秘书们,感谢她们亲切的帮助和出色的工作:Carolyn、Saralyn、Dawn、Suzy 和 Norma。
尽管他们某种程度上导致了我研究生生涯的延长,我还是要感谢 Zilker 和 Aussie's 的朋友们,感谢那些精彩的沙排比赛。
谢谢妈妈、爸爸,还有 Robert。同时也要感谢我那些了不起的朋友(也是曾经的室友)Steve、Todd、Gil 和 Neal。
最后,但绝非最不重要的是,我要感谢Nicole Bodor,没有她的爱与耐心,我绝不可能走到今天。
摘要
我们推导出一组耦合方程,包括一个偏微分方程(PDE)和若干常微分方程(ODE),用于描述反场箍缩(RFP)中非线性磁岛链的相位演化,该演化受到电阻真空容器中感应涡流产生的制动转矩以及外部共振磁扰动(RMP)引起的锁定转矩的影响。我们首先利用所得到的相位演化方程研究磁岛链的锁定行为;此类研究具有重要意义,因为撕裂模及其相关的磁岛会形成环向局域化的磁结构(即“slink模”),若该结构被静态RMP锁定,将严重劣化等离子体约束性能。我们分析中的一个关键步骤是将原始的PDE/ODE相位演化描述简化为一组更为简洁且物理图像清晰的一阶耦合ODE,其新颖之处在于:与磁岛链共同旋转的等离子体区域的径向范围由粘性效应自洽地确定。利用这些方程,我们建立了关于电阻真空容器对误差场锁定与解锁阈值影响的完整理论。
我们的ODE相位演化描述存在一定局限性,即无法描述磁岛宽度的演化或RMP的时间变化。因此,我们的最后一步工作是扩展上述简化的相位演化方程,使其与一个(类似Rutherford方程的)磁岛宽度演化方程耦合,从而能够完整描述在具有可编程幅度和频率波形的旋转RMP作用下磁岛链的动力学行为。因此,我们可以利用这些磁岛演化方程对磁反馈实验进行建模。
第 1 章 引言
国际磁约束聚变计划已持续50多年,其目标是开发一种清洁且取之不尽的能源。然而,这一目标的进展在很大程度上受到等离子体不稳定性的影响。其中最快(也最危险)的一类不稳定性是理想磁流体力学(MHD)不稳定性,它能在几微秒的时间尺度内迅速破坏等离子体。幸运的是,我们现在已知如何避免这类不稳定性。本论文研究的是一类增长慢得多的不稳定性,它通常不会破坏等离子体,但会降低等离子体的约束性能。不幸的是,这种被称为“撕裂模”(tearing mode)的不稳定性在磁约束聚变装置中几乎是不可避免的。撕裂模由等离子体电流密度的径向梯度[1]和等离子体压强的径向梯度[2]驱动。
为了理解撕裂模如何降低等离子体约束性能,我们回顾磁约束系统的一个基本特征:嵌套磁通面(或简称为通量面)的存在。在环形几何结构中,常规约束装置的设计使得给定的磁力线在绕装置旋转时呈螺旋状。通常情况下,磁力线在有限次环向绕行后并不会闭合(那些闭合的情况稍后讨论),如果追踪足够长的距离,磁力线最终会在遍历意义上描绘出一个环形磁通面(即磁力线可以任意接近该通量面上的任意一点)。众所周知,在最低阶近似下,带电粒子的运动是以某条磁力线为中心的螺旋轨迹。由于螺旋半径(即拉莫尔半径)通常远小于磁约束装置的典型尺度,粒子基本上被限制在磁通面上。图 1.1 展示了一系列嵌套的环形磁通面。
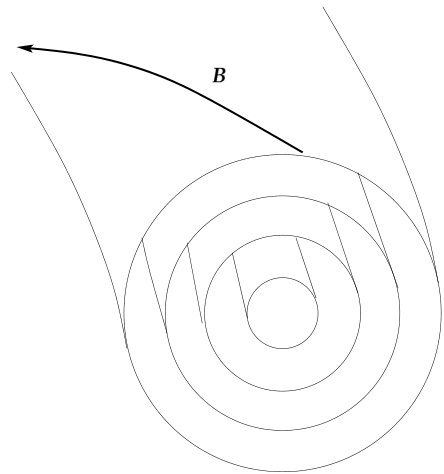
图 1.1:环形截面图,显示一组嵌套的磁通面。引自 Wesson,《托卡马克》[3]。
当我们考虑有限电阻率时,那些磁力线最终闭合的特殊磁通面容易发生撕裂不稳定性,这种不稳定性会“撕裂”并“重联”磁力线,在等离子体内部形成螺旋状的“磁岛链”(见图 1.2)。显然,这类岛链会降低等离子体约束性能,因为热量和粒子能够沿着磁力线从岛链的一侧快速传输到另一侧,这是一种相对较快的过程,而不必缓慢地跨过磁通面扩散[4,5]。此外,当岛链相互重叠时,磁力线将在一个体积内遍历运动,而非局限于一个表面;显然,这是一种不利的约束特性。通常情况下,磁岛的饱和幅度相对较低(即 )[5–8],虽不会完全破坏环形等离子体约束,但确实会使其性能下降。
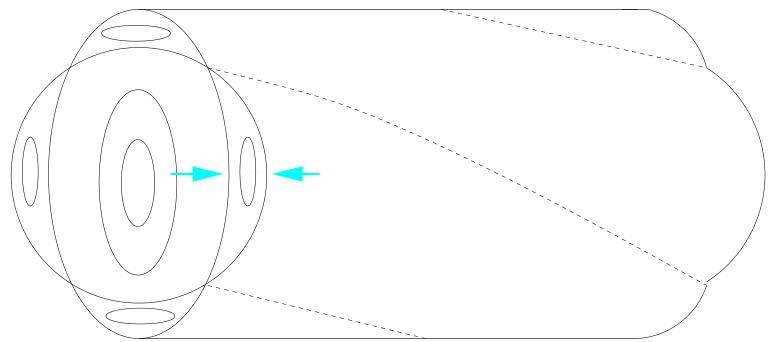
图 1.2:对应磁岛位形的磁通面。箭头表示磁岛的宽度。虚线沿 X 点磁力线。引自 Hazeltine 和 Meiss,《等离子体约束》[10]。
在本论文中,我们将主要研究一种被称为反场箍缩(Reversed Field Pinch,简称 RFP)的磁约束装置。简而言之,RFP 与托卡马克(tokamak)类似,是一种轴对称的环形系统,它通过等离子体环向电流产生的极向磁场 与环向磁场 的组合来约束等离子体 [9]。通过快速浏览典型的磁场分布(见图 1.3),即可看出托卡马克与 RFP 之间的主要区别:在托卡马克中,外部产生的环向磁场远强于极向磁场;而在 RFP 中,环向磁场主要由等离子体内部的极向电流产生,其强度与极向磁场相当。
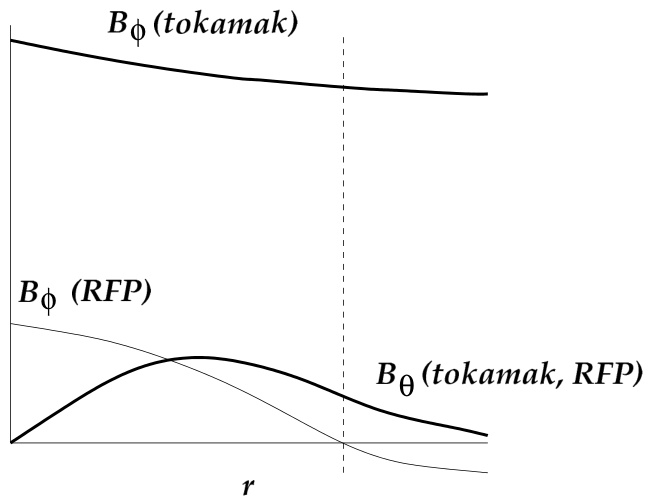
图 1.3:托卡马克(粗线)与 RFP(细线)典型的环向与极向磁场分布,以小半径 为变量绘制。反转面用虚线标出。注意,托卡马克与 RFP 的极向磁场分布大致相同。
此外,正如其名称所示,RFP 在靠近等离子体边缘的反转面处,环向磁场相对于轴上的值会发生令人意外的反转。J.B. Taylor [11,12] 首次指出,这种反转是由等离子体不稳定性自然产生的,是等离子体在有限电阻率驱动下弛豫至最低能量态的结果。这种反转构型对于理想磁流体稳定性是必需的。
人们可能会认为,由于碰撞引起的磁扩散作用,磁场反转只能维持大约电阻扩散时间尺度 的量级,其中 和 分别为等离子体电阻率和小半径。然而事实上,在整个放电过程中,持续存在的低水平模活动(被认为源于撕裂模)通过发电机效应(dynamo action)维持着磁场反转。因此,撕裂模在 RFP 中扮演着双重角色:一方面,RFP 中大部分能量损失可归因于磁岛链重叠所导致的混沌磁场 [13];另一方面,撕裂模活动也负责产生发电机效应,使 RFP 能够维持其磁场反转。
RFP 中的撕裂模通常由于非线性耦合作用 [14] 而锁定相位,形成一种被称为“弹簧模”(slinky mode)[15,16] 的环向局域化磁结构。这种模自然会在面向等离子体的器壁表面产生一个环向局域化的“热点”。通常情况下,弹簧模会与反转面处的等离子体共同旋转,此时热点不会显著降低整体等离子体约束性能 [17]。然而,正如人们所预期的那样,如果弹簧模停止旋转,热点将长时间停留在器壁表面的同一区域,几乎必然导致局部过热、杂质涌入,并最终提前终止放电 [14]。
鉴于撕裂模在 RFP 中扮演的多重角色,理解其动力学行为至关重要。一种研究方法是将问题简化为一组耦合的常微分方程,用于描述各种磁岛链的相位与振幅演化 [18–21]。本论文聚焦于单个磁岛链的演化问题,尤其致力于改进对磁岛链与等离子体之间粘性耦合的处理。正如我们将看到的,正确建模这种耦合至关重要。尽管我们的分析采用 RFP 的参数排序(ordering),但由于托卡马克的参数排序只是 RFP 排序的一个子集,因此我们的演化方程同样可直接应用于托卡马克。
我们将针对两个具体问题定制相位演化方程。首先,我们研究磁岛链在何种条件下会停止旋转。大多数 RFP 等离子体被一层薄的电阻壳包围,该壳起到真空室的作用,而电阻壳外又包围着一层厚的导电壳,用于稳定外部扭曲模(kink modes),否则这些模会迅速破坏等离子体 [22]。已有充分文献表明 [23–25],电阻壳中感应的涡流会对旋转的磁岛链施加制动转矩,使其转速降至极低水平 [26]。当然,仅靠涡流转矩本身无法完全停止旋转,因为当岛链静止时转矩为零。然而,磁岛链可以完全锁定到一个“误差场”(error-field)上,该误差场是平衡磁场中的小幅度非轴对称扰动,可能源于线圈错位、电流馈入设计不当,或导电壳中的绝缘间隙 [27]。因此,撕裂模(以及弹簧模)的锁定很可能是共振误差场与电阻壳中感应涡流共同作用的结果。我们的第一个目标是建立一组方程,描述在存在共振误差场、被厚导电壳包围的薄电阻壳条件下,磁岛链的相位演化。我们的分析将有所简化,仅考虑一个代表性撕裂模的锁定行为,而非构成弹簧模的全部非线性耦合撕裂模集合,但我们希望该处理足够真实,有助于加深对 RFP 中锁定模形成机制的理解。
我们关注的第二个问题涉及主动磁反馈实验。在此类实验中,“误差场”由外部线圈产生,这些线圈被设计用来产生具有特定螺旋度的磁扰动。因此,这种扰动更准确地应称为共振磁扰动(Resonant Magnetic Perturbation,简称 RMP),而非误差场。然而,在本论文中我们将较为宽松地使用术语,有时会将“误差场”与“RMP”互换使用。无论如何,在主动磁反馈实验中,实验者对目标磁岛链施加一个可编程振幅和频率波形的旋转 RMP,通常旨在减小撕裂模的振幅。主动反馈已在多个托卡马克实验中实施 [28–30],取得了不同程度的成功。尽管在反应堆环境中主动磁反馈系统可能并不可行 [31],但它仍是一种直接探测撕裂模物理的有效手段。因此,我们的第二个目标是建立一组常微分方程,描述在外加 RMP 作用下撕裂模磁岛链的振幅与相位演化,可用于解释磁反馈实验数据。
本论文的结构安排如下:第二章介绍撕裂模理论的基本要素,包括由 Furth、Killeen 和 Rosenbluth [32] 首次推导的线性色散关系,以及 Rutherford [6]、Thyagaraja [8] 和 White [7] 研究的撕裂模非线性演化。第三章重新审视 RFP 的基本特性,并回顾 Taylor 理论——如前所述,该理论解释了环向磁场的反转现象。在零 、柱坐标、电阻性磁流体力学(MHD)理论框架下,我们进而推导出一组耦合方程,包括一个偏微分方程(PDE)和若干常微分方程(ODEs),用于自洽地描述 RFP 等离子体中单个撕裂模在与外部误差场及电阻壳中感应涡流相互作用时的相位演化。
第四章关注撕裂模的锁定行为。本章的关键在于通过近似方法,将前述 PDE/ODE 系统转化为一组少量的 ODEs,即我们提出的新近似相位演化方程。与原始的 PDE/ODE 描述相比,这些近似方程在物理诠释上更为清晰,且数值实现也容易得多。此外,与以往推导的相位演化方程不同,它们允许自洽地计算与模共转的等离子体区域的径向宽度——该宽度由粘性决定。利用这些近似相位演化方程,我们对电阻壳对(静态)误差场锁定与解锁阈值的影响进行了全面研究。
尽管第四章推导的近似相位演化方程能够相当准确地预测锁定现象,但其通用性尚不足以模拟磁反馈实验。具体而言,它们不允许外加共振磁扰动的振幅和频率随时间变化,也未考虑磁岛宽度的演化。第五章通过发展一个稍复杂的近似相位演化方程扩展形式,克服了这些不足,使其足以模拟磁反馈实验。随后,我们利用这些方程研究磁岛链对几种简单 RMP 波形的响应,以展示其特性。最后,第六章包含简要的结论与讨论。
第 2 章 撕裂模理论
2.1 什么是撕裂模?
在等离子体物理的理想磁流体力学(MHD)模型中,等离子体被视为无限电导率的流体。众所周知,该模型能够相当准确地描述磁约束聚变装置中的大尺度磁扰动。理想 MHD 的动力学受 MHD 欧姆定律约束:
该方程表明,在无限电导率流体中,以速度 在电场 和磁场 中运动的流体元所感受到的有效(非相对论性)电场为零。由该方程可推出一个重要约束:对于任意闭合回路,若其每一段均随等离子体运动,则穿过该回路的磁通量 是一个守恒量:
因此,磁力线会随等离子体一起运动,或者说“冻结”在等离子体中 [33]。现在我们考虑一个磁通量管的动力学行为,该磁通量管是一个拓扑上呈圆柱形的体积,其侧面由磁力线所界定。根据磁通冻结约束,理想磁流体动力学(MHD)中的等离子体会以保持任意磁通量管“完整性”的方式运动。由于一条磁力线可被视为无限细的磁通量管,因此理想 MHD 中的等离子体运动也保持磁力线的完整性。也就是说,理想 MHD 禁止磁力线拓扑结构的任何改变,磁力线不能断裂或重新连接。事实上,这对磁场的动力学施加了非常严格的限制。
现在我们在问题中引入有限的电阻率 。理想 MHD 的欧姆定律被非理想欧姆定律所取代:
将其与法拉第定律和安培定律结合,可得:
方程右侧第一项描述了磁场随等离子体流动的常规对流效应,第二项则代表磁场在等离子体中的电阻扩散效应。因此,等离子体与磁场不再冻结在一起,磁力线的拓扑结构可以自由改变。因此,尽管电阻率通常起到抑制扰动的作用,但在 MHD 框架下,电阻率也可能扮演一种失稳机制的角色。由于等离子体摆脱了磁通冻结约束,磁力线可以“撕裂”并“重新连接”,形成具有更低势能的新构型。这构成了撕裂模不稳定性的基本机制。
人们可能会认为,由电阻率驱动的模会以磁场在整个等离子体中扩散的时间尺度增长:
其中 是典型的平衡尺度长度。通常而言,以该时间尺度增长的模增长得过于缓慢,因而并不值得关注。然而,正如我们将看到的那样,等离子体跨磁场的扩散发生在远小于平衡尺度的长度上,却仍能释放大量磁能。因此,该模的增长速度远快于缓慢的全局电阻扩散时间尺度。
2.2 平板几何
尽管本论文的工作聚焦于柱几何,但撕裂模的基本特性在平板几何下或许能得到最清晰的说明,我们现在就来考察这种情形。考虑一个在 和 方向上均匀的无限大等离子体,其中包含一个剪切的平衡磁场:
其中 。该构型如图 2.1 所示。
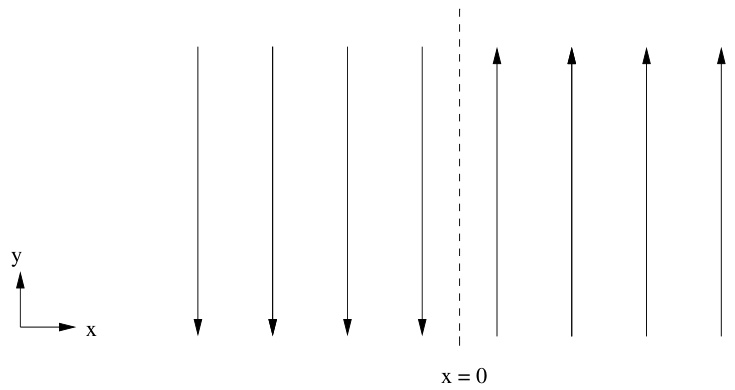
图 2.1:适用于撕裂模分析的简单剪切平衡磁场
磁场在原点处改变符号,从而在 处形成一个沿 方向的电流片。如果界面 两侧方向相反的磁力线能够以某种方式相遇并相互湮灭(或抵消),则系统的磁能 将会降低,这在能量上是有利的。然而,在理想 MHD 中,这类运动是被禁止的,因为根据磁通冻结约束, 平面内任意等离子体面元所穿过的磁通量必须保持不变。事实上,可以证明该构型确实是理想 MHD 稳定的 [34]。当然,当我们引入有限电阻率时,磁通冻结约束被放松,来自界面一侧的磁力线便可以通过等离子体扩散到另一侧并与之湮灭。事实上,正如我们将看到的,平板降低其磁能的具体方式并非如此简单:电阻率允许磁场通过一种波动形式的扰动 在界面处“断裂”并“重新连接”,从而通过形成“磁岛”来降低磁能。
现在,我们通过考虑如下形式的平衡磁场来推广这一情形:
其中强的 分量近似均匀,但 分量依赖于 ,因此当我们沿 方向移动时, 会发生旋转。此外,我们选择 和 轴,使得当 时 ;当然,我们也可以将坐标轴取向为在任意 处 。我们在图 2.2 中展示了该平衡磁场。注意,如果我们只观察 ,我们会得到与图 2.1 相同的图像。因此,由方程 (2.6) 所描述的平衡态代表了一类更普遍的平衡态。
现在,由于该平衡态在时间上是定常的,并且在 和 方向上是均匀的,
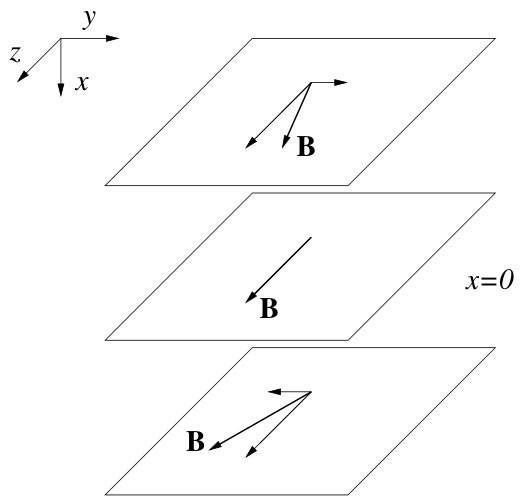
图 2.2:广义剪切磁场 。图中展示了磁场 及其分量 、。注意,我们已将 和 轴取向为使得 。
因此可以合理地假设扰动具有如下形式:
其中 。电阻撕裂不稳定性满足
在所谓的“共振面” 处成立,撕裂模在此处重联磁力线。对于方程 (2.6) 所描述的简单平衡态,共振条件 (2.9) 在 处满足,这正如我们所预期的。而对于由方程 (2.7) 描述的更一般的平衡态,由于在无限等离子体平板中允许所有 值,条件 (2.9) 可在任意 值处满足。因此,任意 值都可能是撕裂不稳定性的发生位置。目前,我们集中研究如下形式的扰动:
这里为简化记号,我们将 。在此情况下,对于由方程 (2.7) 描述的平衡态,条件 (2.9) 仅在 处满足。
在继续之前,请注意方程 (2.9) 的物理意义:它表明在撕裂模重联磁通量的表面上,波矢平行于磁场的分量 为零。具有显著 分量的扰动需要消耗能量来弯曲磁力线。因此,若 ,则扰动在弯曲磁力线方面消耗的能量极少,从而有充足的能量用于流体运动,进而促进其增长 [10]。
2.3 线性分析
现在准备工作已经就绪,我们希望通过线性分析获得撕裂模的色散关系。该问题最早由 Furth、Killeen 和 Rosenbluth 在一篇经典论文中成功处理 [32]。我们再次考虑具有方程 (2.7) 所述平衡磁场的无限等离子体平板。同时,我们采用电阻形式的欧姆定律(方程 (2.3)),并假设等离子体流动是不可压缩的,且无零阶分量。于是,电阻磁流体力学(resistive-MHD)的线性化方程组具有如下形式:
其中, 是平衡态等离子体密度,、 和 分别表示扰动的磁场、等离子体速度和压强。注意,
第一个方程就是方程 (2.4)。第二个方程是磁流体力学的力平衡方程。最后一个方程当然是不可压缩条件,它源于平衡磁场中强的 分量。
假设扰动具有形式 (2.10),则方程 (2.11) 的 分量和方程 (2.12) 的旋度的 分量变为
其中我们使用了式 (2.13–2.14),以及由扰动形式 (2.10) 和平衡态 (2.7) 所导出的 。此外,此处的撇号表示对 的导数,即 。由式 (2.15) 可知,在无电阻情况下,只要 ,则 也必须为零,以避免等离子体速度发散。有限的电阻率 放宽了这一约束,使得磁场可以通过有限的 在 界面处发生“撕裂”和“重联”。
撕裂模的所有动力学行为都包含在耦合方程组 (2.15) 和 (2.16) 中。通过采用渐近匹配方法 [35],可以极大地简化其求解过程。具体而言,我们将等离子体划分为两个区域:一个是以 为中心、宽度很窄的“内区”(或称内层),在此区域内电阻率和惯性效应都很重要;另一个是“外区”,在此区域内理想磁流体力学(MHD)成立,因此可以忽略电阻率(并且,如我们稍后将看到的,也可以忽略惯性效应)。在每个区域内,我们可以分别求解简化后的方程 (2.15–2.16),然后在中间的匹配区域将内区解和外区解进行匹配。也就是说,我们要求内区解和外区解在内区与外区重叠、且两者均有效的区域内具有相同的 函数依赖关系。通过这种匹配,我们将能够得到撕裂模的色散关系。
现在我们对式 (2.15) 和 (2.16) 进行无量纲化。定义典型的磁场强度 和典型的长度尺度 ,引入阿尔芬时间尺度
其中 是阿尔芬速度,以及电阻扩散时间尺度(见式 (2.5))
这两个时间尺度之比(通常非常大)即为伦德奎斯特数(Lundquist number):
现在我们引入如下无量纲变量:,,,,,,以及 。于是,式 (2.15) 和 (2.16) 可改写为无量纲形式:
与式 (2.15) 和 (2.16) 对比可知,式 (2.20) 右侧(RHS)的项代表等离子体的电阻率效应,而式 (2.21) 左侧(LHS)的项代表等离子体的惯性效应。
我们假设撕裂不稳定性以一个混合时间尺度增长,该时间尺度远小于 但远大于 ,即满足
因此,在等离子体的大部分区域中,我们可以忽略式 (2.20) 的右侧项和式 (2.21) 的左侧项,这分别等价于忽略等离子体的电阻率和惯性效应。在此情况下,式 (2.20–2.21) 简化为
第一个方程只是磁通冻结约束,第二个是线性化的静态力平衡方程 。这两个方程(2.23–2.24)共同构成了理想磁流体力学(MHD)方程,并且如前所述,在等离子体主体区域内均成立。然而,在狭窄的“内区”中这些方程失效,这一点可由以下事实证明:当 时(从而 ),等离子体速度 趋向无穷大。
这类奇异性可通过在内区引入惯性和电阻效应加以解决。在此区域内, 且 ,因此方程(2.20–2.21)可简化为边界层方程:
其中我们重新定义了变量 、 和 ,使得 、 以及 。这些定义在本节其余部分均适用。此处,
为磁流体时间尺度,具有简单的物理意义 [34]。考虑一个波数为 、沿 方向传播的剪切阿尔芬波,并假设方程(2.7)中的 分量非常强。在此情况下,该波的频率为
其中在最后一个等号中,我们近似取 且 (注意 和 分别为典型的长度尺度和磁场强度)。由方程(2.17)、(2.27)、(2.28)以及 的定义可知,。
在继续之前,我们注意到可以通过联立方程(2.25–2.26)得到边界层宽度的估计值 [34]:
平衡上述方程左边的两项,可得边界层的特征宽度为
我们很快会看到,在大多数情况下,撕裂模的增长率满足 (见方程(2.59)),因此归一化的边界层宽度变为
正如预期的那样,由于 ,故 ,并且随着电阻率减小(即 增大), 会变得更小。
现在我们可以概述我们的求解策略。设想从较大的 处出发,对“外区”方程(2.24)进行积分(施加适当的边界条件,例如 ),一直积分到边界层边缘 ,从而得到区域 中的 。类似地,我们也可以通过对 为较大负值处的方程(2.24)进行积分(同样施加适当的边界条件),积分至边界层左侧 ,从而得到区域 中的 。根据麦克斯韦方程,()在边界层两侧必须连续。由于我们处理的是线性问题,可以自由地将两个解乘以适当的系数,以满足这一连续性条件。然而,在 处的电流片通常要求 在边界层两侧不连续,这意味着根据方程(2.13), 也存在不连续性。因此,我们可以用一个实数来表征理想 MHD 解:
这被称为撕裂稳定性指数(tearing stability index),用于衡量在 处流动的扰动电流片。事实上, 与撕裂模所能释放的“势”磁能成正比 [41]。考虑进入非理想层的净电磁能量通量是有启发性的:
其中
是坡印廷矢量的“径向”分量。简单的计算表明,
其中 是该模的增长率。因此,若要该模自发增长()并从平衡态中释放磁能(),我们需要 。
最后需要注意的是, 仅由外区方程 (2.24) 决定,且只依赖于等离子体平衡态、波数 以及无穷远处的边界条件。例如,对于如下简单的平衡磁场
其中 为常数,我们可以直接求解外区方程 (2.24),得到 [34]
此处应用了边界条件:当 时,。
我们稍后将对式 (2.37) 进行更多讨论,但目前我们继续概述求解方法。在未研究内区的情况下,我们已得到了驱动不稳定性的自由能源项 的表达式,但我们尚不清楚它如何与增长率 相关联。正如预期的那样,为了获得这一最终环节,我们必须求助于依赖惯性的层内方程 (2.25–2.26),因此也依赖于 。这些层内方程具有一个平凡解(,,其中 与 无关)和一个非平凡解,后者满足 且 。撕裂模对应于后一种解。
由于包含了电阻率,层内方程 (2.25–2.26) 构成了一个四阶系统,包含四个待定系数。然而需要注意的是,我们的层内解在前述匹配区域内必须与外区解具有相同的 函数依赖关系。通过将(Frobenius)幂级数解代入方程 (2.23) 和 (2.24),可以得到外区解在 时的渐近行为:
其中 和 是二阶系统 (2.23–2.24) 的两个任意常数。内区解在远离原点处()必须表现出相同的 依赖关系,因此我们可以写出内区解的渐近行为:
参数 和 代表与四阶系统 (2.25–2.26) 相关的四个未定常数中的两个。其余两个常数分别对应于平凡解和指数增长解,因此可以舍弃。于是,我们现在可以通过求解边界层方程以确定系数 的具体形式,然后令
该式由方程 (2.32) 和 (2.40) 推出。
接下来,我们尝试找出 的显式表达式。按照 Coppi 等人 [36] 的方法,我们对四阶边界层方程进行傅里叶变换,将其化为一个二阶方程,所用的变换对为
对 也定义了类似的变换对。边界层方程 (2.25–2.26) 经变换并合并后可得
其中
注意,此处所用的变换对与“通常”的傅里叶变换(即 )不同:我们在指数函数的自变量中引入了一个便于处理的“拉伸”因子 。因此,方程 (2.43) 实际上给出的是 而非 的“通常”变换。关键在于,尽管 在区域 内高度局域化,但 则局域于更大的区域 ,即 ,这里我们使用了方程 (2.31)。因此,我们实际上已将非理想层的边缘“拉伸”至 。
我们现在关注的是匹配区域中 的行为,该区域远离非理想层的边缘。根据之前的讨论,在方程 (2.43) 的“拉伸”坐标下,该匹配区域对应于 。再考虑到傅里叶变换将大 行为映射为小 行为,我们实际上需要的是方程 (2.45) 在小 下的渐近解,其形式为
其中 和 是该二阶方程的两个未定系数。此外,我们假设 。由于 是奇函数,因此 也是奇函数,这意味着当 时,。
对该表达式进行逆变换 [37, 38] 后,可得非理想磁流体力学(MHD)层边缘处 的渐近行为为:
此处仍假设 。注意,由于我们工作在非理想层的边缘,常数项的反射(即当 时 )并不必然导致 不连续。将方程 (2.40–2.41) 与方程 (2.48) 进行比较,可得
因此,我们发现匹配参数 由傅里叶变换后内解在小 极限下的两个最低阶系数之比所决定。下一步便是确定该比值。
我们将寻找一种不稳定的撕裂模,其特征为 。为方便起见,假设
这种排序被称为恒定-近似(因为它意味着在层内近似为常数),其合理性将在后文予以说明。在极限下,方程(2.45)简化为
该方程在极限下具有良好行为的解可写作,其中是一个标准的抛物柱面函数。 在极限
下,我们可以利用的小宗量展开式,将方程(2.51)的解写成如下形式:
其中是一个待定常数。
在极限
下方程(2.45)简化为
该方程的解为
其中和为任意常数。在满足方程(2.52)的范围内,将方程(2.53)与(2.56)进行匹配,即可得到方程(2.45)在范围内的解:
因此,我们最终得到了比值(见方程(2.47)),并可利用方程(2.49)将匹配参数表示为增长率的函数:
将上述的表达式与渐近匹配条件(2.42)相结合,即可得到撕裂模色散关系:
其中用到了 和 的定义。该色散关系仅在 时成立。当 时,上述推导可稍作修改,表明此时该模是纯衰减的。因此,根据上述色散关系,只要 ,撕裂模就是不稳定的,并以混合时间尺度 增长。
注意,在推导方程 (2.59) 时,我们使用了“恒定- 近似”(2.50)。由方程 (2.40) 和 (2.42) 可知,只要满足
在电流片内确实近似为常数;或者利用方程 (2.31),即 ,也就是说,只要撕裂模没有变得过于不稳定。通过方程 (2.42)、(2.50) 和 (2.58),可以得到一个稍严格的恒定- 近似适用条件:
为了更清楚地理解恒定- 近似 (2.50) 的来源,我们注意到:当撕裂模的增长时间尺度远大于磁通量在非理想层内扩散的时间尺度时,该近似成立。在这种情况下,我们预期 (即 )的任何非均匀性都会通过电阻扩散在层内被抹平,从而验证了恒定- 近似。这一条件可表示为
其中
是磁通量穿过宽度为 的非理想层的扩散时间尺度 [参见方程 (2.18)]。由方程 (2.30) 可知,方程 (2.62) 变为
再利用 的定义 [方程 (2.46)],即可回到我们之前得到的条件,即方程 (2.50)。
2.4 磁岛
如前所述,撕裂不稳定性会改变磁场的拓扑结构。下面我们更清晰地描述这一现象。我们考虑简单的平衡态,如方程 (2.6) 所示。按照惯例,我们利用磁场无散度且与 坐标无关的性质,将其表示为磁通函数 的形式:
其中 和 分别代表典型的磁场强度和典型长度尺度。根据定义,磁通函数 满足
因此 与 为常数的曲面相切。
我们可以在界面 附近将磁通函数表示为
其中 对应于平衡磁场 (见式 (2.6)),而 对应于撕裂模扰动磁场 。此处 ,。注意,在写出式 (2.67) 时,我们采用了常 近似,这意味着在 附近有 ,从而 。现在,考虑到平衡磁场关于 是奇函数,并假设 的相位使其在 方向按 变化(见式 (2.10)),则式 (2.65) 和 (2.67) 表明在界面附近有
此处,与前一节相同,,而 是一个与扰动磁场 幅度成正比的常数。我们引入归一化的磁通函数 、一个“角”坐标 ,以及一个“径向”坐标 ,其中
由此可得,式 (2.68) 可重写为
图 2.3 绘出了在 空间中 的等值线,这些等值线即为磁通面。图 2.3 可与图 2.1 中的初始磁场位形进行比较。从图 2.3 可见,在位于 处的磁分界线(separatrix)内部,磁场发生撕裂并重联,形成以“O 点”为中心的磁岛,这些 O 点位于 和 处,其中
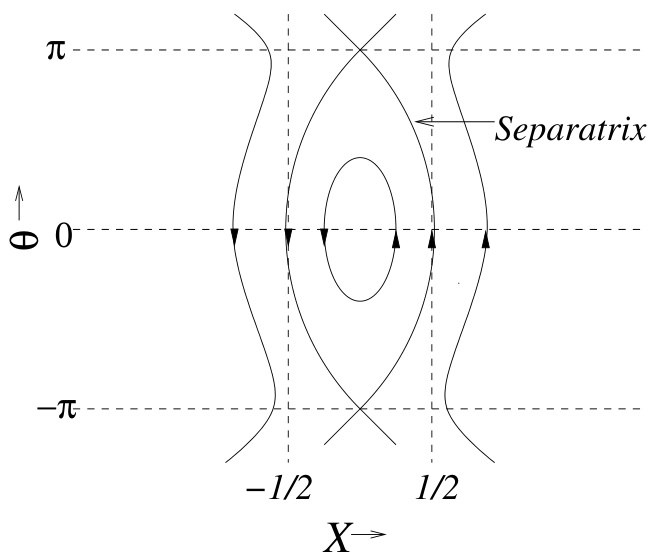
图 2.3:与电阻性撕裂不稳定性相关的磁力线位形。该图案在 方向上以周期 重复。
为整数。在分界线之外,存在位于 和 处的“X 点”,此处磁力线拓扑结构保持不变。注意,由分界线所形成的最大磁岛在 方向的宽度即为 (见式 (2.69)),因此它正比于界面处扰动的“径向”磁场 的平方根。
2.5 撕裂模的非线性理论
如前所述,线性理论预测撕裂模在一种混合的流体-电阻时间尺度上呈指数增长。当磁岛宽度超过线性撕裂层宽度(即 )时,Rutherford [6] 提出,非线性涡流所产生的力将取代惯性,成为抑制模增长的主要机制。因此,增长速度显著减慢,磁岛宽度 在极慢的电阻时间尺度 (见式 (2.18))上按如下关系增长:
其中 ,而撕裂稳定性指数 由式 (2.32) 定义。
为推导这一结果,我们在平板几何下工作,采用熟悉的平衡磁场 (2.7),并再次将其用磁通函数 表示为:
由于存在强而均匀的 分量,我们可以假设速度场 是不可压缩的,因此 可用流函数 表示为:
与线性情形类似,我们结合法拉第定律和欧姆定律,将其用磁通函数表示为
以磁通函数表示的安培定律为
最后,我们需要等离子体的运动方程:
该方程可改写为以涡量 表示的形式,即
我们现在做出一个基本假设:我们关注的是模增长得非常缓慢的情形,以至于惯性项可以忽略。在此情况下,式 (2.77) 意味着 是一个磁通函数(参见式 (2.66)):
接下来,我们将磁通函数展开为
其中
注意到在 附近有 ,因此 。此外,尽管式 (2.79) 和 (2.80) 的记号中未显含 , 实际上仍具有一定的 依赖性。然而,与前一节类似,我们假设常磁通近似适用于 。也就是说,在我们所关注的区域内——该区域是一个“径向”层,其尺度远大于线性层宽度 (见式 (2.31))和磁岛宽度 (见式 (2.69))——我们假设 近似为常数。根据式 (2.60),只要满足
这一假设就成立,其中
是通常的撕裂模稳定性指标。将式 (2.79) 代入式 (2.74),我们得到
注意,第二项代表非线性贡献 ,这里用速度流函数 表示。乍看之下,似乎需要计算 才能继续,但 Rutherford 注意到,通过对磁通面进行平均,可以完全消去该项。具体而言,在将式 (2.83) 除以 后,我们在恒定 下对 进行平均,得到
其中
表示 在磁通面(flux surface)上的平均值。注意,对于位于分界线(separatrix)内部的 值(此时磁力线是闭合的),该磁通面平均的定义必须加以修正,使得式 (2.85) 中的积分限依赖于 。此外,尽管我们已消除了式 (2.83) 中的非线性项,但代价是磁通面平均本身具有高度非线性(即我们积分所用的等 面是由式 (2.79) 中所有谐波共同决定的曲面)。
现在,将式 (2.75) 在我们感兴趣的区域内积分,两边同乘以 以提取第 阶谐波分量,并进行磁通面平均,同时考虑到 的梯度不连续性由 描述,最终得到:
在第二个等号中,我们通过将式 (2.84)(其中积分变量已换为 )代入 ,从而“闭合”了方程。Rutherford 认为,在基频模线性不稳定()而所有其他高次谐波相对强稳定()的情况下,存在一种解,其中基频模占主导地位()。在此情形下,我们可以回到式 (2.86),显式计算积分,从而得到磁岛演化方程:
其中 [40]。可以很容易地验证,式 (2.87) 与式 (2.71) 确实等价。
正如人们所预期的那样,磁岛并不会无限增长,最终会达到饱和。White 等人 [7] 对此饱和过程进行了启发式研究,而 Thyagaraja [8] 则通过更严格的方法——将内区与外区解在更高阶上进行匹配(即在式 (2.38) 中继续展开至最低阶项之后的高阶项),并利用磁通面平均——得到了如下结果:
其中 是一个与平衡电流梯度相关的常数,且如前所述,。注意,式 (2.88) 预言在某个宽度 处(由下式定义):
磁岛将达到饱和,但并没有特别的理由说明 一定很小。然而需要注意的是,式 (2.89) 仅在 的极限下才准确。尽管如此,关键点在于:即使理想磁流体力学(ideal MHD)仅在很小的区域 内失效,平衡磁场的变化却发生在与等离子体尺度相当的区域内!
2.6 柱坐标几何
到目前为止,为了清晰起见,我们一直局限于平板几何(slab geometry),但大多数感兴趣的聚变装置采用环形几何(toroidal geometry)。事实上,我们将限于大纵横比、零 (即 )的等离子体平衡态,其未受扰动的磁通面在极向截面中近似为同心圆。这种平衡态可很好地近似为周期性圆柱,因此我们采用标准的柱坐标 。由于该圆柱用于近似环面,我们必然假设等离子体在 方向具有周期性,周期长度为 ,其中 是模拟的等离子体主半径。为方便起见,我们定义一个模拟的环向角 。我们关注如下形式的平衡磁场:
一般而言,磁场会缠绕(cylindrical)磁通面,形成螺旋线。基于式 (2.90),我们假设扰动具有如下形式:
其中 和 为任意整数。
在环形或柱形几何中,一个重要的物理量是安全因子 ,它用于度量磁场绕柱体缠绕时的平均螺距。对于本论文所考虑的简单平衡态(其磁通面近似为圆形,且平衡磁场具有式 (2.90) 的形式),安全因子 具有如下特别简单的表达式:
若考虑一个沿磁场方向的线元 (即满足 ),则可简单证明该线元满足
这清楚地表明了 作为磁力线螺距度量的作用。
回顾平板几何的情形,撕裂模要在等离子体中某表面 上形成,该表面必须满足共振条件 。在柱形几何中,对应的共振面具有半径 ,若假设扰动具有式 (2.91) 的形式,则共振条件可简洁地用安全因子表示为:
因此,为了使扰动的波矢垂直于平衡磁场,磁场的螺距()必须等于扰动的螺距(),这与我们的预期一致。结果是在“有理面” 上,磁力线在完成 圈环向和 圈极向绕行后闭合于自身。通常 是一个单调函数,而由于 和 是任意整数,可见式 (2.94) 将在无穷多个有理面上成立(尽管这些有理面仍是特殊的,因为有理数集合的测度为零)。然而在实际中,只有那些“低阶”有理数(即 和 较小,对应扰动具有足够长波长)才会对应不稳定的撕裂模。
为理解这一点,我们回顾平板几何中的结果 (2.37),此处重写如下:
作为 的函数, 是一个单调递减函数:当 较小时为正,当 较大时为负。由于撕裂模仅在 时不稳定,可见只有长波长扰动才值得关注。从物理直觉上看,这是合理的。回想一下,撕裂模通过在共振面上重联磁场来降低磁构型的磁能,从而形成磁岛链。从图 2.3 可以清楚看出,重联必然涉及磁力线的弯曲,而弯曲所需的能量随波长减小而增加。因此,当弯曲磁力线所需的能量足够大时,重联就不再具有能量优势,撕裂模也就变得稳定。
当然,当我们转向柱形几何时,撕裂模的图像需要稍作修正。具体而言,撕裂模表现为具有 螺旋对称性的磁通管(参见图 1.2)。当我们对柱体取横截面时,即可恢复熟悉的磁岛图像。除了图像上的差异外,柱形几何带来的另一个主要变化体现在 的形式上。需要注意的是,尽管由窄层方程决定的内解与几何无关,但外解(以及完全由外解决定的 )则强烈依赖于几何形状。柱形几何下线性撕裂模色散关系及非线性 Rutherford 磁岛演化的推导可见文献 [10]、[41] 和 [3]。所得结果的形式基本保持不变。
第 3 章 RFP 中的撕裂模动力学
3.1 概述
本文所研究的基本问题是:在反场箍缩(RFP)装置中,受误差场和电阻壁作用的撕裂模的动力学行为。我们假设撕裂模磁岛链足够宽,使其非线性演化,并将该磁岛链视为被困在一种唯象的(不可压缩)粘性流体中的障碍物 [42]。该磁岛链将响应电磁力矩和粘性力矩的作用,从而构成一个耦合的 MHD/流体力学问题。我们利用 MHD 方程计算作用在有理面上等离子体的电磁 力矩,并利用流体方程计算作用在磁岛链上的粘性力矩。注意,电磁电流与磁岛链的相互作用有两种方式:若电流与磁岛链同相位,则会改变其宽度演化;若电流与磁岛链存在 90 度相位差(正交相位),则会产生 力矩。
本章首先介绍反场箍缩(RFP)的一些基本性质,这是本论文关注的主要聚变装置。在讨论了泰勒(Taylor)的弛豫理论之后,我们利用磁流体动力学(MHD)方程求解RFP的撕裂模本征函数,并利用这些本征函数计算作用在磁岛链上的电磁力矩。最后,我们引入等离子体所满足的流体运动方程。到本章结束时,我们将得到一套完整的相位演化方程,用于描述撕裂模的动力学行为。这些方程的“求解”将是下一章的主题。
3.2 反场箍缩(RFP)简介
反场箍缩(Reversed Field Pinch,简称RFP)是一种轴对称的环形聚变装置,在许多方面与其广为人知的“近亲”托卡马克(tokamak)[9,14]相似。具体而言,它通过极向磁场 和环向磁场 的组合来约束等离子体。此外,与(常规)托卡马克一样,RFP通常也具有较小的反比纵横比 。然而,与托卡马克中 不同,RFP中的环向磁场主要由等离子体中的极向电流产生,其强度与极向磁场相当。因此,安全因子 (见式(2.92))远小于1(而在托卡马克中 ),且 ,表明RFP比托卡马克(其中 )能更高效地约束等离子体。作为一种磁约束聚变概念,RFP相对于托卡马克具有若干潜在优势[14]。首先,RFP线圈处的磁场强度相对较低,使得有可能使用铜线圈而非(技术上更具挑战性的)超导线圈来建造反应堆。其次,与托卡马克中必须限制等离子体电流以稳定外扭曲模不同,RFP中的等离子体电流原则上可以增大到足以实现欧姆点火(ohmic ignition),从而无需辅助加热系统。
RFP的主要代价在于其构型远比托卡马克不稳定。事实上,为了稳定外扭曲模(否则会迅速破坏等离子体[22]),常规RFP等离子体必须被一个厚导电壳包围,该壳的电阻穿透时间远长于放电持续时间。即便有导电壳存在,RFP等离子体对内扭曲模仍然不稳定。图3.1比较了托卡马克和RFP的安全因子 剖面;显然,RFP比托卡马克具有多得多的共振面(即 的位置)。在导电壳存在的情况下,主导的MHD模是多个 的撕裂模,它们在等离子体芯部共振,并具有范围广泛的环向模数 ,其特征为 [27]。关于RFP的更多细节,包括力平衡与稳定性等问题,读者可参考文献[9]、[44]和[39]。
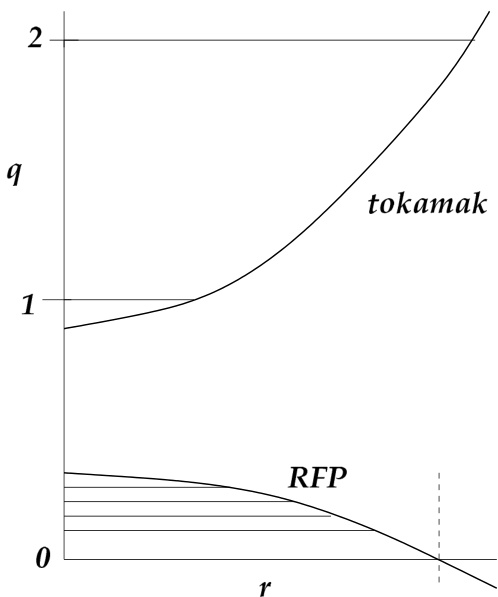
图3.1:托卡马克与RFP中 剖面及可能共振面的示意图。在托卡马克中,主要共振面 对应 且 ;而在RFP中,存在许多 且 的共振面。虚线表示反转面。引自Biskamp,《非线性磁流体动力学》[39]。
3.3 泰勒弛豫理论
RFP最引人注目的特性之一是其边缘区域环向磁场相对于轴上值的意外反转。正如第一章所述,J.B. Taylor [11,12] 首次指出,这种反转是由等离子体不稳定性自然产生的,是系统在有限电阻驱动下弛豫至最低能量态的结果。在处理该问题时,Taylor基于一个非常简单的物理图像:他考虑一个柔性、理想导电、载流的线圈环浸没在粘性流体中,并询问该线圈在与其自身磁场达到平衡时最终会采取何种构型。初始时,线圈会剧烈摆动,将能量传递给流体,直到磁能 (其中 为线圈的自感)在总磁通 保持不变(因线圈被假定为理想导体)的约束下达到最小。
由于我们可以粗略地将等离子体视为无穷多个相互链接的柔性导体,因此可以预期类似的情形:即再次在适当约束下最小化磁能
(我们假设等离子体对能量的贡献可忽略)。当然,问题的关键在于确定这些约束条件。让我们首先考虑一个被刚性理想导电壳包围的等离子体。对于理想导电等离子体,回忆其满足
该式由法拉第定律和欧姆定律导出。如前所述,上式要求随等离子体一起运动的任意磁通环的磁通量保持不变。因此,现在我们已经熟悉:在最小化 时对 进行变分,不允许系统拓扑结构发生任何改变(即不允许磁力线撕裂或合并)。注意,式(3.2)意味着
其中 为等离子体位移,满足 ,且我们假设背景是静态的。因此,我们可以对等离子体位移变分以最小化 :
其中积分区域为等离子体体积,最后一步通过分部积分完成(表面项为零,因为假设等离子体被理想导电壳包围)。由于 是任意的,弛豫后的等离子体平衡态满足
且
其中后一关系由 推出。此外,如常, 用于标记磁通面。方程 (3.5) 描述了一种无力平衡态(即电流与磁场平行)且压强为零()的情形。进一步地,正如我们即将看到的,磁通函数 并非自由参数,而是由等离子体的初始状态所决定。
当等离子体为理想导体时,我们已得到了合适的平衡态。然而,在“真实”的等离子体中,总会存在微小的电阻率。让我们尝试将无限电导率约束改写为一种形式,使得推广到有限电阻率的情形(相对)直接明了。为此,我们必须引入所谓的“磁螺旋度”:
其中积分区域为任意磁通面所包围的体积。为了理解这一物理量的含义,考虑两条闭合且相互缠绕、横截面无穷小的磁通管,如图 3.2 所示 [43]。由于磁通管按定义构成磁通面,我们可以对每条磁通管应用方程 (3.7)。
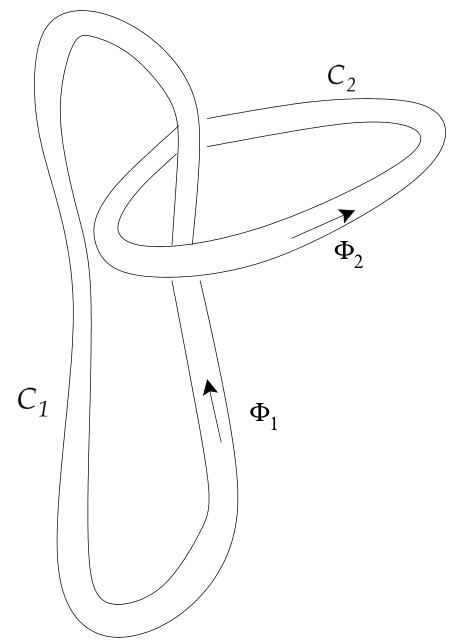
图 3.2:两条相互缠绕的磁通管。箭头表示磁场方向。
考虑
其中 是由闭合曲线 所描述的磁通管的体积。在此体积内,我们可以将 重写为 ,其中 是沿磁力线方向的线元, 是磁通管的无穷小横截面积, 是磁通管中的(恒定)磁通量。因此,
其中 是由曲线 张成的曲面, 是对应于 的磁通管所包围的磁通量。类似地,
更一般地,若两磁通管相互缠绕 次,则
其中符号取决于两管的相对取向是右手系还是左手系(图中每条磁通管相对于另一条均为右手取向,因此螺旋度为正)。关键在于, 直接与拓扑量 相关。
现在回顾一下,在理想导电流体中,磁力线的拓扑结构不能改变,即若一条闭合磁力线绕另一条 圈,则在等离子体演化过程中,这两条磁力线必须始终保持 次缠绕。因此可以预期,在理想导电流体中, 是一个运动常数,事实确实如此。具体而言,
或者,通过分部积分,
注意,方程 (3.2) 意味着
其中 是任意标量函数。将式 (3.14) 代入式 (3.13),并再次使用分部积分法,可得结果
因此,式 (3.7) 表示无穷多个运动常数。具体而言,当场线闭合时,每条场线对应一个不变量(此时式 (3.7) 中的体积对应于包围该场线的无穷小磁通管);而当场产生磁通面时,每个磁通面对应一个不变量。回到本节开头所描述的类比,我们可以看到,我们的直观图像已从单一回路带一个约束()的情形,转变为无穷多个“回路”(对应于场线)以及无穷多个约束(对应于式 (3.7) 中的不变量)的情形。
Taylor 指出,若在式 (3.7) 所体现的无穷多个约束条件下最小化 (详见文献 [44]),实际上仍会得到我们之前熟悉的平衡条件 (3.5–3.6)。因此,使用无限电导率约束 (3.2) 或使用无穷多个积分约束 (3.7) 来最小化 是等价的,这正如我们所预期的那样。如前所述, 并非任意函数,原则上可通过求解 来确定 和 (假设 为任意函数)。由此得到的 和 可用于计算 。由于 是一个运动常数,故有 ,其中 是初始状态给定的螺旋度。
最后,我们对上述关系进行反演,得到 。因此,由 所决定的最终平衡态与初始状态密切相关。
如前所述,在真实等离子体中,无穷多个约束 (3.7) 过于严格。毕竟,即使允许极小的电阻率,“磁通冻结”定理的严格性也会被削弱,等离子体便可自由改变其拓扑结构。因此,我们不能再假设每个磁通面上都有 ,因为场线持续的撕裂与合并会破坏大多数磁通面的身份。然而,等离子体边界这一磁通面在整个弛豫过程中仍将保持其身份,因为它被一个刚性且理想导电的外壳所包围。事实上,若定义
其中 为等离子体的总体积,则在非零电阻率情形下,
因此在小电阻率极限下, 是一个近似的运动常数(等离子体弛豫的时间尺度远小于电阻扩散的时间尺度)。于是 Taylor 猜测,我们应在单一约束 下最小化 。引入拉格朗日乘子 ,我们最小化
关于矢势 ,从而得到最低能量态满足
如前所述,有关最小化的细节请参见文献 [44]。注意,该平衡态仍是无力场(force-free),但现在由单一常数 而非函数 所表征。此外,对于类似的初始条件,由式 (3.19) 所描述的能量态将低于由式 (3.5) 描述的能量态,因为除一个约束外,无穷多个约束 (3.7) 均已被放松。
通常用箍缩参数 来表征 RFP(反场箍缩)平衡态,该参数用于度量环向电流,定义为
其中 是环向磁场的体积平均值, 是等离子体的小半径, 是等离子体中的总环向磁通(由于周围存在理想导电壳,该磁通守恒), 是等离子体的总环向电流。考虑大环径比的环(即近似为直圆柱),并限定 足够小(确切地说 ),则式 (3.19) 的最低能量解为轴对称贝塞尔函数模型:
其中轴上的环向磁场 通过下式与环向磁通 相关联:
由式(3.20–3.22)可知,常数 仅由箍缩参数决定,关系如下:
因此,贝塞尔函数模型具有一个显著特性:当给定电流 和磁通 (从而确定 )时,该模型无需任何拟合参数即可预测磁场分布及其幅值。注意,当 足够大时(即 ,或 ),该模型预测会出现磁场反转。尽管在大多数实验中 相对较高且 并非常数 [9],贝塞尔函数模型与实验结果的对比仍然相当好。关于后一点,实践中发现 可以很好地用 模型描述 [45]:
其中 是一个正的常数,满足 ,而 是另一个正的常数,通过拟合实测剖面确定。注意,当 时, 为常数;但当 为有限值(通常情况如此)时, 在等离子体边界处降为零。其原因是边界等离子体足够冷且电阻率较高,无法维持与泰勒态(Taylor state)相关的强平衡电流 [14]。因此,观测到的位形并非严格的最小能量态。
由于等离子体芯部电阻率较低,电流在那里更容易流动,电流剖面将演化得越来越集中在轴线上。这种偏离完全稳定的泰勒态的情况,为等离子体不稳定性提供了自由能来源,并最终激发足够大的撕裂模(tearing modes),使等离子体磁面变为遍历(ergodize),从而允许热量快速向外扩散。因此,电流剖面会重新平坦化,回到(近似)最小能量的泰勒态 [9]。这一过程不断重复,构成了所谓的 RFP 发电机效应( dynamo)。
相应地,引发这种发电机效应的芯部撕裂模有时被称为发电机模(dynamo modes)。
3.4 基本模型与方程
现在我们对 RFP 已有总体认识,接下来讨论所关注的问题。如第 2 章末尾所述,我们聚焦于一个大环径比、零 的 RFP 等离子体平衡态,其未受扰动的磁通面在极向平面中近似为同心圆。此类系统可很好地近似为周期性圆柱。采用标准的柱坐标 。假设系统在 方向具有周期性,周期长度为 ,其中 为等离子体的模拟大半径。为方便起见,定义模拟的环向角 。RFP 平衡磁场的形式为
其中
且(见式(3.24))
相应的平衡等离子体电流为
其中 表示对 的导数。
假设等离子体(小半径为 )被一个同心、薄且具有电阻的壳层包围,该壳层的小半径为 。而该电阻壳层又被一个同心、理想导体壳层包围,其小半径为 。因此,。假设导体壳层上存在狭窄的真空缝隙,允许静态的、外部产生的非轴对称误差场(error-field)渗入。我们的目标是研究此类误差场以及在电阻壳层中激发的螺旋涡流对典型芯部撕裂模(例如 模)旋转的影响。为简化起见,忽略等离子体中的所有其他模。上述条件符合实际情况:在大多数 RFP 等离子体中,用于弛豫过程的磁通守恒(理想导体)壳层并非完全密封,而是包含缝隙以允许平衡磁场穿透。真空容器通常位于磁通守恒壳层内部,出于实际考虑,其设计尽可能薄且具有电阻性。
与撕裂模相关的磁扰动远小于平衡磁场(通常 )。因此,在等离子体主体区域中,该扰动可由线性物理精确描述。线性化后的临界稳定理想磁流体力学(ideal-MHD)力平衡方程可写为:
其中 和 分别为扰动的磁场和等离子体电流(注意在本章中,,)。我们采用扰动量的常规表示形式:
其中 为整数。通常,实际(即物理)的扰动量由 的实部给出。为方便起见,定义:
结合安培定律和 [14],可对式 (3.29) 和 (3.26) 进行处理,将 的其余分量用 表示为:
其中,
我们假设 ,但 当然可取正值或负值。
式 (3.29) 可简化为纽科姆方程(Newcomb's equation)[46]:
其中
在 的极限下,纽科姆方程的正则解满足 (当 时)。注意,由式 (3.37) 可知,纽科姆方程在 有理面(即小半径 处)具有奇异性,该位置满足 ,其中
(注意,由式 (3.30) 可知,我们也可将 识别为 ,这是合理的。)这种奇异性并不令人意外,因为在推导式 (3.35) 时,我们忽略了等离子体的惯性和电阻率(见式 (3.29)),因此我们仅期望式 (3.35) 能在“外区”(outer region)充分描述等离子体行为,这一点已在上一章中讨论过。
3.5 真空解
我们可以在等离子体外部的真空区域()获得 Newcomb 方程的显式解,此时方程 (3.35) 简化为
上述方程与修正的贝塞尔方程
具有一定的相似性。该贝塞尔方程的通解为
其中 和 是标准的修正贝塞尔函数, 和 为任意常数。若我们定义
则利用方程 (3.40) 可知, 实际上满足真空中的 Newcomb 方程 (3.39)。因此,方程 (3.39) 的通解为
为方便起见,我们将利用修正贝塞尔函数的递推关系,将解表示为 和 的形式,而非其导数:
其中
对于特殊情况 ,最一般的真空解简化为
注意,在托卡马克装置中,与方程 (3.44) 类似的真空解是更为简单的 和 函数。事实上,托卡马克的排序只是 RFP 排序的一个子集,可通过取极限 得到 [27]。
3.6 电磁力矩
现在我们计算作用在 有理面上的磁岛链上的净电磁力矩。为简化起见,我们假设磁岛链仅在环向方向旋转,这一假设在 RFP 受到强极向流阻尼时是合理的 [47]。所需的力矩首先通过计算有理面上的通量面积分环向力矩得到,然后对该有理面进行积分。因此,
其中
假设电流在有理面上呈“片状”分布(即其径向分量可忽略),并注意到所有一阶量在磁通面积分后将消失,则该力矩可重写为
其中 ,,且
是一个复参数,用于度量在有理面上流动的 螺旋电流的幅度和相位。诚然,从式 (3.48) 到 (3.50) 的推导中我们省略了许多步骤,但需要注意的关键点是: 扮演了 的角色,而 则扮演了 的角色。注意,若 与 同相位,则不会产生力矩。这一现象的物理原因可通过考察磁通面积分后的力矩 来理解:若 与 相位相差 (即正交),则 将为零(例如 )。注意到 ,而 ,因此若 与 完全同相,则 与 将正交,从而导致力矩为零。
顺便指出,尽管我们仅在有理面上计算了磁通面积分的电磁力矩,但实际上,临界稳定(无惯性)的理想磁流体力学(MHD)理论要求此类力矩只能在理想 MHD 失效的区域形成 [42]。要理解这一点,需回顾临界稳定理想 MHD 满足 ,因此结合式 (3.49) 以及系统所假设的“环向性”,必然要求净力矩为零。该结果的物理直觉是:等离子体内部施加的力会导致局部等离子体位移,而这种位移会受到惯性和粘性阻力的抑制。然而,在临界稳定理想 MHD 中,惯性和粘性被视为可忽略。因此,等离子体内部施加的任何力都会导致等离子体发生位移,从而使得该力被抵消至零。(类似地,静止的理想导体内部的电场会激发电流,这些电流迅速重新分布电荷,使电场归零。)[53] 因此,电磁力矩只能在有理面附近形成,因为在那里临界稳定理想 MHD 理论失效。
3.7 等离子体本征函数
式 (3.50) 表明,我们现在应关注等离子体本征函数 的求解。该本征函数必须满足以下条件:(i) 在外部区域满足纽科姆方程 (3.35);(ii) 在原点附近行为良好,并在位于 处的理想导体壳处为零;(iii) 满足连续性约束 (即恒定 近似);(iv) 在电阻壳 () 处具有梯度不连续性,这是由该处激发的涡流所致。
不失一般性,可将本征函数分解为两部分,以阐明问题的物理本质:
其中 ()和 ()是复参数,分别确定 撕裂扰动在有理面和真空容器处的幅度与相位。只要各部分 和 的构造使得总本征函数仍满足上述所有约束条件,这种分解就是可行的。本征函数的物理意义将在下文解释。
注意, 总可表示为其幅度和相位的形式:
其中 表示撕裂扰动的实幅度, 是其相位,该相位根据“无滑移”约束演化。该约束源于标准 MHD 理论 [42],指出在非线性区域, 撕裂模将随等离子体在其自身的有理面上对流,因为等离子体无法穿越有理面附近磁岛链的分界线。因此,可将磁岛视为一个固体,被有理面上的等离子体带动。考虑到等离子体仅在环向方向旋转,为满足无滑移约束, 必须按如下方式演化:
其中 是等离子体在 有理面上的环向角速度。
我们现在考虑函数 ,它表示在半径为 处存在一个理想导体壳时的归一化撕裂模本征函数。具体而言, 是 Newcomb 方程 (3.35) 的一个实数解,该解在 时行为良好,并满足
此外,结合方程 (3.56) 以及 是 Newcomb 方程的一个行为良好的解这一事实,可得
注意,量
可被识别为标准的 撕裂模稳定性指数(即它是 的柱坐标等效形式, 定义见方程 (2.32)),其计算假设在小半径 处存在一个理想导体壳。图 3.3 展示了一个典型的撕裂模本征函数 。
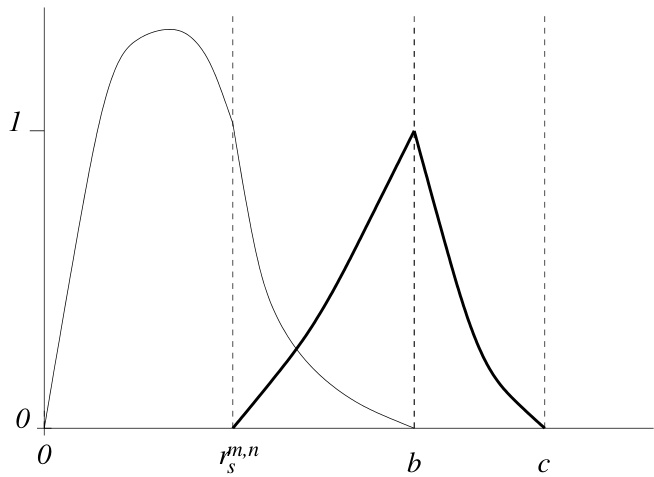
图 3.3:典型的相互作用本征函数 (粗体)和撕裂模本征函数 (非粗体)。
然而,位于 处的壳并非理想导体,这解释了方程 (3.52) 中第二项的出现,该项用于修正壳的电阻效应。一般来说,撕裂扰动会穿过电阻性壳泄漏出去,并由于其时变特性(回忆磁岛相对于静止壳在旋转),会在壳内感应出涡电流。由此产生的 力具有一个分量 ,试图推动壳沿等离子体旋转方向(即环向方向)运动;根据牛顿第三定律,在有理面处会产生一个反作用力 ,该力对等离子体旋转起到阻尼作用。注意,若壳为理想导体,则不会对壳施加任何力矩(因为该处磁场为零,故 )。因此,由于 (出现在方程 (3.52) 中)包含了所有由壳电阻引起的修正,我们称之为相互作用本征函数。
从数学上讲, 是 Newcomb 方程的一个实数解,满足
注意, 在 和 区间内为零。一般来说, 在 、 和 处具有梯度不连续性。边界条件 (3.59) 反映了如下假设:有理面上的等离子体能够产生足够大的扰动电流,从而完全屏蔽等离子体芯部免受壳中感应涡电流的影响,即 包含了对壳中涡电流的理想磁流体动力学(MHD)响应。图 3.3 也展示了一个典型的相互作用本征函数。
3.8 外解
类似于方程 (3.51),我们定义
这同样是一个复参数,用于确定在电阻性壳中流动的 涡电流的幅度和相位。利用方程 (3.52)、(3.51)、(3.62) 和 (3.58),我们将有理面和壳处的电流与这些位置上的 值联系起来:
其中
以及
注意,在通常情况下,、 和 均为实正数。根据纽科姆方程(3.35),我们可以写出
其中 ,。我们再次利用纽科姆方程,将相互作用本征函数用等离子体本征函数表示为
在等离子体外部的真空区域中,
其中 。由方程(3.66)、(3.67)和(3.69)可得
对于特殊情况 ,
从上述分析可以看出,匹配条件(3.63)–(3.64)中出现的所有实数量(即 、、、)均可通过已知的撕裂模本征函数 计算得出。
3.9 内区解——壳层物理
正如人们所预期的那样,若不包含内区物理,即 有理面和电阻壳层的物理效应,则外区方程(3.63)和(3.64)是不完备的。此处我们考虑壳层内部发生的情况。假设真空容器具有径向厚度 ,且满足 ,其电导率为 。壳层的 时间(即时间常数)定义为
相关方程仅为安培定律、法拉第定律和欧姆定律,将它们结合起来可得
我们限定在“薄壳”极限下,即扰动磁场在壳层中的趋肤深度远大于壳层厚度,但远小于其半径,亦即
在此极限下,等离子体本征函数 在壳层内几乎为常数,将方程 (3.74) 的 分量在壳层厚度方向上积分,可得
现在,根据方程 (3.52–3.53),我们知道在有理面上 的时间依赖关系为:
其中我们忽略了磁岛宽度 的缓慢时间变化。回顾 满足“无滑移”约束条件:
其中 是等离子体在 有理面上的环向角速度。若 近似为常数,则可预期 具有类似 的时间依赖性,此时方程 (3.76) 将给出电阻壳的一个简单色散关系:
将方程 (3.64) 与 (3.79) 结合,即可建立壳层处与有理面上 之间的关系:
注意,当 时,壳层中的涡流很大,穿透磁通很小。因此在此极限下,壳层实际上表现为理想导体。
当然,方程 (3.79) 和 (3.80) 仅是近似,因为一般情况下 是随时间变化的。此时,为求得 ,我们将方程 (3.64) 与 (3.76) 结合,得到
该方程很容易求解(例如通过格林函数法或积分因子法),得到
注意,为简化记号,我们定义了
并且使用了初始条件 。
粗略地说,式 (3.82) 表明电阻壁对撕裂模的“历史”具有“记忆”效应,其根本原因在于:撕裂模在某一时刻 感应出的涡流需要有限的时间才能衰减。在大多数聚变装置中,这种衰减速率相对于典型的等离子体旋转周期而言非常缓慢,因此壁实际上具有非常好的记忆能力。不幸的是,式 (3.82) 比式 (3.80) 难以处理得多,因此在本论文中我们将采用后者。然而,在继续之前,我们注意到一些初步研究允许式 (3.82) 中的 随时间变化,结果表明(正如人们所预期的那样),岛的动力学方程中会引入一个新的类似惯性的修正项。不过,这一修正似乎并未改变本论文的主要结论。
将式 (3.63) 与式 (3.80) 结合,我们可以将有理面上的电流与该处的磁通联系起来:
其中
最后,我们可以将式 (3.50) 与式 (3.84) 结合,得到由电阻壳中涡流引起的、作用于 有理面附近的环向电磁拖曳力矩:
3.10 误差场
在讨论了撕裂模与电阻壳相互作用的问题之后,我们现在引入误差场的影响。假设在没有等离子体和两个壳体的情况下,外部产生的误差场可通过函数 描述,满足 ,如式 (3.31) 所示。我们假设误差场源位于半径 处。此外,我们假设位于 处的理想导体壳上存在狭窄的缝隙,允许误差场泄漏通过。我们假设理想导体壳仅通过要求金属部分满足 来改变磁场,而在缝隙区域则不改变磁通函数。因此,误差场的 分量可表示为
其中积分在缝隙的角向范围上进行。注意 是一个复数量,类比于式 (3.53) 和 (3.54),它满足
其中 是误差场的环向角速度。对于静态误差场()的情形,我们可以写成
与式 (3.52) 对比可见,唯一新增的项是 ,它代表误差场的贡献,并且是满足以下条件的 Newcomb 方程的一个实解:
图3.4展示了所有三种典型的本征函数。注意,由式(3.90)可知,
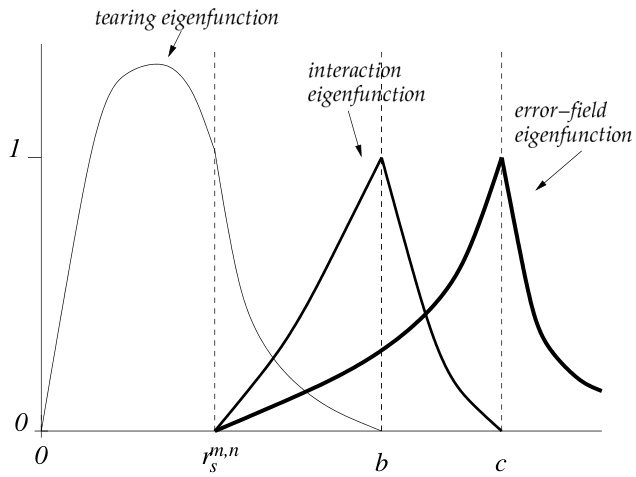
图3.4:典型的撕裂模、相互作用模和误差场本征函数
我们假设等离子体的磁通不会通过理想导体壳上的缝隙泄漏。只有当缝隙很窄时,这一假设才是一个较好的近似[14]。我们在有理面处的新匹配条件变为
其中 的定义类似于 (见式(3.65)):
类似于式(3.71),我们可以将 仅用撕裂模本征函数表示为
与上一节类似,我们可以利用壳层物理得出式(3.80)仍然成立,因此可以将式(3.94)改写为关于 和 的形式:
通常,我们可以结合式(3.50)和(3.97)得到电磁力矩:
其中我们使用了式(3.53)和(3.88)。该表达式将在下一章研究RFP中的模锁定行为时具有重要意义。
我们还将关注误差场随时间演化的情形,但在这种情况下,如上一节所述,电阻壳中激发的涡流变得相当难以计算。因此,为了简化问题,我们将通过令 (或等价地 )来移除中间的电阻壳。这种系统出现在研究撕裂模主动反馈的情形中。此时相关的力矩简化为
当 和 是任意时间函数时,上述表达式成立。
3.11 等离子体旋转
我们完整描述该问题所需的最后一个组成部分是:当等离子体被视为具有粘性的单一流体时,其所满足的流体运动方程。令 和 分别表示等离子体的环向角速度剖面和未受扰动的角速度剖面。因此,
其中 表示由电阻壁涡流和误差场引起的对 的修正。等离子体受扰动后的角运动方程是一个扩散方程,可写作 [42,49]:
其中 是等离子体的质量密度剖面, 是等离子体(反常)垂直于磁场方向的粘性系数剖面。注意,为简化起见,我们假设电磁力矩产生的非理想区域在径向上的宽度可忽略不计。受扰动的角速度满足如下边界条件:
在等离子体中心处,
以确保 在磁轴附近行为良好;而在等离子体边缘处,
使得边缘等离子体的速度被“钳制”住,不受在有理面附近产生的电磁力矩的影响。这一假设在文献 [42] 中得到了验证。我们将无滑移条件 (3.54) 重写为
其中 。电磁力矩(式 (3.98) 或 (3.99))、流体运动方程(式 (3.101))、受扰动速度剖面的边界条件(式 (3.102)–(3.103))以及无滑移条件(式 (3.104))共同构成了一组封闭的方程,可用于研究在存在电阻壁和误差场的情况下,RFP 中撕裂模的动力学行为。
最后,我们指出:若在有理面附近对流体运动方程 (3.101) 进行积分,并假设非理想区域的惯性可忽略,则可得
因此,我们可以将该方程左边识别为作用在磁岛链上的粘性力矩,在磁岛惯性可忽略的极限下,该粘性力矩必须与电磁力矩相平衡。通常,我们将通过求解如下方程来实现式 (3.101):
在除 以外的所有区域,并结合边界条件 (3.102) 和 (3.103)。由此得到的 通常在有理面处具有梯度不连续性,可用于计算粘性力矩。最终,我们按照式 (3.105) 平衡粘性力矩与电磁力矩。
第 4 章 RFP 中撕裂模的锁模现象
4.1 概述
在本章中,我们将应用上一章末尾推导出的方程,研究单个撕裂模与静态误差场以及电阻壁中激发的涡流相互作用的情形。这种情况与 RFP 中发电机模(即芯部撕裂模)的锁模行为密切相关。发电机模倾向于相互相位锁定 [14],形成一种环向局域化的磁结构,称为“弹簧模”(slinky mode)[15,16]。弹簧模会在面向等离子体的器壁表面产生一个环向局域化的“热点”,这很可能是因为混沌磁力线扩散所导致的径向输运在弹簧模振幅达到最大值的环向角度处达到峰值。由于弹簧模通常随等离子体在反转面处一起旋转,相应的“热点”类似于一个旋转的喷灯,不会长时间聚焦于器壁的某一特定区域。因此,仅就弹簧模本身而言,并不会严重损害等离子体的约束性能。然而,一旦弹簧模被静态误差场锁定,该静态热点将长时间停留在面向等离子体表面的同一位置,从而导致局部过热、杂质大量涌入等离子体,并最终引发放电提前终止 [27]。因此,弹簧模的锁模行为具有关键意义。
对聚变研究人员而言具有重要意义。在本章中,我们将通过考察单一螺旋撕裂模的锁模行为来获得深入理解。需要注意的是,一般来说,磁岛宽度的演化时间尺度远慢于相位演化的时间尺度,因此在本章中忽略岛宽的演化。
4.2 归一化
我们采用一种方便的归一化方式。令
,,,,,,,,
根据式 (2.69),以及
其中 ,而 在式 (3.38) 中已定义。典型的磁流体扩散和粘性扩散时间尺度可分别写为
注意,式 (4.3) 是式 (2.27) 的柱坐标形式。现在,令
此处, 和 分别代表归一化的模振幅和误差场振幅,在本章中将被视为输入参数。此外, 表示归一化的临界模速度,当模速度超过此值时,电阻壁开始表现得如同理想导体(参见式 (3.80));而 则衡量了未受扰动等离子体旋转周期与粘性扩散时间尺度之比。正如我们将看到的, 也可解释为归一化的临界模速度,当超过此值时,由误差场驱动的等离子体速度剖面的振荡分量将局域在有理面上。最后, 仅是一个方便的振幅标度。在通常情况下,参数 和 为 量级,而 、 和 则远小于 1。
扰动后的角动量方程 (3.101)、电磁力矩 (3.98)、扰动速度剖面的边界条件 (3.102–3.103) 以及无滑移约束条件 (3.104) 可重写为如下归一化形式:
这构成了我们完整的相位演化方程组。注意,为了方便起见,我们在式 (4.10) 中引入了
由于 与 仅相差一个 阶的因子,因此这两个量具有相同的物理意义。从现在起,为简化起见,我们假设 和 具有平坦的剖面。在此情况下,,所有关于粘性和密度的依赖性都包含在磁流体扩散时间尺度 和粘性扩散时间尺度 中。
4.3 相位演化方程简介
磁约束聚变装置中撕裂模动力学的标准描述,以 Zohm 等人的经典论文 [54] 为代表,体现在以下相位演化方程组中:
此处, 如前所述,表示模的归一化环向相速度; 是撕裂模相对于误差场的螺旋角; 是等离子体中(固定)区域的归一化环向转动惯量,该区域被假定与模共转( 是该区域的实际转动惯量)。式 (4.17) 中的第一项代表共转区域的惯性,第二项是由于与等离子体其余部分的粘性耦合所产生的恢复力矩,第三项表示由电阻壁中感应的涡流所产生的阻尼力矩,最后一项则是由外部误差场所产生的锁模力矩。尽管上述方程组通常没有解析解,但可以非常容易地进行数值积分,因此实验工作者在解释磁约束聚变实验中获得的模锁定数据时,广泛使用该方程组(或其密切相关的变体)[30,52]。
与 Zohm 方程 (4.16–4.17) 相比,我们的相位演化方程组 (4.10–4.14) 要复杂得多,构成一个耦合的偏微分方程(PDE)/常微分方程(ODE)系统。然而需要注意的是,式 (4.10) 具有理想(且物理上合理)的特性:与磁岛链共转的等离子体区域由粘性决定,因此随磁岛相速度而变化。换句话说,当磁岛减速时,被粘性拖曳而共转的区域宽度增大;当磁岛加速时,该区域宽度缩小。相比之下,Zohm 方程假设一个固定宽度的等离子体区域与撕裂模共转(通常取为相应磁岛链的宽度)。下一节的目标是将 PDE/ODE 系统 (4.10–4.14) 转化为一个(较小的)ODE 方程组,其数值积分难度几乎与 Zohm 方程相当,但仍允许通过粘性确定与磁岛链共转区域的宽度。
4.4 相位演化方程的推导
首先,我们注意到电磁力矩 (4.11) 只是涡流阻尼力矩与误差场力矩之和。在没有误差场的情况下,涡流阻尼力矩允许 存在一个稳态非零解;而误差场力矩在 非零时始终是振荡的。因此,我们尝试如下形式的解:
其中 是由涡流力矩的稳态分量驱动的扰动速度的稳态部分, 是振荡部分。我们进一步假设 是在没有误差场时计算得到的稳态扰动速度。因此,根据式 (4.10)、(4.12) 和 (4.13), 满足
除 外处处成立,并满足边界条件
以及匹配条件
此处, 是在存在电阻壁但无误差场的情况下,该模态的稳态(归一化)角速度。由方程 (4.19)–(4.21) 可得
其中 满足方程 (4.22):
上述方程是关于 的三次方程,它要么只有一个稳定的实根(即物理上有意义的根),要么有三个实根(其中两个是稳定的)。在后一种情况下,相关的根取决于初始条件(我们将在第 4.6 节中详细讨论)。因此,将该方程转化为一个动力学方程更为方便:
这里, 是一个正的常数,其取值旨在优化上述方程解向最终稳定不动点(依赖于初始条件)的收敛速度,该不动点等价于方程 (4.24) 的物理根。
方程 (4.18)、(4.23) 和 (4.24) 可与原始的相位演化方程 (4.10)–(4.14) 结合,得到一组以 表示的新相位演化方程:
其中 。
方程 (4.27) 表明,驱动 (即扰动等离子体旋转剖面的振荡分量)的电磁力矩由两部分组成:一部分是由误差场驱动的模态角速度 相对于其稳态值 的振荡所引起的涡流制动转矩的时间变化分量,另一部分是误差场引起的振荡力矩。后者的调制形式为 。在本章中,我们假设前者的力矩也以 的形式调制(我们将在下一章放松这一假设)。因此,我们假设
其中,当然,实际的解是上述表达式的实部。注意,我们必须在 中包含对 的依赖性,这大致可视为随磁岛一起拖曳的等离子体区域的(随时间变化的)包络。具体而言,若磁岛“缓慢”旋转,则我们预期随磁岛粘性拖曳的等离子体区域会“较大”;反之,若磁岛“快速”旋转,则磁岛会在等离子体中滑过,仅拖曳极少的等离子体。因此,当磁岛速度 因电磁力矩的振荡分量而调制时,我们预期扰动速度剖面的包络会“呼吸”——即随着 的减小和增大而变宽或变窄。
将式 (4.31) 代入式 (4.26),我们发现(除有理面 外的所有位置) 满足
注意,括号中的第一项与扰动速度剖面因快速变化的相位 而产生的时变有关,而第二项则描述了扰动速度剖面包络的时间变化。粗略地说,若速度 在一个振荡周期内的相对变化很小(即 ),我们可以忽略第二项,此时上述方程退化为贝塞尔方程:
式 (4.33) 的标准解为复宗量的贝塞尔函数:
其中 ,,而 和 是由边界条件确定的常数。注意,
其中 为实数,而 ber、bei、ker 和 kei 是标准的(实值)开尔文函数。
满足边界条件 (4.28–4.29) 并在有理面处连续的式 (4.33) 的解为
其中我们定义 。我们稍后会用到上述表达式,但现在先通过研究其极限行为来建立物理直觉。
在 (即 )的情形下,式 (4.37) 近似为
(这与式 (4.23) 中的形式相同);而在 (即 )的极限下,我们有
第一个表达式 (4.38) 表明,当模的旋转速度 远低于临界速度 时,由误差场驱动的扰动角速度剖面的振荡分量会遍布整个等离子体。另一方面,第二个表达式 (4.39) 表明,当 远大于 时,扰动速度剖面的振荡分量会局域在有理面附近。事实上,我们可以将式 (4.31) 与 (4.39) 结合,得到
在 近似为常数的情形下(即 ;参见式 (4.30)),上式可重写为
因此,在有理面 处来回振荡的电磁力矩会产生一个速度扰动,该扰动表现为一个正弦行波,以速度 从有理面向外传播。该波在向外传播过程中会衰减,这可由指数衰减因子看出,并且其局域在区域 内。
在本章中,我们假设磁岛宽度始终远小于振荡速度剖面的径向宽度。因此,决定与模共转的等离子体区域范围的始终是粘性效应,而非磁岛宽度。对于当今磁约束聚变装置中典型的磁岛宽度、模旋转速度以及动量约束时间尺度而言,这一假设是合理的 [27]。
在继续之前,我们注意到由式 (4.40) 可知,尽管 通常是随时间变化的,但包络函数 却对速度的变化作出瞬时响应。由于动量在等离子体中是通过扩散方式输运的,我们预期这种响应应存在时间延迟,且离有理面越远,延迟时间越长。式 (4.40) 中的这一缺陷并不令人意外,因为在推导 时,我们忽略了描述包络时间演化的项(见式 (4.32–4.33))。我们将在下一章修正这一瞬时响应的问题。
现在我们关注与 相关的粘性力矩。根据式 (4.26) 和 (4.31),我们可以将该力矩(以归一化形式)表示为(回顾式 (3.105) 后的讨论):
其中我们定义了
由式 (4.37) 可得
其中
并利用了 Wronskian 关系
我们稍后将使用上述 的表达式,但由于我们希望获得物理直观,再次考察其极限行为。利用式 (4.38) 和 (4.39),我们得到
现在,我们尝试用如下近似:
该近似至少在式 (4.47) 的两种极限情形下能还原为正确的表达式。
回到粘性力矩,由式 (4.42) 和 (4.44) 可得
其中我们已将 和 重写。目前,上述表达式看起来毫无意义,但回顾式 (4.30)、(4.31) 和 (4.37) 可知:
以及
在上式中,我们假设 的所有时间变化均由螺旋相位 的调制主导,而非振幅 或相位角 的变化。这一假设与我们之前的假设一致,即 相对于 很小(参见式 (4.32) 之后的讨论;我们将在下一章放松这一假设)。因此,
将式 (4.50) 和 (4.51) 代入式 (4.49),我们得到
因此,黏性力矩自然产生一个(由黏性决定的)惯性项 ,以及一个与 成正比的恢复力矩。通过式 (4.26) 将黏性力矩与电磁力矩匹配,可得
或者,利用式 (4.27)、(4.52) 和 (4.24),
利用 的简化形式(式 (4.48)),我们有
4.5 讨论
我们已将偏微分/常微分方程组 (4.10)–(4.14) 简化为以下四个耦合的一阶常微分方程组成的更简单系统:
物理动力学变量为 (相对于误差场相位测量的模的螺旋相位)和 (模的归一化相速度)。回顾式 (4.25),式 (4.58) 和 (4.59) 本身并无真实的物理意义。它们仅用于求解式 (4.24) 的物理根,而 是一个可选的、量级为 的正参数,没有直接的物理后果,仅用于便于上述方程的数值求解。需要注意的是,变量 被解释为在存在电阻壳但不存在误差场的情况下,撕裂模岛的稳态速度。参数 、、 在式 (4.5–4.7) 中定义,分别表示归一化的模振幅、归一化的误差场振幅,以及电阻壳开始表现得如同理想导体时的临界归一化相速度。
式 (4.57) 被解释为模的角运动方程,几乎包含了全部物理内容。第一项代表与模共同旋转的等离子体区域的惯性。第二项是由于有理面附近等离子体与扰动旋转剖面振荡分量之间的粘性耦合所产生的恢复力矩。第三项是由于有理面附近等离子体与扰动旋转剖面稳态分量之间的粘性耦合所产生的恢复力矩。第四项是电阻壳中感应涡流所产生的电磁制动转矩,最后一项则是由误差场所产生的电磁转矩。
注意,在极限 下,式 (4.56) 和 (4.57) 简化为:
可见 项已消失,因此式 (4.58–4.59) 不再必要。上述方程组与 Zohm 方程具有相同的形式。然而,对于当今反场箍缩装置(RFP)中典型的动量约束时间尺度和模旋转速度,参数 远小于 1 [26],此时应采用式 (4.56–4.59)。这些方程的优势在于,它们几乎与 Zohm 方程一样易于积分,同时还能自洽地计算与模共同旋转的等离子体区域的径向范围;该区域的宽度由等离子体粘性决定。
4.6 电阻壳制动与释放阈值
假设我们“关闭”误差场(即 )。在此极限下,相位演化方程大大简化(,),得到预期的稳态力矩平衡方程 (4.24):
其中 表示归一化的稳态粘性阻力矩 ,而右边项(带负号)表示归一化的稳态电磁力矩 。该问题已被相当广泛地研究过 [23–25, 42, 50, 51],此处仅给出要点。
电磁力矩随模速度 呈现出典型的非单调变化,如图 4.1 所示。
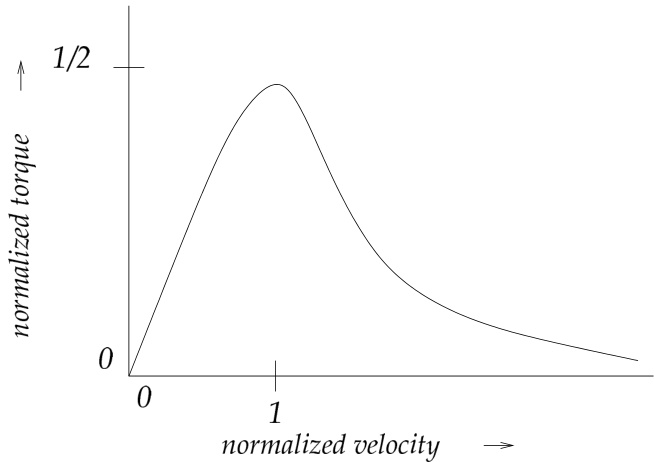
图 4.1:归一化电磁力矩 随归一化速度 变化的示意图。
为理解这一行为,我们回顾第 3.7 节的讨论:作用于撕裂模岛链的电磁力矩 (在大小上)等于作用于电阻壳上的 力矩。该力矩的产生原因是:旋转的撕裂模及其伴随的时间变化扰动磁场 在壳上感应出涡流 ,从而在壳上产生 力。当 时,壳上的力矩为零,因为撕裂模不旋转,壳中不会激发涡流。随着 增大,涡流增强, 力矩也随之增大;事实上,当 时,力矩与 呈线性关系。当 接近临界值 时,涡流开始将磁通从壳中排出(即 减小),力矩的增长速率开始趋于平缓。力矩在 处达到最大值 ,此后随着 继续增大而减小,因为磁通被壳排斥的效应开始占主导地位。当 时,力矩与 成反比。
现在,式 (4.62) 是关于 的一个具有实系数的三次方程,因此它要么有三个实根,要么有一个实根和一对共轭复根。实根对应物理解。“控制参数”为归一化模振幅 和归一化模速度 (当模速度超过 时,壳表现得如同理想导体)。对式 (4.62) 的分析 [27,51] 表明,在物理相关的区域 内,参数 对应三种情形:、 和 。在第一种情形下,三次方程 (4.62) 仅有一个实根,对应快速旋转分支:
此时模速度足够高,大部分磁通被排出壳外(即 ),因此电磁阻力矩相当弱。一旦 超过 ,式 (4.62) 就有三个实根。第一个对应上述快速旋转分支,第二个对应慢速旋转分支:
在此分支上,模速度足够低,使得模的本征函数能够穿透电阻壳,因此电磁力矩较大。第三个实根对应的模速度介于快速和慢速分支之间。然而线性分析表明,该根是不稳定的 [51],因此只有前两个根对应物理解。最后,当 时,式 (4.62) 再次仅有一个实根,此时对应慢速旋转分支。注意,由于在快慢分支之间的速度范围内不存在稳定解,因此存在一个(归一化)模旋转速度的禁带。
为了完善我们的物理图像,假设我们从一个非常小的磁岛开始,该磁岛位于快速旋转分支上。参见图 4.2。当我们增大模的振幅 (我们设想一种可以做到这一点的情形),旋转速度会平滑地减小,但仍保持在同一分支上。然而,一旦 超过电阻壳穿透阈值 ,快速旋转分支将不再存在,模态会跃迁到慢速旋转分支。如果我们此时减小 ,模的旋转速度会平滑加快,直到模振幅达到电阻壳释放阈值 ,此时慢速旋转分支消失,并迅速跃迁回快速旋转分支。由于通常 ,因此在电阻壳穿透/释放循环中存在显著的滞后效应。需要注意的是,上述理论结果最早在文献 [42] 中推导得出,随后在文献 [52] 中得到了实验验证。
4.7 误差场锁模与解锁阈值
现在假设我们“开启”误差场,但通过使壳层变得无限薄(即 ,或等价地 )来移除壳层。在这种情况下,我们的相位演化方程 (4.56–4.59) 简化为 、,以及
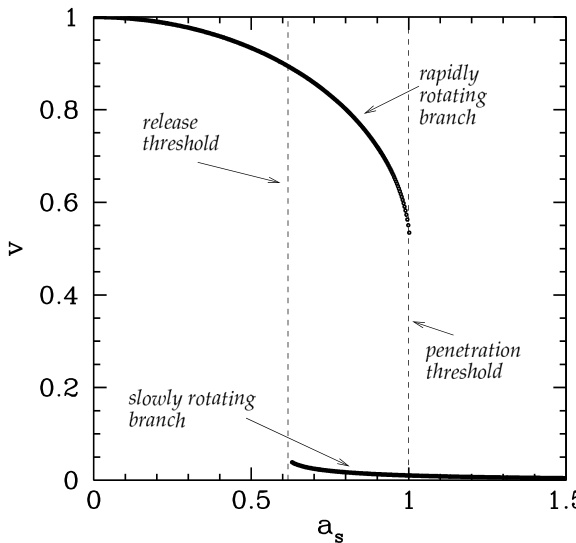
图 4.2:电阻壳穿透/释放循环的滞后图,计算参数为 。归一化的模旋转速度 作为归一化模振幅 的函数。
粗略地说,方程 (4.66–4.67) 类似于一个在周期势场 (第三项)中运动的小球,同时受到沿正 方向以速度 吹拂的微风(第二项)的作用。因此,若小球以速度 滚动,风会使其减速;若 ,风则会加速小球。假设小球初始速度为 。若势场振幅 非常弱,我们预期小球将以 的速度滚动,仅在经过势谷和势垒时略有加速或减速。然而,若 过大,小球将没有足够能量翻越势垒,最终会停止运动。
基于这一类比,方程 (4.66) 和 (4.67) 支持两类解,这与之前考虑的撕裂模与电阻壁相互作用的情形类似。第一类是旋转分支,此时模以速度 旋转,该速度受振荡的误差场力矩调制;第二类是锁模分支,此时模被锁定在误差场上,即 ,方程 (4.67) 简化为
该式用于确定锁模角度 。图 4.3 展示了这些解的特性。
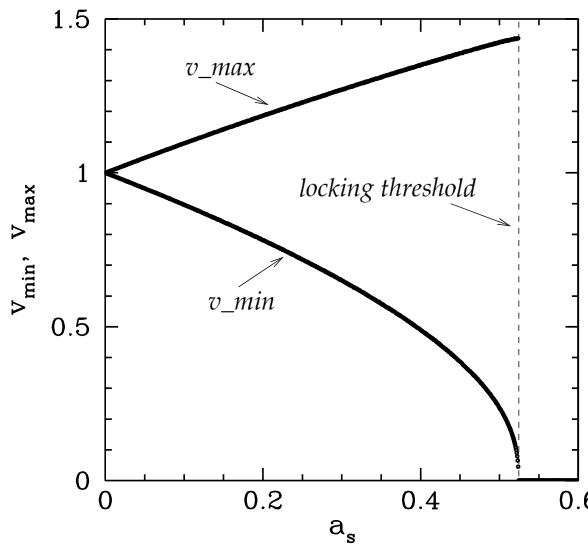
图 4.3:旋转分支的解,计算参数为 和 。归一化模旋转速度 的最大值和最小值作为归一化模振幅 的函数。
对于非常小的 (或等价地非常小的 ;关键在于电磁力矩要足够小),磁岛起始于旋转分支,以略偏离 的速度旋转。随着 增大,由误差场驱动的速度振荡幅度逐渐增大,直到误差场力矩达到临界值
此时旋转分支不再存在,模态切换至锁模分支。从物理上看,当误差场对磁岛施加的电磁力矩超过等离子体提供的粘性恢复力矩时,磁岛便被锁定在误差场上。为理解这一点,我们将运动方程 (4.67) 在 极限下(适用于旋转分支)重写为:
其中,第三项代表的电磁力矩可以任意大,但第二项代表的粘性恢复力矩在磁岛被电磁力矩减速时所能提供的(加速)恢复力矩是有限的。事实上,粘性力矩存在一个最大值(在 处)。因此,一旦电磁力矩超过该最大值,粘性力矩与电磁力矩将无法再平衡,磁岛便被锁定在误差场上。
需要注意的是,模锁模阈值 (4.69) 是通过数值计算确定的,实际上对 的依赖非常弱。还需注意,旋转分支的消失对应于误差场将模的最小速度降低至零的点。然而,正如我们稍后将看到的,当考虑磁岛宽度演化(Rutherford 方程)或速度扰动剖面的演化(即方程 (4.32) 中的 项)时,磁岛通常会在 之前就发生锁模。
图 4.4 展示了锁定解分支的特性。随着归一化模振幅 的减小,锁定角 增大。根据式 (4.67),当 与 的乘积低于误差场解锁阈值时,
锁定解分支将不复存在,模态将切换至旋转分支。注意,锁定解分支的消失对应于锁定角 达到 的点。
观察式 (4.69) 和 (4.71) 可知,在物理上相关的区域 中,解锁阈值显著小于锁定阈值,因此在误差场的锁定/解锁循环中存在明显的滞后现象。我们回忆起,在此前考虑的撕裂模与电阻壁相互作用的情形中,也观察到了类似的滞后现象。在那种情况下,滞后的根源可追溯至电磁力矩的非单调特性;而在此处,
滞后的根源则是随着速度 的变化,与模共转的等离子体区域宽度发生剧烈变化。我们将在下一章对此进行详细说明。
4.8 电阻壁修正的误差场锁定与解锁阈值
我们现在考虑撕裂模同时与电阻壁和误差场相互作用的完整问题。基于前两节所建立的物理直觉,我们可以大致预期三种类型的行为。如果归一化磁岛振幅 非常小,则壁面力矩()和误差场力矩()都太弱,不足以将磁岛锁定,因此我们将得到一个快速旋转的模,其归一化速度在 附近受误差场调制。对于较大的磁岛振幅()和较弱的误差场(),我们预期电阻壁的阻尼力矩占主导地位,因此得到一个缓慢旋转的模,其归一化速度 在 附近受误差场调制(回顾 4.6 节可知,在缓慢旋转分支上,速度不能超过 )。在强误差场()存在的情况下,我们预期误差场足够强,能够将旋转磁岛锁定,从而形成一个静止的、被误差场锁定的模。
我们可以对完整的相位演化方程组 (4.56–4.59) 进行数值积分,得到图 4.5 所示的示意图。该图在物理上相关的区域 内有效,展示了 空间中各类阈值曲线的大致位置。注意,这些曲线的位置是通过数值方法确定的。标记为 2 的曲线是
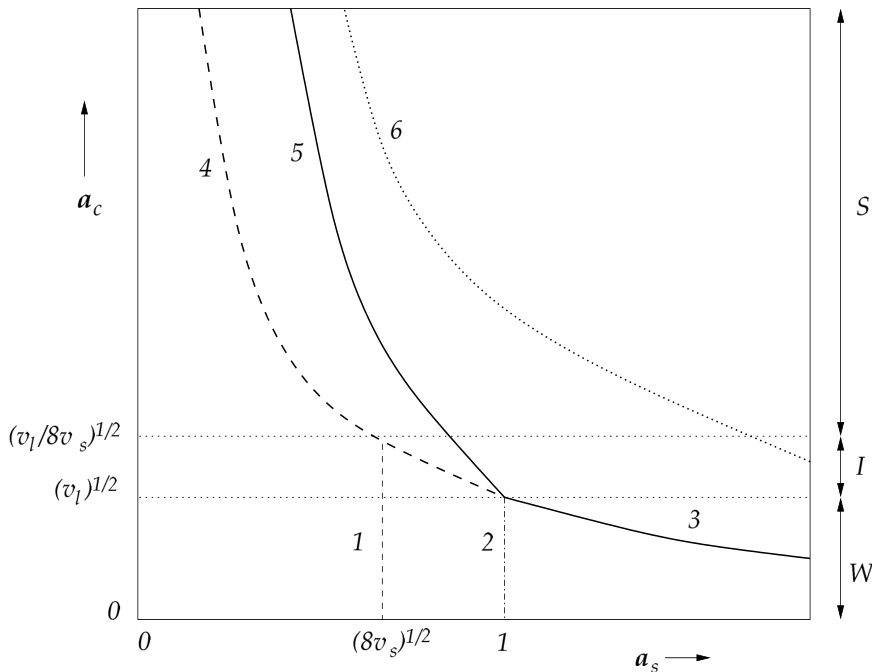
图 4.5:示意图展示了在存在电阻壁和静态误差场的情况下,各类阈值曲线在归一化模振幅 与归一化误差场振幅 空间中的分布。曲线 1 是电阻壁释放阈值;曲线 2 是电阻壁制动阈值;曲线 3 是联合误差场锁定与解锁阈值;曲线 4 是误差场解锁阈值;曲线 5 是误差场锁定阈值;曲线 6 是无电阻壁时的误差场锁定阈值。图中还标出了强(S)、中等(I)和弱(W)误差场区域的范围。
电阻壁锁定阈值,表示从快速旋转解向缓慢旋转解的转变。该曲线的近似公式为:当 时,。标记为 3 的曲线是联合误差场锁定与解锁阈值,表示缓慢旋转解与误差场锁定解之间的边界。当 时,曲线 3 可近似表示为 。曲线 5 在 时可近似表示为 ,是另一条误差场锁定阈值曲线,表示从快速旋转解向误差场锁定解的转变。曲线 4 在 时可近似表示为 ,是
误差场解锁阈值,表示从误差场锁定解向快速旋转解的转变。曲线 1 在 时可近似表示为 ,是壁面释放阈值,表示从缓慢旋转解向快速旋转解的转变。最后,曲线 6 由 给出,是无电阻壁时的误差场锁定阈值。
注意,误差场解锁阈值曲线(图 4.5 中的曲线 3 和 4)的位置不受电阻壁存在的影响。这一结果是可以预期的,因为电阻壁无法对误差场锁定模施加任何力矩(其对应的速度为零),因此不会影响误差场解锁边界。另一方面,在存在电阻壁的情况下,误差场锁定阈值(曲线 3 和 5)的位置与无壁情况(曲线 6)不同。事实上,我们可以看到,在存在电阻壁的情况下,触发向锁定模转变所需的乘积 的临界值总是降低的。因此,正如预期的那样——因为电阻壁力矩始终起到减缓模速度的作用——电阻壁充当了误差场锁定模形成的催化剂。顺便指出,“催化剂”一词在此处是恰当的,因为一旦模被误差场锁定,电阻壁在模的动力学中就不再起任何作用。
图 4.5 表明,归一化误差场振幅 自然地可分为三个宽泛的区域。弱误差场区域对应于
中等误差场区域对应于
最后,强误差场区域对应于
现在让我们分别研究这三种区域。
4.8.1 弱误差场区域
图 4.6 展示了弱误差场区域的典型行为。当归一化模振幅 非常小时,该模处于快速旋转解分支上。此时,磁岛以归一化速度 旋转,该速度在图 4.6 所示的最小值与最大值之间快速振荡。当 增大并超过电阻壳穿透阈值(图 4.5 中的曲线 2)时,电阻壳产生的力矩变得足够大,使得磁岛从快速旋转分支跃迁到慢速旋转分支。当 进一步增大并超过误差场锁模阈值(图 4.5 中的曲线 3)时,磁岛会再次跃迁到锁模分支。反之,若从较大的初始 值开始减小,则当达到误差场解锁阈值(图 4.5 中的曲线 3)时,该模会从锁模分支跃迁回慢速旋转分支;当进一步减小至电阻壳释放阈值(图 4.5 中的曲线 1)时,该模会再次跃迁回快速旋转分支。注意,在弱误差场区域中,电阻壳穿透/释放循环存在滞后现象,但误差场锁模/解锁循环则没有滞后。
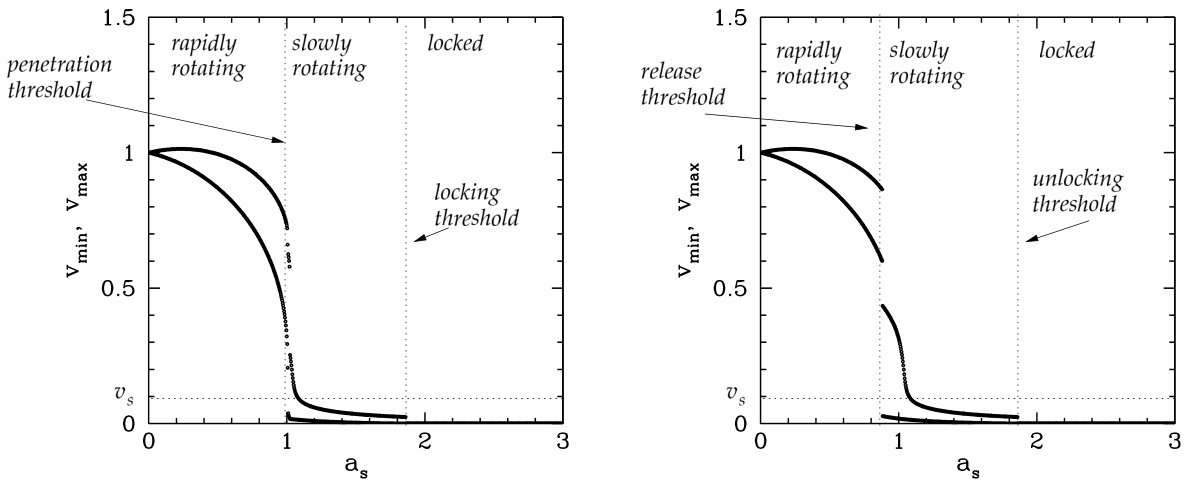
图 4.6:弱误差场区域。归一化速度 的最大值和最小值作为归一化模振幅 的函数被绘出,参数为 、 和 。分别展示了 增大和减小的情形。
为了帮助理解误差场锁模/解锁循环中滞后现象的意外缺失,我们在图 4.7 中绘制了一个靠近误差场锁模阈值(即参数空间中的 )的慢速旋转模的相位和速度。可以看出,该模是间歇性旋转的。换句话说,磁岛持续旋转,直到误差场在 (其中 为任意整数)时“抓住”它(见图 4.7 中的点 ;同时回顾误差场锁模力矩正比于 )。由于误差场太弱,无法完全阻止磁岛的运动,因此磁岛最终能够越过最大锁模力矩对应的角度 。此时,磁岛迅速绕行一周( 完成一次完整旋转),随后再次在角度 处被误差场“卡住”(见图 4.7 中的点 ),循环重新开始。当在参数空间中趋近误差场锁模阈值时,这些间歇性旋转事件之间的时间间隔迅速增大,并在达到阈值时趋于无穷大。因此,当跨越误差场锁模/解锁阈值时,慢速旋转模与锁模之间的转变是完全可逆的(即无滞后)。总之,在弱误差场区域中,电阻壳对锁模形成的催化作用非常有效,以至于一旦物理上允许锁模解存在(即一旦跨越误差场解锁边界),锁模便立即形成。
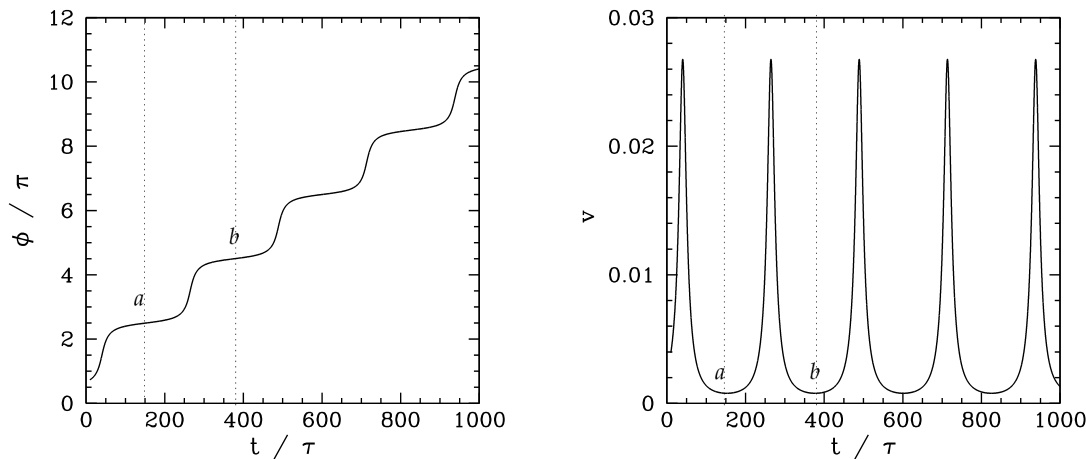
图 4.7:靠近误差场锁模阈值的慢速旋转解。相位 和归一化旋转速度 被绘为 的函数,其中 为未受扰动时的模旋转周期,参数为 、、 和 。
4.8.2 中等误差场区域
图 4.8 展示了中等误差场区域的典型行为。与弱误差场区域类似,当 非常小时,磁岛处于快速旋转解分支上。一旦 超过锁模阈值(图 4.5 中的曲线 5),该模会直接跃迁到误差场锁模状态。若此时减小 ,磁岛将保持锁模状态,直到 降至误差场解锁阈值(图 4.5 中的曲线 4)以下,此时磁岛会切换到慢速旋转解分支。当进一步减小 并越过电阻壳释放阈值(图 4.5 中的曲线 1)时,解会跃迁回快速旋转分支。注意,在中等误差场区域中,
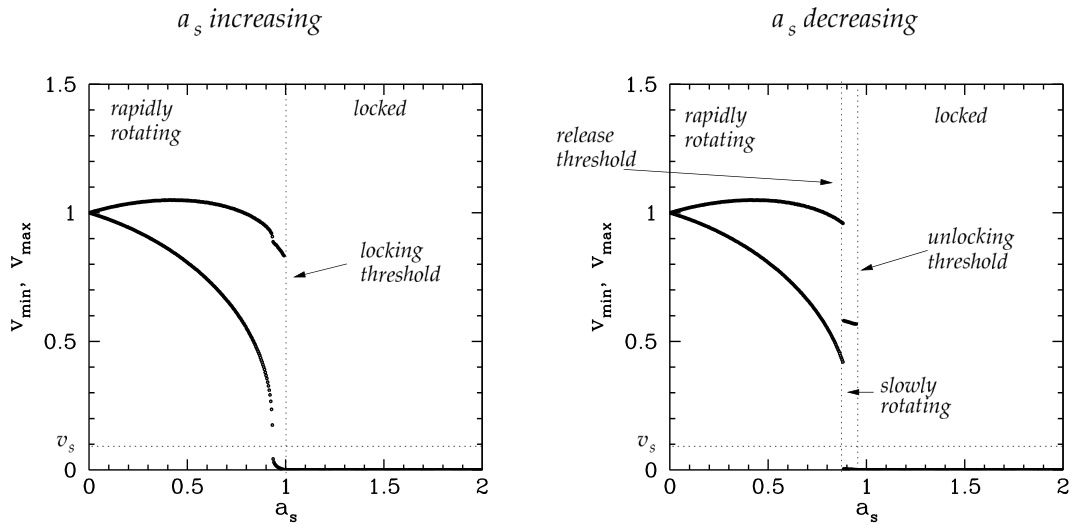
图 4.8:中等误差场区域。归一化速度 的最大值和最小值作为归一化模振幅 的函数被绘出,参数为 、 和 。分别展示了 增大和减小的情形。
慢速旋转解分支仅在 减小时可达。此外,此时误差场锁模/解锁循环中已出现少量滞后现象。
4.8.3 强误差场区域
图 4.9 展示了强误差场区域的典型行为。当 从很小的初始值开始增大时,该模起初处于快速旋转分支,但一旦跨越误差场锁模阈值(图 4.5 中的曲线 5),便会直接跃迁到误差场锁模状态。注意,该锁模阈值对应于 的点(在 空间中)。
如前所述,更精确的处理将表明,实际上磁岛在 之前就已经锁模。现在若减小 ,该模将保持与误差场锁模,直到 跨越误差场解锁阈值(图 4.5 中的曲线 4),此时模会跃迁回快速旋转分支。注意,在
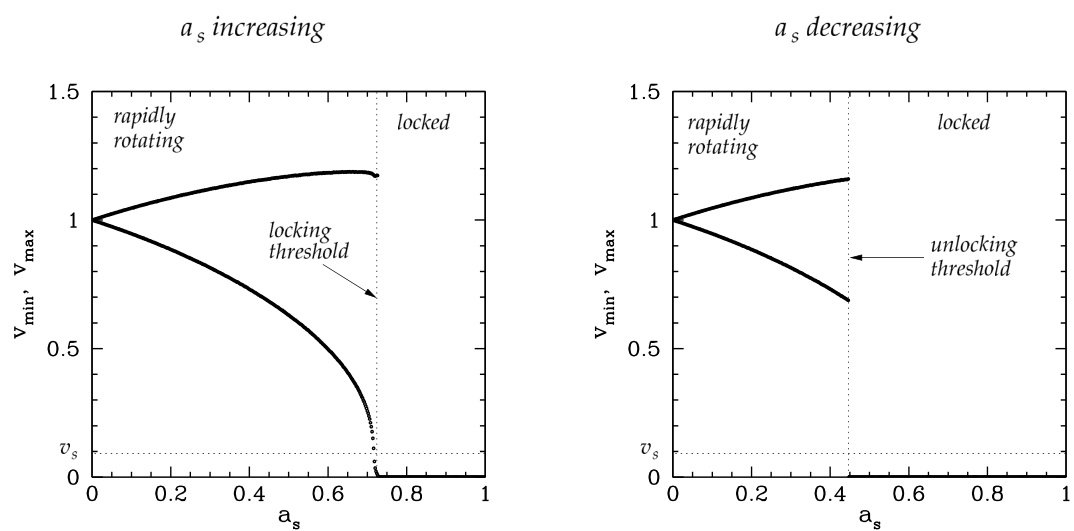
图 4.9:强误差场区域。归一化速度 的最大值和最小值作为归一化模振幅 的函数被绘出,参数为 、 和 。分别展示了 增大和减小的情形。
强误差场区域中,慢速旋转解分支已不复存在。此外,误差场锁模/解锁循环中存在显著的滞后现象。事实上,从图 4.5 可以看出,当归一化误差场振幅 超过临界值 后,电阻壳在误差场锁模阈值(图 4.5 中的曲线 5)中的作用逐渐减弱,最终误差场锁模阈值与无电阻壳情况下的计算结果(图 4.5 中的曲线 6)趋于一致。
4.9 小结
我们研究了在存在电阻真空容器和外部误差场的情况下,单个 非线性撕裂模的动力学行为。首先,我们推导出一组相位演化方程(4.10–4.14),描述了撕裂模相位在电阻真空容器中感应涡流产生的制动力矩和外部误差场产生的锁模力矩共同作用下的演化过程。遗憾的是,这些方程较为复杂(构成一个耦合的偏微分-常微分方程系统),实验人员在解释数据或设计新型 RFP 装置时难以方便地进行数值积分。
我们的下一步工作是通过一系列近似,将复杂的方程(4.10–4.14)简化为一组易于积分的常微分方程(4.56–4.59)(见第 4.4 节)。这些方程是对著名的 Zohm 方程的扩展,其中我们自洽地计算了与模共转的等离子体区域的径向范围,该区域的宽度由等离子体粘性决定。
最后,在第 4.8 节中,我们对式 (4.56–4.59) 进行了数值求解,以全面研究电阻式真空容器对误差场锁模和解锁阈值的影响。我们的研究结果汇总于图 4.5 中,该图展示了在模振幅与误差场振幅空间中各种阈值曲线的位置。可以看出,由于电阻式真空容器产生的阻尼力矩对误差场解锁阈值没有影响(这并不令人意外,因为在误差场锁模状态下,阻尼力矩为零),但总是促进误差场锁模(即降低误差场锁模阈值)。事实上,在图 4.5 所示的弱误差场区域中,一旦锁模在物理上成为可能(即一旦超过误差场解锁阈值),电阻壁就允许模立即锁定到误差场上。相比之下,若不存在电阻式真空容器,则误差场锁模阈值显著高于误差场解锁阈值。
4.10 有限差分方法
为了研究我们在第 4.4 节中所提出方法的有效性,我们需要一种能够直接积分“原始”相位演化方程(4.10–4.14)的方法,且不作任何近似。为方便起见,我们将这些方程重写如下:
为了对扩散方程 (4.75) 进行数值积分,我们将等离子体(其范围从 到 )划分为 个同心环,其中第 个环的中心位于 ,占据的空间为 (见图 4.10)。注意,我们将最内层的环标记为 。在每个环内(例如第 个环),我们假设归一化的扰动速度 、归一化的粘度 和归一化的等离子体密度 均为常数,分别等于 、 和 。不过,为简化起见,我们仍将限制自己采用平坦的粘度和密度剖面(即对所有 ,均有 )。

图 4.10:将等离子体划分为“环”以方便对相位演化方程进行数值积分。
我们可以通过引入一个中心位于 的额外环(见图 4.10)并令 来满足等离子体中心处的边界条件(式 (4.77))。类似地,通过引入另一个中心位于 的环并令 ,可满足等离子体边缘处的边界条件(式 (4.78))。需要注意的是,我们只关心位于等离子体内部的那些环(即索引 的环);中心位于 和 的环仅用于满足边界条件。
现在,将方程 (4.75) 在第 个环()上积分,可得:
其中我们使用了如下简单近似:
此外,由式 (4.80) 中的 Kronecker delta 可知,电磁力矩 仅作用于包含有理面的环(我们将其记为第 个环)。我们可以对方程 (4.80) 稍作整理,得到:
上述方程是我们对偏微分方程(4.75)的离散化形式,描述了通过电磁力矩在有理面上诱导的速度扰动如何通过粘性扩散到等离子体其余部分。
总结来说,我们已将相位演化方程(4.75–4.79)重写为 个耦合的常微分方程,分别表示每个环的运动方程:
相位的运动方程:
以及两个边界条件:
注意,上述方程组(4.83–4.86)使我们能够在不依赖推导简化相位演化方程(4.56–4.59)时所用假设的情况下(见第 4.4 节),对相位演化方程(4.75–4.79)进行积分。然而,为了准确模拟等离子体运动,我们预计 需要取较大值。因此,之前我们仅有四个耦合常微分方程(4.56–4.59),而现在则有 个耦合常微分方程,导致积分过程会慢得多。
4.11 简化相位演化方程的问题
现在,让我们利用上一节开发的方法(虽然计算较慢,但能非常精确地积分相位演化方程),检验简化相位演化方程(4.56–4.59)在多大程度上能够准确描述撕裂模动力学(本质上总结于图 4.5)。在图 4.11 中,我们绘制了锁模阈值曲线:即误差场锁模阈值(图 4.5 中的曲线 5)、电阻壁制动阈值(图 4.5 中的曲线 2),以及组合的误差场锁模/解锁阈值(图 4.5 中的曲线 3)。实线是采用有限差分(FD)方法计算得到的,而虚线则是使用简化相位演化方程(4.56–4.59)(即 ODE 方法)计算得到的。可以看出,除在描述从快速旋转模态向误差场锁模态转变的边界附近外,两种方法的结果非常吻合。具体而言,更精确的 FD 方法总是比 ODE 方法预测的更早发生锁模(图 4.11 中曲线 1 早于曲线 4)。
事实上,ODE 方法预测的锁模转变与 FD 方法的结果并不一致。在图 4.12 中,我们展示了图 4.9 的 FD 方法对应结果;图 4.9 使用 ODE 方法绘制了最小和最大速度随归一化撕裂岛宽度 的变化关系。对比这两幅图可见,FD 方法不允许最小速度平滑地降至零(如图 4.9 所示),而是一旦最小速度降至某一阈值以下,模态即发生锁模。在图 4.12 中,我们展示了使用 FD 方法计算的、分别位于锁模阈值下方和阈值上的 值对应的撕裂岛行为。
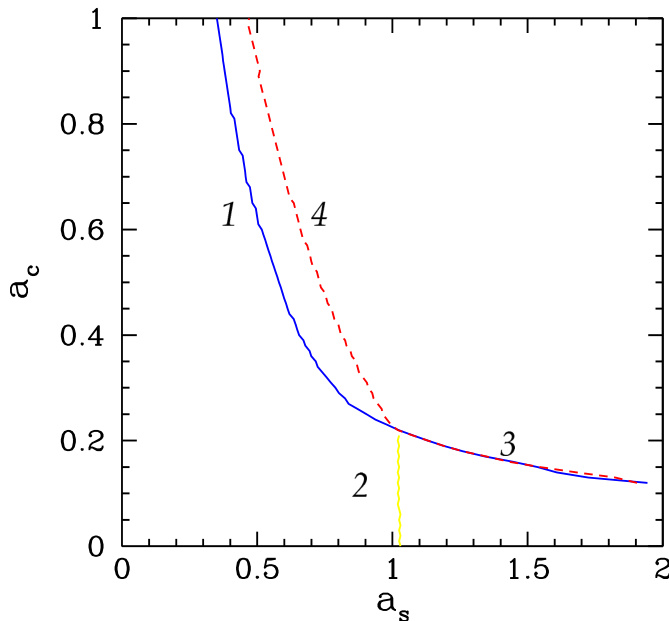
图 4.11:使用有限差分(FD)方法与 ODE 方法计算的锁模边界差异。曲线 1 是使用 FD 方法计算的误差场锁模边界,而曲线 4 是使用 ODE 方法计算的同一边界。曲线 2 为电阻壁制动阈值,曲线 3 为组合的误差场锁模/解锁阈值;在这两条曲线上,FD 与 ODE 方法结果一致。
注意,快速旋转分支的最小速度不能任意接近零。这与 ODE 方法预测的行为形成对比(见图 4.14):ODE 方法允许在 接近锁模边界时,快速旋转分支的最小速度任意接近零。显然,简化的 ODE 方程无法复现图 4.13 所示的、锁模发生前平均速度的缓慢下降过程。
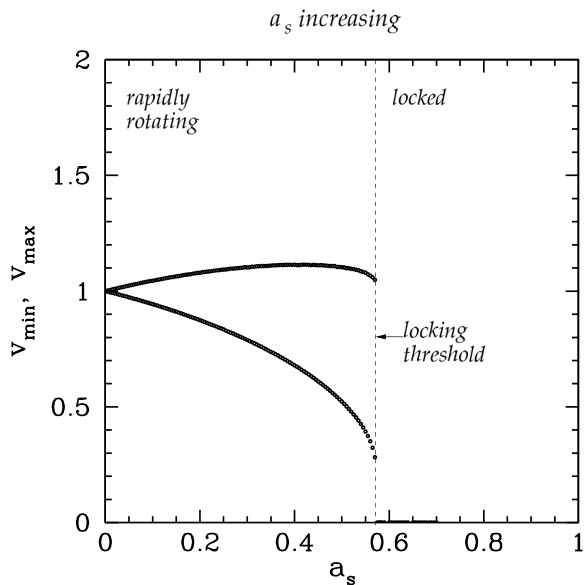
图 4.12:在强误差场情形()、、 和 条件下,使用有限体积方法绘制的最小和最大速度随归一化振幅 的变化关系。
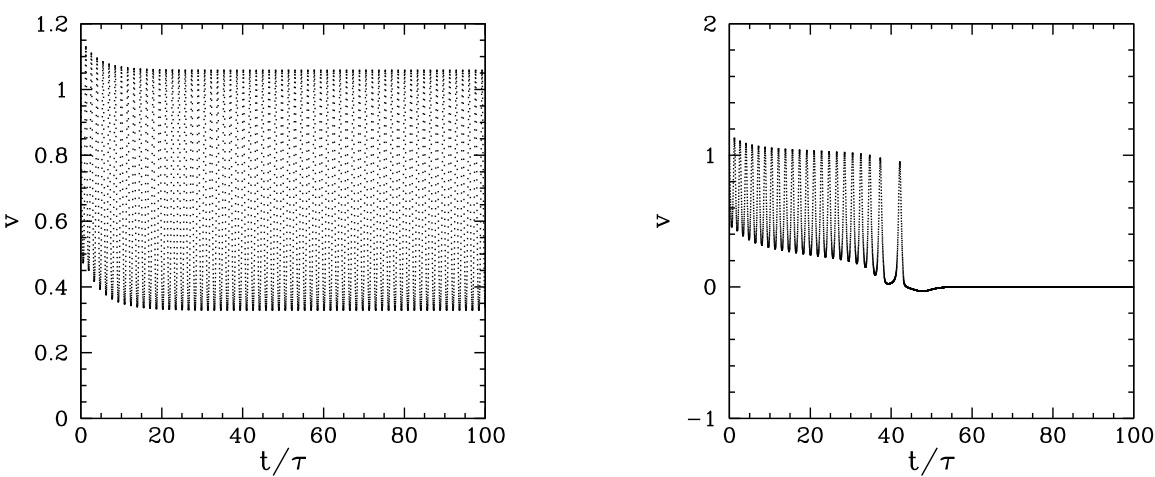
图 4.13:使用有限差分方法绘制的归一化撕裂岛相速度随时间的变化。左图对应 略低于锁模阈值的情形(,(强误差场情形),,,);右图对应趋近锁模的情形(,其余参数相同)。
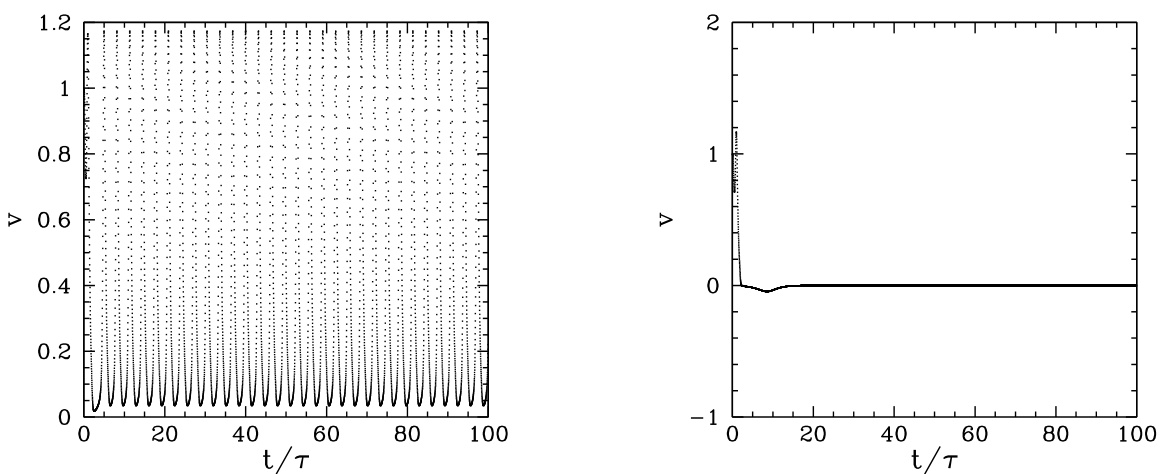
图 4.14:使用简化相位演化方程绘制的归一化撕裂岛相速度随时间的变化。左图对应 略低于锁模阈值的情形(,(强误差场情形),,);右图对应趋近锁模的情形(,其余参数相同)。
第 5 章 瞬态行为的引入
5.1 概述
正如我们在上一章末尾所看到的,我们简化的相位演化方程(4.56–4.59)并非没有缺陷。在本章中,我们将向解中引入类似瞬态的项,从而得到一组新的相位演化方程,这些方程不再包含上一章所述的近似和问题。随后,我们将注意力转向更简单的情形:撕裂模仅与误差场相互作用,但将以更一般的方式处理该问题。具体而言,我们将允许磁岛演化、误差场幅度演化以及误差场旋转。通过研究时变撕裂模与时变误差场相互作用的一般问题,我们将能够对磁反馈实验进行建模。
5.2 改进的相位演化方程
5.2.1 概述
让我们回顾一下问题。根据方程(4.75–4.78),我们需要找到满足以下条件的 :
请注意,上述所有量均为实数,但正如第 4.4 节中所做的那样,我们发现允许 为复数更为方便。由于上述方程在 中是线性的,我们只需在最后取 的实部即可得到物理解。
此前,我们假设
其中 是在无误差场情况下由电阻壳制动转矩引起的扰动角速度剖面。该解的形式基于物理考虑:即扰动速度剖面围绕一个由电阻壳转矩(在无误差场时)决定的恒定值振荡。正如我们在第 4.4 节中所见,只要做出若干假设,方程(5.4)就能满足方程(5.1–5.3)的所有要求,甚至可以得到 的解析表达式:
- 我们假设壳制动转矩的时变分量按 调制,即
- 我们假设 的时间变化主要由相位 的时间变化主导,即在
中,我们忽略了第一项。然而,正如第 4.4 节所讨论的,该项描述了扰动速度剖面的时间演化,忽略它会导致速度剖面具有非物理的特性——即对速度变化的响应是瞬时的。
- 我们使用了粘性转矩 的近似形式(见方程(4.48))。事实证明,近似的相位演化方程(4.56–4.59)在描述动力学行为方面表现相当好,除了在误差场锁模边界附近。然而,为了完整性,我们现在将扩展先前的解法(5.4),以摆脱上述所有假设。由此得到的相位演化方程将不如(4.56–4.59)那样简洁,但将是完全自洽的。
5.2.2 解的新形式
受参数变易法思想的启发,我们假设速度扰动具有如下形式:
注意,第一项与式 (5.4) 相比仅增加了对 的依赖性,其余部分保持不变。正如我们将看到的,这种依赖性对于满足式 (5.1) 和 (5.2) 是必要的,因为从比较式 (5.7) 与 (5.4) 可知,我们已省略了 。关于式 (5.7) 中新增的第二项,其中 是(目前尚未确定的)含时系数,而 是齐次扩散方程 (5.1) 的解。具体而言, 满足
为满足边界条件 (5.3),我们要求
这些解具有可分离变量的形式:
其中
此处 为任意常数, 是通常的零阶贝塞尔函数,而 满足
其中 是 的第 个零点。回顾 满足正交性条件:
其中 是一阶贝塞尔函数。为方便起见,我们对 施加归一化条件:
在此情况下,根据式 (5.11) 和 (5.13), 变为
将式 (5.7) 代入式 (5.1),我们发现除有理面外,在所有位置均有
注意,方程左边最后一项与右边最后一项因 是齐次方程的解而相互抵消。现在,在第 4.4 节中,我们假设 的时间变化(即式 (5.16) 的左边)由第一项主导。只有在这种情况下,我们才能得到 的闭式解,因为此时式 (5.16) 简化为
其具有开尔文函数解。我们新形式解的优点在于,仍可要求方程 (5.17) 成立(从而获得 的闭式解),同时通过设定以下关系,将方程 (5.16) 左侧先前被忽略的项纳入考虑:
注意,若方程 (5.17) 和 (5.18) 成立,则方程 (5.16) 自动满足。利用方程 (5.10)、正交条件 (5.14) 以及方程 (5.18),我们得到
其中
因此,我们已完全用剖面 表达了 ,而 将在下一节中确定。现在,我们可以将 视为一组新的动力学变量,并与 和 一同进行积分。
在继续之前,让我们回顾一下我们的解的形式 (5.7)。可以看出,扰动后的速度剖面由两部分组成。方程 (5.7) 中的第一项在第 4.4 节中已熟悉;若不存在壳层的复杂影响,
该解已相当准确。然而,一个主要问题是:速度剖面(由 决定)对作用在有理面上的电磁力矩作出瞬时响应。由于动量在等离子体中以扩散方式输运,我们预期响应存在时间延迟,且离有理面越远,延迟时间越长。方程 (5.7) 中的第二项代表问题的瞬态解,这些解会因粘性而自然衰减,但会被速度(及相位)的变化所激发。通过包含第二项,我们自洽地考虑了 的时间变化。具体而言,尽管从方程中无法直接看出,但后续的数值积分将表明,引入这些瞬态项确实为问题引入了所需的时间延迟。
5.2.3 的显式形式
现在回顾第 4.4 节,我们已用开尔文函数求得了 的表达式(见方程 (4.37)),仅剩一个未定常数 ,即 在有理面上的值。我们可通过在有理面附近积分方程 (5.1) 来确定 ,并如常假设磁岛惯性可忽略,从而得到
为方便起见,我们将其改写为复数形式:
由于 是齐次方程 (5.8) 的光滑解,无法支持梯度的不连续性,因此匹配条件完全由假设解 (5.7) 中的第一项 承担:
利用方程 (4.44),上式变为
其中 由方程 (4.45) 给出,且我们记得 。为使等式成立,我们将 分解为两部分:,并选取
(这也解释了为什么我们希望在方程 (5.7) 中的 里包含 依赖项),以及
最后,结合方程 (4.37)、(4.45)、(5.25) 和 (5.26),我们可以将 表示为
其中
5.2.4 计算 与瞬态振幅
我们现在可以计算方程 (5.20) 中定义的系数 。由方程 (5.20) 和 (5.27) 可知,
其中
利用方程 (5.28) 和 (5.15),我们可以将 显式地改写为
其中
以及
幸运的是,我们可以显式地计算出
以及
其中 通常为复常数。此外,注意以下恒等式²:
其中 为复数。利用式 (5.34–5.36),我们发现 可简化为一个相对简单的表达式:
其中 由式 (5.15) 定义。之后我们还需要
现在,由式 (5.19) 和 (5.29),我们可以将瞬态振幅重写为
由于物理上有意义的是 的实部,由式 (5.7) 可知,我们关注的是 。为方便起见,我们转而处理如下量:
根据式 (5.39),它满足
这是一个实方程。注意以下关系:
因此,归一化后的瞬态振幅 最终满足一个演化方程,该方程可显式表示为其他动力学变量 、、 和 的函数。
5.2.5 新的运动方程
在此,我们得到了第4.4节中推导出的运动方程(4.57)的“更精确”形式。我们采用相同的方法,再次通过电磁力矩与粘性力矩之间的匹配条件(5.21)来获得运动方程(EOM)。在复数表示下,该条件变为方程(5.24)。如前所述,具有物理意义的是该方程的实部。因此,将 和 代入后,取方程(5.24)的实部,可得:
接下来,在 处取方程(5.7)的实部,得到:
其中使用了方程(4.79)、(5.10)和(5.40)。此外,由方程(4.79)可得:
最后一个等式显然成立,因为:
根据方程(5.48)、(5.7)和(5.18),我们得到:
现在,我们可以像往常一样将方程(5.46)、(5.47)和(5.50)结合起来,得到新的运动方程(EOM):
顺便提一下,为了将 (定义见方程(4.45))表示为其振幅和相位的形式,我们注意到Kelvin函数可以重写为:
其中 、、 和 均为实函数。现在定义:
其中 。此外,令:
最后,我们可以写出
5.2.6 小结
我们推导出了一组新的相位演化方程,它们不再依赖于第 5.2.1 节中提到的四个假设。这些方程为:
以及
第一个方程是我们熟悉的老朋友——“无滑移”约束条件。第二个方程是我们新得到的磁岛角运动方程。注意它与式 (4.57) 的相似性:第一项代表惯性项,第二项对应粘性阻尼力矩,第三项表示电磁力矩,最后一项描述了由于新速度瞬态项的激发所导致的磁岛加速效应。回顾式 (4.57),我们曾通过在惯性项()和粘性项()的极限行为之间进行插值,得到了更简洁的表达式。然而在这里,我们保留了惯性和粘性项的一般形式。最后的方程其实就是式 (5.41),但将 的实部和虚部显式写出,描述了速度瞬态如何因速度和相位的变化而被激发。
本质上,我们已将偏微分方程 (5.1) 转化为一个无限维耦合常微分方程组 (5.60–5.62),这看起来似乎并没有太大改进。然而,我们新得到的常微分方程具有更清晰的物理意义,并且瞬态振幅实际上随 的增大而迅速衰减(这源于式 (5.62) 以及 随 快速增长的事实)。因此,通常只需保留前几个瞬态振幅,即可获得与完整 PDE/ODE 系统(采用有限差分方法)几乎无法区分的结果。
我们引入瞬态项的动机来自于简化相位演化方程与更精确(但计算极其缓慢)的有限差分方法在锁模边界预测上的差异(见第 4.11 节)。事实上,当包含前五个瞬态振幅(即得到一个七维耦合 ODE 系统)时,我们改进后的相位演化方程 (5.60–5.62) 与有限差分方法在锁模边界上的预测结果相差不超过 2%(两种方法预测的模边界在肉眼观察下完全重合)。此外,式 (5.60–5.62) 正确地再现了趋近锁模的过程(如图 4.13 所示)。因此,第 4.11 节中指出的所有问题均可通过引入瞬态振幅得到缓解。
刚刚发展的方法能够非常准确地预测 RFP 中的锁模行为,但相关方程 (5.60–5.62) 比其不含瞬态项的对应形式 (4.56–4.58) 复杂得多。有人可能会觉得我们付出了大量努力却只获得了微小的改进。事实上,
我们的新方法比式 (4.56–4.59) 强大得多,因为它可以很容易地推广式 (5.60–5.62),允许磁岛宽度 、误差场振幅 和误差场相位 随时间变化。这种时间依赖性在模拟磁反馈实验时是必需的,因为在这些实验中,实验者会观察撕裂模在各种可编程误差场波形作用下的振幅(宽度)和相位变化。本章剩余部分将讨论这种情况。
5.3 新的归一化
尽管我们现在允许问题中包含完整的时间依赖性,但我们将告别电阻壁,因为电阻壁会因时变误差场而产生涡流,从而显著增加问题的复杂性。因此,我们有必要调整归一化方式,以消除所有对电阻壁参数(即 和 )的依赖。我们可以通过重新定义归一化的误差场振幅来实现这一点,同时仍保持 和 为 量级:
以及振幅比例因子
为方便起见,我们还将重新定义
注意, 在上一章中的定义略有不同,主要是为了让该章的主要结果——简化的相位演化方程(4.56–4.59)——形式更简洁。其余所有物理量保持不变。归一化的相位演化方程(4.10–4.14)基本保持不变:
其中,
如往常一样,我们假设归一化密度 和粘度 为平直剖面。在本章中,我们还允许误差场以某个可编程的速度旋转,因此相位 满足
其中
为归一化的误差场速度。
5.4 无电阻壳情况下的改进相位演化方程
我们现在将第 5.2 节中描述的方法应用于当前情形。与第 5.2.2 节类似,我们假设速度扰动具有如下形式:
注意,上述方程本质上与方程 (5.7) 相同,仅对第一项做了一些细微修改。具体而言,我们显式地包含了 的依赖关系( 由方程 (5.69) 定义),以便允许归一化模振幅 和误差场振幅 随时间变化。此外, 依赖于 而非 (因为我们现在允许误差场旋转),且不再依赖于 (这种依赖性仅在存在电阻壳时才需要)。另外, 仍是随时间变化的系数,而 的定义与第 5.2.2 节完全相同。即, 是齐次扩散方程 (5.66) 的解,可写为
其中
且 满足
其中 是 的第 个零点。最后,回顾 满足正交条件
将式 (5.72) 代入式 (5.66),我们发现除有理面外的任意位置均有
与之前类似,方程左边最后一项与右边最后一项由于 是齐次方程的解而相互抵消。按照第 5.2.2 节的方法,我们通过选择 使其满足
并选择 使得
其中
在推导式 (5.79) 时,我们使用了正交条件 (5.76)。
为计算 ,我们采用第 5.2 节所述的相同步骤。即首先通过对有理面两侧积分流体运动方程 (5.66)(假设磁岛惯性可忽略)来确定 ,得到
其复数形式为
利用式 (5.72) 和 (4.44),上式变为
其中我们回顾 ,而 由式 (4.45) 给出。但需注意,在式 (4.45) 以及本章其余部分中, 的定义与之前略有不同:
(此前为 )。显然,为使等式 (5.83) 成立,
因此结合式 (4.37) 与 (4.45),我们可以将 表示为
其中 由式 (5.28) 定义。
因此,由式 (5.80),系数 可表示为
当然,此类积分已在第 5.2.4 节中讨论过,其结果为
其中 由式 (5.15) 定义。此外,注意
定义
我们可以结合式 (5.87) 与式 (5.79) 的实部,得到瞬态振幅 的演化方程:
这是一个实方程。
最后,我们以与第 ... 节中详述的完全相同的方式得到运动方程(EOM)。
5.2.5. 粘性力矩与电磁力矩之间的平衡可表示为
此外,与推导方程 (5.47) 和 (5.50) 完全相同的方式,我们可以得到
以及
现在,我们可以像往常一样将方程 (5.92–5.94) 联立,得到新的运动方程(EOM):
5.5 小结
我们推导出了一组新的相位演化方程,适用于误差场的振幅和相速度随时间变化、但不存在电阻壁的情形。这些方程为:
以及
注意,最后一个方程其实就是方程 (5.91),只是将 的实部和虚部显式写出而已。
5.6 磁岛宽度演化
如前所述,在磁反馈实验中,磁岛链的宽度是关注的重点。因此,为了完善我们的方程组 (5.96–5.98),还需加入磁岛宽度演化方程:
回顾一下,磁岛宽度 、误差场强度(度量)、磁流体力学时间尺度 以及粘性扩散时间尺度 分别在方程 (4.1–4.4) 中定义。此外,,,而 和 分别在方程 (3.58) 和 (3.95) 中定义。最后,
其中 由式 (3.26) 定义,且
这与平板情形类似。注意,在上述表达式中我们省略了 上标。将式 (5.99) 与其平板情形的对应式 (2.88) 进行比较,可以看出 起到了熟知的 的作用,而第二项则仅仅是 Thyagaraja 岛饱和项。新的第三项代表了由于有理面上感应的涡流对误差场的响应而对 所做的修正。最后一项由 Fitzpatrick 和 Waelbroeck [40] 得出,表示在磁岛链附近扰动等离子体流动所引起的离子极化电流的致稳效应。
只要扰动速度剖面的局域化尺度远大于磁岛链的宽度,磁岛宽度演化方程 (5.99) 就成立。观察式 (4.39),这一约束条件可转化为 ,其中
而 如前所述,表示饱和磁岛宽度(见式 (2.89))。现在我们引入归一化量:,,,,,,,,
它度量了磁岛链自然旋转周期与磁岛宽度演化时间尺度之比,
它控制磁岛宽度演化方程中外加误差场项的强度,以及
它度量磁岛宽度演化方程中离子极化电流项与误差场项的相对强度。最后,我们可以将式 (5.96–5.99) 重写为如下完整的归一化磁岛演化方程组:
需注意,归一化的误差场振幅 和误差场相速度 是给定的量。
5.7 磁反馈实验
我们现在对三个磁反馈实验进行建模。在每种情况下,我们都对磁岛链施加一个具有不同幅值和相速度波形的共振误差场。需要注意的是,这种误差场更准确地应称为共振磁扰动(Resonant Magnetic Perturbation,简称 RMP),在本节余下部分我们将使用这一术语。由于这类实验主要在托卡马克装置上进行,我们将注意力转向托卡马克平衡态。我们假设归一化电流剖面形式为 ,其中 和 分别是安全因子的中心值和边缘值。我们将研究嵌入该平衡态中的 磁岛链的动力学行为。2,1 有理面的小半径为 。饱和参数 (见式 (5.101))取值为 。此外,我们将理想导体壳移至远离等离子体的位置(),此时 2,1 撕裂模在线性意义上是不稳定的,其稳定性指数为 。所有其他撕裂模在线性意义上都是稳定的。未受扰动时,2,1 岛链的饱和径向宽度为 。参数 (见式 (5.104))取值为 。
5.7.1 RMP 1:瞬态项的重要性
首先考虑等离子体对一个非常简单的 RMP 的响应。具体而言,我们考虑一个静态(即不旋转)的 2,1 RMP,其归一化幅值 缓慢上升,如图 5.1 所示。这种简单的波形足以说明瞬态项在磁岛相位演化中的重要性。如前所述,若忽略瞬态项,扰动速度剖面的包络会瞬时响应磁岛相速度的变化。考虑一个初始处于快速旋转状态的磁岛,在存在一个静止误差场的情况下,我们逐渐增大该误差场的幅值。当误差场幅值达到某一临界值时,磁岛会突然从快速旋转分支跃迁至锁定状态(),此时速度扰动剖面的包络会瞬时从高度局域化(见式 (4.39))转变为高度非局域化(见式 (4.38))。因此,一旦磁岛锁定,扰动速度剖面 会在整个等离子体中发生剧烈变化。当然,如前所述,实际上磁岛锁定事件不应在整个等离子体中瞬时被感知,而应通过粘性扩散从有理面向外传播。
我们采用以下归一化等离子体参数:,,,,对应的 Rutherford 演化时间尺度约为 2,1 岛链自然旋转周期 的 10 倍,而全局粘性弛豫时间尺度约为 。这些参数值是 HBT-EP(高贝塔托卡马克-延长脉冲装置)[30] 等小型托卡马克的典型特征。顺便指出,对于 HBT-EP 这类托卡马克,以非归一化单位计,我们预期 ms。
通过(数值)求解方程 (5.108)、(5.109) 和 (5.111),并使用式 (5.72),我们可以得到在忽略瞬态项()情况下等离子体在两个不同半径处的响应,如图 5.2 所示。实线表示
无瞬态项
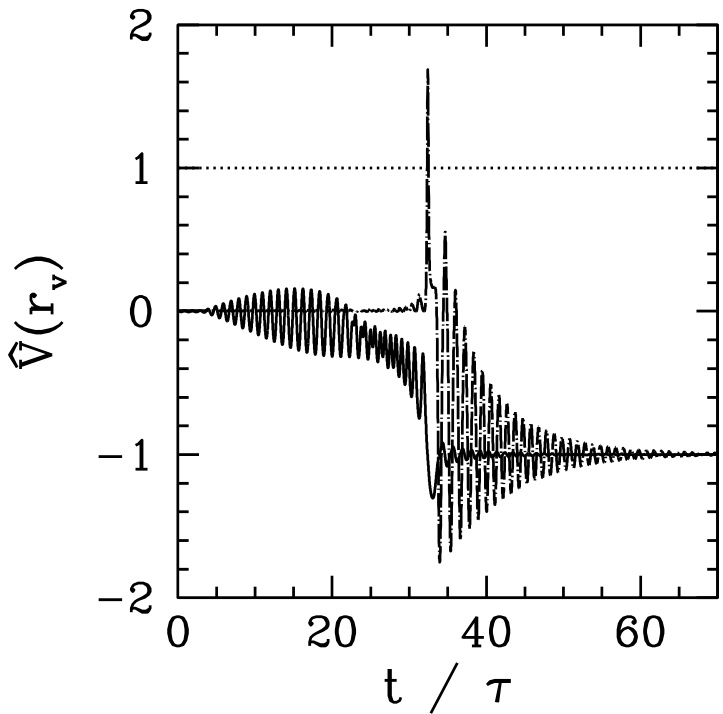
图 5.2:忽略瞬态项时速度扰动的瞬时响应。实线表示在有理面()处计算的速度扰动 ,点划线表示在等离子体内部有理面以内某点()处计算的 。此处参数为 ,,,,。
在有理面(此处位于 )处的速度扰动 ,而点划线表示在等离子体更深处()的速度扰动 。如图所示,一旦磁岛相速度骤降至 (即 ), 处的速度扰动会瞬时发生剧烈的向上跃变。此外,注意磁岛相速度在锁定后会来回“振荡”,并且这种“振荡”在有理面以外的等离子体区域实际上被放大了。这种行为违背了我们的物理预期:即随着远离有理面,磁岛速度的任何振荡都应通过粘性效应而衰减。
包含 5 个瞬态项
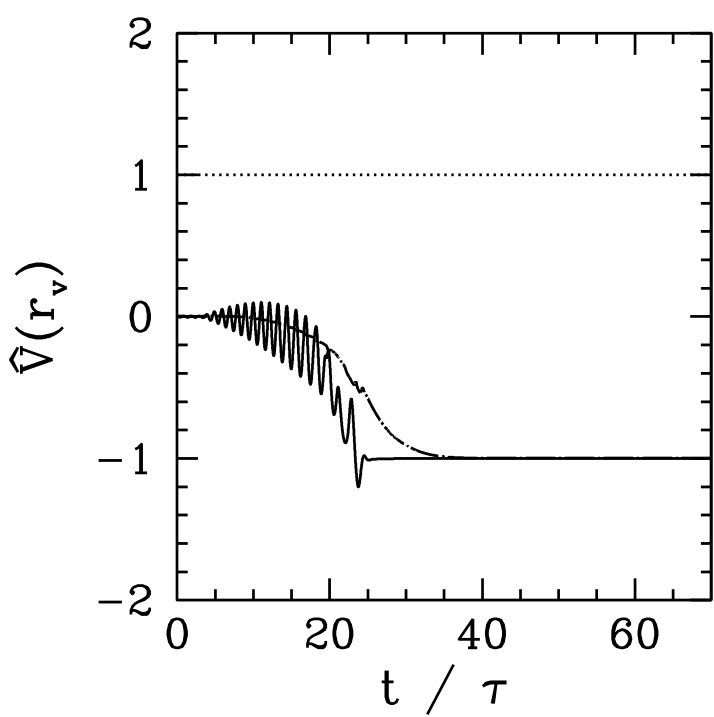
图 5.3:通过引入瞬态项引入时间延迟。实线和点划线仍分别表示在 (有理面)和 处计算的 。所用误差场波形和等离子体参数与图 5.2 相同。
在图 5.3 中,我们求解方程 (5.108–5.111) 并使用式 (5.72),得到在包含瞬态项情况下等离子体对相同误差场波形的响应。除了等离子体更早锁定(即在更低的误差场幅值下锁定,如上一章末尾所述)外,我们还看到,瞬态项的引入使等离子体响应的“尖峰”特性变得平滑。此外,等离子体响应不再出现前述的过度“振荡”,并且随着远离有理面,响应变得更加平滑,这符合物理直觉。最后,正如我们所期望的那样, 处的等离子体并不会与磁岛同时瞬时锁定,而是滞后于磁岛的响应,在显著更晚的时间才锁定。
5.7.2 RMP 2:锁定/解锁行为
我们再次考虑一个静态 RMP,但这次指定一个稍复杂的幅值波形 ,如图 5.4 所示:我们缓慢增大其幅值,保持一段时间恒定,然后缓慢减小。此外,我们使用与之前相同的归一化等离子体参数(,,,)。唯一的区别是我们人为地设 ,以消除离子极化电流对磁岛宽度演化方程的影响。
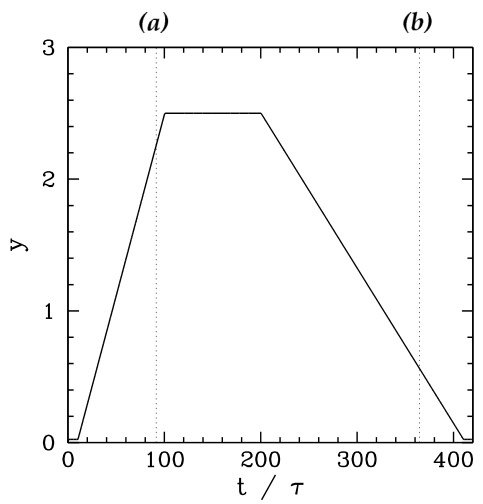
图 5.4:所施加的 2,1 静态共振磁扰动的归一化幅值随时间的变化。
图 5.5 展示了当使用五个瞬态项时,饱和的 2,1 岛链对图 5.4 所示 RMP 的相速度响应。其基本行为现在可能已较为熟悉:即磁岛链在旋转经过扰动时会周期性地加速和减速,但
一旦外部扰动的幅度超过某一阈值,岛链会突然锁定到该外部扰动上。图5.4和图5.5中标记为(a)的时间点即为锁定发生时刻。岛链将保持锁定状态,直到扰动幅度降至第二个阈值以下,此时岛链解锁。图5.4和图5.5中标记为(b)的时间点即为解锁发生时刻。
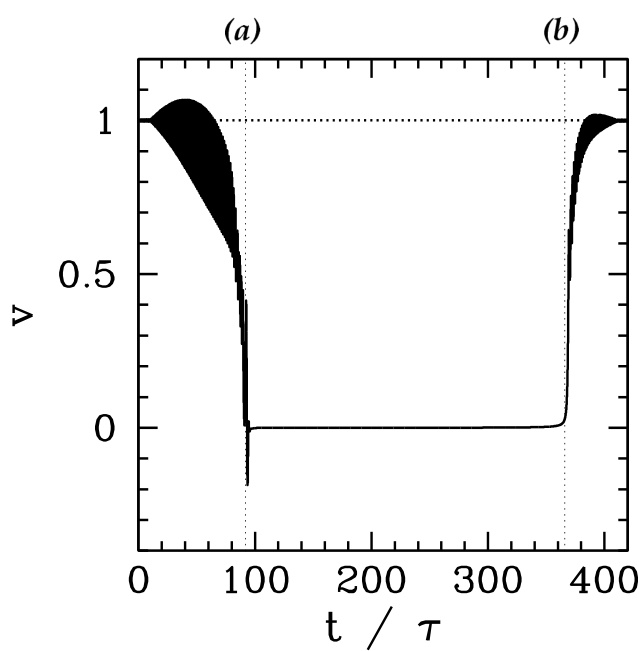
图5.5:在受到图5.4所示的2,1共振磁扰动(RMP)作用下,等离子体中归一化的2,1磁岛相速度随时间的变化。归一化等离子体参数为 。计算中还包含了五个瞬态过程()。
注意,在锁定发生之前,磁岛的平均相速度低于其未受扰动时的值(即 ),这表明振荡的电磁力矩对岛链施加了净制动效应。这一效应在单摆研究中是众所周知的(单摆可粗略描述该动力学行为,参见式(4.70)),其中旋转的平均频率低于自然频率。此外,如第4.7节所述,锁定/解锁循环表现出显著的滞后现象:解锁阈值(对应于时间(b)处的 值)明显小于锁定阈值(对应于时间(a)处的 值)。这种滞后现象已在实验中被观测到 [57]。
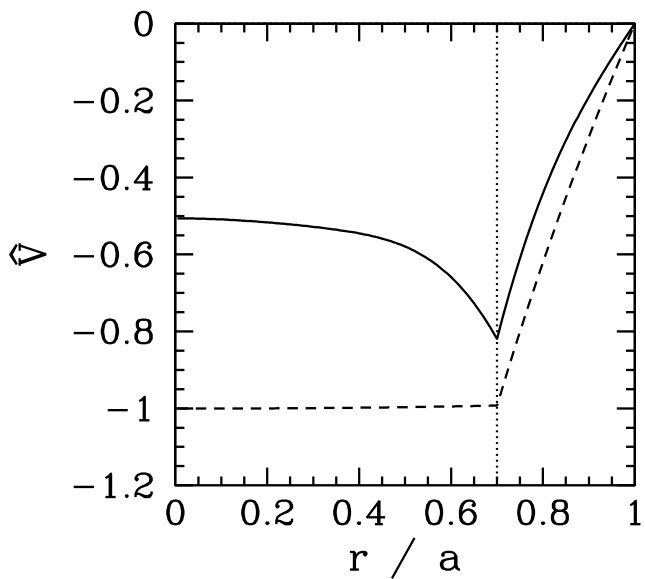
图5.6:在受到图5.4所示的2,1静态RMP作用下,等离子体在即将锁定前(实线)和即将解锁前(虚线)的归一化扰动速度环向角速度剖面。竖直线表示2,1有理面的位置。归一化等离子体参数为 ,且 。
图5.6说明了这种滞后现象的起源。岛链的锁定/解锁行为取决于作用于岛上的电磁力矩与粘性力矩之间的平衡。回顾一下,粘性力矩正比于扰动速度剖面在有理面两侧导数的跃变(见式(4.42))。如图5.6所示,锁定前该跃变要大得多。其原因是:当岛链旋转经过扰动区域时,电磁力矩使其来回振荡,从而驱动出一个未弛豫的速度剖面(见式(4.39))。相反,在岛链解锁前,由于岛链已锁定到静态扰动上,电磁力矩是稳定的,从而驱动出一个弛豫的速度剖面(见式(4.38)),如图5.6所示,该剖面在有理面两侧的导数跃变更小,因此相应的粘性力矩也更小。
正如第4.7节所述,当电磁力矩超过粘性恢复力矩时,岛链锁定到扰动上;而当电磁力矩不足以平衡粘性力矩的拉力时,岛链解锁。由于锁定前的粘性力矩远大于解锁前的粘性力矩,因此锁定所需的电磁力矩(正比于RMP归一化幅度 )远大于解锁所需的电磁力矩。因此,如第4.7节所述,锁定/解锁循环中滞后现象的根源在于:随着速度 的变化,与岛链共同旋转的等离子体区域宽度发生显著变化。
上述讨论说明了准确模拟岛链与等离子体之间粘性耦合的重要性。具体而言,我们需要允许扰动等离子体速度剖面在所施加电磁力矩的作用下粘性演化。如前所述,大多数先前发表的岛演化方程组 [18,54] 假设与岛链共同旋转的等离子体区域具有固定宽度。这类方程在解释实验数据时用途有限,因为它们无法准确模拟锁定/解锁循环中的滞后现象。
图5.7显示了在图5.4所示静态2,1 RMP作用下,2,1磁岛链的归一化宽度随时间的变化。
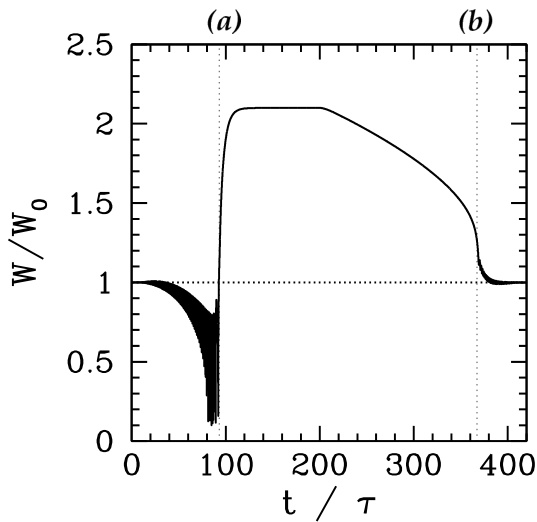
图5.7:在受到图5.4所示2,1静态RMP作用下,2,1磁岛链的归一化宽度随时间的变化。此处 为饱和岛宽。归一化等离子体参数为 ,,,,,且 。
时间演化是在图5.4所示静态2,1 RMP存在的情况下计算的。同样,宽度是通过求解我们的演化方程(5.108–5.111)得到的。注意,我们假设初始时岛已达到饱和宽度(),只要岛未锁定,其宽度在旋转经过扰动区域时就会发生振荡。在此期间,岛的平均宽度被驱动至低于其初始饱和值,因此岛受到净稳定化效应。该效应已在实验 [30,57] 和计算机模拟 [55] 中被观测到,但常被归因于岛宽演化方程(5.111)中离子极化电流项的所谓稳定作用。然而,如前所述,Fitzpatrick 和 Waelbroeck [40,56] 已证明,在电阻/粘性磁流体力学(MHD)框架下,离子极化电流项实际上是起去稳定作用的。事实上,在图5.7的计算中,我们已将离子极化电流设为零(),因此离子极化不可能是图中稳定效应的原因。
实际上,这种“动态稳定化”效应的解释非常简单,其根源在于岛链的非均匀旋转。回顾第4.7节,粗略而言,我们可以将岛/RMP问题类比为一个球在正弦势场 中滚动。球(即岛)在“山丘”区域(例如 )花费的时间比在“山谷”区域(例如 )更长,因为在山丘区域动能更大。然而,“山丘”对应于岛宽演化方程中的稳定相位(即 ,见式(5.111)),而“山谷”对应于去稳定相位(即 )。因此,岛在稳定相位中停留的时间长于在去稳定相位中停留的时间。从图5.7可以看出,当RMP幅度 接近锁定阈值时,这种稳定效应会变得相当显著。
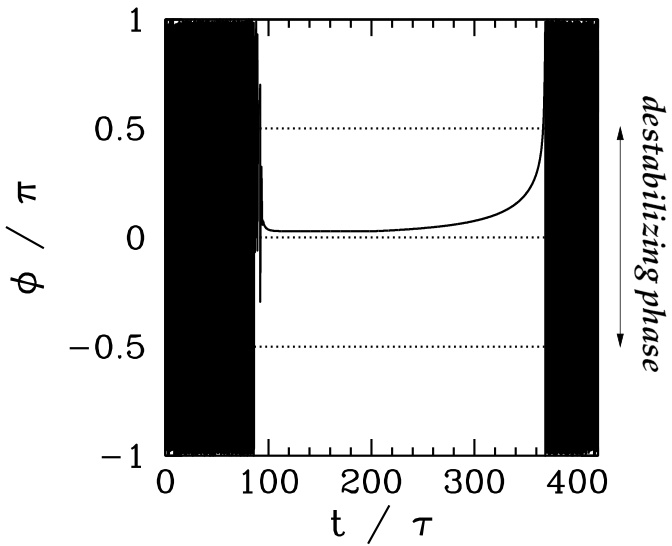
图5.8:在受到图5.4所示2,1静态RMP作用下,2,1磁岛链的螺旋相位随时间的变化。归一化等离子体参数为 ,,,,。
一旦岛锁定到RMP上,它就会被强烈地去稳定化。图5.8显示了岛链螺旋相位随时间的变化。在岛被锁定期间(时间(a)到(b)之间),其相位始终处于相对于扰动的去稳定区域(即 )。这是MHD理论中的一个标准结果 [42],其基本原因在于:一个球无法稳定地停留在山顶(山顶对应于稳定相位)。当扰动幅度逐渐减小、电磁力矩减弱时,粘性恢复力矩会将锁定岛的相位推向稳定区域(即 ),但在到达稳定区域之前,岛就已解锁(回想我们在图4.4中已观察到这一行为)。
由于岛总是以去稳定相位锁定到扰动上,因此撕裂模的磁反馈稳定化只有在防止锁定的情况下才可行。这通常通过以比锁定所需时间尺度更快的速度调制扰动相位来实现 [19]。不幸的是,这种对扰动相位的快速调制几乎肯定需要在真空室内部安装产生磁场的线圈(否则,真空室内的涡流会屏蔽扰动,使其无法作用于等离子体),而这在反应堆环境中是不现实的。
在继续讨论之前,我们指出锁定/解锁循环中滞后现象的另一个来源。电磁力矩正比于归一化扰动幅度 和归一化岛宽 。此外,锁定前的岛宽小于锁定期间的岛宽。因此,锁定岛所需的扰动幅度 比忽略岛宽演化时更大,而解锁所需的 阈值则更小。这一效应加深了锁定/解锁循环中的滞后现象,尽管它并非主要成因。
5.7.3 RMP 3:旋转扰动
对于最终的扰动,我们考虑一个旋转的共振磁扰动(RMP)。在本研究中,我们使用(几乎)与之前相同的等离子体参数(),唯一的区别是我们不再人为地将与 成正比的离子极化电流设为零。为了使 能够取一个不可忽略的值,我们设定 ,此时 (见式 (5.107))。如此小的 值在物理上有些不合理(对应于非常大的饱和磁岛宽度),但我们的目的是观察离子极化电流的影响。事实上,在 HBT-EP 等小型托卡马克装置中,,与我们采用的值相差不大 [5]。
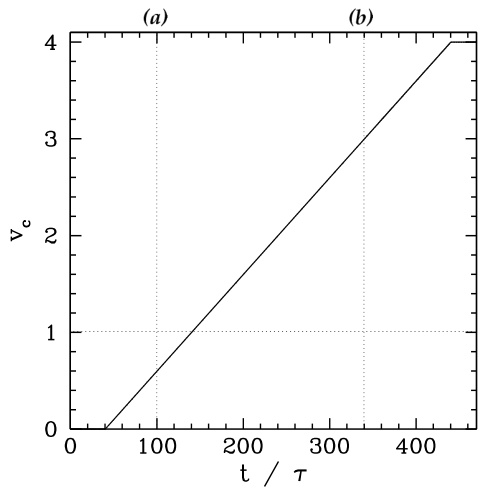
图 5.9:所施加的 2,1 模旋转 RMP 的归一化螺旋相速度随时间的变化。
假设我们将等离子体置于一个 2,1 模旋转 RMP 作用下,其归一化相速度 (见式 (5.71))如图 5.9 所示。可以看出,扰动的旋转频率(即相速度)从零开始线性增加,最终达到 2,1 磁岛链自然频率的四倍。归一化扰动幅度(未显示)在时间 时迅速从零上升,在 处保持恒定,然后在 时迅速下降。
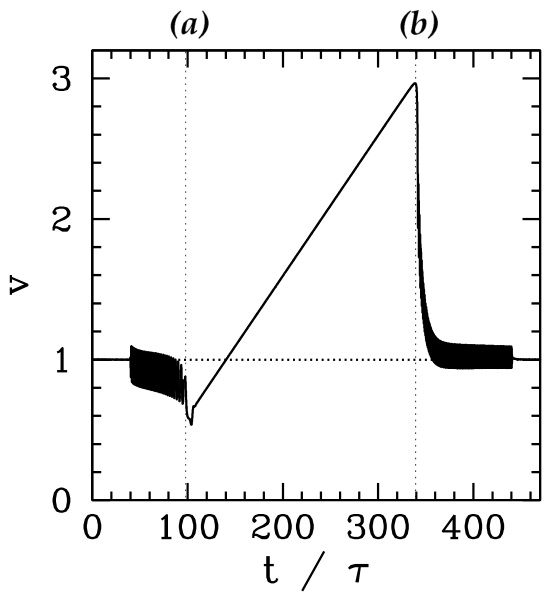
图 5.10:在图 5.9 所示 2,1 模旋转 RMP 作用下,等离子体中 2,1 磁岛归一化相速度随时间的变化。归一化等离子体参数为 ,,,,。此外,。
图 5.10 显示了饱和的 2,1 磁岛链对图 5.9 所示施加的 2,1 模旋转 RMP 的相速度响应。当扰动频率远低于磁岛链的归一化“自然频率”(即 )时,磁岛保持解锁状态,其平均相速度因电磁力矩的净制动效应而被向下驱动,如前一节所述。一旦旋转扰动的频率足够接近磁岛的自然频率,磁岛会突然锁定到扰动上,使得磁岛与扰动的相速度相等。锁定发生在图 5.10 中的时间点 (a)。随后,磁岛相速度被扰动向上扫频,最终达到其自然值的近三倍。然而,一旦扰动相速度与磁岛自然频率之间的差值超过某一阈值,磁岛会突然解锁,其速度迅速减速。解锁发生在图 5.10 中的时间点 (b)。解锁后,磁岛相速度在其自然值略高的水平附近振荡。从图 5.9 可以明显看出,触发锁定所需的外加扰动频率与磁岛自然频率之间的阈值差(绝对值)远小于触发解锁所需的阈值差。这是锁定/解锁循环中滞后现象的另一种表现,源于粘性力矩对磁岛速度的依赖性,如前所述。
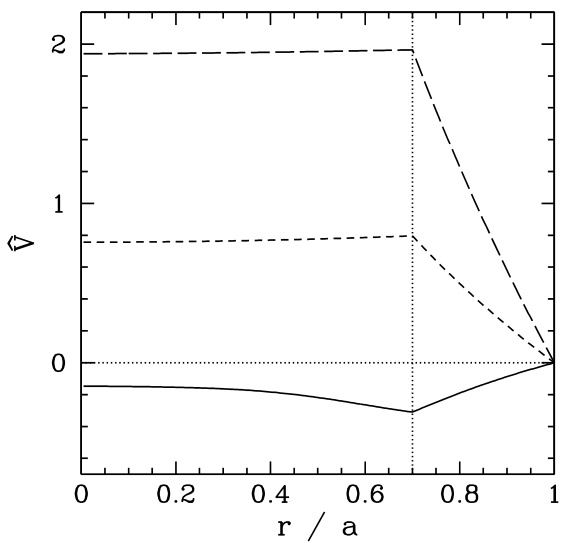
图 5.11:在图 5.9 所示 2,1 模旋转 RMP 作用下,等离子体在锁定前(实线)、锁定与解锁中间时刻(短虚线)以及解锁前(长虚线)的归一化扰动环向角速度剖面。竖直线表示 2,1 有理面的位置。归一化等离子体参数为 ,,,,。
更具体地说,图 5.11 显示了在锁定前、解锁前以及某个中间时刻计算得到的扰动速度剖面。回想一下,当电磁力矩压倒粘性力矩时,磁岛会锁定到扰动上。在锁定前,扰动驱动了一个未弛豫的扰动速度剖面,随着扰动相速度 接近磁岛相速度 ,相应的粘性力矩逐渐减小。当 时,粘性力矩太小,无法平衡电磁力矩,磁岛发生锁定。因此,速度剖面弛豫,粘性力矩进一步减小。由于剖面现已弛豫,我们需要将 推得比 更远,才能使粘性力矩压倒电磁力矩,此时磁岛解锁。
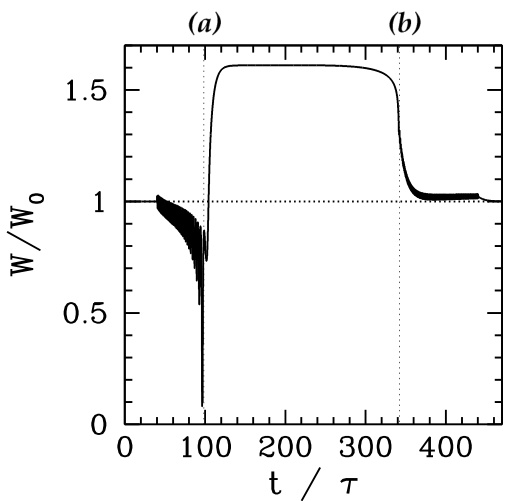
图 5.12:在图 5.9 所示 2,1 模旋转 RMP 作用下,2,1 磁岛链归一化宽度随时间的变化。此处 为饱和磁岛宽度。归一化等离子体参数为 ,,,,。此外,。
图 5.12 显示了在图 5.9 所示 2,1 模旋转 RMP 作用下,2,1 磁岛链的归一化宽度随时间的变化。与之前类似,在锁定前(即时间点 (a) 之前),扰动强烈地稳定磁岛;而在锁定期间(即时间点 (a) 与 (b) 之间),磁岛被扰动去稳定。然而,与之前的情况不同的是,在解锁后(即时间点 (b) 之后),磁岛链被扰动再次去稳定。这一新效应源于离子极化电流的去稳定作用,而之前的计算中并未包含这一项。当磁岛处于解锁状态时,它受到两种不同的“惯性”效应影响。第一种效应是前述的非均匀磁岛旋转,这使得磁岛链在外部扰动的稳定相位中停留更长时间。第二种效应是离子极化电流的去稳定作用。非均匀磁岛旋转的稳定作用在施加扰动与磁岛之间的频率差(绝对值)较小时相对较强,而在频率差较大时较弱(基本上,磁岛旋转得太快,无法“感受到”扰动的影响)[42]。另一方面,离子极化电流的去稳定作用基本上与频率无关(见式 (5.111))。因此,在锁定前(频率差相对较小),前者效应占主导;而在解锁后(频率差相对较大),后者效应占主导。由此可见,上述锁定/解锁循环中的滞后现象,结合刚刚讨论的两种惯性效应的频率依赖性,导致了一种情形:在频率扫描实验中,当扰动使解锁的磁岛链减速时,其受到惯性稳定作用;而当扰动使其加速时,则受到惯性去稳定作用。这一观察结果值得关注,因为它似乎与 HBT-EP 最近的实验结果一致 [5]。
5.8 小结
我们引入了第 4 章推导的相位演化方程的扩展形式,该形式通过瞬态项精确地考虑了磁岛相速度、误差场幅度和误差场相速度的时间变化。利用新的相位演化方程,我们更精确地处理了第 4 章所考虑的问题,即单个撕裂模与电阻壁及外部误差场的相互作用。通过使用包含瞬态项的相位演化方程(5.60–5.62),我们得到了与全 PDE/ODE 相位演化方程(4.75–4.79)高精度(但极其耗时)有限差分积分所预测的锁定边界完全一致的结果。
随后,我们利用瞬态项所提供的新自由度,在问题中加入了磁岛宽度演化和可编程的误差场波形(尽管我们移除了电阻壁),以便模拟磁反馈实验。第一个实验涉及一个非常简单的静态共振磁扰动(RMP),展示了瞬态项在生成物理上合理的扰动速度剖面(即光滑且满足因果律的剖面)中的必要性。第二个实验涉及一个稍复杂的静态 RMP,阐明了扰动速度剖面对磁岛相速度 的强依赖性是锁定/解锁循环中滞后现象的根源。我们还研究了非均匀磁岛旋转对磁岛宽度的去稳定作用(当磁岛锁定时)和稳定作用(当磁岛解锁时)。
最后,我们研究了在频率逐渐向上扫描的旋转 RMP 作用下磁岛的锁定/解锁循环。相关的锁定/解锁循环再次表现出滞后现象(原因同上所述),尽管现在的滞后现象体现在触发锁定和解锁所需的 RMP 频率(即 )与磁岛自然频率(即 )之间差值(绝对值)的不同上。这一最终的 RMP 还展示了当上述频率差较大时,离子极化电流对磁岛宽度演化的重要性。
第 6 章 结论
本论文的目标是推导一组简洁的常微分方程(ODEs),用于描述非线性磁岛链(嵌入在大纵横比、零 、圆形截面的 RFP 等离子体中)在电阻壁和外加共振磁扰动(RMP)作用下的演化行为。我们的研究始于第 3 章,在该章中我们推导了一组由偏微分方程(PDE)和若干 ODE 组成的耦合方程,用于描述磁岛链的相位演化,并具有如下物理特性:随磁岛链一起拖曳的等离子体区域的径向宽度通过粘性作用自洽地确定。
本论文的第一个主要成就是通过合理使用近似方法,将 PDE/ODE 相位演化方程简化为一组简洁的一阶耦合 ODE(见第 4.4 节)。与以往推导的相位演化方程(假设磁岛链共转的等离子体区域宽度固定)不同,我们的新方程组能够精确地模拟磁岛链与等离子体之间的粘性耦合。利用这一简洁的 ODE 相位演化描述,我们研究了磁岛链在电阻壁中涡流产生的制动力矩和静态 RMP 产生的锁定力矩作用下的锁定行为。
误差场。我们的研究得出了一个关于电阻壳对误差场锁模和解锁阈值影响的完整理论,如图4.5所示。
接下来,我们采用有限差分法(见第4.10节)对原始的相位演化偏微分/常微分方程组(PDE/ODE)进行了数值积分,从而发现了我们简化后的ODE相位演化方程中的若干缺陷。具体而言,这两组方程在预测的锁模边界上大致吻合,但并非完全一致。此外,简化相位演化方程所对应的扰动速度剖面会对磁岛链相速度的变化做出瞬时响应,这一点令人不安,因为此类速度变化应通过粘性扩散从有理面逐渐向外传播。
我们的第二项成果是在第5.2节中发展了一套更为完善的相位演化方程,以解决上述问题。尽管该方程组仍仅由ODE构成,但方程本身更为复杂,且所需的动力学变量数量也有所增加,以包含新的类瞬态项。这些新项带来的收益是显著的:它们不仅引入了扰动速度剖面对磁岛链相速度变化作出扩散响应所必需的时间延迟,还能自洽地描述磁岛链宽度的时间演化,以及具有时变幅度和频率的RMP(共振磁扰动)。这类RMP出现在磁反馈实验中,实验者通常施加各种幅度和频率波形的RMP于磁岛链,目的是减小磁岛宽度。因此,我们引入了一个磁岛宽度演化方程(并舍弃了电阻壳,因其感应的涡流对于一般时间依赖的RMP而言过于复杂而难以精确计算),从而与我们的相位演化方程共同构成一个封闭的方程组,完整描述了RMP存在下磁岛链的演化过程。随后,我们在第5.7节中利用该方程组进行了若干示例计算。这些计算的目的既是为了展示在实验相关参数范围内解的典型行为,也是为了帮助实验人员(以及计算机模拟者)解释RMP实验的数据。特别是,我们的方程突显了正确建模磁岛链与等离子体之间粘性耦合的必要性。
在本研究过程中,我们做了一系列简化假设。首先,我们忽略了所有环向效应,这在大纵横比RFP(反场箍缩装置)中实际上并非一个糟糕的假设。具体而言,若我们以纵横比的倒数 对各项进行排序,会发现由于RFP中满足 的排序关系,柱坐标下的曲率项比环向修正项高一个量级 [44]。其次,为简化起见,我们忽略了极向旋转。极向电磁力矩比相应的环向力矩小 倍,但等离子体对极向旋转的转动惯量远小于对环向旋转的转动惯量 [14]。因此,极向力矩对撕裂模频率的修正与环向力矩引起的修正具有相同的量级。需要注意的是,托卡马克中存在强烈的极向流阻尼 [47],但这是环向效应(我们再次强调,在RFP中环向效应远不如柱对称效应重要),因此尚不清楚RFP中的流阻尼是否足够强,以至于可以合理忽略极向力矩。幸运的是,我们可以相当直接地将极向旋转效应纳入模型。
第三,为便于解析处理,我们假设密度和粘度剖面为平直分布,并忽略了有限压强效应 [58]。第四,我们采用了近似的电阻壳色散关系式(3.79),该式未能准确考虑磁岛链相速度的时变特性(见第3.9节)。最后,我们试图通过研究单个代表性撕裂模的动力学来理解slink模的锁模行为。当然,更严格的做法应包含与其他模的非线性耦合,并研究完整slink模的锁模行为。尽管这是一个更为复杂的问题,但显然是可处理的。总之,我们建立了一组简单的耦合一阶ODE方程,用于描述嵌入RFP等离子体中的磁岛链的幅度和相位演化。尽管这些方程是在相当简化的条件下推导得出的,但我们希望它们及其所揭示的物理洞察能对聚变研究界有所裨益。
参考文献
[1] J.A. Wesson, Nucl. Fusion 18, 87 (1978).
[2] R. Carrera, R.D. Hazeltine, and M. Kotschenreuther, Phys. Fluids 29, 899 (1986).
[3] J. Wesson, Tokamaks, (Clarendon Press, Oxford, 1997).
[4] Z. Chang and J.D. Callen, Nucl. Fusion 30, 219 (1990).
[5] R. Fitzpatrick, E. Rossi, and E.P. Yu, Improved evolution equations for magnetic islands in toroidal plasmas subject to externally applied resonant magnetic perturbations, submitted to Phys. Plasmas.
[6] P.H. Rutherford, Phys. Fluids 16, 1903 (1973).
[7] R.B. White, D.A. Monticello, M.N. Rosenbluth, and B.V. Waddell, Phys. Fluids 20, 800 (1977).
[8] A. Thyagaraja, Phys. Fluids 24, 1716 (1981).
[9] H.A.B. Bodin, Nucl. Fusion 30, 1717 (1990).
[10] R.D. Hazeltine and J.D. Meiss, Plasma Confinement, (Addison-Wesley Publishing Company, Redwood City, 1992).
[11] J.B. Taylor, Phys. Rev. Lett. 33, 1139 (1974).
[12] J.B. Taylor, Rev. Mod. Phys. 58, 741 (1986).
[13] J.S. Sarff, N.E. Lanier, S.C. Prager, and M.R. Stoneking, Phys. Rev. Lett. 78, 62 (1997).
[14] R. Fitzpatrick, Phys. Plasmas 6, 1168 (1999).
[15] T. Tamano, W.D. Bard, C. Chu 等, Phys. Rev. Lett. 59, 1444 (1987).
[16] A. Buffa, F. Gnesotto, V. Antoni 等, 见《受控核聚变与等离子体物理》,第21届欧洲会议论文集,蒙彼利埃,1994年(欧洲物理学会,Petit-Lancy,1994年),第1卷,第458页。
[17] T. Bolzonella, S. Ortolani 和 J.S. Sarff, 见《受控核聚变与等离子体物理》,第25届欧洲会议论文集,布拉格,1998年(欧洲物理学会,Petit-Lancy,1998年),第789页。
[18] A.I. Smolyakov, A. Hirose, E. Lazzaro, G.B. Re 和 J.D. Callen, Phys. Plasmas 2, 1581 (1995).
[19] E. Lazzaro 和 M.F.F. Nave, Phys. Fluids 31, 1623 (1988).
[20] G. Bosia 和 E. Lazzaro, Nucl. Fusion 31, 1003 (1990).
[21] G. D'Antonia, IEEE Trans. Nucl. Sci. 41, 216 (1994).
[22] B. Alpher, M.K. Bevir, H.A.B. Bodin 等, Plasma Phys. Controlled Fus. 31, 205 (1989).
[23] A.H. Boozer, Phys. Fluids 24 (1981) 1387.
[24] T.H. Jensen 和 M.S. Chu, J. Plasma Phys. 30 (1983) 57.
[25] M.F.F. Nave 和 J.A. Wesson, Nucl. Fusion 30 (1990), 2575.
[26] R. Fitzpatrick, S.C. Guo, D.J. Den Hartog 和 C.C. Hegna, Phys. Plasmas 6, 3878 (1999).
[27] R. Fitzpatrick 和 E. P. Yu, Phys. Plasmas 7, 3610 (2000).
[28] V.V. Arsenin, L.I. Artemenkov, N.V. Ivanov 等, 见《等离子体物理与受控核聚变研究1978》,第16届国际会议论文集,因斯布鲁克(国际原子能机构,维也纳,1979年),第I卷,第233页。
[29] A.W. Morris, T.C. Hender, J. Hugill 等, Phys. Rev. Lett. 64, 1254 (1990).
[30] G.A. Navratil, C. Cates, M.E. Mael 等, Phys. Plasmas 5, 1855 (1998).
[31] R. Fitzpatrick 和 E. Rossi, Phys. Plasmas 8, 2760 (2001).
[32] H.P. Furth, J. Killeen 和 M.N. Rosenbluth, Phys. Fluids 6, 459 (1963).
[33] W.A. Newcomb, Ann. Phys. 3, 347 (1958).
[34] R. Goldston 和 P.H. Rutherford,《等离子体物理导论》(Institute of Physics Publishing,布里斯托尔,1995年)。
[35] C. Bender 和 S. Orszag,《科学家与工程师的高等数学方法》(McGraw-Hill, Inc.,纽约,1978年)。
[36] B. Coppi、J. Greene 和 J. Johnson,Nuclear Fusion 6, 101 (1966)。
[37] F. Porcelli,Phys. Fluids 30, 1734 (1987)。
[38] M.J. Lighthill,《傅里叶分析与广义函数导论》(剑桥大学出版社,剑桥,1958年)。
[39] D. Biskamp,《非线性磁流体力学》(剑桥大学出版社,剑桥,1993年)。
[40] R. Fitzpatrick 和 F.L. Waelbroeck,Phys. Plasmas 7, 4983 (2000)。
[41] R.B. White,Rev. Mod. Phys. 58, 183 (1986)。
[42] R. Fitzpatrick,Nucl. Fusion 33, 1049 (1993)。
[43] H.K. Moffatt,《导电流体中的磁场产生》(剑桥大学出版社,剑桥,1978年)。
[44] J.P. Freidberg,《理想磁流体力学》(Plenum Press,纽约,1987年)。
[45] V. Antoni、D. Merlin、S. Ortolani 和 R. Paccagnella,Nucl. Fusion 26, 1711 (1986)。
[46] W.A. Newcomb,Ann. Phys. 10, 232 (1960)。
[47] T.H. Stix,Phys. Fluids 16, 1260 (1973)。
[48] R. Fitzpatrick,《利用薄导电壳在磁约束聚变实验中稳定外扭曲模》,德克萨斯大学奥斯汀分校聚变研究所技术报告第731号,1995年。
[49] S.I. Braginskii,载于《等离子体物理评论》,第1卷(M.A. Leontovich 编),Consultants Bureau,纽约(1965年),第205页。
[50] P.H. Rutherford,载于《环形聚变等离子体的基本物理过程》(1985年瓦伦纳课程与研讨会论文集),第2卷,CEC,布鲁塞尔(1986年),第531页。
[51] C.G. Gimblett 和 R.S. Peckover,Proc. R. Soc. Lond. A 368 (1979) 75。
[52] D.A. Gates 和 T.C. Hender,Nucl. Fusion 36 (1996) 273。
[53] R. Fitzpatrick,Phys. Plasmas 5 (1998) 3325。
[54] H. Zohm, A. Kallenbach, H. Bruhns, G. Fussmann, 和 O. Klüber, Europhys. Lett. 11, 745 (1990)。
[55] G. Kurita, T. Tuda, M. Azumi, 和 T. Takeda, Nucl. Fusion 32, 1899 (1992)。
[56] F.L. Waelbroeck 和 R. Fitzpatrick, Phys. Rev. Lett. 78, 1703 (1997)。
[57] T.C. Hender, R. Fitzpatrick, A.W. Morris 等, Nucl. Fusion 32, 2091 (1992)。
[58] M. Kotschenreuther, R.D. Hazeltine, 和 P.J. Morrison, Phys. Fluids 28, 294 (1985)。
个人简历
Edmund Po-ning Yu 于1972年7月26日出生于俄勒冈州科瓦利斯,是 Simon 和 Rachel Yu 的儿子。1980年,他的父亲在佛罗里达大学获得了一份昆虫学(研究虫子)教授的职位,于是全家迁往佛罗里达州盖恩斯维尔的沼泽地带,该地过去曾被称为“猪镇”(Hogtown)。1986年至1990年间,他就读于东区高中(Eastside High School),在那里度过了许多悠闲的留堂时光,并在州举重比赛中获得了第三名。厌倦了南方的生活后,他进入纽约州伊萨卡的康奈尔大学学习电气工程。然而,他觉得物理学更适合自己,因此转到了应用与工程物理学院,并于1994年获得理学学士学位。为了寻找更温暖的气候,他进入德克萨斯大学奥斯汀分校物理系研究生院深造。在短暂而令人谦卑的实验物理经历之后,他有幸于1995年遇到了他的博士导师 Richard Fitzpatrick。1996年底,他又有幸遇到了一位高中同学 Nicole Bodor。
永久地址:3560 NW 30th Blvd
盖恩斯维尔,佛罗里达州 32605
本论文由作者使用 LATEX 排版完成。