数值计算相关论文&书籍中文翻译

21.0 引言

可以肯定地说，用于计算几何公式的计算机运算周期，比用于所有其他用途的总和还要多。这里所说的“计算机”不仅包括名义上的中央处理器（CPU），当然也包括隐藏在计算机图形芯片组中、以及全球各类视频娱乐设备和高清电视盒子中那些往往强大得多的其他 CPU。

• $n$ 维空间中的球体与旋转矩阵
• 关于直线、三角形和多边形的大量内容
• 用于点集的树形数据结构
• 最近邻问题

在本章中，我们将构建一套方法，足以在二维空间中高效地构造 Delaunay 三角剖分，并利用这种三角剖分在非规则网格上对二元函数进行插值，以及其他应用。在实现这一目标（并略作拓展）的过程中，我们还会顺带探讨一些其他有趣且常常有用的主题，包括：

• Voronoi 图及相关内容
• 凸包
• 最小生成树
• 寻找相交对象

等等。

事实上，计算几何及其所嵌入的更广泛的计算机图形学与计算机视觉领域，已成为计算机科学的核心领域，支撑着庞大的工业应用基础，并为各个专业层次的计算机科学家和程序开发者提供了大量就业机会。要在单章篇幅内全面展现这一庞然大物是不可能的。然而，该领域中仍有一些基本技术，应当成为任何从事计算科学研究人员的必备工具。

出于坦诚，我们必须说明：对于上述列表中某些最有趣的话题，我们的讨论将仅限于二维情形，即使三维情形对计算科学同样重要。原因很简单，就是篇幅限制。三维算法通常更为复杂，需要处理更多特殊情况，所得到的代码也往往过长，无法纳入本章。我们已尽力将实用且效率合理的二维代码压缩到适合本章的篇幅。你可以直接将这些代码用于二维问题，也可以从中汲取理解，然后再参考文献去寻找三维解决方案。

另一个需要说明的问题涉及我们对浮点运算的使用，以及对“精确相等”这类特殊情况的处理。由于浮点数及其运算并非精确的，通常从计算角度看，测试精确相等是没有意义的。然而，历史上几何学家总是严格区分，例如一个点是“在三角形内部”、“在边上”还是“在顶点上”。这给该领域带来了一定程度的分裂。一方面（尤其是 1990 年以前），实践者们努力设计使用精确（整数）算术的算法，以优雅地保留这些传统区分；另一方面（尤其是 1990 年以后，随着专用图形处理器中快速浮点运算的普及），许多这类精细区分已不再必要，在追求速度的前提下，可以容忍“机器精度”（machine epsilon）级别的不精确性。在本章中，我们毫不掩饰地站在“不精确”这一阵营。在边界情况下，我们的代码会给出合理的结果，但未必是你所期望的那个特定合理结果。使用者需自行斟酌（Caveat emptor）。

本章另一个不太具体的目标是展现计算几何领域的一些“风味”。这种风味美妙地融合了欧几里得（请原谅！）的元素与现代计算机科学和数学的元素。

以下列出了一些优秀的通用参考文献。

参考文献

de Berg, M., van Kreveld, M., Overmars, M., and Schwarzkopf, O. 2000, Computational Geometry: Algorithms and Applications, 2nd revised ed. (Berlin: Springer). [畅销教材，尤其在引用已发表文献方面非常出色。]

O'Rourke, J. 1998, Computational Geometry in C, 2nd ed. (Cambridge, UK: Cambridge University Press). [文字清晰，解释透彻，并附有 C 语言代码。]

Preparata, F.P. and Shamos, M.I. 1991, Computational Geometry: An Introduction (Berlin: Springer).

Schneider, P.J. and Eberly, D.H. 2003, Geometric Tools for Computer Graphics (San Francisco: Morgan Kaufmann). [包含大量公式与代码的综合性手册。]

Bowyer, A. and Woodwark, J. 1983, A Programmer's Geometry (London: Butterworths). [一本令人愉悦的经典著作，尤其适合看到全大写的 Fortran 代码会怀旧的读者。]

Glassner, A.S., ed. 1990, Graphics Gems (San Diego: Academic Press). [一系列充满实用算法技巧的书籍。]

Arvo, J., ed. 1991, Graphics Gems II (San Diego: Academic Press).

Kirk, D., ed. 1992, Graphics Gems III (Cambridge, MA: Academic Press).

Heckbert, P.S., ed. 1994, Graphics Gems IV (Cambridge, MA: Academic Press).

Euclid, ca. 300BC, Euclid's Elements; reprinted 2002 (Santa Fe, NM: Green Lion Press).

21.1 点与包围盒

一个 $D$ 维空间中的点 $\mathbf{p}$ 由其 $D$ 个笛卡尔坐标 $(x_0,x_1,\dots ,x_{D-1})$ 确定。通常我们只关心 $D=2$（平面上的点）和 $D=3$（三维空间中的点）的情形，但这一概念更具普遍性。

代码中的表示方式正是遵循这一范式。通过避免为各个坐标使用特殊名称（如 $x$、$y$、$z$），我们保留了在 $D$ 维空间中轻松遍历坐标的灵活性。

template<Int DIM> struct Point {
    // 用于表示 DIM 维空间中一个点的简单结构。
    Doub x[DIM];
    Point(const Point &p) {
        for (Int i = 0; i < DIM; i++) x[i] = p.x[i];
    }
    Point& operator= (const Point &p) {
        for (Int i = 0; i < DIM; i++) x[i] = p.x[i];
        return *this;
    }
    bool operator== (const Point &p) const {
        for (Int i = 0; i < DIM; i++) if (x[i] != p.x[i]) return false;
        return true;
    }
    Point(Doub x0 = 0.0, Doub x1 = 0.0, Doub x2 = 0.0) {
        x[0] = x0;
        if (DIM > 1) x[1] = x1;
        if (DIM > 2) x[2] = x2;
        // 更高维的初始化可以省略。
        if (DIM > 3) throw("Point not implemented for DIM > 3");
    }
};

为了代码简洁，上述构造函数可能会传递一些不必要的零值默认参数。如果你在意这一点，可以轻松地进行清理。

给定两个点 $\mathbf{p}$ 和 $\mathbf{q}$，我们可以计算它们之间的距离 $d$：

$$d=|\mathbf{p}-\mathbf{q}|={\left[\sum _{i=0}^{D-1}(p_i-q_i{)}^2\right]}^{1/2}$$

其中 $p_i$ 和 $q_i$ 分别是每个点的笛卡尔坐标。

在代码中，我们有：

template<Int DIM> Doub dist(const Point<DIM> &p, const Point<DIM> &q) {
    // 返回 DIM 维空间中两点之间的距离。
    Doub dd = 0.0;
    for (Int j = 0; j < DIM; j++) dd += SQR(q.x[j] - p.x[j]);
    return sqrt(dd);
}

注意，dist 并不是 Point 类的成员函数，而是一个独立的函数，其参数为 Point 类型。我们还将对 dist 进行重载，以支持其他类型的参数，表示不同对象之间的其他类型距离。

21.1.1 盒子（Boxes）

所谓一个 盒子（box），是指与坐标轴对齐的矩形（当 $D=2$ 时）或长方体（当 $D=3$ 时，也称为“砖块”）。盒子之所以有趣，是因为它们可以对 $D$ 维空间进行密铺（即划分），并且可以包含其他对象。事实上，每个有限的、有延展性的对象都有一个包围盒（bounding box），即唯一能包含该对象的最小盒子。

表示一个盒子的一种方法是使用两个特殊的、对角相对的角点。第一个点（“low”）的坐标值是盒子表面上各坐标的最小值；第二个点（“high”）的坐标值是各坐标的最大值。显然，盒子的其他所有角点在每一维上的坐标值要么等于“low”的对应值，要么等于“high”的对应值；所有这些组合共构成 $2^D$ 个角点。

代码实现如下：

pointbox.h

template<Int DIM> struct Box {
    // 用于表示 DIM 维笛卡尔盒子的结构。
    Point<DIM> lo, hi;
    // 存储两个对角相对的角点（所有坐标的最小值和最大值）。
    Box() {}
    Box(const Point<DIM> &mylo, const Point<DIM> &myhi) : lo(mylo), hi(myhi) {}
};

注意，这里不需要显式定义拷贝构造函数和赋值运算符，因为默认情况下两个 Point 成员会被正确地拷贝或赋值（这是该表示方式的一个便利之处）。

一个点可能位于盒子外部、内部，或者——理论上——位于其表面上。如 §21.0 中所述，我们使用（近似的）浮点数而非（精确的）整数来表示所有坐标，因此依赖坐标值或距离的精确相等是不明智的。因此，我们将谨慎对待盒子表面的精确概念；通常，若恰好出现某种精确相等的情况，我们会将表面视为盒子内部的一部分。

若一个点位于盒子外部，则定义该点到盒子的距离为到盒子表面（或内部）最近点的距离。观察图 21.1.1 可知，该距离是该点到某些（但非全部）界定盒子的超平面的距离的毕达哥拉斯和（即平方和的平方根）。规则如下：当某点的某一坐标大于盒子对应坐标的最大值，或小于最小值时，该坐标对距离平方和有贡献；当该点的坐标介于最大值和最小值之间时，则不对距离平方和产生贡献，因为（沿该坐标方向）最短路径可垂直于超平面。若点位于盒子内部或表面上，则定义其到盒子的距离为零。

上述距离定义体现在以下代码中：

template<Int DIM> Doub dist(const Box<DIM> &b, const Point<DIM> &p) {
    // 若点 p 位于盒子 b 外部，则返回到 b 上最近点的距离；
    // 若 p 在 b 内部或表面上，则返回零。
    Doub dd = 0;
    for (Int i = 0; i < DIM; i++) {
        if (p.x[i] < b.lo.x[i]) dd += SQR(p.x[i] - b.lo.x[i]);
        if (p.x[i] > b.hi.x[i]) dd += SQR(p.x[i] - b.hi.x[i]);
    }
    return sqrt(dd);
}

我们经常需要判断一个点是在盒子内部还是外部。上述 dist 函数可用于此目的：返回正值表示在外部，返回零表示在内部。

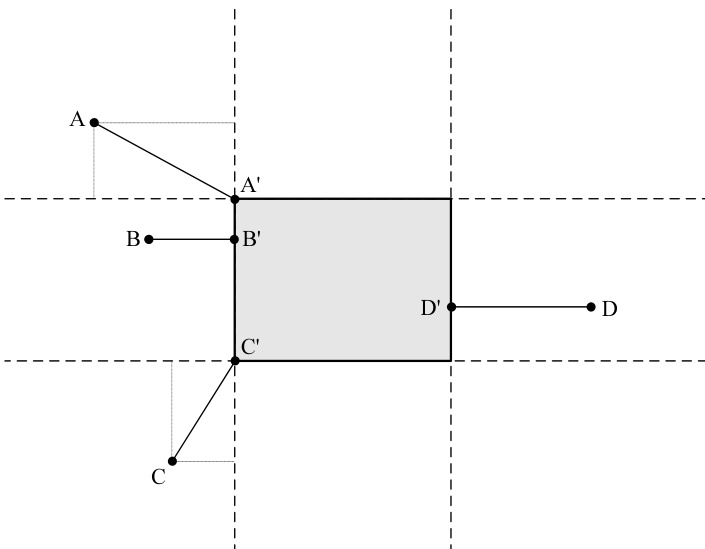
图 21.1. 点到 $D$ 维盒子的距离。通用公式（如线段 $A{A}^{\prime }$ 和 $C{C}^{\prime }$ 所示）是到包含盒子较近一侧的平面的 $D$ 个距离的毕达哥拉斯和。但当点位于两个这样的平行平面之间时（如 $B{B}^{\prime }$ 和 $D{D}^{\prime }$ 所示），对应的坐标不计入求和。

若你只关心点在内部还是外部，而不关心具体距离，则可对代码进行优化：将 dd 替换为布尔变量，用逻辑或（logical-or）代替加法，并省略平方根运算。其余逻辑保持不变。

21.1.2 盒子二叉树的节点

下一节中，我们将构建一个嵌套盒子的二叉树，其中每个盒子被细分为两个子盒子并与之关联。树中的每个盒子还将包含一个位于该盒子内部的点列表。为此，我们在此给出一个从 Box 结构派生的结构，它增加了若干变量，用于指向父盒子、两个子盒子，以及点列表中的起始和结束索引（标识盒子内点的范围）。构造函数显式地设置所有这些值。

template<Int DIM> struct Boxnode : Box<DIM> {
    // 包含点的盒子二叉树中的节点。详见正文说明。
    Int mom, dau1, dau2, ptlo, pthi;
    Boxnode() {}
    Boxnode(Point<DIM> mylo, Point<DIM> myhi, Int mymom, Int myd1,
            Int myd2, Int myptlo, Int mypthi) :
        Box<DIM>(mylo, myhi), mom(mymom), dau1(myd1), dau2(myd2),
        ptlo(myptlo), pthi(mypthi) {}
};

21.2 KD 树与最近邻查找

很久以前，“kd 树”（或 “k-D 树”）是 “k 维树（k-dimensional tree）” 的缩写。然而，该术语如今特指一种非常具体且实用的树结构，用于对点集进行划分，尤其适用于低维空间（如 2 维或 3 维）。包含 $N$ 个点的 KD 树可在 $O(N\log N)$ 时间和 $O(N)$ 空间内构建。构建完成后，KD 树可高效支持多种操作，例如在 $O(\log N)$ 时间内找到某点的最近邻，或在 $O(N\log N)$ 时间内找到所有点的最近邻。KD 树最早由 Bentley [8] 于 1975 年提出。下面我们来看其工作原理。

从一个非常大的盒子开始，这个盒子要能轻松包含所有感兴趣的点。将这个根盒子设得极其巨大没有任何惩罚，因此坐标取 $\pm 10^{99}$ 是完全可以接受的。现在，在根盒子内部生成一个包含 $N$ 个点（对你的应用而言感兴趣的点）的列表。KD 树的定义原则如下：

• 盒子被连续地划分为两个子盒子。
• 每次划分都沿着某一坐标轴进行。
• 在连续的划分中，坐标轴按循环顺序依次使用。
• 在进行划分时，“切割”位置的选择应使得两侧的点数相等（若点数为奇数，则两侧点数相差 1）。

在这些原则下，仍有一些任意的设计选择需要确定。在下面的实现中，划分的“切割”线恰好穿过其中一个点（即共享该点的某个坐标值）。这样可以避免其他选择可能带来的额外簿记开销。此外，当一个盒子节点包含一个或两个点时，我们就终止树的构建，不再将包含两个点的盒子进一步划分为两个单点盒子。这种选择很自然，因为 Boxnode 结构已经包含指向两个点的指针（ptlo 和 pthi），并且这样做最多可将存储的盒子总数减少 50%。

牢记这些原则和设计规则，你就可以理解图 21.2.1，它展示了一个包含 1000 个点的二维 KD 树。（作为一点艺术上的自由处理，图中的根盒子已被缩小到刚好包含所有点，而不是延伸到无穷远处。）

有趣的是，给定点数 $N$，我们可以给出一个精确的公式来计算 KD 树划分规则所产生的盒子数量。（这使得树的内存分配变得非常直接。）设 $N_B(N)$ 为 $N$ 个点所需的盒子数量，则以下两个显然的递推关系描述了初始划分的情形：将 $2n$ 个点划分为 $n$ 和 $n$，或将 $2n-1$ 个点划分为 $n$ 和 $n-1$：

$$\begin{array}{r}{N}_B(2n)=2N_B(n)+1\\ N_B(2n-1)=N_B(n)+N_B(n-1)+1\end{array}$$

两个公式中的 +1 都是指在每个阶段将两个子树“粘合”在一起的母盒子。这些递推关系的解为：

$$N_B(N)=\min (M-1,2N-\frac{1}{7}M-1)$$

其中 $M$ 是大于或等于 $N$ 的最小 2 的幂，即：

$$M=2^{\lceil {\log }_{2}N\rceil }$$

（你可以通过归纳法验证这个解，考虑 min 函数的各种情况。或者——更有趣的是——你可以编写一个程序，在 $N<10^9$ 的范围内数值验证它。）

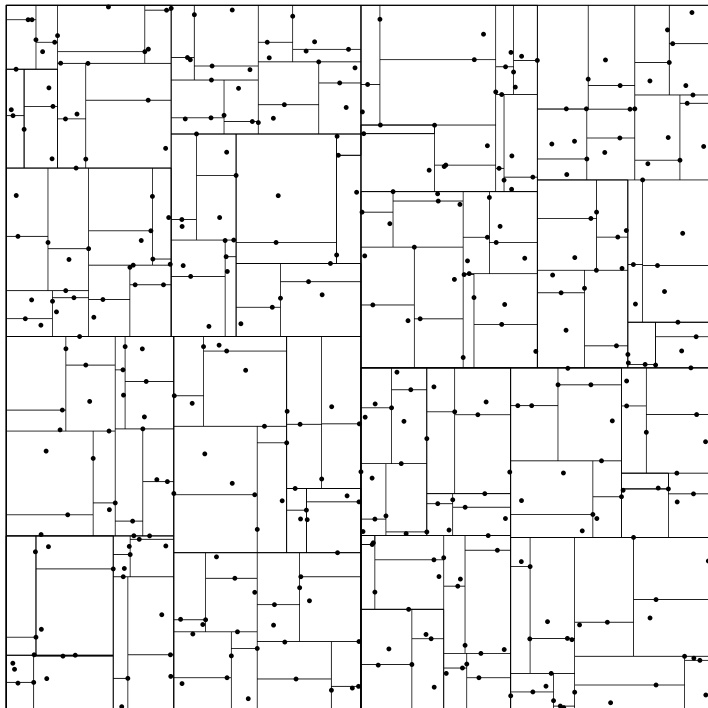
图 21.2.1. 由平面上 1000 个点构建的 KD 树。图中可见第一次划分是一条贯穿整个高度的垂直线，位于图的中间位置。接下来的划分是水平线，延伸至图的一半宽度。划分在水平和垂直方向交替进行，并在每个阶段将点划分为（几乎）相等的数量。当一个盒子中只剩一个或两个点时（其中一个通常位于盒子边界上），树的构建终止。

21.2.1 KD 树的实现

我们将 KD 树实现为一个结构体，它从一个 Point 向量构建而成，并包含一些方法，用于实现我们将在下文讨论的主要应用，主要是各种最近邻问题。

template<Int DIM> struct KDtree {
    // 用于实现 KD 树的结构体。
    static const Doub BIG;
    Int nboxes, npts;
    vector <Point<DIM> > &ptss;
    Boxnode<DIM> *boxes;
    VecInt ptIdx, rptIdx;
    Doub *coordinates;
    KDtree(vector< Point<DIM> > &pts);
    ~KDtree() { delete [] boxes; }
    // 接下来是树构建完成后使用的工具函数。见下文。
    Doub dist(Int jpt, Int kpt);
    Int locate(Point<DIM> pt);
    Int locate(Int jpt);
    // 接下来是使用 KD 树的应用。见正文。
    Int nearest(Int jpt);
    Int nearest(Point<DIM> pt);
    void nearest(Int jpt, Int *nn, Doub *dn, Int n);
    static void sift_down(Doub *heap, Int *ndx, Int nn);
    Int locatenear(Point<DIM> pt, Doub r, Int *list, Int nmax);
};

template<Int DIM> const Doub KDtree<DIM>::BIG(1.0e99);

注意，KDtree 结构体保留了对其创建所用 Point 向量的引用。这在某些应用中会被使用，同时也意味着用户在 KD 树的作用域内不应修改该点向量。数组 coordinates 是点向量在 KD 树构建过程中的内部表示，构建完成后会立即释放回内存池。

KD 树之所以能快速构建，是因为存在时间复杂度为 $O(N)$ 的快速划分算法，这些算法不仅能在一个包含 $N$ 个值的数组中找到中位数值，还能将所有较小的值移到数组一侧，所有较大的值移到另一侧。我们在 §8.5 的 select 例程中已经见过这样的算法。这里我们需要一个稍作修改的变体 selecti，它不是根据整数数组自身的值进行划分，而是利用这些整数作为索引去访问另一个保持不变的值数组。由于我们需要对数组的子段进行划分，因此我们通过地址传递所有数组引用。

Int selecti(const Int k, Int *index, Int n, Doub *arr)
// 对 index[0..n-1] 进行排列，使得 arr[index[0..k-1]] ≤ arr[index[k]] ≤ arr[index[k+1..n-1]]。
// 数组 arr 不会被修改。参见 select 例程中的注释。
{
    Int i, ia, ir, j, l, mid;
    Doub a;
    l = 0;
    ir = n - 1;
    for (;;) {
        if (ir <= l + 1) {
            if (ir == l + 1 && arr[index[ir]] < arr[index[l]]) SWAP(index[l], index[ir]);
            SWAP(index[k], index[l]);
            return index[k];
        } else {
            mid = (l + ir) >> 1;
            SWAP(index[mid], index[l + 1]);
            if (arr[index[l]] > arr[index[ir]]) SWAP(index[l], index[ir]);
            if (arr[index[l + 1]] > arr[index[ir]]) SWAP(index[l + 1], index[ir]);
            if (arr[index[l]] > arr[index[l + 1]]) SWAP(index[l], index[l + 1]);
            i = l + 1;
            j = ir;
            ia = index[l + 1];
            a = arr[ia];
            for (;;) {
                do i++; while (arr[index[i]] < a);
                do j--; while (arr[index[j]] > a);
                if (j < i) break;
                SWAP(index[i], index[j]);
            }
            index[l + 1] = index[j];
            index[j] = ia;
            if (j >= k) ir = j - 1;
            if (j <= k) l = i;
        }
    }
}

构建 KD 树的基本策略如下：首先设置一个整数数组，用于索引 $N$ 个点（下文中的 ptindex）。接着，将所有点的坐标复制到一个数组（coordinates）中，其中所有 $x_0$ 坐标连续存放，接着是所有 $x_1$ 坐标，依此类推，直到所有维度。然后使用 selecti 根据点的 $x_0$ 坐标值对点索引进行划分（并重排），使得划分两侧各有半数的点。这两个子数组现在分别对应两个新的子盒子。接着，再根据 $x_1$ 坐标值对每个子数组进行划分。如此循环递归地进行下去，坐标轴按循环顺序依次使用。

这种递归非常简单，可以很容易地编码为一个简单的“待处理任务列表”，从而避免递归函数调用的开销。一个待处理任务包括一个指向待进一步划分的盒子的索引（可以看作是“待产母亲”），以及一个记录下一次应沿哪个维度进行划分的值。由于树是“深度优先”构建的，任务列表的大小永远不会超过盒子总数的对数。每个新生成的子盒子都带有指向其母盒子的指针，以及指向点索引数组 ptindex 中起始和结束元素的指针。尽管这些元素在后续划分中通常会被重新排列，但它们永远不会被移出子盒子首次创建时指定的范围。这就是为什么整个过程可以在单个点索引数组中完成，所有盒子只需指向该数组的某个子范围即可。

下面的 KDtree 构造函数现在应该很容易理解了。

template<Int DIM> KDtree<DIM>::KDtree(vector< Point<DIM> > &pts) : ptss(pts), npts(pts.size()), ptindex(npts), rptindex(npts) {
    // 从点向量构建 KD 树。
    Int ntmp, m, k, kk, j, nowtask, jbox, tmom, tdim, ptlo, pthi, np;
    Int *hp;
    Doub *cp;
    Int taskmom[50], taskdim[50];
    for (k = 0; k < npts; k++) ptindex[k] = k; // 初始化点索引。
    // 计算盒子数量并分配内存。
    m = 1;
    for (ntmp = npts; ntmp; ntmp >>= 1) {
        m <<= 1;
    }
    nboxes = 2 * npts - (m >> 1);
    if (m < nboxes) nboxes = m;
    nboxes--;
    boxes = new Boxnode<DIM>[nboxes];
    // 将点坐标复制到连续数组中。
    coordinates = new Doub[DIM * npts];
    for (j = 0, kk = 0; j < DIM; j++, kk += npts) {
        for (k = 0; k < npts; k++) coordinates[kk + k] = pts[k].x[j];
    }
    // 初始化根盒子并将其加入任务列表以进行细分。
    Point<DIM> lo(-BIG, -BIG, -BIG), hi(BIG, BIG, BIG); // 语法对 2-D 也适用。
    boxes[0] = Boxnode<DIM>(lo, hi, 0, 0, 0, 0, npts - 1);
    jbox = 0;
    taskmom[1] = 0;
    taskdim[1] = 0;
    nowtask = 1;
    while (nowtask) {
        tmom = taskmom[nowtask];
        tdim = taskdim[nowtask--];
        ptlo = boxes[tmom].ptlo;
        pthi = boxes[tmom].pthi;
        hp = &ptindex[ptlo];
        cp = &coordinates[tdim * npts];
        np = pthi - ptlo + 1;
        kk = (np - 1) / 2;
        (void) selecti(kk, hp, np, cp);
        // 现在创建子盒子，如果需要进一步细分，则将其推入任务列表。
        // kk 是左侧最后一个点的索引（边界点）。
        Point<DIM> hi = boxes[tmom].hi;
        Point<DIM> lo = boxes[tmom].lo;
        Doub cut = coordinates[tdim * npts + hp[kk]];
        hi.x[tdim] = cut;
        lo.x[tdim] = cut;
        boxes[++jbox] = Boxnode<DIM>(boxes[tmom].lo, hi, tmom, 0, 0, ptlo, ptlo + kk);
        boxes[++jbox] = Boxnode<DIM>(lo, boxes[tmom].hi, tmom, 0, 0, ptlo + kk + 1, pthi);
        boxes[tmom].dau1 = jbox - 1;
        boxes[tmom].dau2 = jbox;
        if (kk > 1) {
            taskmom[++nowtask] = jbox - 1;
            taskdim[nowtask] = (tdim + 1) % DIM;
        }
        if (np - kk - 1 > 1) {
            taskmom[++nowtask] = jbox;
            taskdim[nowtask] = (tdim + 1) % DIM;
        }
    }
    for (j = 0; j < npts; j++) rptindex[ptindex[j]] = j; // 创建反向索引。
    delete [] coordinates; // 不再需要它们了。
}

提供一些简单的工具函数也很容易。尽管我们通常更倾向于让距离（dist）函数作为独立函数存在，但拥有一个 KDtree 成员函数来返回 KD 树中两个点之间的距离（通过它们在底层点向量中的整数位置引用）也是非常有用的。

template<Int DIM> Doub KDtree<DIM>::disti(Int jpt, Int kpt) {
    // 返回kdtree中两个点之间的距离（通过它们在点数组中的索引指定），
    // 但如果两点相同，则返回一个很大的值。
    if (jpt == kpt) return BIG;
    else return dist(ptss[jpt], ptss[kpt]);
}

当两点相同时返回BIG有一个特殊原因：稍后当我们寻找某一点的最近邻时，我们不希望答案总是“它自己！”

另一个简单的函数以任意Point作为参数，并返回唯一包含该点的盒子的索引。在此函数中，我们首次看到如何层次化地遍历树：从根盒子开始，在每一层只选择两个子盒子中的一个。此外，通过跟踪下一次要分割的维度（下面的jdim），我们在每一层只需检查该点的一个坐标。显然，整个过程的时间复杂度为 $O(\log N)$，因为树的层数最多只有这么多。

template<Int DIM> Int KDtree<DIM>::locate(Point<DIM> pt) {
    // 给定任意点pt，返回其所在的kdtree盒子的索引。
    Int nb, d1, jdim;
    nb = jdim = 0;
    while (boxes[nb].dau1) {
        d1 = boxes[nb].dau1;
        if (pt.x[jdim] <= boxes[d1].hi.x[jdim]) nb = d1;
        else nb = boxes[nb].dau2;
        jdim = ++jdim % DIM;
    }
    return nb;
}

可以通过返回的整数（例如j）从KDtree中获取实际的Box，方法是引用boxes[j]，因为Boxnode是Box的派生类。

另一个非常类似的工具函数返回包含用于构建KD树的某个点的盒子索引。由于坐标值可能存在多个相等的情况（此时一些相等的点可能位于中位数分割的一侧，而另一些位于另一侧），因此该盒子不一定与上述例程返回的盒子相同。

template<Int DIM> Int KDtree<DIM>::locate(Int jpt) {
    // 给定kdtree中某点的索引，返回其所在盒子的索引。
    Int nb, d1, jh;
    jh = rptindex[jpt];
    nb = 0;
    while (boxes[nb].dau1) {
        d1 = boxes[nb].dau1;
        if (jh <= boxes[d1].pthi) nb = d1;
        else nb = boxes[nb].dau2;
    }
    return nb;
}

21.2.2 KD树的应用

KD树的大多数应用都利用了其嵌套盒子的局部性特性。通过几个例子可以最好地理解这一点。

假设我们想知道KD树中的 $N$ 个点中哪一个离任意点 $\mathbf{p}$（不一定是树中的点）最近。如果没有树结构，显然需要 $O(N)$ 次操作，因为我们必须依次将 $\mathbf{p}$ 与每个候选点进行比较。然而，如果我们已经投入了 $O(N\log N)$ 次操作来构建树，那么可以按以下方式处理：首先，找到 $\mathbf{p}$ 所在的盒子，并找到该盒子中树内离 $\mathbf{p}$ 最近的点。如上所述，这需要 $O(\log N)$ 次操作。找到的点实际上可能是最近邻（我们尚不确定），但无论如何，其距离现在给出了真实最近邻可能距离的上界。

其次，通过深度优先递归遍历树（与构建树时完全相同的方式）。当我们遇到每个新盒子时，检查它是否可能包含比目前已找到的最近点更近的点。由于我们从一个已经相当近的点开始（与 $\mathbf{p}$ 在同一盒子中），大多数盒子在此步骤中会被拒绝。当一个盒子被拒绝时，我们无需打开其子盒子，因此树的整个分支会被“剪枝”。平均而言，只有大约 $O(\log N)$ 个盒子会被实际打开，因此查找最近点的总工作量为 $O(\log N)$。

如果我们只对单个点 $\mathbf{p}$ 感兴趣，那么“慢速”的 $O(N)$ 方法会更快。但如果我们对许多不同的点 ${\mathbf{p}}_i$ 重复此操作，每次都与树中相同的 $N$ 个点进行比较，那么依次对每个 ${\mathbf{p}}_i$ 调用以下例程将带来巨大优势。

template<Int DIM> Int KDtree<DIM>::nearest(Point<DIM> pt) {
    // 给定任意位置pt，返回kdtree中最近点的索引。
    Int i, k, nrst, ntask;
    Int task[50];
    Doub dnrst = BIG, d;
    // 第一阶段：找到与pt在同一盒子中的最近kdtree点。
    k = locate(pt); // pt位于哪个盒子？
    for (i = boxes[k].ptlo; i <= boxes[k].pthi; i++) { // 寻找最近点。
        d = dist(ptss[ptindex[i]], pt);
        if (d < dnrst) {
            nrst = ptindex[i];
            dnrst = d;
        }
    }
    // 第二阶段：遍历树，仅打开可能包含更近点的盒子。
    task[1] = 0;
    ntask = 1;
    while (ntask) {
        k = task[ntask--];
        if (dist_box[k].pt < dnrst) {
            if (boxes[k].dau1) {
                task[++ntask] = boxes[k].dau1;
                task[++ntask] = boxes[k].dau2;
            } else {
                for (i = boxes[k].ptlo; i <= boxes[k].pthi; i++) {
                    d = dist(ptss[ptindex[i]], pt);
                    if (d < dnrst) {
                        nrst = ptindex[i];
                        dnrst = d;
                    }
                }
            }
        }
    }
    return nrst;
}

如果我们想知道的不是任意位置的最近邻点，而是KD树中存储的某个点的最近邻点呢？上述例程无法胜任。如果我们传入树中的一个点，它会给出显而易见的结果：该点是它自己的最近邻！我们需要修改该例程，使用KDtree中的disti函数，该函数将点到自身的距离定义为很大而非很小。

另一个有用的功能是不仅找到单个最近邻，而是找到指定数量 $n<N-1$ 的最近邻。这里的技巧是避免使算法复杂度变为 $O(n\log N)$（如果对每个候选点都与当前找到的 $n$ 个最佳点逐一比较，就会出现这种情况）。一种有效的方法是使用堆结构，如§8.3所述，并在§8.5的hpsel例程中（用于非常类似的目的）使用过。此时工作量按 $O(\log n\log N)$ 缩放。

以下例程的编码方式确保在 $n=1$（查找单个最近邻）的情况下几乎不会损失效率，而在 $n>1$ 时使用堆结构。

template<Int DIM> void KDtree<DIM>::nearest(Int jpt, Int *nn, Doub *dn, Int n) {
    // 给定kdtree中某点的索引jpt，返回树中离该点最近的n个点的索引列表nn[0..n-1]，
    // 以及它们的距离列表dn[0..n-1]。
    Int i, k, ntask, kp;
    Int task[50];
    Doub d;
    if (n > npts - 1) throw("too many neighbors requested");
    for (i = 0; i < n; i++) dn[i] = BIG;
    // 找到包含足够点数的最小母盒子以初始化堆。
    kp = boxes[locate(jpt)].mom;
    while (boxes[kp].pthi - boxes[kp].ptlo < n) kp = boxes[kp].mom;
    // 检查其点并保存n个最近的点。
    for (i = boxes[kp].ptlo; i <= boxes[kp].pthi; i++) {
        if (jpt == ptindex[i]) continue;
        d = disti(ptindex[i], jpt);
        if (d < dn[0]) {
            dn[0] = d;
            nn[0] = ptindex[i];
            if (n > 1) sift_down(dn, nn, n); // 维护堆结构。
        }
    }
    // 现在遍历树，仅打开可能包含更近点的盒子。
    task[1] = 0;
    ntask = 1;
    while (ntask) {
        k = task[ntask--];
        if (k == kp) continue; // 不要重复初始化时使用的盒子。
        if (dist_box[k].ptss[jpt] < dn[0]) {
            if (boxes[k].dau1) {
                task[++ntask] = boxes[k].dau1;
                task[++ntask] = boxes[k].dau2;
            } else {
                for (i = boxes[k].ptlo; i <= boxes[k].pthi; i++) {
                    d = disti(ptindex[i], jpt);
                    if (d < dn[0]) {
                        dn[0] = d;
                        nn[0] = ptindex[i];
                        if (n > 1) sift_down(dn, nn, n); // 维护堆。
                    }
                }
            }
        }
    }
    return;
}

上述例程使用以下函数对堆进行sift-down操作，它与hpsort（§8.3）中使用的sift_down仅在针对当前应用定制的接口以及同时重排两个数组（距离数组（形成堆）和对应的点编号数组）方面有所不同。

template<Int DIM> void KDtree<DIM>::sift_down(Doub *heap, Int *ndx, Int nn) {
    // 修复堆heap[0..nn-1]，其中只有第一个元素可能放错位置。
    // 在ndx[0..nn-1]中进行相应的排列。
    // 算法与hpsort中的sift_down相同。
    Int n = nn - 1;
    Int j, jold, ia;
    Doub a;
    a = heap[0];
    ia = ndx[0];
    jold = 0;
    j = 1;
    while (j <= n) {
        if (j < n && heap[j] < heap[j + 1]) j++;
        if (a >= heap[j]) break;
        heap[jold] = heap[j];
        ndx[jold] = ndx[j];
        jold = j;
        j = 2 * j + 1;
    }
    heap[jold] = a;
    ndx[jold] = ia;
}

作为最后一个说明性示例，以下是查找KD树中所有位于任意位置 $\mathbf{p}$ 的指定半径 $r$ 内的点的方法。

template<Int DIM>
Int KDtree<DIM>::locatenear(Point<DIM> pt, Doub r, Int *list, Int nmax) {
    // 给定点pt和半径r，返回值nret，使得list[0..nret-1]是
    // 所有位于pt半径r内的ktree点的列表，最多包含用户指定的nmax个点。
    Int k, i, nb, nbold, nret, ntask, jdim, d1, d2;
    Int task[50];
    nb = jdim = nret = 0;
    if (r < 0.0) throw("radius must be nonnegative");
    // 找到包含半径为r的“球”的最小盒子。
    while (boxes[nb].dau1) {
        nbold = nb;
        d1 = boxes[nb].dau1;
        d2 = boxes[nb].dau2;
        // 只需检查分割子盒子的维度。
        if (pt.x[jdim] + r <= boxes[d1].hi.x[jdim]) nb = d1;
        else if (pt.x[jdim] - r >= boxes[d2].lo.x[jdim]) nb = d2;
        jdim = ++jdim % DIM;
        if (nb == nbold) break;
    }
    // 现在仅在需要时遍历起始盒子下方的树。
    task[1] = nb;
    ntask = 1;
    while (ntask) {
        k = task[ntask--];
        if (dist_box[k].pt > r) continue;
        if (boxes[k].dau1) {
            task[++ntask] = boxes[k].dau1;
            task[++ntask] = boxes[k].dau2;
        } else {
            for (i = boxes[k].ptlo; i <= boxes[k].pthi; i++) {
                if (dist(ptss[ptindex[i]], pt) <= r && nret < nmax)
                    list[nret++] = ptindex[i];
                if (nret == nmax) return nmax;
            }
        }
    }
    return nret;
}

你可能会疑惑，为什么上述例程不利用树结构来查找完全位于半径 $r$ 的“球”内的盒子（在这种情况下，可以直接将盒子的点添加到输出列表中，而无需进一步打开其子盒子）。这种改进的潜在加速因子为 $O(\log n)$，其中 $n$ 是返回的典型邻居数量。然而，改进后的例程略长，我们无法在此包含。一个很好的练习是自己编写此修改版本。你会发现，检查一个盒子是否在球内比反过来更难：你必须检查盒子的所有 $2^D$ 个角点，而不仅仅是对角的“低”和“高”角点。

参考文献

Bentley, J.L. 1975, "Multidimensional Binary Search Trees Used for Associative Searching," Communications of the ACM, vol. 18, pp. 509–517.

de Berg, M., van Kreveld, M., Overmars, M., and Schwarzkopf, O. 2000, Computational Geometry: Algorithms and Applications, 2nd revised ed. (Berlin: Springer), §5.2.

Samet, H. 1990, The Design and Analysis of Spatial Data Structures (Reading, MA: Addison-Wesley).

21.3 二维和三维中的三角形

自欧几里得时代以来，平凡的三角形从未像今天在计算机图形学中那样受到如此多的关注。三角形和三角剖分（使用三角形分解或近似复杂几何对象）是几乎所有计算机生成图像的核心。

三个点，记作 $\mathbf{a}$、$\mathbf{b}$、$\mathbf{c}$，定义了一个三角形。它们是该三角形的顶点。如果这些点是二维的，则三角形位于二维平面内；如果这些点具有更高维度，则三角形“漂浮”在相应的 $D$ 维空间中（最常见的是 $D=3$）。目前我们仅考虑前一种情况，即 $D=2$，此时 $\mathbf{a}$ 的坐标为 $(a_0,a_1)$，$\mathbf{b}$ 和 $\mathbf{c}$ 同理。

面积。三角形 $△\mathrm{abc}$ 的面积 $\mathcal{A}(\mathrm{abc})$ 可以用多种等价方式表示，包括：

$$\begin{array}{rl}& 2\mathcal{A}(\mathbf{abc})=\left|\begin{array}{ll}{a}_0& a_1\\ b_0& b_1\\ c_0& c_1\end{array}\right|\\ & =(\mathbf{b}-\mathbf{a})\times (\mathbf{c}-\mathbf{a})=(b_0-a_0)(c_1-a_1)-(b_1-a_1)(c_0-a_0)\\ & =(\mathbf{c}-\mathbf{b})\times (\mathbf{a}-\mathbf{b})=(c_0-b_0)(a_1-b_1)-(c_1-b_1)(a_0-b_0)\\ & =(\mathbf{a}-\mathbf{c})\times (\mathbf{b}-\mathbf{c})=(a_0-c_0)(b_1-c_1)-(a_1-c_1)(b_0-c_0)\end{array}$$

此处 $\times$ 表示向量叉积，在二维情形下定义为：

$$\mathbf{A}\times \mathbf{B}=A_0{B}_1-B_1{A}_0(\mathrm{仅适用于二维})$$

稍后当我们考虑三维空间中的三角形时，公式 (21.3.1) 中的向量叉积形式将给出面积的通用公式。顺便指出，面积公式对六个坐标 $a_0$、$a_1$、$b_0$、$b_1$、$c_0$ 和 $c_1$ 分别是线性的。

公式 (21.3.1) 可能给出正值、零或负值：该面积是有符号面积。按照惯例（体现在公式 21.3.1 中），若从 $\mathbf{a}$ 到 $\mathbf{b}$ 再到 $\mathbf{c}$ 的遍历方向为逆时针（CCW），则面积为正；若为顺时针（CW），则面积为负。当且仅当三点共线时面积为零，此时三角形退化。（在后续公式中，我们通常假设非退化情形。）

绝对值 $|\mathcal{A}|$ 即为传统几何意义上的（无符号）“面积”。它也可以直接通过边长 $d_{ab}$、$d_{bc}$ 和 $d_{ca}$ 计算如下：

$$|\mathcal{A}|=\sqrt{s(s-d_{ab})(s-d_{bc})(s-d_{ca})}$$

其中 $s$ 是半周长，

$$s\equiv \frac{1}{2}(d_{ab}+d_{bc}+d_{ca})$$

（是否无需多言，边长是通过坐标差并利用毕达哥拉斯定理计算的？）

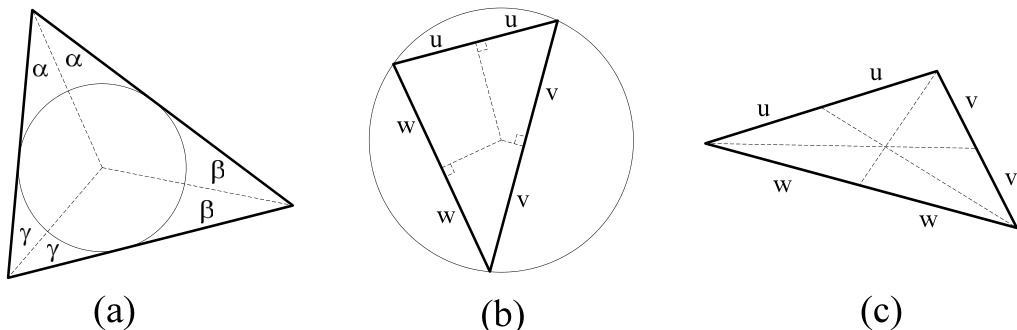
图 21.3.1. 三种三角形中心。(a) 内切圆与内心；三个顶点角的角平分线交于内心。(b) 外接圆与外心；各边的垂直平分线交于外心。(c) 重心；从各边中点到对角顶点的连线交于重心。

相关圆。每个非退化三角形都有一个内切圆（incircle），即能画在三角形内部的最大圆。内切圆与三角形的三条边均相切。从内心（内切圆的圆心）到每个顶点的连线平分该顶点处的角（见图 21.3.1）。若 $\mathbf{q}$ 为内心点，其坐标为 $(q_0,q_1)$，则其位置由下式给出：

$$q_i=\frac{1}{2s}(d_{bc}{a}_i+d_{ca}{b}_i+d_{ab}{c}_i)(i=0,1)$$

其半径为：

$$r_{\mathrm{in}}={\left(\frac{(s-d_{ab})(s-d_{bc})(s-d_{ca})}{s}\right)}^{1/2}$$

每个非退化三角形还有一个外接圆（circumcircle），即唯一通过其三个顶点的圆。设 $\mathbf{Q}$ 为外心点，其坐标为 $(Q_0,Q_1)$。令 $[ba{]}_0$ 和 $[ba{]}_1$ 分别表示坐标差 $b_0-a_0$ 和 $b_1-a_1$；$[ca{]}_0$ 和 $[ca{]}_1$ 同理。则用 $2\times 2$ 行列式形式表示为：

$$\begin{array}{rl}& Q_0=a_0+\frac{1}{2}\left|\begin{array}{ll}([ba{]}_0{)}^2+([ba{]}_1{)}^2& [ba{]}_1\\ ([ca{]}_0{)}^2+([ca{]}_1{)}^2& [ca{]}_1\end{array}\right|/\left|\begin{array}{cc}[ba{]}_0& [ba{]}_1\\ [ca{]}_0& [ca{]}_1\end{array}\right|\\ & Q_1=a_1+\frac{1}{2}\left|\begin{array}{ll}[ba{]}_0& ([ba{]}_0{)}^2+([ba{]}_1{)}^2\\ [ca{]}_0& ([ca{]}_0{)}^2+([ca{]}_1{)}^2\end{array}\right|/\left|\begin{array}{cc}[ba{]}_0& [ba{]}_1\\ [ca{]}_0& [ca{]}_1\end{array}\right|\end{array}$$

根据定义，外心到三个顶点的距离相等。因此外接圆的半径为：

$$r_{\mathrm{circum}}=\sqrt{(Q_0-a_0{)}^2+(Q_1-a_1{)}^2}$$

其中 $Q_0$ 和 $Q_1$ 由上式给出。（显然，在计算此式时，你可以先保存公式 21.3.7 中加 $a_0$ 或 $a_1$ 之前的中间结果。）

稍后在 §21.6 中，我们将大量计算外接圆。为此，我们使用以下简单的 Circle 结构体定义，以及直接实现公式 (21.3.7) 和 (21.3.8) 的 circumcircle() 函数。

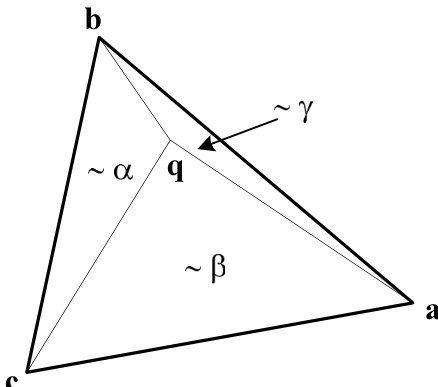
图 21.3.2. 平面内任意点 $\mathbf{q}$ 均可表示为三角形三个顶点的线性组合。系数 $(\alpha ,\beta ,\gamma )$ 称为重心坐标，其和为 1，且分别与三角形 $\Delta \mathbf{qbc}$、$\Delta \mathbf{qca}$ 和 $\Delta \mathbf{qab}$ 的面积成比例。

struct Circle {
    Point<2> center;
    Doub radius;
    Circle(const Point<2> &cen, Doub rad) : center(cen), radius(rad) {}
};

Circle circumcircle(Point<2> a, Point<2> b, Point<2> c) {
    Doub a0,a1,c0,c1,det,asq,csq,ctr0,ctr1,rad2;
    a0 = a.x[0] - b.x[0]; a1 = a.x[1] - b.x[1];
    c0 = c.x[0] - b.x[0]; c1 = c.x[1] - b.x[1];
    det = a0*c1 - c0*a1;
    if (det == 0.0) throw("no circle thru colinear points");
    det = 0.5/det;
    asq = a0*a0 + a1*a1;
    csq = c0*c0 + c1*c1;
    ctr0 = det*(asq*c1 - csq*a1);
    ctr1 = det*(csq*a0 - asq*c0);
    rad2 = ctr0*ctr0 + ctr1*ctr1;
    return Circle(Point<2>(ctr0 + b.x[0], ctr1 + b.x[1]), sqrt(rad2));
}

重心与重心坐标。三角形的重心（或称质心）$\mathbf{M}$ 与其内心和外心均不同。该点位于从每个顶点到对边中点所连线段的交点处。其坐标即为各顶点坐标的平均值：

$$M_i=\frac{1}{3}(a_i+b_i+c_i)(i=0,1)$$

重心 $\mathbf{M}$ 也是使得面积 $\mathcal{A}(\mathbf{abM})$、$\mathcal{A}(\mathbf{bcM})$ 和 $\mathcal{A}(\mathbf{caM})$ 均相等的点。在 §21.7 中，我们将使用三角网格对函数进行插值。重心的意义在于，线性插值函数在该点的取值等于三个顶点处函数值的平均值。

事实上，推广重心的概念，平面内任意点 $\mathbf{q}$ 均可表示为三个顶点 $\mathbf{a}$、$\mathbf{b}$、$\mathbf{c}$ 的线性组合，且组合系数之和为 1。这些系数称为 $\mathbf{q}$ 的重心坐标，可直观地用三角形面积公式表示（见图 21.3.2）。相关方程为

$$\begin{array}{r}\mathbf{q}=\alpha \mathbf{a}+\beta \mathbf{b}+\gamma \mathbf{c}\\ \alpha =\mathcal{A}(\mathbf{bcq})/\mathcal{A}(\mathbf{abc})\\ \beta =\mathcal{A}(\mathbf{caq})/\mathcal{A}(\mathbf{abc})\\ \gamma =\mathcal{A}(\mathbf{abq})/\mathcal{A}(\mathbf{abc})\end{array}$$

根据构造，有

$$\alpha +\beta +\gamma =1$$

因此，方程 (21.3.10) 的第一行等价于

$$\mathbf{q}=\mathbf{c}+\alpha (\mathbf{a}-\mathbf{c})+\beta (\mathbf{b}-\mathbf{c})$$

这可以看作是一个坐标变换的方程，它将 $(\alpha ,\beta )$ 坐标变换为 $(q_0,q_1)$ 坐标。显然，由于该变换是线性的，其逆变换——即方程 (21.3.10) 中 $\alpha$ 和 $\beta$ 的表达式——也必然是线性的。这一点我们早已知晓，因为我们之前已经注意到面积公式 (21.3.1) 对所有坐标都是线性的，特别是对 $q_0$ 和 $q_1$ 也是线性的。重心坐标可以以一种有用的方式推广到三维或更高维空间中的三角形，我们将在下文看到这一点。

注意，当点 $\mathbf{q}$ 分别趋近于 $\mathbf{a}$、$\mathbf{b}$ 或 $\mathbf{c}$ 时，$\alpha$、$\beta$ 或 $\gamma$ 会趋近于 1；并且在三角形的任意一条边上（例如 $\overline{ab}$），对顶点（此处为 $\gamma$）的系数会变为零。点 $\mathbf{q}$ 位于三角形 $\Delta \mathbf{abc}$ 内部，当且仅当 $\alpha$、$\beta$ 和 $\gamma$ 均为正数。事实上，这是判断一个点是否在三角形内部的一个好方法。（在此应用中，你当然可以省略分母面积的计算。）

当你希望在 $\Delta \mathbf{abc}$ 内部均匀随机地选取一个点 $\mathbf{q}$ 时，重心坐标也非常有用：首先在 $(0,1)$ 区间内分别均匀随机地选取 $\alpha$ 和 $\beta$。接着，如果 $\alpha +\beta >1$，则对两者进行如下修正：$\alpha \leftarrow 1-\alpha$ 和 $\beta \leftarrow 1-\beta$。最后，应用方程 (21.3.12)。其思想是，最初选取的 $\alpha$ 和 $\beta$ 在由三角形两边张成的平行四边形内是均匀随机的；如果该点落在对角线的错误一侧，我们就通过对称反射将其移动到正确的一侧。

21.3.1 三维空间中的三角形

我们所关注的三角形仍然由三个点 $\mathbf{a}$、$\mathbf{b}$ 和 $\mathbf{c}$ 定义，但现在这些点位于三维空间中，其坐标（以 $\mathbf{a}$ 为例）为 $(a_0,a_1,a_2)$。有向面积 $\mathcal{A}$（方程 21.3.1）的推广现在是一个矢量面积 $\overrightarrow{\mathcal{A}}$，其方向垂直于三角形所在平面，长度等于三角形的面积。它最方便地用三维空间中的矢量叉积表示：

$$\begin{array}{rl}& \mathbf{A}\times \mathbf{B}=\left|\begin{array}{lll}{\hat{\mathbf{e}}}_0& {\hat{\mathbf{e}}}_1& {\hat{\mathbf{e}}}_2\\ A_0& A_1& A_2\\ B_0& B_1& B_2\end{array}\right|\\ & =(A_1{B}_2-A_2{B}_1){\hat{\mathbf{e}}}_0+(A_2{B}_0-A_0{B}_2){\hat{\mathbf{e}}}_1+(A_0{B}_1-A_1{B}_0){\hat{\mathbf{e}}}_2\end{array}$$

其中 ${\hat{\mathbf{e}}}_0$、${\hat{\mathbf{e}}}_1$ 和 ${\hat{\mathbf{e}}}_2$ 分别是单位矢量 $(1,0,0)$、$(0,1,0)$ 和 $(0,0,1)$。于是我们有（参见方程 21.3.1）：

$$\begin{array}{rl}& 2\overrightarrow{A}(\mathbf{abc})=(\mathbf{b}-\mathbf{a})\times (\mathbf{c}-\mathbf{a})\\ & =(\mathbf{c}-\mathbf{b})\times (\mathbf{a}-\mathbf{b})\\ & =(\mathbf{a}-\mathbf{c})\times (\mathbf{b}-\mathbf{c})\end{array}$$

你可以通过对 $\overrightarrow{\mathcal{A}}$ 的三个分量平方和开平方根来计算正标量面积 $\mathcal{A}\equiv |\overrightarrow{\mathcal{A}}|$；或者也可以使用方程 (21.3.3)，其中 $d_{ab}=|\mathbf{a}-\mathbf{b}|$ 等。

由三角形定义的平面。一个点 $\mathbf{q}$ 位于由 $△\mathbf{abc}$ 定义的平面上，当且仅当四面体 $\mathbf{abcq}$ 的体积为零。一般而言，四面体的体积由下式给出：

$$\begin{array}{rl}& 6\mathcal{V}=\left|\begin{array}{llll}{a}_0& a_1& a_2& 1\\ b_0& b_1& b_2& 1\\ c_0& c_1& c_2& 1\\ q_0& q_1& q_2& 1\end{array}\right|\\ & =(\mathbf{b}-\mathbf{a})\cdot [(\mathbf{c}-\mathbf{a})\times (\mathbf{q}-\mathbf{a})]\\ & =(\mathbf{c}-\mathbf{a})\cdot [(\mathbf{q}-\mathbf{a})\times (\mathbf{b}-\mathbf{a})]\\ & =(\mathbf{q}-\mathbf{a})\cdot [(\mathbf{b}-\mathbf{a})\times (\mathbf{c}-\mathbf{a})]\end{array}$$

其中“$\cdot$”表示矢量点积。你还可以在上式中对 $\mathbf{a}$、$\mathbf{b}$ 和 $\mathbf{c}$ 进行循环置换，从而得到看似无穷多种形式但实质相同的公式！

体积 $\mathcal{V}$ 是有符号的，当从外部（远离 $\mathbf{q}$ 的一侧）观察时，若 $\Delta \mathbf{abc}$ 为逆时针方向，则 $\mathcal{V}$ 为正，即右手定则给出一个向外的法向量。

方程 (21.3.15) 的最后一种形式特别简洁，因为将其设为零即可得到由 $\Delta \mathbf{abc}$ 定义的平面上任意点 $\mathbf{q}$ 所满足的方程：

$$\mathbf{q}\cdot \mathbf{N}=D$$

其中

$$\begin{array}{rl}& \mathbf{N}=(\mathbf{b}-\mathbf{a})\times (\mathbf{c}-\mathbf{a})(\mathrm{或}\mathbf{a},\mathbf{b},\mathbf{c}\text{ 的循环置换})\\ & D=\mathbf{a}\cdot \mathbf{N}(或者，同样地，=\mathbf{b}\cdot \mathbf{N}=\mathbf{c}\cdot \mathbf{N}\end{array}$$

我们也可以将方程 (21.3.16) 两边除以 $|\mathbf{N}|$，此时左边的矢量变为 $\hat{\mathbf{N}}=\mathbf{N}/|\mathbf{N}|$，即平面的单位法向量，而 $\hat{D}=D/|\mathbf{N}|$ 则表示平面到原点的距离。

利用相同的工具，我们可以轻松地将任意点 $\mathbf{p}$ 投影到一个新的点 ${\mathbf{p}}^{\prime }$，使其位于 $\Delta \mathbf{abc}$ 的平面上：

$$\mathbf{p}⟶{\mathbf{p}}^{\prime }=\mathbf{p}+\frac{[(\mathbf{a}-\mathbf{p})\cdot \mathbf{N}]\mathbf{N}}{|\mathbf{N}{|}^2}$$

其中 $\mathbf{N}$ 如上所述。在此公式中，$\mathbf{a}$ 可以替换为 $\mathbf{b}$、$\mathbf{c}$ 或平面上任意其他点。

我们可以通过依次投影一个三角形的三个顶点，将其投影到另一个三角形所定义的平面上。（这是在将三维三角网格模型渲染到计算机屏幕的二维“相机平面”时非常常见的操作。）

重心坐标。对于位于三角形平面内的点 $\mathbf{q}$，重心坐标在三维空间中依然有效，特别是方程 (21.3.10) 仍然成立。原则上，可以通过 (21.3.14) 计算各个 $\mathcal{A}$ 来求得 $(\alpha ,\beta )$，但一种更简便的等效计算方法是：

$$\begin{array}{r}\alpha =\frac{{\mathbf{b}}^{\prime 2}({\mathbf{a}}^{\prime }\cdot {\mathbf{q}}^{\prime })-({\mathbf{a}}^{\prime }\cdot {\mathbf{b}}^{\prime })\left({\mathbf{b}}^{\prime }\cdot {\mathbf{q}}^{\prime }\right)}{{\mathbf{a}}^{\prime 2}{\mathbf{b}}^{\prime 2}-({\mathbf{a}}^{\prime }\cdot {\mathbf{b}}^{\prime }{)}^2}\\ \beta =\frac{{\mathbf{a}}^{\prime 2}({\mathbf{b}}^{\prime }\cdot {\mathbf{q}}^{\prime })-({\mathbf{a}}^{\prime }\cdot {\mathbf{b}}^{\prime })\left({\mathbf{a}}^{\prime }\cdot {\mathbf{q}}^{\prime }\right)}{{\mathbf{a}}^{\prime 2}{\mathbf{b}}^{\prime 2}-({\mathbf{a}}^{\prime }\cdot {\mathbf{b}}^{\prime }{)}^2}\end{array}$$

（只需计算一次相同的分母），其中

$${\mathbf{a}}^{\prime }\equiv \mathbf{a}-\mathbf{c},{\mathbf{b}}^{\prime }\equiv \mathbf{b}-\mathbf{c},{\mathbf{q}}^{\prime }\equiv \mathbf{q}-\mathbf{c}$$

顺便提一下，如果 $\mathbf{q}$ 不在 $\Delta \mathbf{abc}$ 所在的平面内，你仍然可以使用公式 (21.3.19)。在这种情况下，你会得到该点在平面上投影后的 $(\alpha ,\beta )$ 坐标。此外，请注意一种特殊情况：当 $\Delta \mathbf{abc}$ 是一个直角三角形，直角顶点为 $\mathbf{c}$，且边 $\overline{ac}$ 和 $\overline{bc}$ 的长度均为单位长度（即 $d_{ac}=d_{bc}=1$）时，两个方向上的坐标变换就变得非常简单：

$$\begin{array}{r}\mathbf{q}=\mathbf{c}+\alpha (\mathbf{a}-\mathbf{c})+\beta (\mathbf{b}-\mathbf{c})\\ [\alpha ,\beta ]=[(\mathbf{a}-\mathbf{c})\cdot (\mathbf{q}-\mathbf{c}),(\mathbf{b}-\mathbf{c})\cdot (\mathbf{q}-\mathbf{c})]\end{array}$$

换句话说，我们只需通过将原点平移到 $\mathbf{c}$，然后分别与两个“坐标轴” $\mathbf{a}-\mathbf{c}$ 和 $\mathbf{b}-\mathbf{c}$ 做点积，即可将点投影到平面内的标准正交坐标系中。

在三维空间中，当一个平面由一个三角形（或可由一个三角形表示）定义时，重心坐标通常是进行平面内操作的首选坐标系统。一个简单的例子是：我们可以利用公式 (21.3.19)（或适用时的公式 21.3.21）计算出 $\alpha$ 和 $\beta$，然后检查 $\alpha$、$\beta$ 以及 $\gamma =1-\alpha -\beta$ 是否均为正数，从而判断投影点 ${\mathbf{p}}^{\prime }$ 是否位于 $\Delta \mathbf{abc}$ 内部。

两个三角形之间的夹角：两个三角形（例如共享一条边的两个三角形）之间的二面角等于它们法向量之间的夹角。法向量可由向量面积公式 (21.3.14) 给出。该夹角最好使用下一节中的公式 (21.4.13) 来计算。

参考文献

Bowyer, A. and Woodwark, J. 1983, A Programmer's Geometry (London: Butterworths), Chapter 4.

Schneider, P.J. and Eberly, D.H. 2003, Geometric Tools for Computer Graphics (San Francisco: Morgan Kaufmann), §3.5 and Appendix C.

López-López, F.J. 1992, "Triplets Revisited," in Graphics Gems III, Kirk, D., ed. (Cambridge, MA: Academic Press).

Glassner, A.S. 1990, "Useful 3D Geometry," in Graphics Gems, Glassner, A.S., ed. (San Diego: Academic Press).

21.4 直线、线段与多边形

一条直线可由其经过的任意两点定义，记为 $\mathbf{a}$ 和 $\mathbf{b}$。如 §21.1 中所述，若所关注的区域是一个平面，则这些点可以是二维的；若直线嵌入在更高维空间中，则这些点可以是三维（或更高维）的。目前，我们仅考虑二维情形。

参数化地表示，位于由 $\mathbf{a}$ 和 $\mathbf{b}$ 定义的直线上的任意点 $\mathbf{c}$ 必定是这两个点的线性组合。一种写法是：

$$\mathbf{c}=\mathbf{a}+s(\mathbf{b}-\mathbf{a})(-\infty <s<\infty )$$

其中 $s$ 是沿直线的参数。此处的归一化方式使得在 $\mathbf{a}$ 处 $s=0$，在 $\mathbf{b}$ 处 $s=1$。当 $0\le s\le 1$ 时，对应的是 $\mathbf{a}$ 与 $\mathbf{b}$ 之间的线段，记作 $\overline{\mathbf{ab}}$。整条直线则记作 $\overleftrightarrow{\mathbf{ab}}$。

要得到直线 $\overleftrightarrow{\mathbf{ab}}$ 上所有点 $\mathbf{c}$ 满足的方程，最简单的方法是对公式 (21.4.1) 两边右乘向量叉积 $(\mathbf{b}-\mathbf{a})$。利用任意向量与其自身的叉积为零这一性质，可得：

$$\mathbf{c}\times (\mathbf{b}-\mathbf{a})=\mathbf{a}\times \mathbf{b}$$

或者展开成分量形式：

$$c_0(b_1-a_1)-c_1(b_0-a_0)=a_0{b}_1-a_1{b}_0$$

这确实是坐标 $c_0$ 与 $c_1$ 之间的线性关系。虽然我们可能会想将该方程除以 $b_0-a_0$，从而得到熟悉的中学形式“$y=mx+b$”，但通常应避免这样做，因为如公式 (21.4.3) 所示，它在垂直直线（即 $b_0-a_0=0$）的情况下依然有效。

两条直线的交点：在平面中，两条直线 $\overleftrightarrow{\mathbf{ab}}$ 与 $\overleftrightarrow{\mathbf{xy}}$ 通常都会相交。我们可以通过令两条直线的参数形式相等来求解交点：

$$\mathbf{a}+s(\mathbf{b}-\mathbf{a})=\mathbf{x}+t(\mathbf{y}-\mathbf{x})$$

然后解这两个方程（分别对应第 0 和第 1 个分量）以求出两个未知数 $s$ 和 $t$。结果为：

$$\begin{array}{r}s=\frac{(\mathbf{x}-\mathbf{y})\times (\mathbf{a}-\mathbf{x})}{(\mathbf{b}-\mathbf{a})\times (\mathbf{x}-\mathbf{y})}=\frac{(x_0-y_0)(a_1-x_1)-(x_1-y_1)(a_0-x_0)}{(b_0-a_0)(x_1-y_1)-(b_1-a_1)(x_0-y_0)}\\ t=\frac{(\mathbf{a}-\mathbf{x})\times (\mathbf{b}-\mathbf{a})}{(\mathbf{b}-\mathbf{a})\times (\mathbf{x}-\mathbf{y})}=\frac{(a_0-x_0)(b_1-a_1)-(a_1-x_1)(b_0-a_0)}{(b_0-a_0)(x_1-y_1)-(b_1-a_1)(x_0-y_0)}\end{array}$$

当然，当分母为零时，表示两条直线平行且无交点。

这么多叉积可能会让你觉得公式 (21.4.5) 具有某种几何意义。确实如此。如图 21.4.1 所示，两条直线在点 $\mathbf{o}$ 相交。因此，线段 $\overline{\mathbf{xo}}$ 是 $\overline{\mathbf{xy}}$ 按比例 $t$ 缩放后的结果，而 $\overline{\mathbf{ao}}$ 则是 $\overline{\mathbf{ab}}$ 按比例 $s$ 缩放后的结果。因此，三角形 $△\mathbf{oxa}$ 的面积（参见公式 21.3.1）为：

$$2\mathcal{A}(\mathbf{oxa})=st(\mathbf{x}-\mathbf{y})\times (\mathbf{a}-\mathbf{b})$$

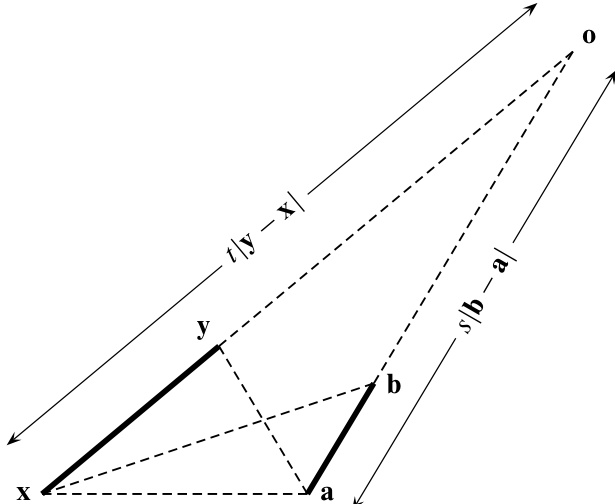
图 21.4.1：通过三角形面积之比构造两条直线交点的几何示意图。详见正文。

由于三角形面积与其高呈线性关系（底边固定），我们还有

$$\begin{array}{rl}\mathcal{A}(\mathbf{oxa})/\mathcal{A}(\mathbf{yxa})=t& \mathcal{A}(\mathbf{oxa})/\mathcal{A}(\mathbf{bxa})=s\end{array}$$

式 (21.4.5) 可直接由这些关系和式 (21.3.1) 推出。

点到直线的距离。任意点 $\mathbf{q}$ 到穿过点 $\mathbf{a}$ 和 $\mathbf{b}$ 的直线 $\overleftrightarrow{\mathbf{ab}}$ 的垂直距离 $d$ 是多少？显然，当以线段 $\mathbf{ab}$ 为底边时，$d$ 就是三角形 $\Delta \mathbf{abq}$ 的高。因此，根据中学课本中“底乘高除以二”的面积公式，有：

$$d=\frac{2\mathcal{A}(\mathbf{abq})}{|\mathbf{a}-\mathbf{b}|}=\frac{(q_0-b_0)(a_1-b_1)-(q_1-b_1)(a_0-b_0)}{\sqrt{(a_0-b_0{)}^2+(a_1-b_1{)}^2}}$$

注意，$d$ 是带符号的：若点 $\mathbf{q}$ 位于从 $\mathbf{a}$ 指向 $\mathbf{b}$ 的有向直线左侧，则 $d$ 为正；若位于右侧，则为负。这也自然引出了我们下一个话题。

21.4.1 线段相交与“左侧”关系

你可以利用式 (21.4.5) 来判断两条线段 $\overline{\mathbf{ab}}$ 与 $\overline{\mathbf{xy}}$ 是否相交：计算 $s$ 和 $t$，然后检查它们是否都在区间 $(0,1)$ 内。（为简洁起见，我们在此及后续内容中不会详细讨论 $s$ 或 $t$（或两者）恰好等于 0 或 1 的各种退化情形。如果你的应用需要处理这些情况，它们其实很容易处理。）

另一种相关但略有不同的方法是利用式 (21.3.1) 中三角形面积公式的符号性质。这意味着以下两个陈述是等价的：

$$\mathcal{A}(\mathbf{abc})>0⟺\lceil \mathbf{c}\text{ 在从 }\mathbf{a}\text{ 到 }\mathbf{b}\text{ 方向遍历的直线 }\overleftrightarrow{\mathbf{ab}}\text{ 的左侧}\rceil$$

而 $\mathcal{A}(\mathbf{abc})<0$ 则意味着 $\mathbf{c}$ 位于同一直线的右侧。我们将式 (21.4.9) 中的任一陈述称为“左侧关系”（left-of relation）。

两条线段 $\overline{\mathbf{ab}}$ 与 $\overline{\mathbf{xy}}$ 相交的充要条件是：$\mathbf{x}$ 与 $\mathbf{y}$ 位于 $\overleftarrow{\mathbf{ab}}$ 的两侧，且 $\mathbf{a}$ 与 $\mathbf{b}$ 位于 $\overleftarrow{\mathbf{x}\overrightarrow{\mathbf{y}}}$ 的两侧。（我们再次省略对各种共线特殊情况的讨论。）该测试利用式 (21.3.1) 中的三角形面积公式，需计算四个“左侧关系”，每个在计算上对应一个叉积，这比计算 $s$ 和 $t$（它们共享一个分母）略多一点工作量。然而，你有时可以在计算的其他部分重复使用已计算出的叉积。因此，使用“$s,t$”方法还是“左侧”方法往往难分优劣——你应考虑两种方法。

表 21.4.1 列出了对两条线段计算所有四种可能的“左侧”测试时得到的 16 种情况。（实际上，只有 14 种在几何上是可能的！）该表对每种可能性进行了分类：线段是否相交（用 $\times$ 表示相交，注意不要与向量叉积混淆！）、一条线段的单向延长线（射线）是否与另一条线段相交，或者（最后一种情况）两条直线的交点是否位于两条线段之外。表中还给出了每种情况下两条线段的外凸包（包含两条线段的最小三角形或四边形）及其顺时针遍历顺序。图 21.4.2 展示了每种可能性的一个示例。

你可以利用该表找出用于测试特定情形的组合。

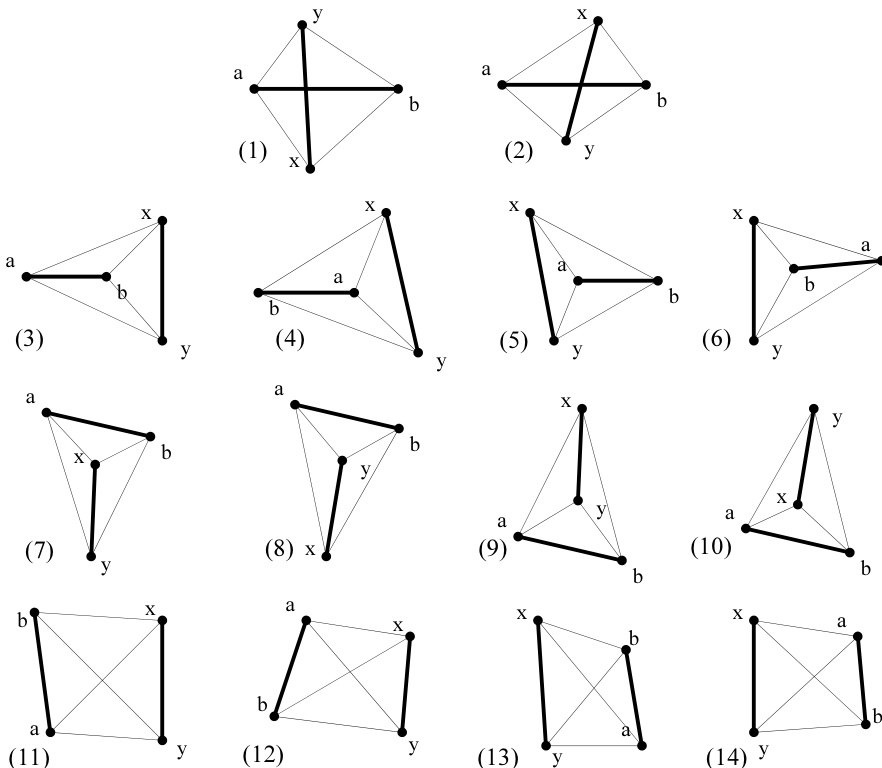
图 21.4.2. 两条线段 $ab$ 与 $xy$ 定义了四个三角形（$\Delta abx$、$\Delta aby$、$\Delta xya$ 和 $\Delta xyb$），每个三角形的面积可正可负。在 16 种符号组合中，有 14 种（如图所示）对应于线段或其射线延长线之间可能的相交关系。

例如，如果你需要测试射线 $\overline{\mathbf{ab}}$ 是否与线段 $\overline{\mathbf{xy}}$ 相交（包括线段本身相交的情况），你可以查看表中的第 1、2、3 和 6 行，并读出一个仅涉及三个“左侧关系”的测试条件：

$$\begin{array}{r}\mathcal{A}(\mathbf{abx})\mathcal{A}(\mathbf{aby})<0\mathrm{且}\mathcal{A}(\mathbf{aby})\mathcal{A}(\mathbf{xya})>0\end{array}$$

当然，对于此例，使用 $s$ 和 $t$ 也存在完全等价的测试条件（其中 $s$ 和 $t$ 如式 21.4.4 所定义）：$s>0$ 且 $0<t<1$。

两向量间的夹角。设 $\mathbf{U}$ 和 $\mathbf{V}$ 分别为两条直线上的差向量，$\theta$ 为两直线间的夹角（从 $\mathbf{U}$ 测量到 $\mathbf{V}$）。用前述符号表示，即 $\mathbf{U}=\mathbf{y}-\mathbf{x}$，$\mathbf{V}=\mathbf{b}-\mathbf{a}$。初等向量分析告诉我们：

$$\begin{array}{r}\mathbf{U}\cdot \mathbf{V}=U_0{V}_0+U_1{V}_1=|\mathbf{U}||\mathbf{V}|\cos (\theta )\\ \mathbf{U}\times \mathbf{V}=U_0{V}_1-U_1{V}_0=|\mathbf{U}||\mathbf{V}|\sin (\theta )\end{array}$$

许多人试图通过上述关系之一，计算向量的模长并取反余弦或反正弦来求 $\theta$。这是个大错误！不仅反三角函数存在象限歧义，而且在正弦和余弦函数接近极值（平坦区域）的角度附近，你可能会损失多达一半的有效数字。更不用说还需要计算模长的平方根了！更好的方法是：

$$\theta =atan2(\mathbf{U}\times \mathbf{V},\mathbf{U}\cdot \mathbf{V})=atan2(U_0{V}_1-U_1{V}_0,U_0{V}_0+U_1{V}_1)$$

其中 atan2() 是 C 或 C++ 中的象限敏感反正切函数。该函数允许任一参数为零，并返回 $-\pi$ 到 $\pi$ 范围内的值。（Fortran 和大多数其他语言中也存在相同的函数。）

21.4.2 三维空间中的直线

将式 (21.4.12) 直接推广到三维空间，可得两个三维向量之间的夹角：

$$\theta =atan2(|\mathbf{U}\times \mathbf{V}|,\mathbf{U}\cdot \mathbf{V})$$

注意此处出现了向量叉积的模长，这需要计算平方根。

由于篇幅限制，我们只能对三维空间中的直线再多说一点。参数化形式

$$\mathbf{c}=\mathbf{a}+s\mathbf{v}(-\infty <s<\infty )$$

（即式 21.4.1，其中 $\mathbf{v}\equiv \mathbf{b}-\mathbf{a}$）仍然适用，只是现在 $\mathbf{a}$、$\mathbf{v}$ 和 $\mathbf{c}$ 是三维空间中的点。直线与由 $\mathbf{N}$ 和 $D$ 定义的平面（见式 21.3.16）相交时的参数 $s$ 为：

$$s=\frac{D-\mathbf{a}\cdot \mathbf{N}}{\mathbf{v}\cdot \mathbf{N}}$$

当直线与平面平行时，分母为零。

一条直线到点 $\mathbf{q}$ 的最近距离出现在以下参数值处：

$$s=\frac{(\mathbf{q}-\mathbf{a})\cdot \mathbf{v}}{|\mathbf{v}{|}^2}$$

你也可以利用这一点来判断一条直线是否与三维空间中的球体相交：计算直线上离球心最近的点，然后检查该点到球心的距离是否小于球的半径（或者比较距离的平方以避免开方运算）。

一般而言，两条直线（记为 $\mathbf{a}+s\mathbf{v}$ 和 $\mathbf{x}+t\mathbf{u}$）不会相交，而是彼此呈异面（skew）关系。然而，它们之间的最近点参数可按如下公式计算 [2]：

$$s=\frac{\det \left\{(\mathbf{a}-\mathbf{x}),\mathbf{u},\mathbf{u}\times \mathbf{v}\right\}}{|\mathbf{u}\times \mathbf{v}{|}^2}t=\frac{\det \left\{(\mathbf{a}-\mathbf{x}),\mathbf{v},\mathbf{u}\times \mathbf{v}\right\}}{|\mathbf{u}\times \mathbf{v}{|}^2}$$

其中 $\det$ 表示一个 $3\times 3$ 的行列式，其各列为所指定的三个三维向量。当两条直线平行时，分母为零。如果你确实需要检查是否存在实际交点，可将上述 $s$ 和 $t$ 代入各自直线的参数方程，然后检查所得两点之间的距离是否小于某个舍入误差容限。

计算机图形学中一个常见的操作是判断一条直线是否与三维空间中的三角形相交。使用前面讨论过的方法，可以先用公式 (21.3.17) 求出三角形所在平面的法向量 $\mathbf{N}$ 和常数项 $D$；然后利用公式 (21.4.14) 和 (21.4.15) 求出直线与该平面的交点；最后用公式 (21.3.19) 求出该交点的重心坐标 $\alpha$ 和 $\beta$。若 $\alpha$、$\beta$ 以及 $\gamma \equiv 1-\alpha -\beta$ 均为正数，则交点位于三角形内部。关于如何优化该过程，参见 [4,1]。

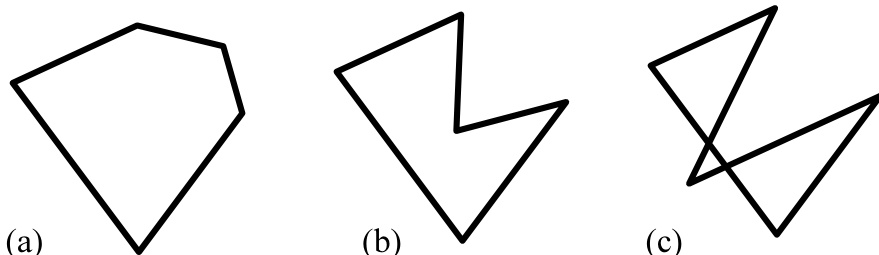
图 21.4.3. 若多边形没有相交的边（如 (a) 和 (b) 所示），则称为简单多边形；否则称为复杂多边形（如 (c) 所示）。简单多边形又可分为凸多边形（a）和凹多边形（b）。

21.4.3 多边形

我们将多边形定义为由 $N$ 个点（顶点）组成的向量，编号从 0 到 $N-1$，以及按循环顺序连接这些点的 $N$ 条有向线段，即从 0 到 1、1 到 2、……、$N-2$ 到 $N-1$，以及（重要的是！）从 $N-1$ 回到 0。（在下面某些公式中，我们采用约定：顶点 $N$ 即指顶点 0。）

如果两个多边形仅在顶点编号上相差一个循环移位，但所有线段都相同，则我们认为它们是同一个多边形。然而，如果我们反转遍历顶点的顺序，则认为所得多边形是不同的（例如，其面积符号会改变）。如果一个区域的边界无法用单个循环向量遍历（例如，一个外正方形与一个内嵌三角形之间的区域），我们就不称其为多边形；当然，也可以采用其他约定。

根据上述定义，我们可以将多边形分为两类：简单多边形（即其 $N$ 条边互不相交）和复杂多边形（存在一条或多条边相交）。对于简单多边形，我们进一步根据其是否为凸多边形或凹多边形进行分类。凸多边形可定义为满足以下任一条件的多边形：(i) 任意两个顶点之间的所有 $N(N-1)/2$ 条连线都位于其内部（或边界上）；(ii) 所有外角符号相同（允许为零）。无论采用哪一性质作为定义，另一性质就成为定理。图 21.4.3 展示了这三种类型的例子。

对于简单多边形，其外角之和恒为 $\pm 2\pi$。也就是说，当你绕多边形一周时，总共转过的角度恰好是一个完整的圆周。如果多边形是凹的，则在求和时必须考虑外角的符号。这一点在图 21.4.4 中有所展示。当按逆时针（CCW）方向遍历时，$2\pi$ 的符号为正；顺时针（CW）方向则为负。

复杂（即自相交）多边形的外角之和也可能等于 $2\pi$，如图 21.4.3(c) 所示，因此外角之和通常并不能提供一种神奇的方法来检测边的相交情况。然而，存在一个小小的“魔法”：如果一个多边形的所有外角符号相同（或为零），且其总和为 $\pm 2\pi$，则该多边形既是简单多边形又是凸多边形。这提供了一种非常快速的判断简单凸多边形的方法，但它无法区分简单凹多边形和复杂多边形。要实现这种区分，必须详细检查是否存在相交的边（我们将在下面的代码中实现这一检查）。

环绕数（Winding Number）。假设你坐在平面上某一点 $p$，观察某人绕一个多边形行驶，那么他绕你行驶的净圈数（按通常的符号约定，逆时针为正）即为该多边形相对于该点的环绕数。对于简单多边形，环绕数在以下情况下成立：

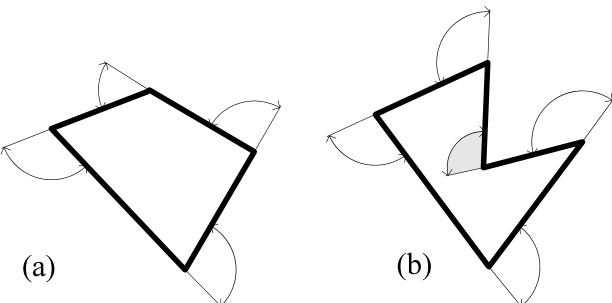
图 21.4.4. 简单多边形的外角之和等于一个完整圆周。(a) 若多边形为凸，则所有外角符号相同。(b) 若多边形为凹，则一个或多个外角（此处为阴影角）符号相反。

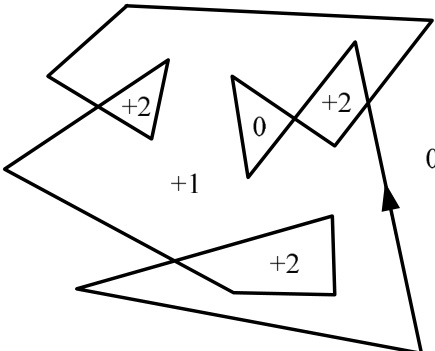
图 21.4.5. 复杂多边形在不同区域内的环绕数（以整数标出）不同。该多边形的总环绕数（外角之和除以 $2\pi$）为 3，但没有任何单一区域实现该值。注意，复杂多边形的内部区域也可能具有环绕数 0。

对于逆时针（CCW）多边形内部的点，环绕数为 1；对于顺时针（CW）多边形内部的点，环绕数为 $-1$；对于外部点，环绕数为 0。但对于复杂多边形，情况则没有这么简单。图 21.4.5 展示了一个复杂情形。注意，复杂多边形的某些内部区域可能具有环绕数 0，因此仅凭某点的环绕数无法判断其是否位于复杂多边形内部。此外，多边形外角之和除以 $2\pi$ 所得的值，不一定等于该多边形相对于平面上任意点的环绕数。

计算多边形相对于点 $\mathbf{q}$ 的环绕数，最糟糕的方法莫过于将 $\mathbf{q}$ 与多边形连续顶点 ${\mathbf{p}}_i$ 之间的 $N$ 个增量角度相加，即：

$$W.N.(\mathbf{q})=\frac{1}{2\pi }\sum _{i=0}^{N-1}\angle ({\mathbf{p}}_{i+1}\mathbf{q}{\mathbf{p}}_i)$$

（采用通常约定 ${\mathbf{p}}_N\equiv {\mathbf{p}}_0$）。即使使用公式 (21.4.12) 中的技巧来计算角度，这种方法仍包含大量不必要的计算。

更高效的方法是注意到：如果一个多边形绕 $\mathbf{q}$ 转了 $M$ 圈，那么其边必定与从 $\mathbf{q}$ 向无穷远延伸的任意射线净相交 $M$ 次，其中逆时针方向的穿越计为正，顺时针方向计为负。特别地，如果我们取该射线为从 $\mathbf{q}$ 向右的水平射线，就可以立即排除那些不与包含 $\mathbf{q}$ 的水平线相交的边，然后通过一次“左侧测试”（"left-of" test）[5] 来判断射线穿越及其符号。这些思想体现在以下例程中。

Int polywind(const vector< Point<2> > &vt, const Point<2> &pt) {
    // 返回多边形（由顶点向量 vt 指定）相对于任意点 pt 的环绕数。
    Int i, np, wind = 0;
    Doub d0,d1,p0,p1,pt0,pt1;
    np = vt.size();
    pt0 = pt.x[0];
    pt1 = pt.x[1];
    p0 = vt[np-1].x[0];
    p1 = vt[np-1].x[1];
    for (i=0; i<np; i++) {
        d0 = vt[i].x[0];
        d1 = vt[i].x[1];
        if (p1 <= pt1) {
            if (d1 > pt1 && (p0-pt0)*(d1-pt1)-(p1-pt1)*(d0-pt0) > 0) wind++;
        }
        else {
            if (d1 <= pt1 && (p0-pt0)*(d1-pt1)-(p1-pt1)*(d0-pt0) < 0) wind--;
        }
        p0 = d0;
        p1 = d1;
    }
    return wind;
}

是否存在一种同样高效的方法来计算多边形 ${\mathbf{p}}_i$（$i=0,\dots ,N-1$）的总环绕数（即其外角之和除以 $2\pi$）？答案是肯定的。考虑一个导出多边形，其顶点 ${\mathbf{q}}_i$ 由向量差给出：

$${\mathbf{q}}_i={\mathbf{p}}_{i+1}-{\mathbf{p}}_i(i=0,\dots ,N-1)$$

那么该导出多边形相对于原点的环绕数，就等于原多边形的总环绕数。（如果不明显，请画图理解。）可使用例程 polywind() 进行该计算。

点是否在多边形内。如何判断一个任意点 $\mathbf{q}$ 是否位于多边形内部或外部 [5]？首先假设你的多边形是简单多边形。对于简单多边形，常用的两种方法是“环绕数法”和“若尔当曲线定理法”。然而，当这两种方法都被高效实现时，它们几乎完全相同！

环绕数法就是计算多边形相对于该点的环绕数（例如，使用上面的 polywind() 函数）。如果结果为 ±1，则该点在多边形内部；如果为零，则在外部。任何其他结果都表明该多边形并非如假设那样是简单多边形。

Jordan曲线定理方法指出：从该点向无穷远处引出的任意射线，若该点在多边形内部，则射线与多边形边界相交奇数次；若该点在外部，则相交偶数次［见图21.4.6(a)］。如果我们在代码中实现这一方法，其代码将与polywind函数几乎完全相同，只有一个细节不同：在每次射线与边相交时，我们不再根据交叉方向对计数器进行增减，而是始终递增计数器。最后，我们只需

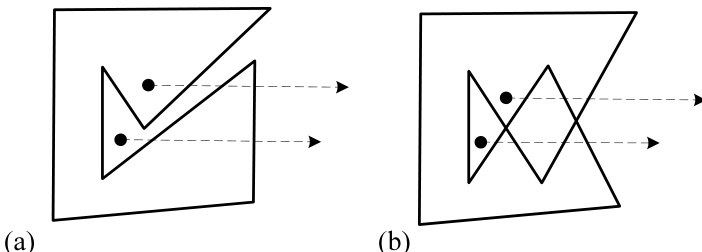
图21.4.6. 如何判断一个点是否在多边形内部？(a) 对于简单多边形，既可以使用环绕数方法，也可以使用Jordan曲线定理（判断射线与边界的交点数为奇数还是偶数）。(b) 对于复杂多边形，则不存在简单的判断方法。

检查计数器是奇数还是偶数即可。但若按原样实现的polywind函数返回0，则说明它遇到的递增次数与递减次数相等，即总交叉次数为偶数；而若它返回±1（对于简单多边形，这是唯一可能的其他返回值），则说明总交叉次数为奇数。因此，这两种方法实际上是等价的。

如果你的多边形不是简单多边形怎么办？如图21.4.6(b)所示，此时情况变得复杂。环绕数方法和Jordan曲线定理方法都会判定图中上方的点位于所示复杂多边形的内部，这在直观上似乎是正确的。然而，这两种方法都会判定下方的点位于多边形外部。事实上，确实存在一些自洽的“内部性”定义方式，使得这种情况成立。但这一结果过于违反直觉，以至于在大多数实际应用中毫无用处。通常更好的做法是避免对复杂多边形使用“内部性”这一概念。

多边形分类。我们现在可以将前面介绍的多个思想结合起来，编写一个函数，用于对任意多边形进行分类：判断它是简单多边形还是复杂多边形；如果是简单多边形，则进一步判断它是凸的还是凹的，以及它是逆时针方向（CCW，总环绕数为1）还是顺时针方向（CW，总环绕数为$-1$）。

// polygon.h

Int ispolysimple(const vector<Point<2>>& vt) {
    // 根据顶点向量 vt 对多边形进行分类。
    // 若多边形为复杂多边形（存在相交边），返回0。
    // 若为简单凸多边形，返回±1。
    // 若为简单凹多边形，返回±2。
    // 返回值的符号表示多边形方向：正号为CCW，负号为CW。
    Int i, ii, j, jj, np, schg = 0, wind = 0;
    Doub p0, p1, d0, d1, pp0, pp1, dd0, dd1, t, tp, t1, t2, crs, crsp = 0.0;
    np = vt.size();
    p0 = vt[0].x[0] - vt[np - 1].x[0];
    p1 = vt[0].x[1] - vt[np - 1].x[1];
    for (i = 0, ii = 1; i < np; i++, ii++) {
        if (ii == np) ii = 0;
        d0 = vt[ii].x[0] - vt[i].x[0];
        d1 = vt[ii].x[1] - vt[i].x[1];
        crs = p0 * d1 - p1 * d0;
        if (crs * crsp < 0) schg = 1;
        if (p1 <= 0.0) {
            if (d1 > 0.0 && crs > 0.0) wind++;
        } else {
            if (d1 <= 0.0 && crs < 0.0) wind--;
        }
        p0 = d0;
        p1 = d1;
        if (crs != 0.0) crsp = crs; // 仅当叉积有符号时才保存前一次的叉积！
    }

    if (abs(wind) != 1) return 0;
    if (schg == 0) return (wind > 0 ? 1 : -1); // 多边形为简单且凸。

    // 唉，所有快速判断方法都已用尽，现在必须检查所有边对是否存在交点：
    for (i = 0, ii = 1; i < np; i++, ii++) {
        if (ii == np) ii = 0;
        d0 = vt[i].x[0];
        d1 = vt[i].x[1];
        p0 = vt[ii].x[0];
        p1 = vt[ii].x[1];
        tp = 0.0;
        for (j = i + 1, jj = i + 2; j < np; j++, jj++) {
            if (jj == np) {
                if (i == 0) break;
                jj = 0;
            }
            dd0 = vt[jj].x[0];
            dd1 = vt[jj].x[1];
            t = (dd0 - d0) * (p1 - d1) - (dd1 - d1) * (p0 - d0);
            if (t * tp <= 0.0 && j > i + 1) {
                // 第一次循环仅用于计算初始的tp。
                pp0 = vt[j].x[0];
                pp1 = vt[j].x[1];
                t1 = (p0 - dd0) * (pp1 - dd1) - (p1 - dd1) * (pp0 - dd0);
                t2 = (d0 - dd0) * (pp1 - dd1) - (d1 - dd1) * (pp0 - dd0);
                if (t1 * t2 <= 0.0) return 0; // 发现交点，直接返回。
            }
            tp = t;
        }
    }
    return (wind > 0 ? 2 : -2); // 未发现交点，为简单凹多边形。
}

当ispolysimple发现快速判断指标不足以得出结论，必须检查所有边对是否存在交点时，它采用的是显而易见的$O(N^2)$双重循环方法。对于较小的$N$（例如小于10），这种方法可能与其他策略一样快。然而，如果你需要处理大量顶点数较大的多边形，则应替换为在$N$上具有更好扩展性的方法。一种可行方案是利用§21.8中的代码，定义一个具有collides()方法的线段类，然后逐个将线段插入QO树中，并在每一步检查是否存在碰撞。（注意：简单多边形中相邻的边允许在其共享顶点处“碰撞”。）

多边形的面积。接下来我们讨论多边形的面积。多边形的（有符号）面积定义为：其各个区域的面积乘以该区域的环绕数后的总和。对于简单多边形，面积在几何上符合直观预期，只是当多边形按顺时针（CW）方向遍历时，面积符号为负（而逆时针CCW方向则为正）。（我们之前在三角形的特例中已见过这一点。）而对于如图21.4.5所示的复杂多边形，结果则较难直观理解（通常也较无用），因为某些区域（例如环绕数为0的内部区域）完全不计入面积，而其他区域则可能被重复计算（本例中为两次）。

然而，这种面积定义的一大优势在于，它导出了一个适用于简单和复杂多边形的统一简洁表达式。设$x_i$和$y_i$分别为多边形顶点${\mathbf{p}}_i$的0坐标和1坐标，$\mathcal{A}$为多边形的面积，则有以下三种等价形式：

$$2\mathcal{A}=\sum _{i=0}^{N-1}{x}_i{y}_{i+1}-x_{i+1}{y}_i$$

$$\begin{array}{rl}& =\sum _{i=0}^{N-1}(x_{i+1}+x_i)(y_{i+1}-y_i)\\ & =\sum _{i=0}^{N-1}{x}_i\left(y_{i+1}-y_{i-1}\right)\end{array}$$

计算上述任一形式只需对多边形顶点进行一次循环。（这些公式最早可追溯至1769年的Meister和1795年的Gauss。）

虽然我们不会详细推导公式（21.4.20），但其中间形式具有直观的几何解释：它计算的是若干梯形的面积之和，每个梯形有两个顶点位于y轴（$x=0$）上，纵坐标分别为$y_i$和$y_{i+1}$，另外两个顶点则是多边形上对应纵坐标的点。在绕行多边形一周的过程中，负面积的梯形会抵消正面积的梯形，最终仅保留多边形内部的净面积。

有趣的是，任意多边形的质心（或称重心）的$x$和$y$坐标也有非常类似的公式[3]：

$$\begin{array}{r}\overline{x}=\frac{1}{6}{\sum }_{i=0}^{N-1}(x_{i+1}+x_i)(x_i{y}_{i+1}-x_{i+1}{y}_i)\\ \overline{y}=\frac{1}{6}{\sum }_{i=0}^{N-1}(y_{i+1}+y_i)(x_i{y}_{i+1}-x_{i+1}{y}_i)\end{array}$$

注意这些公式与（21.4.20）式中的公共子表达式，因此同时计算面积和质心位置是高效的。

最后，再提供两个关于多边形的趣闻，供你增长见识或娱乐：

• 若两个简单多边形面积相等，则第一个多边形可被切割成有限个直边多边形碎片，并重新拼合成第二个多边形。这被称为Bolyai-Gerwien定理。（三维空间中对应的多面体命题——“希尔伯特第三问题”——已于1900年被Dehn证明为错误。）

• 具有$N$条边的正多边形可用圆规和直尺构造，当且仅当$N$的质因数分解仅包含2、3、5、17、257和65537（其中奇数因子均为费马素数），且每个奇数因子至多出现一次。目前尚不清楚是否存在其他可构造的正$N$边形；但若存在，则其$N$必包含一个不小于$2^{2^{33}}+1$的因子。目前已知费马素数的乘积（即目前已知边数最多的可构造奇数边正多边形）为$2^{32}-1=4294967295$，这个数在计算机领域广为人知，是最大的32位正整数。真是耐人寻味。

参考文献

de Berg, M., van Kreveld, M., Overmars, M., and Schwarzkopf, O. 2000, Computational Geometry: Algorithms and Applications, 2nd revised ed. (Berlin: Springer), Chapter 2.

O'Rourke, J. 1998, Computational Geometry in C, 2nd ed. (Cambridge, UK: Cambridge University Press), §7.4.

Goldman, R. 1990, "Intersection of Two Lines in Three-Space," in Graphics Gems, Glassner, A.S., ed. (San Diego: Academic Press).[2]

Bashein, G. and Detmer, P.R. 1994, "Centroid of a Polygon," in Graphics Gems IV, Heckbert, P.S., ed. (Cambridge, MA: Academic Press).[3]

Sunday, D. 2007+, at http://softsurfer.com/algorithm_archive.htm.[4]

Haines, E. 1994, "Point in Polygon Strategies," in Graphics Gems IV, Heckbert, P.S., ed. (Cambridge, MA: Academic Press).[5]

Wikipedia 2007+, "Polygon," at http://en.wikipedia.org.

21.5 球面与旋转

拓扑学家将地球的表面称为 2-球面，而几何学家则称之为 3-球面；因此术语“$n$-球面”有些模糊。为避免歧义，我们将使用“$n$ 维空间中的球面”这一说法。（对于地球，$n=3$。）“球面”指表面，“球体”指内部体积。

以原点为中心、半径为 $r$ 的 $n$ 维球面是满足以下条件的点的轨迹：

$$x_0^2+\cdots +x_{n-1}^2=r^2$$

$n$ 维球面上的点可以用 $n-1$ 个角坐标来指定，大致类似于三维球面上的纬度和经度：

$$\begin{array}{rl}& x_0=r\cos {\psi }_0\\ & x_1=r\sin {\psi }_0\cos {\psi }_1\\ & \cdots \\ & x_{n-2}=r\sin {\psi }_0\sin {\psi }_1\cdots \cos {\psi }_{n-2}\\ & x_{n-1}=r\sin {\psi }_0\sin {\psi }_1\cdots \sin {\psi }_{n-2}\end{array}$$

除最后一个角外，其余所有角的取值范围为

$$0<{\psi }_i<\pi ,i=0,\dots ,n-3$$

即类似于“纬度”。最后一个角类似于“经度”，

$$0\le {\psi }_{n-2}\le 2\pi$$

$n$ 维球面的表面积 $S_n$ 满足一个简单的递推关系：

$$\begin{array}{rlr}& & (\mathrm{两个点})\\ & & S_2=2\pi r\\ & & S_n=\frac{2\pi r^2}{n-2}{S}_{n-2},n>2\end{array}$$

$n$ 维球体的体积 $V_n$ 等于 $r/n$ 乘以包围它的 $n$ 维球面的面积，同样具有一个简单的递推关系：

$$\begin{array}{rlr}& & (\mathrm{线段长度})\\ & & V_1=2r\\ & & V_2=\pi r^2\end{array}(\mathrm{圆的面积})$$

$$V_n=\frac{r}{n}{S}_n=\frac{2\pi r^2}{n}{V}_{n-2}$$

闭式表达式需要用到伽马函数：

$$\begin{array}{r}{S}_n=\frac{2{\pi }^{n/2}}{\Gamma (\frac{1}{2}n)}{r}^{n-1}\\ V_n=\frac{2{\pi }^{n/2}}{n\Gamma (\frac{1}{2}n)}{r}^n\end{array}$$

当 $n$ 变得很大时，球体体积与外接（超）立方体体积的比值迅速趋近于零：

$$\frac{V_n}{{\gamma }^n}\to 0,n\to \infty$$

21.5.1 在球面上随机选取一点

你不能通过在公式 (21.5.2) 中为 $n-1$ 个角度均匀随机地选取值来获得 $n$ 维球面上的一个随机点，正如你不能通过向墨卡托投影地图（或其他任何非等面积投影）上投掷飞镖来获得地球表面上的一个随机点一样。

一种优雅的通用方法是生成 $n$ 个独立同分布的零均值正态（高斯）偏差量，记为 $y_0,\dots ,y_{n-1}$（参见 §7.3），然后通过下式计算 $n$ 维单位球面上的一点 $\mathbf{x}$：

$$\mathbf{x}=\frac{\mathbf{y}}{|\mathbf{y}|}$$

换句话说，

$$x_i=y_i/\sqrt{\sum _{j=0}^{n-1}{y}_j^2}$$

这种方法之所以有效，是因为 $n$ 维空间中球对称的高斯分布可以自然地分解为独立的一维高斯分布的乘积。如果你想要球体内部的一个随机点，则再生成一个在 $[0,1]$ 上均匀分布的随机偏差量 $u$，并按如下方式计算该点的坐标：

$$x_i=u^{1/n}{y}_i/\sqrt{\sum _{j=0}^{n-1}{y}_j^2}$$

当然，你可以按比例缩放至任意其他半径的球面。

对于二维、三维和四维球面，还有更快的专用方法。对于二维情形（即圆），在 $[-1,1]$ 中均匀选取 $u_0$ 和 $u_1$，若 $u_0^2+u_1^2>1$ 则拒绝该选择。这样可得到单位圆内的一个随机点。然后按如下方式缩放，即可得到圆周上的点：

$$x_0=\frac{u_0}{\sqrt{u_0^2+u_1^2}},x_1=\frac{u_1}{\sqrt{u_0^2+u_1^2}}$$

（我们已在 §7.3 中讨论过此方法，当时是在柯西偏差量的背景下。）

一种适用于三维空间的更快方法（同样仅使用两个随机数）由 Marsaglia 提出 [1]。如前所述，在单位圆内选取一点 $(u_0,u_1)$。那么三维球面上的一个随机点为：

$$\begin{array}{r}{x}_0=2u_0\sqrt{1-u_0^2-u_1^2}\\ x_1=2u_1\sqrt{1-u_0^2-u_1^2}\\ x_2=1-2(u_0^2+u_1^2)\end{array}$$

对于四维球面，如上所述，选取两个单位圆内的独立点 $(u_0,u_1)$ 和 $(u_2,u_3)$。那么四维球面上的一个随机点为 [1]：

$$\begin{array}{rl}& x_0=u_0\\ & x_1=u_1\\ & x_2=u_2\sqrt{\frac{1-u_0^2-u_1^2}{u_2^2+u_3^2}}\\ & x_3=u_3\sqrt{\frac{1-u_0^2-u_1^2}{u_2^2+u_3^2}}\end{array}$$

遗憾的是，目前尚无已知的推广方法适用于更高维的情形。

21.5.2 生成一个随机旋转矩阵

不要将此与在球面上选取一个点混淆。$n$ 维空间中的旋转矩阵 $\mathbf{M}$ 是一个正交的 $n\times n$ 矩阵。对于一个真旋转（proper rotation），$\mathbf{M}$ 的行列式必须为 1。另一种可能性是行列式为 $-1$，这表示一个非真旋转（improper rotation），可分解为一个真旋转后接一个反射。旋转矩阵 $\mathbf{M}$ 通过下式将任意点 $\mathbf{x}$ 映射到新点 ${\mathbf{x}}^{\prime }$：

$${\mathbf{x}}^{\prime }=\mathbf{M}\cdot \mathbf{x}$$

生成均匀随机旋转矩阵的一般方法是：构造一个 $n\times n$ 的矩阵 $\mathbf{G}$，其元素为独立同分布的零均值正态（高斯）随机数。然后，使用 §2.10 中的 QRdcmp 对 $\mathbf{G}$ 进行 QR 分解，即 $\mathbf{G}=\mathbf{Q}\cdot \mathbf{R}$。除了可能行列式符号错误外，矩阵 $\mathbf{Q}$ 此时即为一个均匀随机的旋转矩阵。QRdcmp 中使用的方法是应用 $n-1$ 个 Householder 变换，每个变换都是一个行列式为 $-1$ 的反射。因此，为了得到行列式为 1 的矩阵，当 $n$ 为奇数时，我们对 $\mathbf{Q}$ 不做任何处理；当 $n$ 为偶数时，只需交换 $\mathbf{Q}$ 中任意两行即可得到最终结果。

对于较大的 $n$，该分解的计算复杂度为 $O(n^3)$，可能较为耗时。若需更快但更复杂的方法，参见 [2,3]。

对于二维和三维情形，存在更快的专用方法。二维随机旋转矩阵的元素是某个随机角度 $\theta \in [0,2\pi ]$ 的正弦和余弦：

$$\left(\begin{array}{ll}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right)$$

我们可以通过 (21.5.12) 在单位圆上生成一个随机点，然后令 $\cos \theta =x_0$、$\sin \theta =x_1$，从而避免调用三角函数。

对于三维情形，一种快速方法是利用公式 (21.5.14) 生成四维球面上的一个随机点，然后构造如下 $3\times 3$ 正交矩阵：

$$\begin{array}{r}\left[\begin{array}{lll}1-2(x_1^2+x_2^2)& 2(x_0{x}_1-x_3{x}_2)& 2(x_0{x}_2+x_3{x}_1)\\ 2(x_0{x}_1+x_3{x}_2)& 1-2(x_0^2+x_2^2)& 2(x_1{x}_2-x_3{x}_0)\\ 2(x_0{x}_2-x_3{x}_1)& 2(x_1{x}_2+x_3{x}_0)& 1-2(x_0^2+x_1^2)\end{array}\right]\end{array}$$

该矩阵在所有旋转中是均匀随机的 [4,5]。

参考文献

Marsaglia, G. 1972, "Choosing a Point from the Surface of a Sphere," Annals of Mathematical Statistics, vol. 43, pp. 645–646.[1]

Genz, A. 2000, "Methods for Generating Random Orthogonal Matrices," in Monte Carlo and Quasi-Monte Carlo Methods, Proceedings of the Third International Conference on Monte Carlo and Quasi-Monte Carlo Methods in Scientific Computing (MCQMC98) (Berlin: Springer).[2]

Anderson, T.W., Olkin, I., and Underhill, L.G. 1987, "Generation of Random Orthogonal Matrices," SIAM Journal on Scientific and Statistical Computing, vol. 8, pp. 625–629.[3]

Shoemake, K. 1985, "Animating Rotation with Quaternion Curves," Computer Graphics, Proceedings of SIGGRAPH 1985, vol. 19, pp. 245–254.[4]

Shoemake, K. 1992, "Uniform Random Rotations," in Graphics Gems III, Kirk, D., ed. (Cambridge, MA: Academic Press), pp. 124–132.[5]

21.6 三角剖分与 Delaunay 三角剖分

我们可以非正式地定义平面上 $N$ 个点的三角剖分如下：尽可能多地用直线段连接给定的点，但不允许任意两条线段相交。当你无法再连接更多线段时，就得到了一个三角剖分。显然，给定点集存在多种三角剖分方式。图 21.6.1 展示了同一组 50 个点的三种三角剖分。其中两种是“随机”的，基本遵循了上述非正式定义；第三种是一种非常特殊的三角剖分，称为 Delaunay 三角剖分。从下文将更精确阐述的意义上说，Delaunay 三角剖分的三角形能最好地避免出现小角度和长边。

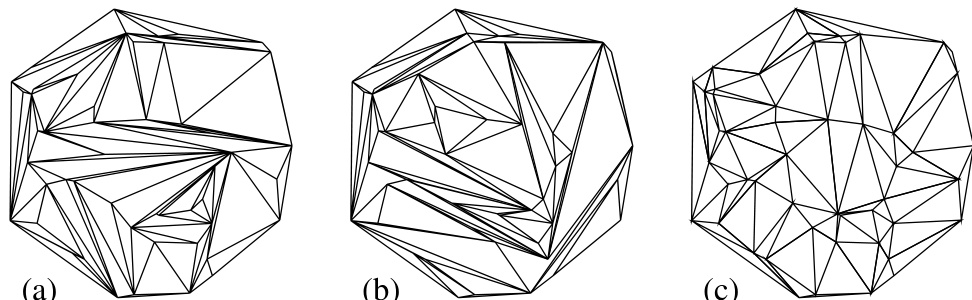
图 21.6.1. 同一组 50 个随机点的三种三角剖分：(a) 和 (b) 是“差的”（随机）三角剖分，而 (c) 是“好的”（Delaunay）三角剖分。每种情形下的线段数和三角形数均相同。

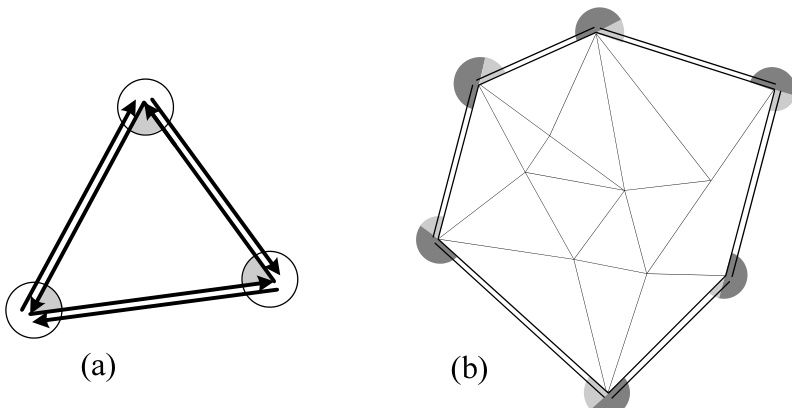
图 21.6.2. 如何计算三角剖分中的线段数和三角形数。(a) 每个三角形“消耗” $1/2$ 个点和 $3/2$ 条线段。(b) 凸包上的 $n$ 个点“消耗” $n/2+1$ 个点和 $n/2$ 条线段。

给定点集的所有三角剖分都具有相同的外边界，称为该点集的凸包。从三角剖分的定义可以非正式地看出这一点：凸包边界上的线段（边）不会与任何其他实际或潜在的内部边发生冲突，因此在达到停止条件前总会被加入。凸包中的点数 $n$（以及边数）至少为 3，最多可达 $N$，例如当所有点都位于一个圆上时。（此处及下文，我们将忽略“所有点共线”等退化情形。）

或许令人惊讶的是，给定点集的所有三角剖分具有相同数量的线段（$L$）和三角形（$T$），其具体关系为：

$$\begin{array}{r}L=3N-n-3\\ T=2N-n-2\end{array}$$

高斯所知的这一证明，若参考图21.6.2，则非常简单。由于三角形的内角和为 $\pi$ 弧度，每个三角形“消耗”了相当于半个点的角量。将每条线视为两条半射线（代表顺时针三角形中两种可能的遍历方向）是有帮助的。于是，每个三角形消耗三条半射线。我们还需单独考虑凸包上的顶点，如下所述：每个这样的点自身就消耗 $\pi$ 弧度（图中深色阴影角），再加上绕凸包一周时（浅色阴影外角之和）额外消耗的 $2\pi$ 弧度。

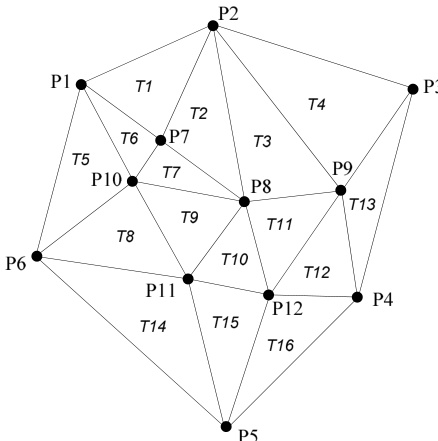
图21.6.3. 一个三角剖分的例子，其中 $N=12$，$n=6$，$T=16$，$L=27$，这些值满足方程 (21.6.1)。

这些考虑给出了以下关系式：

$$\begin{array}{rlr}& 2\pi N=\pi T+\pi n+2\pi & (\mathrm{弧度计数})\\ & 2L=3T+n& (\mathrm{半射线计数})\end{array}$$

可重新整理得到方程 (21.6.1)。图21.6.3展示了图21.6.2(b)的三角剖分，并对其点和三角形进行了编号。

21.6.1 Delaunay 三角剖分

俄罗斯数学家 Boris Nikolaevich Delone（1890–1980），同时也以攀岩者身份闻名，于1934年首次发表了 Delaunay 三角剖分背后的思想。由于他的论文以法语撰写，其姓名被转写成法语发音（近似正确）的形式。在英语中更合适的发音可能是“dyeh-LOAN-yeh”。

Delaunay 三角剖分具有许多非凡的性质，并可通过多种抽象方式定义。然而，我们将采用一个非常具体的性质作为定义，如图21.6.4所示。考虑所有三角剖分，其中四个点 $A$、$B$、$C$、$D$ 构成两个背靠背的三角形。此时，可通过删除公共边（图中为 $BD$）并替换为四边形的另一条对角线（图中为 $AC$）来得到另一种三角剖分。Delaunay 三角剖分定义为：总是选择使两个三角形六个内角中的最小角最大的那条对角线。因此，图中所示的边 $BD$ 对 Delaunay 三角剖分而言是非法的，而 $AC$ 被称为合法的。将三角剖分从非法边转换为合法边的过程称为边翻转（edge flip）。当任意两个三角形共享一条边时，恰好有一种配置（原始或翻转后）是合法的（除非四个点共圆，此时两者均合法）。

这种“最大最小角”性质在几何上等价于关于点 $A,B,C,D$ 的其他陈述。其中一种陈述是：非法三角形（如图(a)中的 $ABD$ 或 $BCD$）的外接圆必定包含另一个点（分别为 $C$ 或 $A$）。而对于合法三角形（如图(b)所示），这种情况永远不会发生。我们可以以此作为起点证明以下定理：

• Delaunay 三角剖分中任意三角形的外接圆内不包含其他顶点。

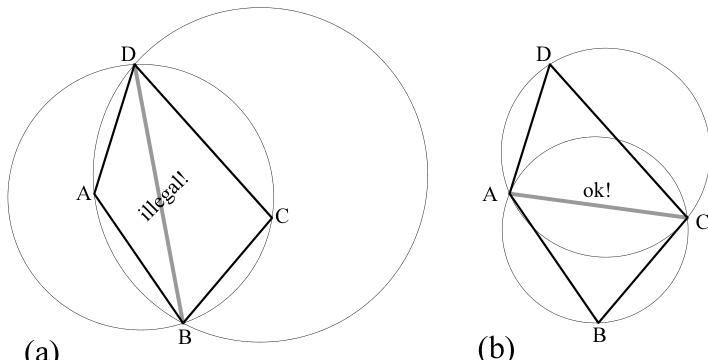
图21.6.4. Delaunay 三角剖分可定义为：背靠背的两个三角形在公共边翻转为另一条对角线时，其最小角总是更大。等价地，任意三角形的外接圆不包含其他顶点。所谓的边翻转将图(a)转换为图(b)。

尽管“最大最小角”性质是局部定义的（每次仅针对一个四边形），但它可推出一个非凡的全局定理：

• 在所有点集的三角剖分中，Delaunay 三角剖分具有最大的最小角。此处“最大”定义为：将所有角度从小到大排序后，按字典序与任何其他三角剖分的角度序列进行比较。字典序比较的含义是：首先比较最小角；若已分出胜负，则停止；若最小角相等，则比较次小角，依此类推。

另一个定理是：

• 两个顶点由一条 Delaunay 边连接，当且仅当存在一个圆，包含这两个顶点且不包含其他顶点。

若点集处于一般位置（即任意三点不共线，任意四点不共圆），则 Delaunay 三角剖分存在且唯一；任何构造方法都将得到完全相同的三角形集合。

你可能会疑惑 Delaunay 三角剖分是否也是最小权三角剖分（即总边长最小的三角剖分）。一般而言，答案是否定的。尽管最小权三角剖分在某些应用中可能有用，但目前甚至尚不清楚能否在低于指数时间（随 $N$ 增长）内构造它。而 Delaunay 构造则很快，时间复杂度为 $O(N\log N)$。因此，实践中我们通常采用 Delaunay！

那么，如何构造 Delaunay 三角剖分呢？从概念上讲，我们可以从任意三角剖分开始，只要存在非法边，就通过边翻转不断消除，直到无法再翻转为止。由于（i）每次翻转都会改变并增加角度列表的字典序，且（ii）可能的三角剖分数量有限，该过程必在有限次翻转后终止于一个 Delaunay 三角剖分。尽管如上所述的方法效率不高，但可轻易改进为一种高效算法，即所谓的随机增量算法 [1]。

我们现在实现的算法是“增量式”的，即逐个向三角剖分中添加点，并在每个阶段保持 Delaunay 性质。它也是“随机化”的，因为点以随机顺序添加。事实证明，这种随机化（几乎）保证了算法的期望时间为 $O(N\log N)$。（若无随机化，则可能遇到病态情况，导致

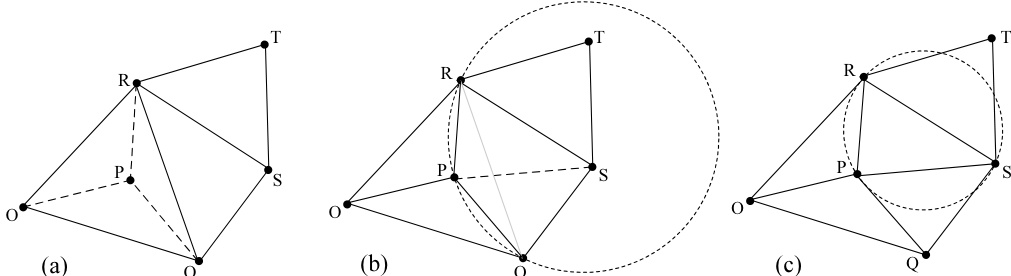
图21.6.5. 向 Delaunay 三角剖分中插入新点的步骤。(a) 将新点 $P$ 连接到包围三角形的顶点。(b) 检查包围三角形是否存在非法边（此处将 $QR$ 替换为 $PS$）。(c) 递归检查所有以 $P$ 为顶点的新生成三角形。（此处 $RS$ 是合法的，故终止。）$O(N^2)$ 的运行时间。）

图21.6.5展示了向现有三角形内部添加新点 $P$ 的过程。首先，将其连接到包围三角形的顶点，从而生成三个新三角形。（我们排除了 $P$ 恰好位于现有边上的特殊情况，下文将详述。）接着，检查这三个新三角形中与 $P$ 相对的边是否合法。若非法，则进行边翻转。每次边翻转会生成两个以 $P$ 为顶点的新三角形，因此又有两条与 $P$ 相对的新边需要检查合法性。该过程是递归的，但不会远离 $P$。这是关键点：插入点 $P$ 后，唯一可能变为非法的边，是那些包含 $P$ 的三角形中与 $P$ 相对的边。算法 $O(N\log N)$ 时间复杂度的证明正是基于这一事实，并利用类似方程 (21.6.1) 的关系对 $P$ 所在三角形的平均数量进行界定。（证明细节见 [2]。）

由于目前我们仅知道如何添加位于三角剖分内部的点 $P$，那么如何开始呢？一种简便方法是向点集中添加三个“虚拟”点，构成一个足够大的初始三角形，以包围后续添加的所有“真实”点。最后，移除这些虚拟点及其所有连接边。严格来说，这些虚拟点应被视为位于无穷远处（因此代码中每次引用它们时都需要特殊逻辑）。若其距离仅为有限值，则构造的三角剖分可能“不完全”满足 Delaunay 性质。例如，在某些异常情况下，其外边界（凸包）可能略微凹陷，产生微小的负角度，其量级约为“真实”点集直径与到“虚拟”点距离的比值。

以上已提供足够的一般性信息，接下来进入具体细节。

21.6.2 实现细节

由于大多数读者会跳过标题为“实现细节”的章节，此处正好坦白我们在 Delaunay 实现中使用的几个“小技巧”，目的是使代码及其解释保持在可管理的长度内。若你需要一个无此类技巧的、坚如磐石的 Delaunay 代码，通过网络搜索可找到多个免费可用的实现。我们的代码简短且快速，适用于预期用途；但在两方面是近似的：首先，我们并未将初始包围三角形置于无穷远处（如前所述的“圣洁”建议），而是将其置于距离约 bigscale（一个可调参数，默认值为1000）处，该距离以点集包围盒尺寸为单位。其次，我们未处理前述的特殊情况，即待添加点恰好落在现有边上（或在舍入误差容限内落在边上）。对于一般位置的点，这种情况“永不”发生；但在现实中却“总是”发生，因为用户总爱尝试规则排列的测试点！当我们检测到此问题时，会将问题点的位置随机扰动一个微小量 fuzz（另一个可调参数，默认值为 $10^{-6}$），该量以包围盒尺寸为单位。

一个尚未讨论但非常重要的实现细节是：如何快速找到新点所在的现有三角形。从概念上讲，我们可以将三角形放入 QO 树（$\S$21.8），但这无法使我们的算法达到期望的 $O(N\log N)$ 性能。文献中已确立的更好方案是：维护一个树结构，记录构造过程中曾存在过的每个三角形的所有后代。具体而言，从巨大的“根”三角形开始，每当一个三角形被细分为三个新三角形时，我们设置指向其三个子三角形的指针。当边翻转导致两个三角形消失并生成两个新三角形时，我们将新三角形设为两个消失三角形的子代（尽管每个消失三角形仅包含每个新三角形的一部分）。在此方案中，每个三角形最多有两个或三个子代，因此我们可以显式预留指针空间（即无需可扩展的链表）。

借助此结构，可在现有三角剖分中快速定位一个点：从根三角形开始，递归选择包含该点的子三角形。当到达树的叶节点时，即找到当前三角剖分中包含该点的三角形。因此，我们需要一个“三角形元素”（Triel）结构：

struct Triel {
    // 用于三角形后代树中的元素结构，每个元素最多有三个子代
    Point<2> *pts;
    Int p[3];
    Int d[3];
    Int stat;
    void setme(Int a, Int b, Int c, Point<2> *ptss) {
        // 设置 Triel 的数据
        pts = ptss;
        p[0] = a; p[1] = b; p[2] = c;
        d[0] = d[1] = d[2] = -1;
        stat = 1;
    }
    Int contains(Point<2> point) {
        // 若点在三角形内返回1，若在边界上返回0，若在外部返回-1。（假设为逆时针三角形。）
        Doub d;
        Int i, j, ztest = 0;
        for (i = 0; i < 3; i++) {
            j = (i + 1) % 3;
            d = (pts[p[j]].x[0] - pts[p[i]].x[0]) * (point.x[1] - pts[p[i]].x[1]) 
                - (pts[p[j]].x[1] - pts[p[i]].x[1]) * (point.x[0] - pts[p[i]].x[0]);
            if (d < 0.0) return -1;
            if (d == 0.0) ztest = 1;
        }
        return (ztest ? 0 : 1);
    }
};

我们在开始时创建一个足够大的 Triel 数组，并使用整数来指向数组元素。我们在 Triel 中省略了任何显式的构造函数或赋值运算符，因为在此用途中不需要它们。如果你以其他方式使用 Triel，请务必添加这些函数。

我们需要另外两种快速查找方法：(1) 给定三角形中的一个点及其对边，找出四边形中的第四个点，即位于给定边另一侧的点（如果存在）；(2) 给定三个点，在 Triel 元素数组中查找其三角形的索引（如果存在）。我们的策略是为这两个功能分别使用哈希表（称为 linehash 和 trihash）。具体来说，每当创建一个三角形（始终为逆时针方向）且顶点为 $A$、$B$、$C$ 时，我们会在一个特殊构造的键下存储指向每个点的索引：

$$\mathrm{linehash}(h(B)-h(C))\leftarrow A(\mathrm{et}cyc.)$$

其中函数 $h$ 是一个 64 位哈希函数，“et cyc.” 表示对 $A,B,C$ 的另外两个循环排列执行相同的操作。这里的技巧是，如果我们想找到边 $BC$ 另一侧的点，只需在哈希表中查找键 $h(C)-h(B)$（即公式 21.6.3 中键的“负值”）。类似地，存储和检索 Triel 的技巧是：当我们在存储数组的位置 $j$ 处创建一个 Triel 时，设置

$$\mathrm{trihash}(h(A)\hat{}h(B)\hat{}h(C))\leftarrow j$$

其中 $\hat{}$ 表示异或（XOR）操作。由于该键在 $A$、$B$、$C$ 中是对称的，因此我们可以以任意顺序知道三角形的顶点并找到该三角形。

由于我们“手动”计算哈希键，我们可以指示两个哈希表使用空（因此快速）的哈希函数。此外，还有一个用于判断某点是否位于另外三点外接圆内的工具函数。以下是这两个代码片段：

Doub incircle(Point<2> d, Point<2> a, Point<2> b, Point<2> c) {
    // 若点 d 分别位于通过 a、b、c 三点的圆内、圆上或圆外，则返回正值、零或负值。
    Circle cc = circumcircle(a, b, c); // §21.3 中定义的例程。
    Doub radd = SQR(d.x[0] - cc.center.x[0]) + SQR(d.x[1] - cc.center.x[1]);
    return (SQR(cc.radius) - radd);
}

struct Nullhash {
    // 空哈希函数。使用键（假设已哈希）作为其自身的哈希值。
    Nullhash(Int nn) {}
    inline Ullong fn(const void *key) const { return *((Ullong *)key); }
};

在声明 Delaunay 结构之前，以上就是我们需要的所有准备工作。

struct Delaunay {
    // 用于从给定点集构造 Delaunay 三角剖分的结构。
    Int npts, ntri, ntree, ntremax, opt; // 点数、三角形数、Triel 列表中的元素数及其最大值、包围盒的尺寸。
    vector<Triel> thelist;
    Hash<Ullong, Int, Nullhash> *linehash; // 使用空哈希函数创建哈希表。
    Hash<Ullong, Int, Nullhash> *trihash;
    Int *perm;
    Delaunay(vector<Point<2>> &pvec, Int options = 0);
    // 从点向量构造 Delaunay 三角剖分。变量 options 供某些应用程序使用。
    Ranhash hashfn;
    Doub interpolate(const Point<2> &p, const vector<Doub> &fnvals, Doub defaultval = 0.0);
    // 接下来的四个函数将在下文详细解释。
    void insertapoint(Int r);
    Int whichcontainspt(const Point<2> &p, Int strict = 0);
    Int storetriangle(Int a, Int b, Int c);
    void erasetriangle(Int a, Int b, Int c);
    static Unt jran;
    static const Doub fuzz, bigscale;
};
const Doub Delaunay::fuzz = 1.0e-6;
const Doub Delaunay::bigscale = 1000.0;
Unt Delaunay::jran = 14921620; // 如需调整，请参见正文。

变量 jran 与哈希函数结合使用，作为一个便捷的随机数生成器。函数 interpolate() 用于在非结构化网格上插值函数，将在 §21.7 中讨论。其余内容将在后续过程中变得清晰。

操作从构造函数开始。我们计算点集的包围盒，构造并存储包含这些点的“巨大”根三角形，生成一个随机排列作为添加点的顺序，然后（进行实际工作）依次对每个点调用 insertapoint() 函数。之后仅需进行一些清理工作。

Delaunay::Delaunay(vector<Point<2>> &pvec, Int options)
    : npts(pvec.size()), ntri(0), ntree(0), ntremax(10 * npts + 1000), opt(options), pts(npts + 3), thelist(ntremax) {
    // 从点向量 pvec 构造 Delaunay 三角剖分。
    // 如果 options 的第 0 位非零，则删除构造中使用的哈希表（某些应用程序可能希望保留它们并将 options 设为 1）。
    Int j;
    Doub xl, xh, yl, yh;
    linehash = new Hash<Ullong, Int, Nullhash>(6 * npts + 12, 6 * npts + 12);
    trihash = new Hash<Ullong, Int, Nullhash>(2 * npts + 6, 2 * npts + 6);
    perm = new Int[npts]; // 用于随机化点顺序的排列。
    xl = xh = pvec[0].x[0];
    yl = yh = pvec[0].x[1];
    for (j = 0; j < npts; j++) {
        pts[j] = pvec[j];
        perm[j] = j;
        if (pvec[j].x[0] < xl) xl = pvec[j].x[0];
        if (pvec[j].x[0] > xh) xh = pvec[j].x[0];
        if (pvec[j].x[1] < yl) yl = pvec[j].x[1];
        if (pvec[j].x[1] > yh) yh = pvec[j].x[1];
    }
    Doub delx = xh - xl;
    Doub dely = yh - yl;
    pts[npts] = Point<2>(0.5 * (xl + xh), yh + bigscale * dely);
    pts[npts + 1] = Point<2>(xl - 0.5 * bigscale * delx, yl - 0.5 * bigscale * dely);
    pts[npts + 2] = Point<2>(xh + 0.5 * bigscale * delx, yl - 0.5 * bigscale * dely);
    storetriangle(npts, npts + 1, npts + 2); // 创建根三角形。
    // 创建随机排列：
    for (j = npts; j > 0; j--) {
        SWAP(perm[j - 1], perm[hashfn.int64(jran++) % j]);
    }
    for (j = 0; j < npts; j++) {
        insertapoint(perm[j]); // 所有实际工作都在这里！
    }
    // 清理：移除包含虚拟点的三角形。
    for (j = 0; j < ntree; j++) {
        if (thelist[j].stat > 0) {
            if (thelist[j].p[0] >= npts || thelist[j].p[1] >= npts || thelist[j].p[2] >= npts) {
                thelist[j].stat = -1;
                ntri--;
            }
        }
    }
    if (!(opt & 1)) {
        delete[] perm;
        delete trihash;
        delete linehash;
    }
}

如前所述，算法的核心在 insertapoint() 中。我们首先定位包含新点的三角形（此处失败仅意味着该点位于现有边上，此时我们如前所述对点位置进行微小扰动后重试）。接着存储三个新三角形并删除旧三角形。然后定位并修复所有非法边，通过一个简单的后进先出栈来递归处理待检查的边。

void Delaunay::insertapoint(Int r) {
    // 将索引为 r 的点增量式地添加到 Delaunay 三角剖分中。
    Int i, j, k, l, s, tno, ntask, d0, d1, d2;
    Ullong key;
    Int tasks[50], taski[50], taskj[50];
    for (j = 0; j < 3; j++) {
        tno = whichcontainspt(pts[r], 1);
        if (tno >= 0) break; // 找到包含点的三角形。
        // 对点位置进行微小扰动。
        pts[r].x[0] += fuzz * delx * (hashfn.doub(jran++) - 0.5);
        pts[r].x[1] += fuzz * dely * (hashfn.doub(jran++) - 0.5);
    }
    if (j == 3) throw("points degenerate even after fuzzing");
    ntask = 0;
    i = thelist[tno].p[0]; j = thelist[tno].p[1]; k = thelist[tno].p[2];
    // 如果 opt 的第 2 位被设置，则跳过已知在凸包内部的点（用于凸包应用）。
    if (opt & 2 && i < npts && j < npts && k < npts) return;
    d0 = storetriangle(r, i, j); // 创建三个新三角形并加入待检查队列。
    tasks[++ntask] = r; taski[ntask] = i; taskj[ntask] = j;
    d1 = storetriangle(r, j, k);
    tasks[++ntask] = r; taski[ntask] = j; taskj[ntask] = k;
    d2 = storetriangle(r, k, i);
    tasks[++ntask] = r; taski[ntask] = k; taskj[ntask] = i;
    erasetriangle(i, j, k, d0, d1, d2);
    while (ntask) {
        s = tasks[ntask]; i = taski[ntask]; j = taskj[ntask--];
        key = hashfn.int64(j) - hashfn.int64(i); // 查找第四点。
        if (!linehash->get(key, l)) continue;
        if (incircle(pts[l], pts[j], pts[s], pts[i]) > 0.0) { // 需要合法化？
            d0 = storetriangle(s, l, j);
            d1 = storetriangle(s, i, l);
            erasetriangle(s, i, j, d0, d1, -1);
            erasetriangle(l, j, i, d0, d1, -1);
            key = hashfn.int64(i) - hashfn.int64(j);
            linehash->erase(key);
            key = 0 - key;
            linehash->erase(key);
            // 两个新边需要检查：
            tasks[++ntask] = s; taski[ntask] = l; taskj[ntask] = j;
            tasks[++ntask] = s; taski[ntask] = i; taskj[ntask] = l;
        }
    }
}

剩下的部分是用于查找包含某点的三角形以及存储和删除三角形的工具函数。当我们“删除”一个三角形时，实际上只是将其在当前三角剖分中标记为非活动状态，并设置其在后代树中的子三角形（如前所述）。

Int Delaunay::whichcontainspt(const Point<2> &p, Int strict) {
    // 给定点 p，返回三角剖分中包含它的三角形在列表中的索引；失败则返回 -1。
    // 若 strict 非零，则要求严格包含；否则允许点位于边上。
    Int i, j, k = 0;
    while (thelist[k].stat <= 0) {
        for (i = 0; i < 3; i++) {
            if ((j = thelist[k].d[i]) < 0) continue;
            if (strict) {
                if (thelist[j].contains(p) > 0) break;
            } else {
                if (thelist[j].contains(p) >= 0) break;
            }
        }
        if (i == 3) return -1;
        k = j;
    }
    return k; // 正常返回。
}

void Delaunay::erasetriangle(Int a, Int b, Int c, Int d0, Int d1, Int d2) {
    // 在 trihash 中删除三角形 abc，并在 thelist 中将其标记为非活动状态，同时设置其子三角形。
    Ullong key;
    Int j;
    key = hashfn.int64(a) ^ hashfn.int64(b) ^ hashfn.int64(c);
    if (trihash->get(key, j) == 0) throw("nonexistent triangle");
    trihash->erase(key);
    thelist[j].d[0] = d0; thelist[j].d[1] = d1; thelist[j].d[2] = d2;
    thelist[j].stat = 0;
    ntri--;
}

Int Delaunay::storetriangle(Int a, Int b, Int c) {
    // 在 trihash 中存储顶点为 a、b、c 的三角形。
    // 在 linehash 中以对边为键存储其顶点。
    // 将其添加到 thelist 中并返回其索引。
    Ullong key;
    thelist[ntree].setme(a, b, c, &pts[0]);
    key = hashfn.int64(a) ^ hashfn.int64(b) ^ hashfn.int64(c);
    trihash->set(key, ntree);
    key = hashfn.int64(b) - hashfn.int64(c);
    linehash->set(key, a);
    key = hashfn.int64(c) - hashfn.int64(a);
    linehash->set(key, b);
    key = hashfn.int64(a) - hashfn.int64(b);
    linehash->set(key, c);
    if (++ntree == ntremax) throw("thelist is sized too small");
    ntri++;
    return (ntree - 1);
}

你可能会疑惑如何从我们的 Delaunay 结构中获取结果。我们没有提供专门的函数，因为这很大程度上取决于你想如何使用结果。但一般思路是：遍历 thelist[j]（$0\le j<\text{nlist}$）。每个元素都是一个 Triel。如果其 stat 值 $\le 0$，则忽略并继续；如果为 1，则该元素代表最终 Delaunay 三角剖分中的一个三角形。总共有 ntri 个这样的元素。该元素的数组 $\mathbf{p}[\cdot ]$ 包含指向你点向量中三角形三个顶点的整数索引。下一节中的几个例程从 Delaunay 结构中提取点、边或三角形，可作为模板示例。

图 21.6.6 展示了 300 个点的 Delaunay 三角剖分的示例输出。

参考文献

Guibas, L.J., Knuth, D.E., and Sharir, M. 1992, "Randomized Incremental Construction of Delaunay and Voronoi Diagrams," Algorithmica, vol. 7, pp. 381-413.[1]

Lischinski, D. 1994, “增量Delaunay三角剖分”，载于《图形宝典IV》，Heckbert, P.S. 编（马萨诸塞州剑桥：学术出版社）。[展示了使用链式数据结构，而非我们所用的哈希内存。]

de Berg, M., van Kreveld, M., Overmars, M., 与 Schwarzkopf, O. 2000，《计算几何：算法与应用》，第2版修订版（柏林：施普林格出版社），第9章。[2]

O'Rourke, J. 1998，《C语言中的计算几何》，第2版（英国剑桥：剑桥大学出版社），§5.3。

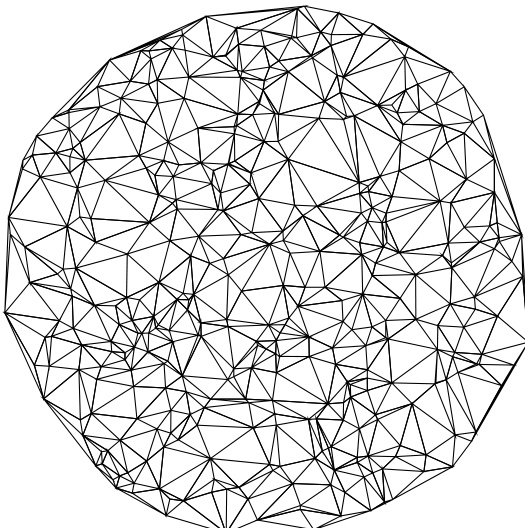
图21.6.6. 本节例程计算的300个在圆内随机选取点的Delaunay三角剖分。

21.7 Delaunay三角剖分的应用

在经历了实现Delaunay三角剖分所需的繁复细节之后，我们现在可以将其应用于若干重要场景。本节假设你已有一个点的向量（例如vecp），并已调用§21.6中的代码构建了一个Delaunay结构。通常这意味着只需编写一行代码：

Delaunay mygrid(vecp);

那么，下一步该做什么呢？

21.7.1 不规则网格上的二维插值

这可能是前两版《数值 Recipes》中读者最常询问却缺失的算法。其基本设定非常简单：给定平面上的 $N$ 个点，用一种“良好”的三角剖分方法（即偏好短边和大角——换句话说，即Delaunay三角剖分）对这些点进行三角剖分。接着，在每个点上计算你感兴趣的函数值，并将这些值存储在一个向量中（当然，顺序需与点向量一致）。

现在，若要在三角剖分内部（确切地说，是在这些点的凸包内）的一个新点 $\mathbf{p}$ 处插值该函数，就变得很简单了。首先，确定该点落在哪个三角形内。如果你使用Delaunay结构的whichcontainspt()方法，这一步仅需 $O(\log N)$ 次操作。然后，在该三角形三个顶点处的函数值之间进行线性插值。这种线性插值是唯一确定的，因为（想象你的函数在包含 $\mathbf{p}$ 的平面之上的第三维空间中绘出）三个点唯一确定三维空间中的一个平面。

具体而言，可利用重心坐标（如公式(21.3.10)所定义）轻松完成线性插值，而重心坐标又可简化为三次使用三角形面积公式（公式21.3.1）。经适当归一化后，每个重心坐标值恰好对应其相应顶点的权重。

上述思想在以下函数中得以实现：

Doub Delaunay::interpolate(const Point<2> &p, const vector<Doub> &fnvals, Doub defaultval) {
    // 三角网格上的函数插值。
    // 给定任意点p和用于构建Delaunay结构的点处的函数值向量fnvals，
    // 返回p所在三角形内的线性插值函数值。
    // 若p位于三角剖分之外，则返回defaultval。

    Int n, i, j, k;
    Doub wgts[3];
    Int ipts[3];
    Doub sum, ans = 0.0;
    n = whichcontainspt(p);
    if (n < 0) return defaultval;
    for (i = 0; i < 3; i++) ipts[i] = thelist[n].p[i];
    for (i = 0, j = 1, k = 2; i < 3; i++, j++, k++) {
        if (j == 3) j = 0;
        if (k == 3) k = 0;
        wgts[k] = (pts[ipts[j]].x[0] - pts[ipts[i]].x[0]) * (p.x[1] - pts[ipts[i]].x[1])
                  - (pts[ipts[j]].x[1] - pts[ipts[i]].x[1]) * (p.x[0] - pts[ipts[i]].x[0]);
    }
    sum = wgts[0] + wgts[1] + wgts[2];
    if (sum == 0) throw("degenerate triangle");
    for (i = 0; i < 3; i++) ans += wgts[i] * fnvals[ipts[i]] / sum;
    // 线性插值。
    return ans;
}

请注意，你不应期望线性插值具有很高的精度。插值后的函数是分片线性的，在凸包内部连续，但在垂直于三角形边的方向上导数不连续。在三角形边上，它仅在边两端的两个函数值之间进行插值。若要合理表示具有丰富细节结构的函数，你需要大量的三角形。

21.7.2 Voronoi图

大约1907年，乌克兰数学家Georgy Fedoseevich Voronoi重新研究了一个早在1850年就由Dirichlet讨论过的问题：给定平面上的 $N$ 个点（或称“站点”），每个站点 $\mathbf{p}$ 定义了一个区域，该区域中的任意点到 $\mathbf{p}$ 的距离比到其他 $N-1$ 个站点更近。该区域称为 $\mathbf{p}$ 的Voronoi区域。Voronoi区域具有哪些性质？我们又该如何构造它们？

想象一下，城市中的每个人都会去离自己最近的超市购物（“直线距离”），那么Voronoi区域就描绘了每个超市的服务范围。又或者，假设森林中多个地点同时起火，火势以固定速度呈圆形蔓延，那么每个火源烧毁的区域就是其对应的Voronoi区域。

图21.7.1展示了一个Voronoi图的示例，其中40个站点在平面上随机选取。是的，Voronoi区域的边界是多边形，尽管可能是开放的并延伸至无穷远。事实上，站点 $\mathbf{p}$ 的Voronoi区域边界必然由若干线段组成，每条线段都位于 $\mathbf{p}$ 与另一站点 ${\mathbf{q}}_i$ 连线的垂直平分线上。这是因为垂直平分线正是到 $\mathbf{p}$ 和 ${\mathbf{q}}_i$ 距离相等的点的轨迹。因此，真正的问题是：对于给定的 $\mathbf{p}$，哪些 ${\mathbf{q}}_i$ 会贡献边界线段？是否存在一种快速方法来计算这些线段的交点（即Voronoi图的顶点）？

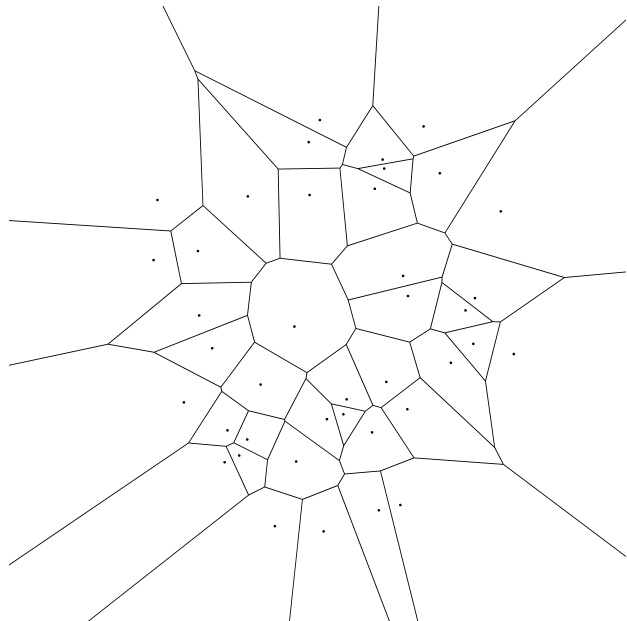
图21.7.1. 40个随机站点的Voronoi图。每个站点都有一个Voronoi区域，即离它比离其他任何站点更近的区域。Voronoi区域的边界是直线段，位于站点对之间的垂直平分线上。

值得注意的是，这些问题完全可以通过对Voronoi站点进行Delaunay三角剖分来解答。（事实上，许多教材以Voronoi图为基本概念，再将Delaunay三角剖分视为其应用。但我们发现反过来更容易理解。）

一些关键事实包括：

• 站点 $\mathbf{p}$ 的Voronoi区域边界上的每条边，都位于一条连接 $\mathbf{p}$ 的Delaunay边的垂直平分线上。
• 实际上，每条Delaunay边恰好对应一条Voronoi边，反之亦然。
• Voronoi图的顶点恰好是Delaunay三角形的外心。
• Voronoi图与Delaunay三角剖分互为对偶图（如果你不了解“对偶图”的含义，也不必担心）。

图21.7.2展示了上述前两个事实证明中的关键思想。我们已经知道边界由若干垂直平分线段构成。我们需要证明：(i) 一个点的所有Delaunay边确实都贡献了一段边界；(ii) 从该点到其他任意站点的连线不会贡献任何边界段。

图(a)展示了站点 $O$ 周围的一小块Delaunay三角剖分。$OA$ 和 $OC$ 的垂直平分线相交于点 $X$，因此 $X$ 是过 $A$、$O$、$C$ 三点的圆的圆心。问题在于Delaunay边 $OB$ 是否会被另外两条边“阻挡”。由于在构造Delaunay三角剖分时，若 $B$ 位于该圆外，则边 $OB$ 将是非法的，因此 $B$ 必须位于该圆内。这意味着 $OB$ 的垂直平分线（标记为 $UV$）必定会“切掉” $X$ 处的角，从而确实为边界贡献了一段线段。

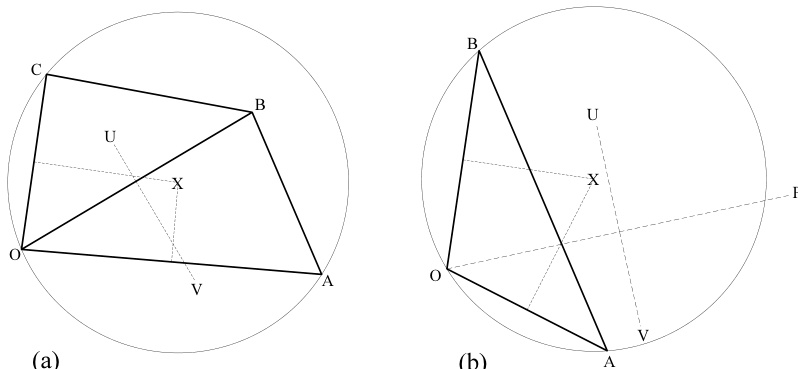
图21.7.2. 证明每条Delaunay边恰好贡献一条位于其垂直平分线上的Voronoi边的关键思想。(a) Delaunay条件要求 $B$ 位于圆 $AOC$ 内，因此其垂直平分线必定在 $X$ 内部切掉一个角。(b) Delaunay条件要求任意其他站点 $P$ 位于圆 $AOB$ 外，因此其垂直平分线无法在 $X$ 内部切掉角。

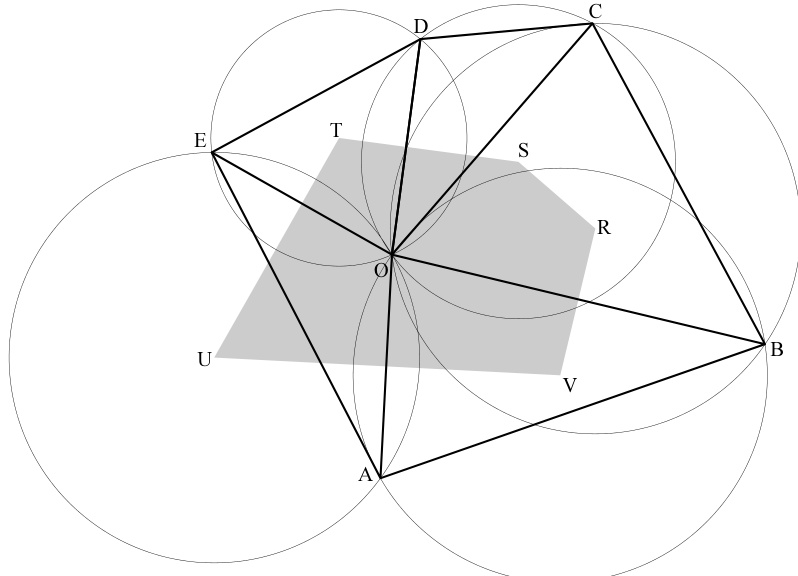
图 21.7.3。围绕点 $O$ 的 Delaunay 三角形的外心构成了 $O$ 的 Voronoi 区域的顶点（图中阴影部分），因为 Delaunay 边的垂直平分线在这些外心处相交。注意，Voronoi 边不一定与其对应的 Delaunay 边实际相交，例如图中的 $SR$ 与 $OC$。

图 (b) 显示了一个 Delaunay 三角形 $OAB$，其边 $OA$ 和 $OB$ 向 $O$ 周围的 Voronoi 边界贡献了垂直平分线段。点 $P$ 是另一个站点。它是否有可能“钻”进来足够近，从而在另外两条平分线之间插入自己的一段平分线？显然不能：我们知道任何 Delaunay 三角形的外接圆内都不包含其他站点。由于 $P$ 必须位于该外接圆之外，其平分线 $UV$ 就无法截断 $X$ 处的角。

Voronoi 顶点即为 Delaunay 三角形的外心，这是前文讨论的直接推论（见图 21.7.3）。外心是各边垂直平分线的交点。由于每条 Delaunay 边都贡献了一段边界，每个这样的外心必然是一个顶点。然而需要注意的是，并非每个 Delaunay 三角形都包含其自身的外心（如图中的 $OCD$），因此 Voronoi 区域边界上的一段边不一定与其对应的 Delaunay 边实际相交（如图中的 $RS$ 与 $OC$）。

我们可以仅通过知道 Voronoi 图的对偶图是 Delaunay 三角剖分，并利用公式 (21.6.1)，来计算具有 $N$ 个站点（其中 $n$ 个位于凸包上）的 Voronoi 图中的边数和顶点数。因此，Voronoi 边的数量即为该公式中的 $L$，而 Voronoi 顶点的数量为 $T$。Voronoi 区域的数量按定义为 $N$。无界的 Voronoi 区域恰好对应于位于站点凸包上的点，因此共有 $n$ 个这样的区域。有趣的是（虽然并非显而易见），每个 Voronoi 区域的平均边数（对所有站点取平均）不超过六。

转向实现代码，定义一个用于存储 Voronoi 边的结构体，以及该边与其所包围站点的关联（通过指向站点列表的整数指针）会很方便。

struct Voredge {
    // Voronoi 图中一条边的结构体，包含其两个端点以及指向其所属站点的整数指针。
    Point<2> p[2];
    Int nearpt;
    Voredge() {}
    Voredge(Point<2> pa, Point<2> pb, Int np) : nearpt(np) {
        p[0] = pa; p[1] = pb;
    }
};

现在可以方便地定义一个 Voronoi 结构体，作为 Delaunay 结构体的派生类。构造函数首先对站点进行 Delaunay 三角剖分，然后遍历所有站点。对于每个站点，首先找到任意一个以该站点为顶点的三角形，然后围绕该站点逆时针循环遍历相邻三角形：通过在 linehash 哈希表中查找相邻三角形的公共边来实现导航。每个三角形的外心即为一个 Voronoi 顶点，在围绕站点遍历时，每两个连续的外心之间存储一条 Voronoi 边。

struct Voronoi : Delaunay {
    // 用于创建 Voronoi 图的结构体，派生自 Delaunay 结构体。
    Int nseg;
    VecInt trindx;
    vector<Voredge> segs;
    Voronoi(vector<Point<2>> pvec);
};

Voronoi::Voronoi(vector<Point<2>> pvec) :
    Delaunay(pvec, 1), nseg(0), trindx(npts), segs(6 * npts + 12) {
    // Voronoi 图的构造函数，输入为站点向量 pvec。
    // 传递位 "1" 给 Delaunay 构造函数，指示其不要删除 linehash。
    Int i, j, k, p, jfirst;
    Ullong key;
    Triel tt;
    Point<2> cc, ccp;
    for (j = 0; j < ntree; j++) {
        if (thelist[j].stat <= 0) continue;
        tt = thelist[j];
        for (k = 0; k < 3; k++) trindx[tt.p[k]] = j;
    }
    for (p = 0; p < npts; p++) {
        // 现在遍历所有站点。
        tt = thelist[trindx[p]];
        if (tt.p[0] == p) { i = tt.p[1]; j = tt.p[2]; }
        else if (tt.p[1] == p) { i = tt.p[2]; j = tt.p[0]; }
        else if (tt.p[2] == p) { i = tt.p[0]; j = tt.p[1]; }
        else throw("triangle should contain p");
        jfirst = j;
        ccp = circumcircle(pts[p], pts[i], pts[j]).center;
        while (i) {
            // 逆时针绕行，寻找外心并存储线段。
            key = hashfn.int64(i) - hashfn.int64(p);
            if (!linehash->get(key, k)) throw("Delaunay is incomplete");
            cc = circumcircle(pts[p], pts[k], pts[i]).center;
            segs[nseg++] = Voredge(ccp, cc, p);
            if (k == jfirst) break; // 绕行完成，正常退出。
            ccp = cc;
            j = i;
            i = k;
        }
    }
}

Voronoi 构造的结果可通过遍历 segs 数组（从 0 到 nseg-1）获得。每个数组元素是一个 Voredge，存储了线段的两个端点以及与其关联的站点编号。注意，每条线段在列表中出现两次，方向相反，因为它依次与两侧的站点相关联。

如果你阅读了上一节中我们关于“小伎俩”的坦白，那么需要记住：那些“开放”的 Voronoi 多边形实际上是通过位于距离站点包围盒尺寸约 bigscale 倍远处的线段闭合的。这些线段包含在 segs 中，但仅出现一次，因为它们的另一侧没有站点。

21.7.3 其他应用

最近邻问题（再探）。连接一个点与其在点集中最近邻的线段，必定是该点集 Delaunay 三角剖分中的一条边。非正式证明：最近邻显然必须对 Voronoi 图的边界有所贡献。正式证明（使用前述定理）：以某点与其最近邻连线为直径的圆内不可能包含其他点（否则那些点会比最近邻更近），因此该直径必为一条 Delaunay 边。

由于我们可以在 $O(N\log N)$ 时间内构造 Delaunay 三角剖分，因此也可以在 $O(N\log N)$ 时间内找出 $N$ 个点的所有最近邻。具体步骤如下：(i) 构造 Delaunay 三角剖分；(ii) 对每个点，绕其一圈（如上文 Voronoi 实现中所示）；(iii) 选取以该点为一端的最短边。

凸包。有时你可能需要知道平面上一组点的凸包以用于其他应用。虽然仅为了获取凸包而构造整个 Delaunay 三角剖分看似浪费，但这种方法其实并不算太差。为了提高效率，在三角剖分过程中可以忽略那些已被发现位于内部三角形中的点。为了将边按逆时针多边形顺序排序，我们在遍历过程中构建一个 nextpt 表记录边的终点，然后一次性遍历该表，按正确顺序输出凸包顶点。

struct Convexhull : Delaunay {
    // 用于构造平面上点集凸包的结构体。
    // 构造完成后，nhull 为凸包中的点数，
    // hullpts[0..nhull-1] 为指向 pvec 中凸包点的整数索引，按逆时针顺序排列。
    Int nhull;
    Int *hullpts;
    Convexhull(vector<Point<2>> pvec);
};

Convexhull::Convexhull(vector<Point<2>> pvec) : Delaunay(pvec, 2), nhull(0) {
    // 凸包构造函数，输入为点向量 pvec。
    // 传递位 "2" 给 Delaunay 构造函数，指示其在可能时忽略内部点以加速。
    Int i, j, k, pstart;
    vector<Int> nextpt(npts);
    for (j = 0; j < ntree; j++) {
        if (thelist[j].stat != -1) continue; // 仅处理凸包边。
        for (i = 0, k = 1; i < 3; i++, k++) {
            if (k == 3) k = 0;
            if (thelist[j].p[i] < npts && thelist[j].p[k] < npts) break;
        }
        if (i == 3) continue; // 未满足条件的情况。
        ++nhull;
        // 成功！将其另一端点存入查找表，并保存其值以防后续使用。
        nextpt[(pstart = thelist[j].p[k])] = thelist[j].p[i];
    }
    if (nhull == 0) throw("no hull segments found");
    hullpts = new Int[nhull];
    j = 0;
    i = hullpts[j++] = pstart;
    while ((i = nextpt[i]) != pstart) hullpts[j++] = i;
}

最大空圆问题。在平面上一组点的凸包内部（严格内部）的最大空圆，其中心必定位于某个 Voronoi 顶点上。因此，你可以遍历所有 Voronoi 顶点，计算以每个顶点为中心的最大圆半径，并取其中的最大值。更好的方法是遍历所有 Delaunay 三角形，计算每个三角形的外心，并选择外接圆半径最大的那个（因为 Delaunay 外心恰好就是 Voronoi 顶点）。想象你要在（凸的）城市范围内开设一家快餐店，希望尽可能远离其他所有快餐店，这就是你要找的最佳位置。

避障路径。如果你想在平面上移动，同时尽可能远离一组点，那么你的路径将沿着 Voronoi 图的边行进。想象你是一名战斗机飞行员，试图避开敌方雷达。

最小生成树。最小生成树（有时称为欧几里得最小生成树）是连接 $N$ 个点的总长度最短的线段集合（参见图 21.7.4）。可以将其想象为连接所有 $N$ 座城市的最便宜高速公路网。它在拓扑上是一棵树（即无环），因为如果存在环，你可以通过删除环中的一条边来节省建设费用。

一个重要定理是：最小生成树是 Delaunay 边的一个子集。你可能会觉得这用处不大，因为它并未指明具体是哪个子集。幸运的是，存在一种快速算法——Kruskal 算法——可用于构造最小生成树。其基本思想是：将所有 Delaunay 边按长度排序，然后从小到大依次将边加入正在生长的树中。

你的树最初由多个互不连通的组件组成，但当

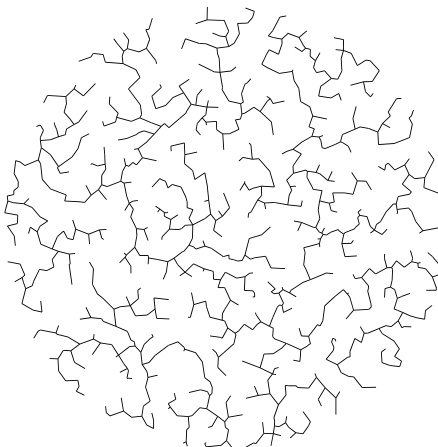
图 21.7.4。圆内 1001 个随机点的最小生成树。该树由 1000 条线段组成，以最短的总长度连接所有点，且是同一组点 Delaunay 三角剖分的一个子集。

当你恰好添加了 $N-1$ 条线段时，整个结构就会连成一个整体，这就是答案。这里只有一个需要注意的地方：在添加线段时，如果某条线段的两个端点已经属于同一个连通分量，则不能添加这条线段（否则会形成环）。因此，你必须为每个顶点维护一个“等价类”关系，使其与所在连通分量中的所有其他顶点等价。我们已经知道如何高效地实现这一点，正如 §8.6 中的 eclass 例程所示。在下面的代码中，采用了类似的逻辑，通过向上追溯指针找到唯一的“母代表”。只要正确实现这一点，该方法的时间复杂度就是 $O(N\log N)$。

Kruskal 算法是一种所谓的贪心算法（greedy algorithm），因为它在每一步都盲目地选择当前最优的边。贪心算法很少能得到真正的全局最优解；但这是一个幸运的情况，它确实能得到最优解。

struct Minspantree : Delaunay {
    // 用于构造平面上点集的最小生成树的结构。
    // 构造完成后，nspan 是线段的数量（始终等于 npts−1），
    // minsega[0..nspan−1] 和 minsegb[0..nspan−1] 包含指向向量 pvec 中点的整数，
    // 表示每条线段的两个端点。
    Int nspan;
    VecInt minsega, minsegb;
    Minspantree(vector<Point<2>> pvec);
};

Minspantree::Minspantree(vector<Point<2>> pvec) :
    Delaunay(pvec, 0), nspan(npts - 1), minsega(nspan), minsegb(nspan) {
    // 构造点向量 pvec 的最小生成树。
    // Delaunay 构造函数给出三角剖分。我们只需从中找出正确的边子集。
    Int i, j, k, jj, kk, m, tmp, nline, n = 0;
    Triel tt;
    nline = ntri + npts - 1;
    VecInt sega(nline);
    VecInt segb(nline);
    VecDoub segd(nline);
    VecInt mo(npts);
    for (j = 0; j < ntri; j++) {
        if (thelist[j].stat == 0) continue;
        tt = thelist[j];
        for (i = 0, k = 1; i < 3; i++, k++) {
            if (k == 3) k = 0;
            if (tt.p[i] > tt.p[k]) continue; // 确保每条边只记录一次。
            if (tt.p[i] >= npts || tt.p[k] >= npts) continue;
            sega[n] = tt.p[i];
            segb[n] = tt.p[k];
            segd[n] = dist(pts[sega[n]], pts[segb[n]]);
            n++;
        }
    }
    Indexx idx(segd);
    for (j = 0; j < npts; j++) mo[j] = j;
    n = -1;
    for (i = 0; i < nspan; i++) {
        for (;;) {
            jj = j = sega[idx[n++]];
            kk = segb[idx[n]];
            while (mo[jj] != jj) jj = mo[jj];
            while (mo[kk] != kk) kk = mo[kk];
            if (jj != kk) {
                minsega[i] = j;
                minsegb[i] = k;
                m = mo[jj] = kk;
                jj = j;
                while (mo[jj] != m) {
                    tmp = mo[jj];
                    mo[jj] = m;
                    jj = tmp;
                }
                kk = k;
                while (mo[kk] != m) {
                    tmp = mo[kk];
                    mo[kk] = m;
                    kk = tmp;
                }
                break;
            }
        }
    }
}

参考文献

de Berg, M., van Kreveld, M., Overmars, M., and Schwarzkopf, O. 2000, Computational Geometry: Algorithms and Applications, 2nd revised ed. (Berlin: Springer), Chapters 7 and 11.

O'Rourke, J. 1998, Computational Geometry in C, 2nd ed. (Cambridge, UK: Cambridge University Press), Chapter 5.

21.8 四叉树与八叉树：存储几何对象

不同于 KD 树的是另一种盒式树结构，通常在二维中称为四叉树（quadtree），在三维中称为八叉树（octree）。是的，我们知道“octree”本应拼作“octtree”，但前者已成为标准用法。我们将四叉树和八叉树统称为“QO 树”，以避免语言上的争议。

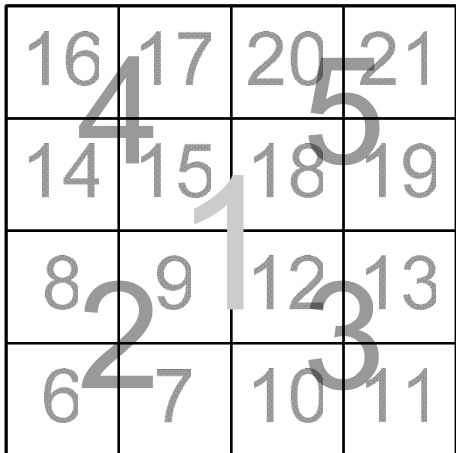
图 21.8.1. 在四叉树中，初始正方形 1 首先被划分为正方形 2、3、4 和 5。在下一层划分中，2 被划分为 6、7、8、9；3 被划分为 10、11、12、13；依此类推。

QO 树从一个有限大小的盒子开始，通常是正方形或立方体，而不是 KD 树所用的近乎无限大的盒子。QO 树在划分每个盒子时，并不像 KD 树那样一次只在一个维度上划分，而是在所有维度上同时划分。因此，一个正方形被划分为四个子正方形，一个立方体被划分为八个子立方体——可谓“子孙满堂”。划分的坐标在每个维度上精确地将母盒子二等分，因此树中同一层的所有盒子都是全等的，与原始盒子相比，尺寸按固定的 2 的幂次缩放。图 21.8.1 展示了二维情况下的这种划分。

因此，QO 树为二维或三维空间提供了一种地址方案。相应地，它们可用于存储和检索能够放入树中某一层盒子的有限大小的几何对象，并用于检测这些对象的相交、邻近关系等。一般思路（尽管可能存在变体）是将每个对象存储在能完全包含它的最小盒子中——或者，对于点这样的零维对象，则存储在我们实现的树的最深层的适当盒子中。然后，在进行碰撞或邻近检测时，我们只遍历树中相关的部分，这与 KD 树的应用类似。

尽管我们仅展示最基本的应用，但 QO 树常常是更复杂算法的核心，例如 [1-3]：

• 视觉平面上的隐藏多边形消除（哪些投影多边形与视场中的给定像素相交？）
• 快速引力或库仑 N 体计算（在不同尺度上存储虚拟对象，以汇总其所包含点质量的多极矩）[4,5,6]
• 网格生成（选择局部网格尺度，以匹配 QO 树中存储障碍物或边界所在的尺度；常使用平衡 QO 树的概念）
• 图像压缩（将图像中缓慢变化的部分作为高层对象存储，并剪除不必要的子节点）。

QO 树的一个主要弱点恰恰源于其几何规则性。如果一个有限大小的对象在存储时恰好落在两个与其尺寸相当的盒子的边界上，

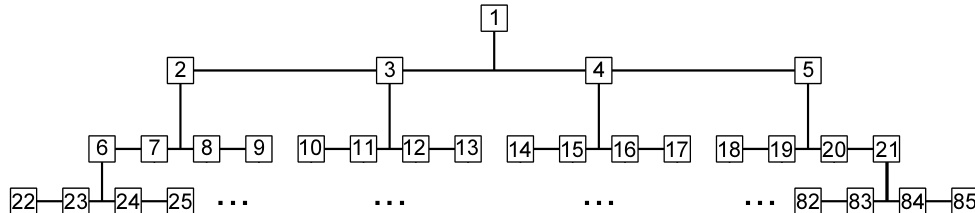
图 21.8.2. 以树形结构展示的四叉树。由于其规则性，四叉树的关系可以用数值描述。例如，盒子 $n$ 的母节点是 $n/4$ 的整数部分。盒子 $n$ 的最左子节点是 $4n-2$。

那么它无法被存储在其中任何一个盒子中。相反，它会被存储在更大的——有时大得多的——盒子中，该盒子首次能完全包含它。如果存储了 $N$ 个“小”对象，那么在二维情况下，落在最高层盒子边界上的对象数量按 $N^{1/2}$ 缩放；在三维情况下，则按 $N^{2/3}$ 缩放。这些对象最终会被存储在树顶层的少数几个盒子中，并参与几乎所有检测碰撞或邻近关系的操作。因此，QO 树通常能将朴素算法的 $N$ 时间复杂度降低到 $N^{1/2}$（二维情况）；但只有在罕见情况或使用专门方法时，才能达到对数 $N$ 或常数时间复杂度的理想境界。尽管如此，一个大数的平方根（或三维情况下的立方根）仍可能是一个巨大的因子，节省的时间非常可观。因此，了解 QO 树是很有价值的。

QO 树的这种几何规则性还允许它们（至少可选地）被实现为一种高效的哈希结构，其中树中的大多数盒子如果为空，则不需要占用存储空间。我们将在此给出这样的实现，既因其固有的优势，也因为使用 §7.6 中的 Hash 和 Mhash 类可以相当简洁地编码。

关键观察来自图 21.8.2，它以树形结构展示了 QO 树。盒子的编号如图 21.8.1 所示，从树根的盒子 1 开始。在这种编号方案下，母盒子与子盒子之间存在简单的数值关系。这使得我们可以在不使用任何存储指针的情况下导航树——向上、向下或横向移动。具体来说，如果 $k\ge 1$ 是一个盒子的编号，则在 $D$ 维（对我们而言是二维或三维）空间中，以下关系成立：

$$\begin{array}{rl}& \text{mother}(k)=\lfloor (k+2^D-2)/2^D\rfloor \\ & \text{leftmost daughter}(k)=2^{D}k-2^D+2\\ & \text{rightmost daughter}(k)=2^{D}k+1\\ & \text{total boxes through level }p=[(2^D{)}^p-1]/(2^D-1)\end{array}$$

注意，由 $[]$ 符号表示的对 $2^D$ 的整数除法可以简单地通过右移 $D$ 位来实现。你应该对照图 21.8.2 验证公式 (21.8.1)，以确保理解其工作原理。树的“层级”从 $p=1$（仅对应盒子 1）开始编号。注意，盒子 1 的母节点计算结果为 0，表示它没有母节点；这在检测祖先循环何时退出时非常方便。

在讨论实现类 Qotree 的细节之前，我们需要先讨论存储在树中的几何对象类所需满足的前提条件。

Qotree 将以类型参数 eLT 作为模板，该参数代表这些对象。要存储一个类型为 eLT 的对象 myel，你必须提供一个方法 myel.isinbox()，其参数是一个 Box，如果 myel 在该盒子内则返回 1，否则返回 0。类似地，要删除一个对象，你需要提供一个 == 运算符，以便通过比较确定要删除的对象。这两个方法就是 Qotree 自身所需的全部。然而，Qotree 的许多应用（包括本节后面展示的一些例子）还需要 myel.contains() 和 myel.collides() 方法中的一个或两个，前者返回 myel 是否包含给定的点，后者返回 myel 是否与另一个类型为 eLT 的元素发生碰撞。

以下是一个简单类的例子，表示圆（当 DIM 为 2 时）或球（当 DIM 为 3 时），它具有这些方法，因此可以与 Qotree 一起存储和处理：

// sphcirc.h
template<Int DIM>
struct Sphcirc {
    // 圆（DIM=2）或球（DIM=3）对象，具有适用于 Qotree 的方法。
    Point<DIM> center;
    Doub radius;
    Sphcirc() {}
    // 默认构造函数用于创建数组。
    Sphcirc(const Point<DIM> &mycenter, Doub myradius)
        : center(mycenter), radius(myradius) {}
    // 通过显式中心和半径构造。
    bool operator==(const Sphcirc &s) const {
        return (radius == s.radius && center == s.center);
    }
    Int isinbox(const Box<DIM> &box) {
        // 圆/球是否在盒子内？
        for (Int i = 0; i < DIM; i++) {
            if ((center.x[i] - radius < box.lo.x[i]) ||
                (center.x[i] + radius > box.hi.x[i])) return 0;
        }
        return 1;
    }
    Int contains(const Point<DIM> &point) {
        // 给定点是否在圆/球内？
        if (dist(point, center) > radius) return 0;
        else return 1;
    }
    Int collides(const Sphcirc<DIM> &circ) {
        // 是否与另一个圆/球碰撞？
        if (dist(circ.center, center) > circ.radius + radius) return 0;
        else return 1;
    }
};

21.8.1 一种基于哈希的QO树实现

我们将使用两个哈希存储结构来实现QO树。第一个是一个Mhash多重映射存储（称为elhash），其键为盒子编号，存储的元素是可能存放在QO树中的几何对象，一个盒子中可能包含多个对象。第二个是一个单值哈希存储（称为pophash），它将一个整数与每个盒子关联起来，这些盒子满足以下任一条件：(i) 包含一个或多个元素（即“已填充”），或 (ii) 是某个已填充盒子的祖先节点。在该整数中，第0位（最低有效位）用于指示该盒子是否已填充，而第 $1\dots 2^D$ 位（即二维情况下为 $1\dots 4$，三维情况下为 $1\dots 8$）用于指示哪些子盒子本身已填充，或是某个已填充盒子的祖先节点。换句话说，pophash结合公式(21.8.1)中定义的关系，替代了传统实现树结构时所需的双向链表指针结构。

我们所能表示的最大层数 $p_{\max }$ 仅受限于用于存储盒子编号 $k$ 的整数类型所能表示的最大值。若使用32位有符号整数，在二维情况下最多可表示16层，因为 $(4^{16}-1)/3<2^{31}-1$（参见公式21.8.1）。在三维情况下，最多可表示11层，因为 $(8^{11}-1)/7<2^{31}-1$。通常并不需要如此高的分辨率（约 $10^9$ 个盒子），因此我们将允许设置一个更小的 $p_{\text{max}}$ 值，这是一个好主意，因为从根节点到叶节点遍历树的一个分支所需的时间（这是其他过程中频繁出现的“原子”操作）与 $p_{\text{max}}$ 成线性关系。

template<class elT, Int DIM> struct Qotree {
    // Quadrree (DIM=2) 或 octree (DIM=3) 对象，用于存储类型为 elT 的几何对象。
    static const Int PMAX = 32/DIM;
    static const Int QO = (1 << DIM);
    static const Int QL = (QO - 2);
    Int maxd;
    Doub blo[DIM];
    Doub bscale[DIM];
    Mhash<Int, elT, Hashfn1> elhash;
    Hash<Int, int, Hashfn1> pophash;
    Qotree(Int hh, Int nv, Int maxdep);
    void setouterbox(Point<DIM> lo, Point<DIM> hi); // 设置尺度和位置。
    Box<DIM> qobox(Int k);
    Int qowhichbox(elT obj);
    Int qostore(elT obj);
    Int qoerase(elT obj);
    Int qoget(Int k, elT *list, Int nmax); // 检索盒子k中的所有对象。
    Int quodump(Int *k, elT *list, Int nmax); // 检索所有对象。
    Int qocollides(elT qt, elT *list, Int nmax);
};

通常在调用qotree构造函数创建QO树后，应立即调用setouterbox()。否则，将使用默认盒子，其一角位于原点，各维度尺寸为1。

首先，我们需要两个辅助例程。第一个例程接收一个盒子编号（例如图21.8.1中的编号），并返回对应的盒子（作为Box<DIM>）。第二个例程接收一个待存储在树中的对象（类型为elT），并返回能包含该对象的最小盒子的编号。它通过从树的顶层开始，尝试每个可能的子盒子，并仅在找到包含关系时才向树的更深层移动。

template<class elT, Int DIM>
Box<DIM> Qotree<elT,DIM>::qobox(Int k) {
    // 返回由k索引的盒子。
    Int j, kb;
    Point<DIM> plo, phi;
    Doub offset[DIM];
    Doub del = 1.0;
    for (j=0; j<DIM; j++) offset[j] = 0.0;
    while (k > 1) {
        kb = (k + QL) % QO;
        for (j=0; j<DIM; j++) { if (kb & (1 << j)) offset[j] += del; }
        k = (k + QL) >> DIM;
        del *= 2.0;
    }
    for (j=0; j<DIM; j++) {
        // 最后，将偏移量按最终的del缩放，
        // 使其度量上正确。
        plo.x[j] = blo[j] + bscale[j]*offset[j]/del;
        phi.x[j] = blo[j] + bscale[j]*(offset[j]+1.0)/del;
    }
    return Box<DIM>(plo,phi);
}

template<class elT, Int DIM>
Int Qotree<elT,DIM>::qowhichbox(elT obj) {
    // 返回能包含元素obj的最小盒子的编号，不考虑obj是否已存储在树中。
    Int p,k,kl,kr,ks=1;
    for (p=2; p<=maxd; p++) {
        kl = QO * ks - QL;
        kr = kl + QO -1;
        for (k=kl; k<=kr; k++) {
            if (obj.isinbox(qobox(k))) { ks = k; break; }
        }
        if (k > kr) break;
    }
    return ks;
}

现在我们可以将元素存入树中，或删除之前存储的元素了。利用上面的qowhichbox()和Mhash的方法，实际的存储或删除操作非常简单。更棘手的是在pophash中创建或删除连接盒子与其祖先的“面包屑”路径。删除时，我们必须确保不会切断通往同一盒子中剩余元素或后代盒子中元素的路径。

template<class elT, Int DIM>
Int Qotree<elT,DIM>::qostore(elT obj) {
    // 将元素obj存储到Qotree中，并返回其存储的盒子编号。
    Int k,ks,kks,km;
    ks = kks = qowhichbox(obj);
    elhash.store(ks, obj);
    pophash[ks] |= 1;
    while (ks > 1) {
        km = (ks + QL) >> DIM;
        k = ks - (QO*km - QL);
        ks = km;
        pophash[ks] |= (1 << (k+1));
    }
    return kks;
}

template<class elT, Int DIM>
Int Qotree<elT,DIM>::qoerase(elT obj) {
    // 删除元素obj，返回其存储的盒子编号；若元素不在Qotree中则返回0。
    // 注意逻辑与qostore非常相似。
    Int k,ks,kks,km;
    Int *ppop;
    ks = kks = qowhichbox(obj);
    if (elhash.erase(ks, obj) == 0) return 0; // 元素不存在！
    if (elhash.count(ks)) return kks; // 同一盒子中仍有其他元素，完成。
    ppop = &pophash[ks];
    *ppop &= ~((Int)1);
    while (ks > 1) {
        if (*ppop) break;
        pophash.erase(ks);
        km = (ks + QL) >> DIM;
        k = ks - (QO*km - QL);
        ks = km;
        ppop = &pophash[ks];
        *ppop &= ~((Int)(1 << (k+1)));
    }
    return kks;
}

最后，我们需要提供方法来检索之前存储的元素，可以是给定编号盒子中的元素，也可以是树中的所有元素。在前一种情况下，Mhash完成所有工作。但在后一种情况下，我们必须提供递归搜索树的机制，因为在任何阶段我们都可能遇到具有多个已填充子盒子的盒子。注意，调用例程负责提供结果的存储空间（作为数组list[]），并声明它准备接受的最大元素数量nmax。

Qotree中声明的附加函数与具体应用相关，我们接下来讨论。

21.8.2 QO树的基本应用

QO树应用的两个重要构建模块是：第一，一个返回所有与指定点相交（即包含该点）的已存储elT元素列表的例程；第二，一个返回所有与指定elT元素相交（即碰撞）的已存储elT元素列表的类似例程。

与一个点相交的元素显然存储在该点所在盒子的祖先盒子中，或与该点在同一盒子中。只需一次从树顶层到底层的遍历即可找到所有此类元素。

template<class elT, Int DIM>
Int Qotree<elT,DIM>::qcontainspt(Point<DIM> pt, elT *list, Int nmax) {
    // 检索Qotree中包含点pt的所有元素（或最多nmax个，若nmax更小）。
    // 元素被复制到list[0..nlist-1]中，并返回nlist (<nmax)。
    Int j,k,ks,pop,nlist;
    Doub bblo[DIM], bbscale[DIM];
    for (j=0; j<DIM; j++) { bblo[j] = blo[j]; bbscale[j] = bscale[j]; }
    nlist = 0;
    ks = 1;
    while (pophash.get(ks,pop)) {
        if (pop & 1) {
            elhash.getinit(ks);
            while (nlist < nmax && elhash.getnext(list[nlist])) {
                if (list[nlist].contains(pt)) nlist++; // 返回包含pt的元素。
            }
        }
        if ((pop >> 1) == 0) break;
        for (k=0, j=0; j<DIM; j++) {
            bbscale[j] *= 0.5;
            if (pt.x[j] > bblo[j] + bbscale[j]) {
                k += (1 << j);
                bblo[j] += bbscale[j];
            }
        }
        if (((pop >> (k+1)) & 1) == 0) break;
        ks = QO * ks - QL + k;
    }
    return nlist;
}

当元素$A$与元素$B$相交时，要么$A$和$B$在同一盒子中，要么$A$在$B$的祖先盒子中，要么$B$在$A$的祖先盒子中。等价地，对于固定的$A$，我们可以通过搜索$A$的盒子、其祖先盒子和其后代盒子来找到所有相交的$B$。后一种搜索需要一个任务列表栈，如我们之前所见（例如在quodump中）。

template<class elT, Int DIM>
Int Qotree<elT,DIM>::qocollides(elT qt, elT *list, Int nmax) {
    // 检索Qotree中与元素qt碰撞的所有元素（或最多nmax个，若nmax更小）。
    // 元素被复制到list[0..nlist-1]中，并返回nlist (≤nmax)。
    Int k,ks,kks,pop,nlist,ntask;
    Int tasklist[200];
    nlist = 0;
    kks = ks = qowhichbox(qt);
    ntask = 0;
    while (ks > 0) {
        // 将起始盒子及其所有祖先放入任务列表。
        tasklist[++ntask] = ks;
        ks = (ks + QL) >> DIM; // 移动到母盒子。
    }
    while (ntask) {
        ks = tasklist[ntask--];
        if (pophash.get(ks,pop) == 0) continue;
        if (pop & 1) {
            elhash.getinit(ks);
            // 盒子已填充，检查其包含的元素。
            while (nlist < nmax && elhash.getnext(list[nlist])) {
                if (list[nlist].collides(qt)) nlist++; // 返回与qt碰撞的元素。
            }
        }
        if (ks >= kks) {
            k = QO*ks - QL;
            while (pop >>= 1) {
                if (pop & 1)
                    tasklist[++ntask] = k;
                k++;
            }
        }
    }
    return nlist;
}

作为QO树的一个简单应用示例，让我们用一个例程复制KDtree::locatenear（§21.2）的功能，该例程查找所有存储点中距离测试点指定半径$r$内的点。使用Sphcirc类，点被表示为半径为零的圆/球，测试点被表示为半径为$r$的圆/球，我们使用qocollides来查找碰撞。

我们将此应用实现为一个结构体Nearpoints，其构造函数从点向量创建QO树，其成员函数locatenear随后可被调用来查找任意指定点周围任意指定半径内的所有存储点。

template <int DIM> struct Nearpoints {
    // 用于构建包含点集的QO树，并重复查询哪些存储点位于指定新点的指定半径内。
    Int npts;
    Qotree<Sphcirc<DIM>,DIM> thetree;
    Sphcirc<DIM> *sphlist;
    Nearpoints(const vector< Point<DIM> > &pvec)
    : npts(pvec.size()), thetree(npts,npts,32/DIM) {
        // 构造函数。从点向量pvec创建QO树。
        Int j,k;
        sphlist = new Sphcirc<DIM>[npts];
        Point<DIM> lo = pvec[0], hi = pvec[0]; // 查找点的包围盒。
        for (j=1; j<npts; j++) for (k=0; k<DIM; k++) {
            if (pvec[j].x[k] < lo.x[k]) lo.x[k] = pvec[j].x[k];
            if (pvec[j].x[k] > hi.x[k]) hi.x[k] = pvec[j].x[k];
        }
        for (k=0; k<DIM; k++) {
            lo.x[k] -= 0.1*(hi.x[k]-lo.x[k]); // 确保点位于内部。
            hi.x[k] += 0.1*(hi.x[k]-lo.x[k]);
        }
        thetree.setouterbox(lo,hi); // 设置树的外包围盒并存储所有点。
        for (j=0; j<npts; j++) thetree.qostore(Sphcirc<DIM>(pvec[j],0.0));
    }
    ~Nearpoints() { delete [] sphlist; }
    Int locatenear(Point<DIM> pt, Doub r, Point<DIM> *list, Int nmax) {
        // 一旦树构建完成，此函数可被重复调用，参数为不同的点pt和半径r。
        // 返回n，即pt周围半径r内的存储点数量（但不超过nmax），
        // 并将这些点复制到list[0..n-1]中。
        Int j,n;
        n = thetree.qocollides(Sphcirc<DIM>(pt,r),sphlist,nmax);
        for (j=0; j<n; j++) list[j] = sphlist[j].center;
        return n;
    }
};

在实践中，对于此应用，上述例程比KDtree::locatenear慢得多，因为在遍历树时涉及大量复制Point和Sphcirc元素以及计算Box的开销。相比之下，KD树非常精简高效，因为它只存储点，并且在我们的实现中，内部将其复制到快速的坐标存储中。

然而，与KD树不同，此处展示的技术可以推广到更复杂的情况。例如，存储的对象可以不是简单的点，而是给定频率下FM广播电台的接收区域，我们可能想知道与拟建新电台发生碰撞的位置。两个广播区域之间的collides()函数可能涉及复杂的计算，考虑它们的功率、周围详细地形等。在这种情况下，当我们试图最小化对collides()的调用次数时，QO树的开销很可能可以忽略不计。

作为另一个简单应用的例子，考虑一个方形的培养皿，孢子随机地、逐个地落在其上。每个这样的孢子会迅速生长成一个圆形菌落，该菌落恰好接触到最近的已有菌落（或培养皿的边缘），然后停止生长。（别问我们为什么，这只是一个例子。）当有 $N$ 个孢子落下后，培养皿会是什么样子？

我们不在此详述代码，仅给出一个简单的描述即可：存储在 QO 树中的对象是圆。对孢子数量进行循环，依次为每个孢子随机选择一个位置。如果 QO 树的方法 qocontainspt() 表明该位置已位于某个已存在的菌落内部，则跳过该孢子，处理下一个。否则，从一个较小的试探半径开始，逐步增大（例如每次加倍），直到 qotreecollides() 首次报告发生碰撞。此时，将试探半径调整为到所有碰撞对象的最小距离，将该菌落加入树中，并继续处理下一个孢子。

图 21.8.3. 孢子随机落在一个方形（！）培养皿上，并生长为刚好接触最近已有菌落或培养皿边缘的菌落。QO 树可用于跟踪碰撞情况。此处已生长出 1000 个达到最大尺寸的菌落。

图 21.8.3 展示了 1000 个菌落生长后的结果配置。（另有 3592 个孢子落在已有菌落内部，立即死亡。）

参考文献

de Berg, M., van Kreveld, M., Overmars, M., and Schwarzkopf, O. 2000, Computational Geometry: Algorithms and Applications, 2nd revised ed. (Berlin: Springer), Chapter 14.[1]

Samet, H. 1990, The Design and Analysis of Spatial Data Structures (Reading, MA: Addison-Wesley).[2]

Samet, H. 1990, Applications of Spatial Data Structures: Computer Graphics, Image Processing, and GIS (Reading, MA: Addison-Wesley).[3]

Pfalzner, S. and Gibbon, P. 1996, Many-Body Tree Methods in Physics (Cambridge, UK: Cambridge University Press).[4]

Greengard, L., and Wandzura, S., eds. 1998, "Fast Multipole Methods," special issue of IEEE Computational Science and Engineering, vol. 5, no. 3 (July–September), pp. 16–56.[5]

Gumerov, N.A., and Duraiswami, R. 2004, Fast Multipole Methods for the Helmholtz Equation in Three Dimensions (Amsterdam: Elsevier).[6]