数值计算相关论文&书籍中文翻译

20.0 引言

偏微分方程（PDE）的数值处理本身就是一个庞大的课题。偏微分方程是许多（如果不是大多数）连续物理系统（如流体、电磁场、人体等）计算机分析或模拟的核心。本章的目的是给出尽可能简明而实用的入门介绍。理想情况下，应该有整整第二卷《数值食谱》专门讨论偏微分方程。（当然，参考文献 [1–4] 提供了现成的替代方案。）

数学家喜欢根据偏微分方程的特征（即信息传播的曲线），将应用中常见的偏微分方程分为三类：双曲型、抛物型和椭圆型。双曲型方程的典型例子是一维波动方程：

$$\frac{{\partial }^{2}u}{\partial t^2}=v^2\frac{{\partial }^{2}u}{\partial x^2}$$

其中 $v=\text{常数}$ 是波的传播速度。抛物型方程的典型例子是扩散方程：

$$\frac{\partial u}{\partial t}=\frac{\partial }{\partial x}\left(D\frac{\partial u}{\partial x}\right)$$

其中 $D$ 是扩散系数。椭圆型方程的典型例子是泊松方程：

$$\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}=\rho (x,y)$$

其中源项 $\rho$ 是给定的。若源项为零，则该方程即为拉普拉斯方程。

从计算的角度来看，将方程划分为这三种典型类型并不是特别有意义——或者至少不如其他一些本质区别重要。方程 (20.0.1) 和 (20.0.2) 都定义了初值问题（或称柯西问题）：如果在某个初始时刻 $t_0$ 对所有 $x$ 给出了关于 $u$ 的信息（可能包括时间导数信息），那么这些方程就描述了 $u(x,t)$ 如何随时间向前传播。换句话说，方程 (20.0.1) 和 (20.0.2) 描述的是

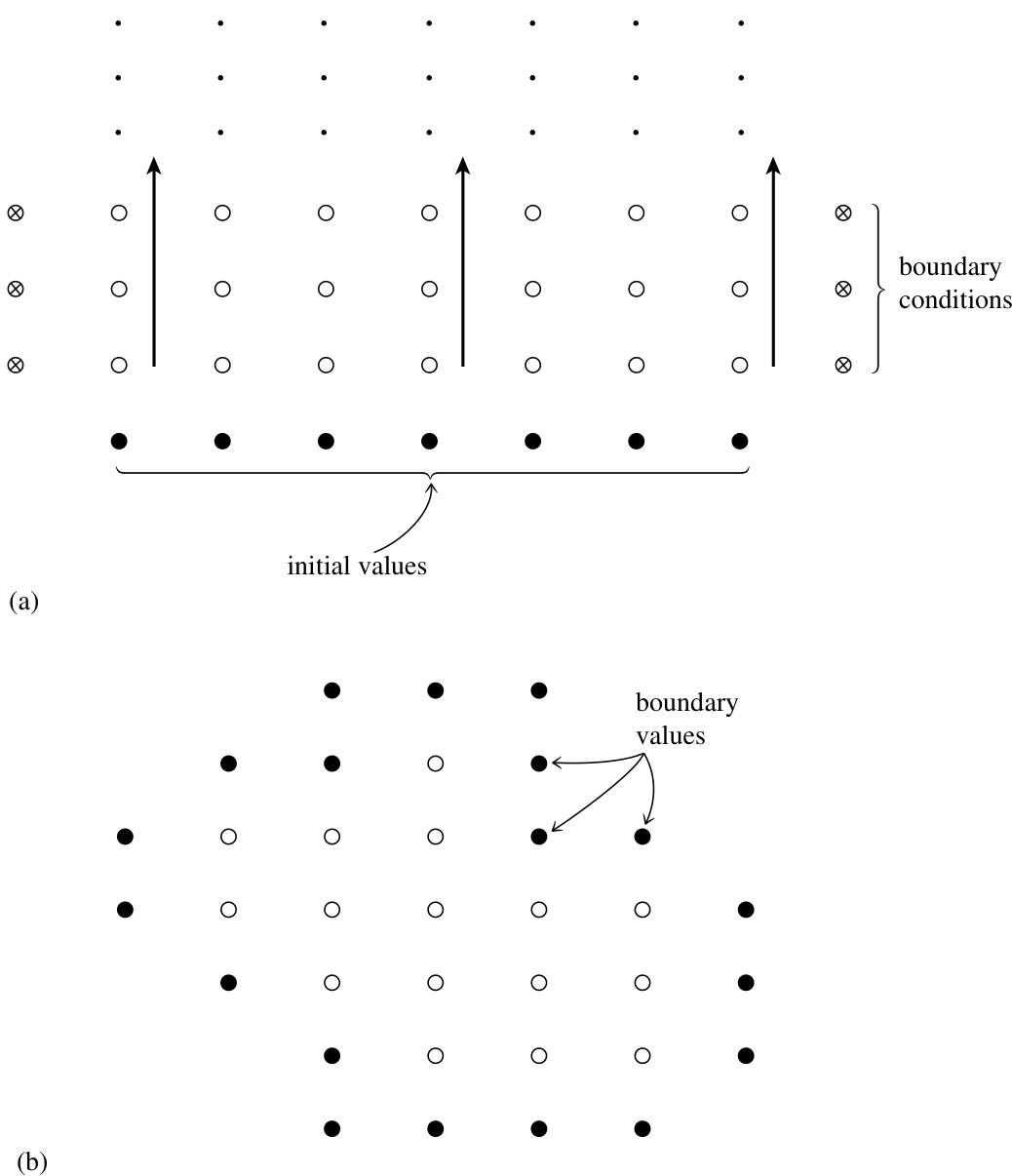
图 20.0.1. 初值问题 (a) 与边值问题 (b) 的对比。在 (a) 中，初始值给定在某一“时间切片”上，目标是沿箭头所示方向推进时间，逐行计算空心点的值。每行左右边界（$\otimes$）处的边界条件也必须提供，但每次只需处理一行。内存中只需保留一行或少数几行即可。在 (b) 中，边界值在网格边缘给定，通过迭代过程求解所有内部点（空心圆）的值。所有网格点都必须保留在内存中。

时间演化。数值程序的目标应是以某种期望的精度追踪这种时间演化。

相比之下，方程 (20.0.3) 要求我们找到一个单一的“静态”函数 $u(x,y)$，使其在感兴趣的 $(x,y)$ 区域内满足该方程，并且——还必须指定——在该区域边界上具有某种期望的行为。这类问题称为边值问题（见图 20.0.1）。一般来说，无法像初值问题那样稳定地“从边界向内积分”。

因此，数值程序的目标是以某种方式一次性在整个区域内收敛到正确的解。

从计算的角度来看，这是最重要的分类：当前的问题是初值问题（时间演化问题）？还是边值问题（静态解问题）？图 20.0.1 强调了这一区别。注意，虽然斜体术语是标准术语，但括号中的术语从计算角度看更能准确描述这种二分法。将初值问题进一步细分为抛物型和双曲型远没有那么重要，原因有二：(i) 许多实际问题属于混合类型；(ii) 正如我们将看到的，当讨论实际计算方案时，大多数双曲型问题都会混入抛物型成分。

20.0.1 初值问题

初值问题由以下问题的答案所定义：

• 哪些是需要随时间向前推进的因变量？

• 每个变量的演化方程是什么？通常这些演化方程都是耦合的，每个方程的右侧会出现多个因变量。

• 每个变量的演化方程中出现的最高阶时间导数是多少？如果可能，应将该时间导数单独放在方程的左侧。为了定义演化过程，不仅需要指定变量的值，还需要指定其所有时间导数（直到最高阶）的值。

• 在感兴趣的空间区域边界上的点，其时间演化受哪些特殊方程（边界条件）支配？例如：狄利克雷条件指定边界点的值作为时间的函数；诺伊曼条件指定边界上的法向梯度值；出射波边界条件正如其名所示。

本章第 20.1–20.3 节讨论了几种不同形式的初值问题。我们并不追求完整性，而是希望通过几个精心挑选的模型示例传达一定量可推广的信息。这些示例将阐明一个重点：算法的稳定性必须是计算中的首要关注点。许多看似合理的初值问题算法实际上并不可行——它们在数值上是不稳定的。

20.0.2 边值问题

边值问题由以下问题所定义：

• 变量是什么？

• 在感兴趣区域的内部满足哪些方程？

• 在感兴趣区域的边界点上满足哪些方程？（对于二阶椭圆型方程，狄利克雷条件和诺伊曼条件是可能的选择，但也可能遇到更复杂的边界条件。）

与初值问题相比，边值问题的稳定性相对容易实现。因此，算法的效率——包括计算量和存储需求——成为主要关注点。

由于边值问题的所有条件必须“同时”满足，这类问题通常（至少在概念上）归结为求解大量联立的代数方程组。当这些方程是非线性的时候，通常通过线性化和迭代方法来求解；因此，在不失一般性的前提下，我们可以将这类问题视为求解特殊的大规模线性方程组。

举个例子——这个例子将在 §20.4–§20.6 中作为我们的“模型问题”反复提及——我们考虑用有限差分法求解方程 (20.0.3)。我们将函数 $u(x,y)$ 用其在如下离散点集上的值来表示：

$$\begin{array}{rl}& x_j=x_0+j\Delta ,j=0,1,\dots ,J\\ & y_l=y_0+l\Delta ,l=0,1,\dots ,L\end{array}$$

其中 $\Delta$ 是网格间距。从现在起，我们将 $u(x_j,y_l)$ 简记为 $u_{j,l}$，$\rho (x_j,y_l)$ 简记为 ${\rho }_{j,l}$。对于方程 (20.0.3)，我们代入一个有限差分格式（见图 20.0.2）：

$$\frac{u_{j+1,l}-2u_{j,l}+u_{j-1,l}}{{\Delta }^2}+\frac{u_{j,l+1}-2u_{j,l}+u_{j,l-1}}{{\Delta }^2}={\rho }_{j,l}$$

或者等价地写成：

$$u_{j+1,l}+u_{j-1,l}+u_{j,l+1}+u_{j,l-1}-4u_{j,l}={\Delta }^2{\rho }_{j,l}$$

为了将这个线性方程组写成矩阵形式，我们需要将 $u$ 排成一个向量。为此，我们将二维网格点按如下方式编号为一维序列：

$$i\equiv j(L+1)+l\text{for}j=0,1,\dots ,J,l=0,1,\dots ,L$$

换句话说，$i$ 沿着代表 $y$ 值的列方向增长最快。于是方程 (20.0.6) 现在变为：

$$u_{i+L+1}+u_{i-(L+1)}+u_{i+1}+u_{i-1}-4u_i={\Delta }^2{\rho }_i$$

该方程仅适用于内部点 $j=1,2,\dots ,J-1$；$l=1,2,\dots ,L-1$。而以下位置的点：

$$\begin{array}{rl}j=0& [i.e.,i=0,\dots ,L]\\ j=J& [i.e.,i=J(L+1),\dots ,J(L+1)+L]\\ l=0& [i.e.,i=0,L+1,\dots ,J(L+1)]\\ l=L& [i.e.,i=L,L+1+L,\dots ,J(L+1)+L]\end{array}$$

是边界点，在这些点上 $u$ 或其导数已被给定。如果我们把所有这些“已知”信息移到方程 (20.0.8) 的右边，则方程就变成如下形式：

$$\mathbf{A}\cdot \mathbf{u}=\mathbf{b}$$

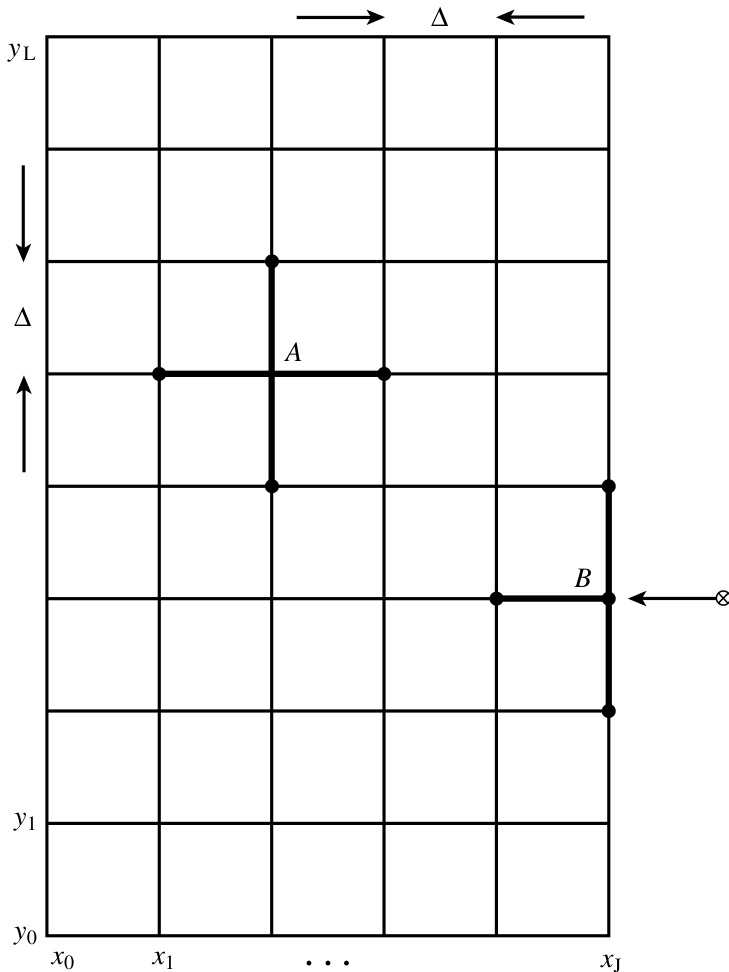
图 20.0.2. 二维网格上二阶椭圆型方程的有限差分表示。点 $A$ 处的二阶导数通过与其相连的点计算；点 $B$ 处的二阶导数则通过相连的点以及示意性表示为 $\otimes$ 的“右侧”边界信息共同计算。

其中矩阵 $\mathbf{A}$ 的结构如图 20.0.3 所示。该矩阵被称为“带边的三对角矩阵”（tridiagonal with fringes）。一般的线性二阶椭圆型方程

$$\begin{array}{r}a(x,y)\frac{{\partial }^{2}u}{\partial x^2}+b(x,y)\frac{\partial u}{\partial x}+c(x,y)\frac{{\partial }^{2}u}{\partial y^2}+d(x,y)\frac{\partial u}{\partial y}\\ +e(x,y)\frac{{\partial }^{2}u}{\partial x\partial y}+f(x,y)u=g(x,y)\end{array}$$

也会导致类似结构的矩阵，只是非零元素不再是常数。

粗略地分类，求解方程 (20.0.10) 有三种不同的方法，并非所有方法都适用于所有情形：松弛法（relaxation methods）、“快速”方法（例如傅里叶方法）以及直接矩阵法。

松弛法直接利用稀疏矩阵 $\mathbf{A}$ 的结构。将该矩阵分解为两部分：

$$\mathbf{A}=\mathbf{E}-\mathbf{F}$$

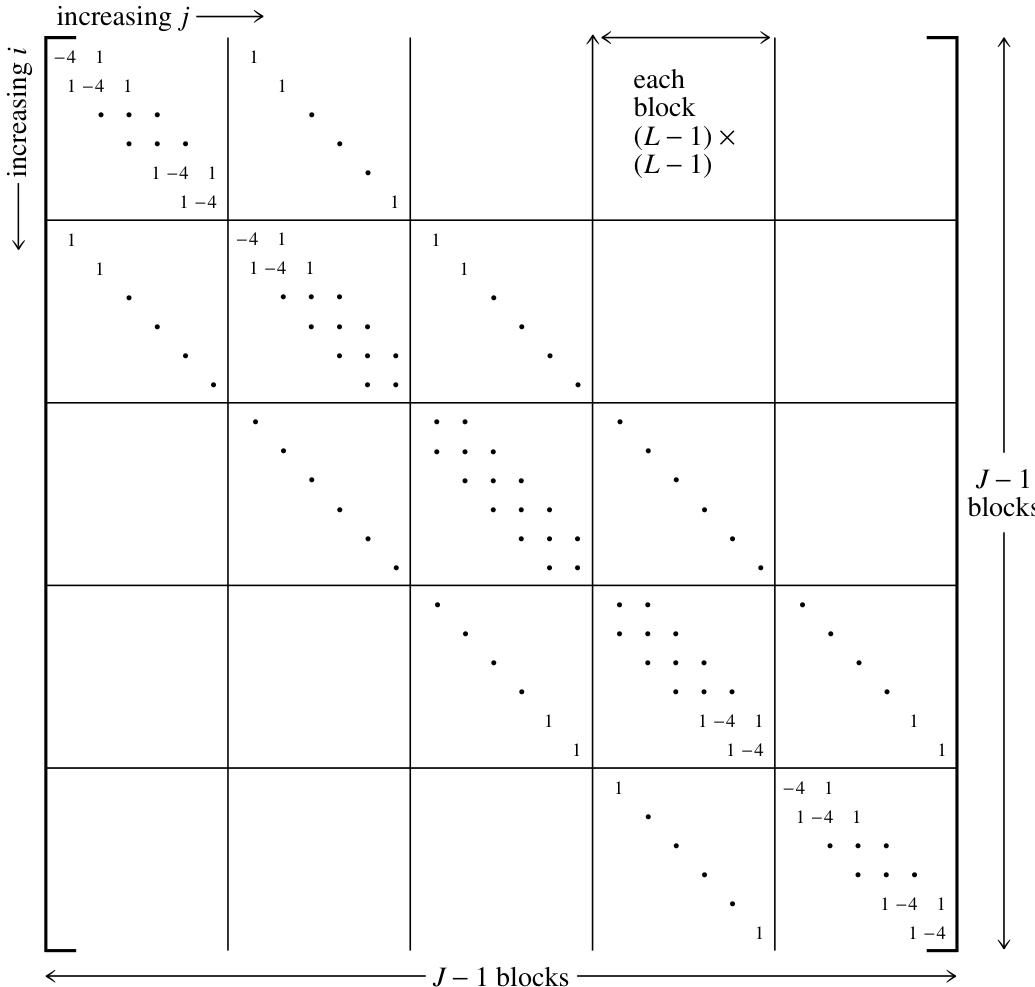
图 20.0.3. 由二阶椭圆型方程（此处为方程 20.0.6）导出的矩阵结构。图中未显示的元素均为零。该矩阵具有三对角的对角块，以及对角线上的子块和超对角块均为对角矩阵。这种形式称为“带边的三对角矩阵”。如此稀疏的矩阵在实际中绝不会以图中所示的完整形式存储。

其中 $\mathbf{E}$ 易于求逆，$\mathbf{F}$ 为剩余部分。于是 (20.0.10) 变为：

$$\mathbf{E}\cdot \mathbf{u}=\mathbf{F}\cdot \mathbf{u}+\mathbf{b}$$

松弛法首先选取一个初始猜测 ${\mathbf{u}}^{(0)}$，然后依次求解迭代序列 ${\mathbf{u}}^{(r)}$：

$$\mathbf{E}\cdot {\mathbf{u}}^{(r)}=\mathbf{F}\cdot {\mathbf{u}}^{(r-1)}+\mathbf{b}$$

由于 $\mathbf{E}$ 被选为易于求逆的形式，因此每次迭代都很快。我们将在 §20.5 和 §20.6 中详细讨论松弛法。

所谓的快速方法 [5] 仅适用于相当特殊的一类方程：即具有常系数的方程，或更一般地，在所选坐标系下可分离变量的方程。此外，边界必须与坐标线重合。这类特殊方程在实际中经常遇到。我们将在 §20.4 中详细讨论。但请注意，§20.6 中讨论的多重网格松弛法（multigrid relaxation methods）可能比“快速”方法更快。

矩阵方法试图直接求解该方程

$$\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$$

直接求解。这种方法的实用性在很大程度上取决于当前问题中矩阵 $\mathbf{A}$ 的具体结构，因此在此我们只能给出一些简要说明和参考文献。

矩阵的稀疏性（sparseness）必须作为指导原则。否则，矩阵问题的规模将变得难以承受。例如，一个在 $1000\times 1000$ 空间网格上的问题将涉及 $10^6$ 个未知量 $u_{j,l}$，这意味着矩阵 $\mathbf{A}$ 的大小为 $10^6\times 10^6$，包含 $10^{12}$ 个元素。若采用非稀疏的 $O(N^3)$ 求解方法，则需要 $O(10^{18})$ 次运算。

正如我们在 §2.7 末尾所讨论的，如果 $\mathbf{A}$ 是对称正定的（这在椭圆型问题中通常是成立的），则可以使用共轭梯度算法。然而在实际应用中，舍入误差常常会削弱共轭梯度算法在求解有限差分方程时的效果。不过，当该算法被整合到某些方法中时仍非常有用——这些方法首先对方程进行改写，使得 $\mathbf{A}$ 被变换为一个接近单位矩阵的矩阵 ${\mathbf{A}}^{\prime }$。此时，由方程定义的二次曲面具有近似球形的等高线，共轭梯度算法便能表现得非常出色。在 §2.7 的例程 linbkg 中，对于非正定问题，我们曾利用类似的预处理技术结合更通用的双共轭梯度法。关于求解偏微分方程中常见的稀疏方程组的迭代方法，已有大量文献资料。入门的好起点包括 [6–8]。

另一类矩阵方法是 §2.7 中描述的“分析—分解—操作”（analyze-factorize-operate）方法。

一般而言，当你有足够的存储空间来实现这些方法时——虽然远不需要上面提到的 $10^{12}$ 量级，但通常仍远多于松弛法所需的存储量——你就应当考虑使用它们。只有多重网格松弛法（§20.6）能与最好的矩阵方法相竞争。然而，对于大于 $1000\times 1000$ 的网格，通常发现只有松弛法（或在适用时的“快速”方法）才是可行的。

20.0.3 生活不止有限差分

除了有限差分法，还有其他求解偏微分方程（PDE）的方法。其中最重要的是有限元法、蒙特卡罗法、谱方法和变分法。遗憾的是，本章几乎只能对有限差分法进行充分讨论，我们将在 §20.7 中对谱方法作简要介绍。本书无法涵盖其他方法。有限元方法 [9–11] 常被固体力学和结构工程领域的从业者所青睐；这些方法允许在需要的位置灵活布置计算单元，这对于处理高度不规则的几何形状尤为重要。

参考文献

Ames, W.F. 1992, Numerical Methods for Partial Differential Equations, 3rd ed. (New York: Academic Press). [1]

Richtmyer, R.D., and Morton, K.W. 1967, Difference Methods for Initial Value Problems, 2nd ed. (New York: Wiley-Interscience); republished 1994 (Melbourne, FL: Krieger). [2]

Roache, P.J. 1998, Computational Fluid Dynamics, revised edition (Albuquerque: Hermosa). [3]

Thomas, J.W. 1995, Numerical Partial Differential Equations: Finite Difference Methods (New York: Springer). [4]

Dorr, F.W. 1970, "The Direct Solution of the Discrete Poisson Equation on a Rectangle," SIAM Review, vol. 12, pp. 248–263. [5]

Saad, Y. 2003, Iterative Methods for Sparse Linear Systems, 2nd ed. (Philadelphia: S.I.A.M.). [6]

Barrett, R., et al. 1993, Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods (Philadelphia: S.I.A.M.). [7]

Greenbaum, A. 1997, Iterative Methods for Solving Linear Systems (Philadelphia: S.I.A.M.). [8]

Reddy, J.N. 2005, An Introduction to the Finite Element Method, 3rd ed. (New York: McGraw-Hill). [9]

Smith, I.M., and Griffiths, V. 2004, Programming the Finite Element Method (New York: Wiley). [10]

Zienkiewicz, O.C., Taylor, R.L., and Zhu, J.Z. 2005, The Finite Element Method: Its Basis and Fundamentals, 6th ed. (Oxford, UK: Elsevier Butterworth-Heinemann). [11]

20.1 通量守恒型初值问题

一大类一维空间中的初值（时间演化）偏微分方程可以写成通量守恒方程的形式：

$$\frac{\partial \mathbf{u}}{\partial t}=-\frac{\partial \mathbf{F}(\mathbf{u})}{\partial x}$$

其中 $\mathbf{u}$ 和 $\mathbf{F}$ 是向量，并且在某些情况下，$\mathbf{F}$ 不仅依赖于 $\mathbf{u}$，还可能依赖于 $\mathbf{u}$ 的空间导数。向量 $\mathbf{F}$ 被称为守恒通量。

例如，典型的双曲型方程——一维波动方程，其传播速度 $v$ 为常数：

$$\frac{{\partial }^{2}u}{\partial t^2}=v^2\frac{{\partial }^{2}u}{\partial x^2}$$

可被重写为如下两个一阶方程组：

$$\begin{array}{r}\frac{\partial r}{\partial t}=v\frac{\partial s}{\partial x}\\ \frac{\partial s}{\partial t}=v\frac{\partial r}{\partial x}\end{array}$$

其中

$$\begin{array}{r}r\equiv v\frac{\partial u}{\partial x}\\ s\equiv \frac{\partial u}{\partial t}\end{array}$$

在这种情况下，$r$ 和 $s$ 成为向量 $\mathbf{u}$ 的两个分量，通量由以下线性矩阵关系给出：

$$\mathbf{F}(\mathbf{u})=\left(\begin{array}{ll}0& -v\\ -v& 0\end{array}\right)\cdot \mathbf{u}$$

（熟悉物理的读者可能会认出方程 (20.1.3) 与描述一维电磁波传播的麦克斯韦方程类似。）

在本节中，我们将考虑通量守恒型方程 (20.1.1) 的一个典型例子，即标量 $u$ 满足的方程：

$$\frac{\partial u}{\partial t}=-v\frac{\partial u}{\partial x}$$

其中 $v$ 为常数。事实上，我们已经知道该方程的通解在解析上是一个沿正 $x$ 方向传播的波：

$$u=f(x-vt)$$

其中 $f$ 是任意函数。然而，我们所发展的数值方法同样适用于更一般的方程 (20.1.1)。在某些情况下，方程 (20.1.6) 被称为对流方程（advective equation），因为量 $u$ 被速度为 $v$ 的“流体流动”所输运。

我们如何对方程 (20.1.6)（或类似地，方程 (20.1.1)）进行有限差分离散化呢？最直接的方法是在 $t$ 轴和 $x$ 轴上均选取等间距的点。因此定义：

$$\begin{array}{rl}& x_j=x_0+j\Delta x,j=0,1,\dots ,J\\ & t_n=t_0+n\Delta t,n=0,1,\dots ,N\end{array}$$

令 $u_j^n$ 表示 $u(t_n,x_j)$。对于时间导数项，我们有多种离散方式。最直观的方式是设：

$${\frac{\partial u}{\partial t}|}_{j,n}=\frac{u_j^{n+1}-u_j^n}{\Delta t}+O(\Delta t)$$

这称为前向欧拉差分（参见方程 (17.1.1)）。虽然前向欧拉方法在 $\Delta t$ 上仅为一阶精度，但其优点在于可以直接利用第 $n$ 步已知的量来计算第 $n+1$ 步的量。对于空间导数，我们可以使用二阶精度的表达式，且仍只使用第 $n$ 步已知的量：

$${\frac{\partial u}{\partial x}|}_{j,n}=\frac{u_{j+1}^n-u_{j-1}^n}{2\Delta x}+O(\Delta x^2)$$

由此得到的方程 (20.1.6) 的有限差分近似称为 FTCS 格式（前向时间、中心空间，Forward Time Centered Space）：

$$\frac{u_j^{n+1}-u_j^n}{\Delta t}=-v\left(\frac{u_{j+1}^n-u_{j-1}^n}{2\Delta x}\right)$$

该式可轻松改写为用其他已知量表示 $u_j^{n+1}$ 的公式。FTCS 格式如图 20.1.1 所示。它是一个推导简单、存储需求小、执行迅速的算法范例。可惜的是，它并不奏效！（见下文。）

FTCS 格式是一种显式格式。这意味着对每个 $j$，$u_j^{n+1}$ 都可以直接由已知量显式计算得出。稍后我们将遇到隐式格式，这类格式要求我们求解耦合不同 $j$ 对应的 $u_j^{n+1}$ 的隐式方程组。（常微分方程的显式与隐式方法已在 §17.5 中讨论过。）FTCS 算法也是单层格式（single-level scheme）的一个例子，因为只需存储第 $n$ 层的值即可计算第 $n+1$ 层的值。

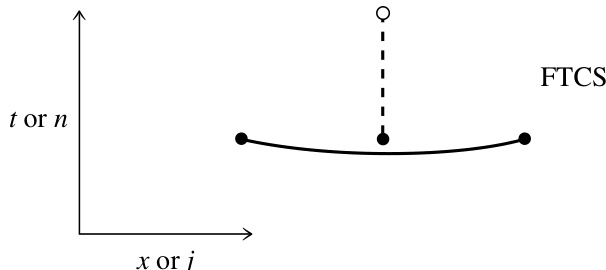
图 20.1. 前向时间中心空间（FTCS）差分格式示意图。在本图及后续图中，空心圆圈表示待求解的新点；实心圆圈表示已知点，其函数值用于计算新点；实线连接用于计算空间导数的点；虚线连接用于计算时间导数的点。FTCS 格式对于双曲型问题通常是不稳定的，一般无法使用。

20.1.1 冯·诺依曼稳定性分析

不幸的是，方程 (20.1.11) 的实用性非常有限。它是一种不稳定的方法，即使能用，也仅适用于研究不到一个振荡周期的极短时间内的波。为了寻找更具普适性的替代方法，我们引入冯·诺依曼稳定性分析（von Neumann stability analysis）。

冯·诺依曼分析是局部的：假设差分方程的系数在空间和时间上变化足够缓慢，以至于可视为常数。在这种情况下，差分方程的独立解（或称本征模）均具有如下形式：

$$u_j^n={\xi }^n{e}^{ikj\Delta x}$$

其中 $k$ 是实的空间波数（可取任意值），$\xi =\xi (k)$ 是依赖于 $k$ 的复数。关键在于，单个本征模的时间演化仅仅是复数 $\xi$ 的整数次幂。因此，若对某些 $k$ 有 $|\xi (k)|>1$，则差分方程是不稳定的（存在指数增长的模）。该复数 $\xi$ 被称为在给定波数 $k$ 下的放大因子（amplification factor）。

为求出 $\xi (k)$，只需将 (20.1.12) 代入 (20.1.11)，并除以 ${\xi }^n$，得到：

$$\xi (k)=1-i\frac{v\Delta t}{\Delta x}\sin (k\Delta x)$$

其模对所有 $k$ 均大于 1；因此 FTCS 格式是无条件不稳定的。

若速度 $v$ 是 $t$ 和 $x$ 的函数，则在方程 (20.1.11) 中应写作 $v_j^n$。但在冯·诺依曼稳定性分析中，我们仍将 $v$ 视为常数，其思想是：当 $v$ 缓慢变化时，该分析在局部成立。事实上，即使在 $v$ 严格为常数的情况下，冯·诺依曼分析也不能严格处理边界点 $j=0$ 和 $j=J$ 处的端点效应。

更一般地，若方程的右端关于 $u$ 是非线性的，则冯·诺依曼分析会通过令 $u=u_0+\delta u$ 并线性化展开来进行处理。

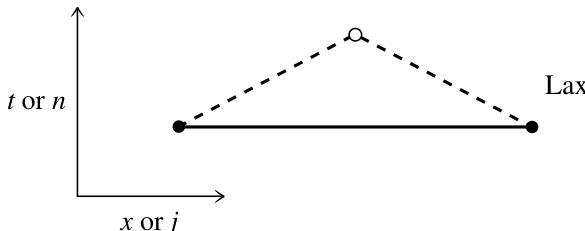
图 20.1.2. 与前图类似，表示 Lax 差分格式。该格式的稳定性判据是 Courant 条件。

在 $\delta u$ 的阶次下进行分析。假设 $u_0$ 量已经精确满足差分方程，则分析将寻找 $\delta u$ 的一个不稳定本征模。

尽管 von Neumann 方法缺乏严格性，但它通常能给出正确的结果，并且比更严谨的方法容易应用得多。因此，我们完全采用该方法。（例如，参见 [1] 中关于其他稳定性分析方法的讨论。）

20.1.2 Lax 方法

FTCS 方法中的不稳定性可以通过 Lax 提出的一个简单修改来消除。将时间导数项中的 $u_i^n$ 替换为其平均值（见图 20.1.2）：

$$u_i^n\to \frac{1}{2}\left(u_{i+1}^n+u_{i-1}^n\right)$$

这将方程 (20.1.11) 变为

$$u_j^{n+1}=\frac{1}{2}\left(u_{j+1}^n+u_{j-1}^n\right)-\frac{v\Delta t}{2\Delta x}\left(u_{j+1}^n-u_{j-1}^n\right)$$

代入方程 (20.1.12)，我们得到放大因子为

$$\xi =\cos k\Delta x-i\frac{v\Delta t}{\Delta x}\sin k\Delta x$$

稳定性条件 $|\xi {|}^2\le 1$ 导致如下要求：

$$\frac{|v|\Delta t}{\Delta x}\le 1$$

这就是著名的 Courant-Friedrichs-Lewy 稳定性判据，通常简称为 Courant 条件。直观上，该稳定性条件可理解如下（见图 20.1.3）：方程 (20.1.15) 中的量 $u_j^{n+1}$ 是由时间 $n$ 时点 $j-1$ 和 $j+1$ 处的信息计算得到的。换句话说，$x_{j-1}$ 和 $x_{j+1}$ 构成了允许向 $u_j^{n+1}$ 传递信息的空间区域的边界。现在回想连续波动方程中，信息实际上以最大速度 $v$ 传播。如果点 $u_j^{n+1}$ 位于图 20.1.3 中阴影区域之外，则它需要来自比差分格式所允许更远点的信息。这种信息的缺失会导致不稳定性。因此，$\Delta t$ 不能取得太大。

图 20.1.3. 差分格式稳定性的 Courant 条件。双曲型问题在某一点的解依赖于过去某个依赖域（图中阴影部分）内的信息。差分格式 (20.1.15) 有其自身的依赖域，由某一时间层上用于确定新点（虚线连接）的若干点（实心点连接）所决定。若差分格式的依赖域大于偏微分方程的依赖域（如 (a) 所示），则该格式满足 Courant 稳定性；若关系相反（如 (b) 所示），则不稳定。对于更复杂的差分格式，其依赖域可能并非仅由最外侧的点决定。

令人惊讶的是，简单的替换 (20.1.14) 竟然能够稳定 FTCS 格式，这是我们首次认识到：对偏微分方程进行差分离散既是一门科学，也是一门艺术。为了稍微揭开这门“艺术”的神秘面纱，让我们通过将方程 (20.1.15) 重写为类似于方程 (20.1.11) 并带有一个余项的形式，来比较 FTCS 与 Lax 格式：

$$\frac{u_j^{n+1}-u_j^n}{\Delta t}=-v\left(\frac{u_{j+1}^n-u_{j-1}^n}{2\Delta x}\right)+\frac{1}{2}\left(\frac{u_{j+1}^n-2u_j^n+u_{j-1}^n}{\Delta t}\right)$$

但这恰好是如下方程的 FTCS 表示：

$$\frac{\partial u}{\partial t}=-v\frac{\partial u}{\partial x}+\frac{(\Delta x{)}^2}{2\Delta t}{\nabla }^{2}u$$

其中在一维情况下 ${\nabla }^2={\partial }^2/\partial x^2$。实际上，我们向方程中添加了一个扩散项，或者如果你还记得粘性流体流动的 Navier-Stokes 方程的形式，也可称之为耗散项。因此，Lax 格式被认为具有数值耗散（或称数值粘性）。我们也可以从放大因子中看出这一点：除非 $|v|\Delta t$ 恰好等于 $\Delta x$，否则 $|\xi |<1$，波的振幅会虚假地衰减。

虚假的衰减难道不和虚假的增长一样糟糕吗？并非如此。我们希望精确研究的尺度是那些跨越许多网格点的尺度，即满足 $k\Delta x\ll 1$。（空间波数 $k$ 由方程 20.1.12 定义。）对于这些尺度，无论在稳定还是不稳定格式中，放大因子都非常接近于 1。因此，稳定格式与不稳定格式在这些尺度上的精度大致相当。然而，对于不稳定格式，我们并不关心的短波尺度（$k\Delta x\sim 1$）会迅速增长并淹没解中有意义的部分。相比之下，采用稳定格式使这些短波无害地衰减要好得多。虽然稳定和不稳定格式在这些短波尺度上都不准确，但在稳定格式下，这种不准确性是可容忍的。

当自变量 $\mathbf{u}$ 为向量时，von Neumann 分析会稍显复杂。例如，我们可以考虑重写后的方程 (20.1.3)：

$$\frac{\partial }{\partial t}\left[\begin{array}{l}r\\ s\end{array}\right]=\frac{\partial }{\partial x}\left[\begin{array}{l}vs\\ vr\end{array}\right]$$

该方程的 Lax 方法为：

$$\begin{array}{r}{r}_j^{n+1}=\frac{1}{2}(r_{j+1}^n+r_{j-1}^n)+\frac{v\Delta t}{2\Delta x}(s_{j+1}^n-s_{j-1}^n)\\ s_j^{n+1}=\frac{1}{2}(s_{j+1}^n+s_{j-1}^n)+\frac{v\Delta t}{2\Delta x}(r_{j+1}^n-r_{j-1}^n)\end{array}$$

此时，von Neumann 稳定性分析假设本征模具有如下（向量）形式：

$$\left[\begin{array}{l}{r}_j^n\\ s_j^n\end{array}\right]={\xi }^n{e}^{ikj\Delta x}\left[\begin{array}{l}{r}^0\\ s^0\end{array}\right]$$

此处右侧的向量是一个（在空间和时间上均）恒定的本征向量，而 $\xi$ 是一个复数，与之前相同。将 (20.1.22) 代入 (20.1.21) 并除以 ${\xi }^n$，得到齐次向量方程：

$$\left[\begin{array}{cc}\cos k\Delta x-\xi & i\frac{v\Delta t}{\Delta x}\sin k\Delta x\\ i\frac{v\Delta t}{\Delta x}\sin k\Delta x& \cos k\Delta x-\xi \end{array}\right]\cdot \left[\begin{array}{l}{r}^0\\ s^0\end{array}\right]=\left[\begin{array}{l}0\\ 0\end{array}\right]$$

该方程有非零解的条件是左侧矩阵的行列式为零，这一条件可轻易推导出两个 $\xi$ 的根：

$$\xi =\cos k\Delta x\pm i\frac{v\Delta t}{\Delta x}\sin k\Delta x$$

稳定性条件是两个根都满足 $|\xi |\le 1$。这再次简化为简单的 Courant 条件（20.1.17）。

20.1.3 其他类型的误差

到目前为止，我们关注的是振幅误差，因为它与差分格式的稳定性或不稳定性密切相关。当我们把关注点从稳定性转向精度时，其他类型的误差就变得相关了。

双曲型方程的有限差分格式可能会表现出色散或相位误差。例如，方程（20.1.16）可以重写为

$$\xi =e^{-ik\Delta x}+i\left(1-\frac{v\Delta t}{\Delta x}\right)\sin k\Delta x$$

任意初始波包是具有不同 $k$ 值的模态的叠加。在每个时间步，这些模态会乘以不同的相位因子（20.1.25），具体取决于它们的 $k$ 值。如果 $\Delta t=\Delta x/v$，那么对于波包 $f(x-vt)$ 的每个模态，若每个模态都乘以 $\exp (-ik\Delta x)$，就能得到精确解。对于这个 $\Delta t$ 值，方程（20.1.25）表明有限差分解给出了精确的解析结果。然而，如果 $v\Delta t/\Delta x$ 不严格等于 1，各模态之间的相位关系可能会严重混乱，导致波包发生色散。从（20.1.25）可以看出，一旦波长与网格间距 $\Delta x$ 相当时，色散效应就会变得显著。

第三种误差与非线性双曲型方程相关，因此有时被称为非线性不稳定性。例如，流体流动的 Euler 方程或 Navier-Stokes 方程中的一部分形式如下：

$$\frac{\partial v}{\partial t}=-v\frac{\partial v}{\partial x}+\dots$$

$v$ 的非线性项会导致傅里叶空间中能量从长波长向短波长转移。这会导致波形逐渐变陡，直至形成垂直剖面或“激波”。由于 von Neumann 分析表明稳定性可能依赖于 $k\Delta x$，因此对平缓波形稳定的格式在陡峭波形下可能变得不稳定。这类问题出现在差分格式中，当傅里叶空间中的级联过程在网格可表示的最短波长（即 $k\sim 1/\Delta x$）处被截断时。如果能量在这些模态中不断累积，最终会淹没我们感兴趣的长波长模态中的能量。

因此，非线性不稳定性和激波形成在一定程度上可以通过数值粘性加以控制，如上文与方程（20.1.18）相关的讨论所述。然而，在某些流体力学问题中，激波形成不仅仅是数值上的麻烦，而是流体实际的物理行为，对其细节的研究正是目标所在。此时，仅靠数值粘性可能不够，或者难以充分控制。这是一个复杂的问题，我们将在下文关于流体动力学的小节中进一步讨论。

对于波动方程，传播误差（振幅或相位）通常最令人担忧。而对于对流方程，输运误差通常更值得关注。在 Lax 格式（方程 20.1.15）中，网格点 $j$ 处被输运量 $u$ 的扰动会在下一个时间步传播到网格点 $j+1$ 和 $j-1$。然而实际上，如果速度 $v$ 为正，则只有网格点 $j+1$ 应受到影响。

改善输运性质的最简单方法是使用迎风差分（见图 20.1.4）：

$$\frac{u_j^{n+1}-u_j^n}{\Delta t}=-v_j^n\{\begin{array}{ll}\frac{u_j^n-u_{j-1}^n}{\Delta x},& v_j^n>0\\ \frac{u_{j+1}^n-u_j^n}{\Delta x},& v_j^n<0\end{array}$$

注意，该格式在空间导数的计算上仅为一阶精度，而非二阶精度。那么它为何能“更好”呢？答案会让数学家感到困扰：数值模拟的目标并不总是严格数学意义上的“精度”，而有时是更宽松、更实用意义上的对底层物理的“保真度”。在这种情况下，某些类型的误差比其他类型更容易被接受。迎风差分通常能提高那些被输运变量可能发生状态突变（例如穿过激波或其他不连续面）的问题的保真度。你必须根据你自己问题的具体特性来做出判断。

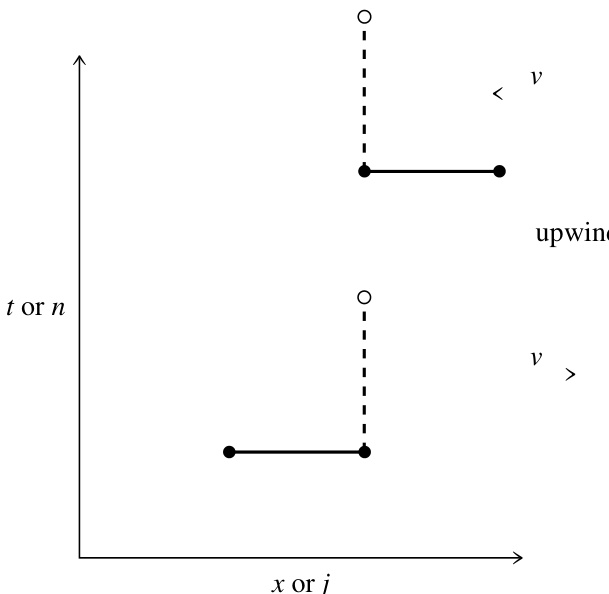
图 20.1.4. 迎风差分格式的示意图。上方格式在对流常数 $v$ 为负时稳定（如图所示）；下方格式在对流常数 $v$ 为正时稳定（亦如图所示）。当然，Courant 条件也必须同时满足。

对于差分格式（20.1.27），其放大因子（对于常数 $v$）为

$$\xi =1-\left|\frac{v\Delta t}{\Delta x}\right|(1-\cos k\Delta x)-i\frac{v\Delta t}{\Delta x}\sin k\Delta x$$

$$|\xi {|}^2=1-2\left|\frac{v\Delta t}{\Delta x}\right|\left(1-\left|\frac{v\Delta t}{\Delta x}\right|\right)(1-\cos k\Delta x)$$

因此，稳定性判据 $|\xi {|}^2\le 1$（再次）简化为 Courant 条件（20.1.17）。

有多种方法可以提高一阶迎风差分的精度。在连续方程中，原本距离为 $v\Delta t$ 的物质经过时间间隔 $\Delta t$ 后到达某一点。而在一阶方法中，物质总是从距离 $\Delta x$ 处到达。如果为了保证精度而要求 $v\Delta t\ll \Delta x$，这可能导致较大的误差。一种减小该误差的方法是在输运前对 $u$ 在 $j-1$ 和 $j$ 之间进行插值。这实际上相当于一种二阶方法。关于二阶迎风差分的各种格式及其比较，见文献 [2,3]。

20.1.4 时间上的二阶精度

当使用时间上一阶精度、空间上二阶精度的方法时，通常必须取 $v\Delta t$ 显著小于 $\Delta x$ 才能达到所需的精度，例如至少小 5 倍。因此，在实践中，Courant 条件实际上并不是这类格式的限制因素。然而，存在一些在时间和空间上均为二阶精度的格式，这些格式通常可以推进到其稳定性极限，从而显著减少计算时间。

例如，守恒方程（20.1.1）的交错蛙跳法（staggered leapfrog method）定义如下（见图 20.1.5）：利用时刻 $t^n$ 的 $u^n$ 值计算通量 $F_i^n$，然后利用通量的时间中心值计算新的 $u^{n+1}$ 值：

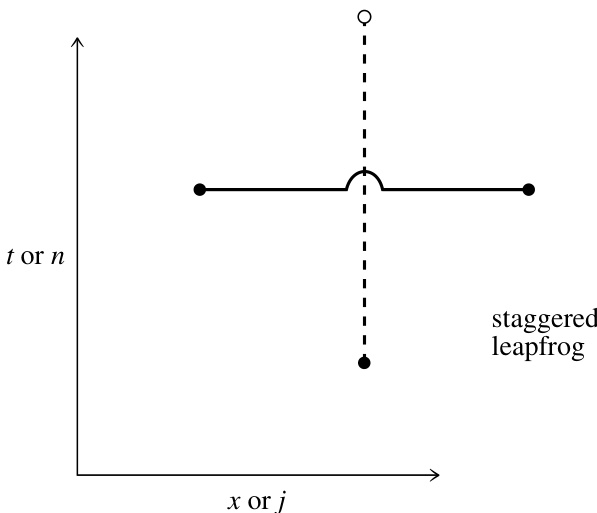
图 20.1.5. 交错蛙跳差分格式的示意图。注意，计算目标点时使用了前两个时间层的信息。该格式在时间和空间上均为二阶精度。

$$u_j^{n+1}-u_j^{n-1}=-\frac{\Delta t}{\Delta x}(F_{j+1}^n-F_{j-1}^n)$$

该方法得名于时间导数项中的时间层“蛙跳”越过空间导数项中的时间层。该方法要求存储 $u^{n-1}$ 和 $u^n$ 以计算 $u^{n+1}$。

对于我们简单的模型方程（20.1.6），交错蛙跳格式的形式为

$$u_j^{n+1}-u_j^{n-1}=-\frac{v\Delta t}{\Delta x}(u_{j+1}^n-u_{j-1}^n)$$

冯·诺依曼稳定性分析现在给出的是关于 $\xi$ 的一个二次方程，而非线性方程，这是因为将特征模态形式 (20.1.12) 代入方程 (20.1.31) 后，出现了 $\xi$ 的三个连续幂次：

$${\xi }^2-1=-2i\xi \frac{v\Delta t}{\Delta x}\sin k\Delta x$$

其解为：

$$\xi =-i\frac{v\Delta t}{\Delta x}\sin k\Delta x\pm \sqrt{1-{\left(\frac{v\Delta t}{\Delta x}\sin k\Delta x\right)}^2}$$

因此，稳定性再次要求满足 Courant 条件。事实上，对于任意满足 $v\Delta t\le \Delta x$ 的情形，方程 (20.1.33) 中均有 $|\xi {|}^2=1$。这正是交错蛙跳法（staggered leapfrog method）的巨大优势：不存在振幅耗散。

对于形如 (20.1.20) 的方程，若将变量置于适当的半网格点上，则交错蛙跳差分格式最为清晰：

$$\begin{array}{r}{r}_{j+1/2}^n\equiv v{\frac{\partial u}{\partial x}|}_{j+1/2}^n=v\frac{u_{j+1}^n-u_j^n}{\Delta x}\\ s_j^{n+1/2}\equiv {\frac{\partial u}{\partial t}|}_j^{n+1/2}=\frac{u_j^{n+1}-u_j^n}{\Delta t}\end{array}$$

这纯粹是一种记号上的便利：我们可以认为 $r$ 和 $s$ 所定义的网格比原始变量 $u$ 所定义的网格精细一倍。方程 (20.1.20) 的蛙跳差分格式为：

$$\begin{array}{r}\frac{r_{j+1/2}^{n+1}-r_{j+1/2}^n}{\Delta t}=\frac{s_{j+1}^{n+1/2}-s_j^{n+1/2}}{\Delta x}\\ \frac{s_j^{n+1/2}-s_j^{n-1/2}}{\Delta t}=v\frac{r_{j+1/2}^n-r_{j-1/2}^n}{\Delta x}\end{array}$$

若将方程 (20.1.22) 代入方程 (20.1.35)，会发现稳定性依然要求满足 Courant 条件，并且当该条件满足时，不存在振幅耗散。

若将方程 (20.1.34) 代入方程 (20.1.35)，可得方程 (20.1.35) 等价于：

$$\frac{u_j^{n+1}-2u_j^n+u_j^{n-1}}{(\Delta t{)}^2}=v^2\frac{u_{j+1}^n-2u_j^n+u_{j-1}^n}{(\Delta x{)}^2}$$

这正是波动方程 (20.1.2) 的“标准”二阶差分格式。可见这是一个两层格式，需要同时利用 $u^n$ 和 $u^{n-1}$ 才能计算出 $u^{n+1}$。在方程 (20.1.35) 中，这一点体现为需要同时使用 $s^{n-1/2}$ 和 $r^n$ 来推进解。

对于比我们简单模型方程更复杂的方程，尤其是非线性方程，当梯度较大时，蛙跳法通常会变得不稳定。这种不稳定性源于奇数和偶数网格点完全解耦，就像国际象棋棋盘上的黑白格子一样，如图 20.1.6 所示。这种网格漂移不稳定性可通过引入数值粘性项来耦合两个网格加以消除，例如在 (20.1.31) 右侧加上一个小系数（$\ll 1$）乘以 $u_{j+1}^n-2u_j^n+u_{j-1}^n$。关于通过添加数值耗散来稳定差分格式的更多内容，参见文献 [4,5]。

两步 Lax-Wendroff 格式是一种时间上二阶精度的方法，可避免较大的数值耗散和网格漂移。该方法在半时间步 $t_{n+1/2}$ 和半网格点 $x_{j+1/2}$ 上定义中间值 $u_{j+1/2}$。这些中间值通过 Lax 格式计算：

$$u_{j+1/2}^{n+1/2}=\frac{1}{2}(u_{j+1}^n+u_j^n)-\frac{\Delta t}{\Delta x}(F_{j+1}^n-F_j^n)$$

利用这些中间变量，可计算通量 $F_{j+1/2}^{n+1/2}$。然后通过适当中心化的表达式计算更新后的值 $u_j^{n+1}$：

$$u_j^{n+1}=u_j^n-\frac{\Delta t}{\Delta x}(F_{j+1/2}^{n+1/2}-F_{j-1/2}^{n+1/2})$$

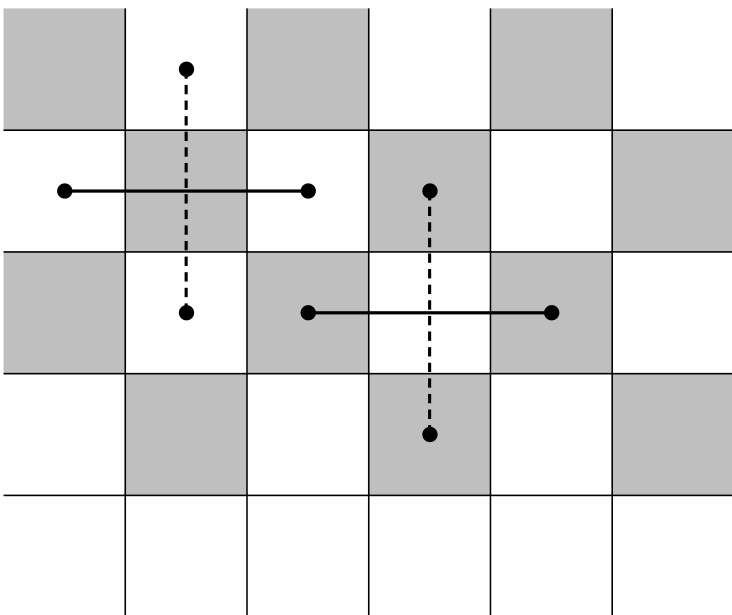
图 20.1.6. 交错蛙跳格式中网格漂移不稳定性的来源。若将网格点想象为位于国际象棋棋盘的格子中，则白格仅与白格耦合，黑格仅与黑格耦合，而黑白格之间无耦合。解决方法是引入一个小的扩散性网格耦合项。

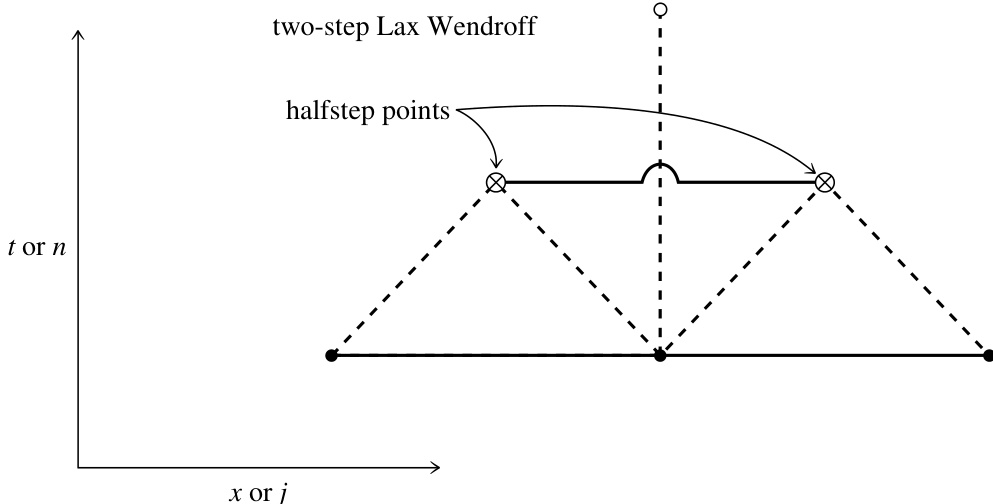
图 20.1.7. 两步 Lax-Wendroff 差分格式的示意图。两个半步点（$\otimes$）通过 Lax 方法计算。这些点加上一个原始点，通过交错蛙跳格式生成新点。半步点仅临时使用，无需在网格上分配存储空间。该格式在空间和时间上均为二阶精度。

中间值 $u_{j+1/2}^{n+1/2}$ 在此之后即被丢弃。（见图 20.1.7。）

现在我们研究该方法对我们模型对流方程（其中 $F=vu$）的稳定性。将 (20.1.37) 代入 (20.1.38)，得到：

$$\begin{array}{r}{u}_j^{n+1}=u_j^n-\alpha [\frac{1}{2}(u_{j+1}^n+u_j^n)-\frac{1}{2}\alpha (u_{j+1}^n-u_j^n)\\ -\frac{1}{2}(u_j^n+u_{j-1}^n)+\frac{1}{2}\alpha (u_j^n-u_{j-1}^n)]\end{array}$$

其中

$$\alpha \equiv \frac{v\Delta t}{\Delta x}$$

于是

$$\xi =1-i\alpha \sin k\Delta x-{\alpha }^2(1-\cos k\Delta x)$$

因此

$$|\xi {|}^2=1-{\alpha }^2(1-{\alpha }^2)(1-\cos k\Delta x{)}^2$$

因此，稳定性判据 $|\xi {|}^2\le 1$ 即为 ${\alpha }^2\le 1$，或通常写作 $v\Delta t\le \Delta x$。顺便提一下，你不应认为 Courant 条件是偏微分方程中唯一会出现的稳定性要求。它在我们的模型例子中反复出现，仅仅是因为这些例子的形式过于简单。然而，所采用的分析方法却是通用的。

除了 $\alpha =1$ 的情况外，(20.1.42) 式中的 $|\xi {|}^2<1$，因此确实会发生一定程度的振幅衰减。然而，对于波长远大于网格尺寸 $\Delta x$ 的情形，这种效应相对较小。若对 (20.1.42) 式在 $k\Delta x$ 较小时进行展开，可得

$$|\xi {|}^2=1-{\alpha }^2(1-{\alpha }^2)\frac{(k\Delta x{)}^4}{4}+\cdots$$

可见，偏离 1 的项仅在 $k$ 的四阶项中出现。这应与 Lax 方法的 (20.1.16) 式进行对比，后者表明对于小的 $k\Delta x$，

$$|\xi {|}^2=1-(1-{\alpha }^2)(k\Delta x{)}^2+\cdots$$

总而言之，对于可表示为通量守恒形式的初值问题，尤其是与波动方程相关的问题，我们建议在可能的情况下使用交错蛙跳法（staggered leapfrog method）。我们个人使用该方法的经验比使用两步 Lax-Wendroff 方法更为成功。对于对输运误差敏感的问题，则应考虑迎风差分法（upwind differencing）或其某种改进形式。

20.1.5 含激波的流体动力学

如前所述，含激波的流体动力学问题的处理已成为一个极其复杂且高度专业化的问题。在此我们所能做的，仅是引导你了解文献中的一些切入点。

目前处理激波主要有三种重要的通用方法。最古老且最简单的方法由 von Neumann 和 Richtmyer 提出，即在方程中加入人工粘性项，以模拟自然界中真实粘性对间断的平滑作用。尝试该方法的一个良好起点是文献 [1] 第 12.11 节中的差分格式。该格式在几乎所有一维空间问题中都表现出色。

第二种方法将适用于光滑流场的高阶差分格式与能有效平滑激波的低阶耗散格式结合起来。通常，各种迎风差分格式通过加权组合，使得在没有陡峭梯度时低阶格式的权重为零，同时满足各种“单调性”约束，以防止数值解中出现非物理振荡。关于这些方法，可从文献 [2,3,6] 入手。

第三种方法，也是潜力最大的方法，是 Godunov 方法。该方法放弃了基于泰勒级数展开的有限差分法中固有的线性化假设，而显式地考虑方程的非线性特性。对于由间断分隔的两个均匀流体状态的演化问题（即 Riemann 激波问题），存在解析解。Godunov 的思想是将流体近似为大量均匀状态的网格单元，并利用 Riemann 解将它们拼接起来。Godunov 方法已被广泛推广，如今统称为高分辨率激波捕捉方法（high resolution shock capturing methods）。其中最具影响力的算法可能是 PPM 方法 [7]。关于高分辨率激波捕捉方法及其他现代算法的综述，可参见文献 [8–10]。

参考文献

Ames, W.F. 1992, Numerical Methods for Partial Differential Equations, 3rd ed. (New York: Academic Press), Chapter 4.

Richtmyer, R.D., and Morton, K.W. 1967, Difference Methods for Initial Value Problems, 2nd ed. (New York: Wiley-Interscience); republished 1994 (Melbourne, FL: Krieger).[1]

Centrella, J., and Wilson, J.R. 1984, "Planar Numerical Cosmology II: The Difference Equations and Numerical Tests," Astrophysical Journal Supplement, vol. 54, pp. 229–249, Appendix B.[2]

Hawley, J.F., Smarr, L.L., and Wilson, J.R. 1984, "A Numerical Study of Black Hole Accretion: II. Finite Differencing and Code Calibration," Astrophysical Journal Supplement, vol. 55, pp. 211–246, §2c.[3]

Kreiss, H.-O., and Busenhart, H. U. 2001, Time-Dependent Partial Differential Equations and Their Numerical Solution (Basel: Birkhäuser), pp. 49.[4]

Gustafsson, B., Kreiss, H.-O., and Oliger, J. 1995, Time Dependent Problems and Difference Methods (New York: Wiley), Ch. 2.[5]

Harten, A., Lax, P.D., and Van Leer, B. 1983, "On Upstream Differencing and Godunov-Type Schemes for Hyperbolic Conservation Laws," SIAM Review, vol. 25, pp. 36–61.[6]

Woodward, P., and Colella, P. 1984, "The Piecewise Parabolic Method (PPM) for Gasdynamical Simulations," Journal of Computational Physics, vol. 54, pp. 174–201; op. cit., vol. 54, pp. 115–173.[7]

LeVeque, R.J. 2002, Finite Volume Methods for Hyperbolic Problems (Cambridge, UK: Cambridge University Press).[8]

LeVeque, R.J. 1992, Numerical Methods for Conservation Laws, 2nd ed. (Basel: Birkhäuser).[9]

Toro, E.F. 1997, Riemann Solvers and Numerical Methods for Fluid Dynamics (Berlin: Springer).[10]

20.2 扩散型初值问题

回顾模型抛物型方程——一维空间中的扩散方程：

$$\frac{\partial u}{\partial t}=\frac{\partial }{\partial x}\left(D\frac{\partial u}{\partial x}\right)$$

其中 $D$ 为扩散系数。实际上，该方程属于上一节讨论的通量守恒形式，其 $x$ 方向的通量为

$$F=-D\frac{\partial u}{\partial x}$$

我们将假设 $D\ge 0$，否则方程 (20.2.1) 将具有物理上不稳定的解：微小扰动会不断集中而非弥散。（切勿试图为本身就不稳定的偏微分方程寻找稳定的差分格式！）

尽管（20.2.1）式已属于我们之前讨论过的形式，但将其视为一个独立的模型仍是有益的。通量（20.2.2）的这种特定形式及其直接推广在实际中经常出现。此外，我们已经看到，在许多其他情况下，数值粘性和人工粘性会引入类似于（20.2.1）式右边的扩散项。

首先考虑 $D$ 为常数的情形。此时方程

$$\frac{\partial u}{\partial t}=D\frac{{\partial }^{2}u}{\partial x^2}$$

可以采用如下显而易见的差分格式：

$$\frac{u_j^{n+1}-u_j^n}{\Delta t}=D\left[\frac{u_{j+1}^n-2u_j^n+u_{j-1}^n}{(\Delta x{)}^2}\right]$$

这仍然是 FTCS 格式，只不过右边差分的是二阶导数。然而，这一点却带来了天壤之别！FTCS 格式对双曲型方程是不稳定的；但稍作计算即可发现，对于方程（20.2.4），其放大因子为

$$\xi =1-\frac{4D\Delta t}{(\Delta x{)}^2}{\sin }^2\left(\frac{k\Delta x}{2}\right)$$

要求 $|\xi |\le 1$，可得稳定性条件：

$$\frac{2D\Delta t}{(\Delta x{)}^2}\le 1$$

物理上，限制条件（20.2.6）意味着：允许的最大时间步长（相差一个数值因子）即为跨越宽度为 $\Delta x$ 的网格单元所需的扩散时间。

更一般地，跨越空间尺度 $\lambda$ 的扩散时间 $\tau$ 的量级为

$$\tau \sim \frac{{\lambda }^2}{D}$$

通常，我们希望精确模拟空间尺度 $\lambda \gg \Delta x$ 的结构的演化。但如果时间步长受限于（20.2.6），那么在感兴趣的尺度上发生显著变化之前，我们需要进行大约 ${\lambda }^2/(\Delta x{)}^2$ 步的计算。这个步数通常是难以接受的。因此，我们必须找到一种稳定的方法，使得时间步长可以与（20.2.7）式给出的时间尺度相当，或者——为了保证精度——略小一些。

这一目标立即引出了一个“哲学性”的问题。显然，我们打算采用的大时间步长对于那些我们不关心的小尺度结构而言将是极其不准确的。我们希望这些小尺度结构表现出某种稳定、无害（“innocuous”），且在物理上不至于太不合理的行为。

我们希望将这种无害的行为内建到我们的差分格式中。那么，这种行为应该是什么样的呢？

对此有两种不同的答案，各有优缺点。第一种答案是寻求一种差分格式，使得小尺度结构迅速趋于其平衡态形式，例如满足将（20.2.3）式左边设为零后的方程。这种答案通常在物理上最为合理；但正如我们将看到的，它导致的差分格式（“全隐式”）对于我们关心的尺度而言，仅具有一阶时间精度。第二种答案则是让小尺度结构保持其初始振幅不变，使得我们关心的大尺度结构的演化叠加在一个“冻结”（尽管仍有涨落）的小尺度背景之上。这种答案给出的差分格式（Crank-Nicolson）具有二阶时间精度。然而，在演化计算接近尾声时，或许希望切换为前一种格式的若干步，以使小尺度结构趋于平衡。现在，让我们看看这些不同的差分格式是如何导出的。

考虑对（20.2.3）式作如下差分：

$$\frac{u_j^{n+1}-u_j^n}{\Delta t}=D\left[\frac{u_{j+1}^{n+1}-2u_j^{n+1}+u_{j-1}^{n+1}}{(\Delta x{)}^2}\right]$$

这与 FTCS 格式（20.2.4）完全类似，只是右边的空间导数在时间层 $n+1$ 上计算。这类格式被称为全隐式（或向后差分），以区别于 FTCS（后者称为全显式）。为求解方程（20.2.8），每一步都需要同时求解关于 $u_j^{n+1}$ 的一组线性方程组。幸运的是，这是一个简单的问题，因为该方程组是三对角的：只需将（20.2.8）式中的项适当整理即可：

$$-\alpha u_{j-1}^{n+1}+(1+2\alpha )u_j^{n+1}-\alpha u_{j+1}^{n+1}=u_j^n,j=1,2,\dots ,J-1$$

其中

$$\alpha \equiv \frac{D\Delta t}{(\Delta x{)}^2}$$

在 $j=0$ 和 $j=J$ 处补充 Dirichlet 或 Neumann 边界条件后，方程（20.2.9）显然构成一个三对角方程组，可利用 §2.4 中的方法在每个时间步轻松求解。

那么，当时间步长非常大时，（20.2.8）式的行为如何？从（20.2.9）式在 $\alpha \to \infty$（即 $\Delta t\to \infty$）的极限下可以最清楚地看出答案。将方程两边除以 $\alpha$，可见差分方程正好对应于平衡方程的有限差分形式：

$$\frac{{\partial }^{2}u}{\partial x^2}=0$$

那么稳定性如何？方程（20.2.8）的放大因子为

$$\xi =\frac{1}{1+4\alpha {\sin }^2\left(\frac{k\Delta x}{2}\right)}$$

显然，对于任意时间步长 $\Delta t$，均有 $|\xi |<1$。因此，该格式是无条件稳定的。对于大 $\Delta t$，从初始条件出发的小尺度演化细节显然是不准确的，

但正如所预期的那样，它确实能得到正确的平衡解。这正是隐式方法的典型特征。

另一方面，下面介绍如何得到我们前述第二种“哲学性”答案，即结合隐式方法的稳定性与同时具有二阶空间和时间精度的方法的准确性。只需将显式和隐式的 FTCS 格式取平均即可：

$$\frac{u_j^{n+1}-u_j^n}{\Delta t}=\frac{D}{2}\left[\frac{(u_{j+1}^{n+1}-2u_j^{n+1}+u_{j-1}^{n+1})+(u_{j+1}^n-2u_j^n+u_{j-1}^n)}{(\Delta x{)}^2}\right]$$

此处等式左右两边均以时间步 $n+\frac{1}{2}$ 为中心，因此该方法在时间上具有二阶精度，正如所声称的那样。其放大因子为

$$\xi =\frac{1-2\alpha {\sin }^2\left(\frac{k\Delta x}{2}\right)}{1+2\alpha {\sin }^2\left(\frac{k\Delta x}{2}\right)}$$

因此该方法对于任意大小的 $\Delta t$ 都是稳定的。此格式称为 Crank-Nicolson 格式，是我们推荐用于任何简单扩散问题的方法（或许可在最后辅以若干完全隐式步）。（参见图 20.2.1。）

现在考虑对简单扩散方程（20.2.3）的一些推广。首先假设扩散系数 $D$ 不是常数，例如 $D=D(x)$。我们可以采用以下两种策略之一。第一种策略是进行解析变量替换：

$$y=\int \frac{dx}{D(x)}$$

于是

$$\frac{\partial u}{\partial t}=\frac{\partial }{\partial x}D(x)\frac{\partial u}{\partial x}$$

变为

$$\frac{\partial u}{\partial t}=\frac{1}{D(y)}\frac{{\partial }^{2}u}{\partial y^2}$$

我们在适当的 ${\gamma }_j$ 处计算 $D$。启发式地，显式格式中的稳定性判据（20.2.6）变为

$$\Delta t\le \underset{j}{\min }\left[\frac{(\Delta y{)}^2}{2D_j^{-1}}\right]$$

注意，在 $y$ 中采用等间距 $\Delta y$ 并不意味着在 $x$ 中也是等间距的。

另一种不需要 $D$ 具有解析可处理形式的方法是直接对原方程（20.2.16）进行差分，并适当地居中处理各项。因此，FTCS 方法变为

$$\frac{u_j^{n+1}-u_j^n}{\Delta t}=\frac{D_{j+1/2}(u_{j+1}^n-u_j^n)-D_{j-1/2}(u_j^n-u_{j-1}^n)}{(\Delta x{)}^2}$$

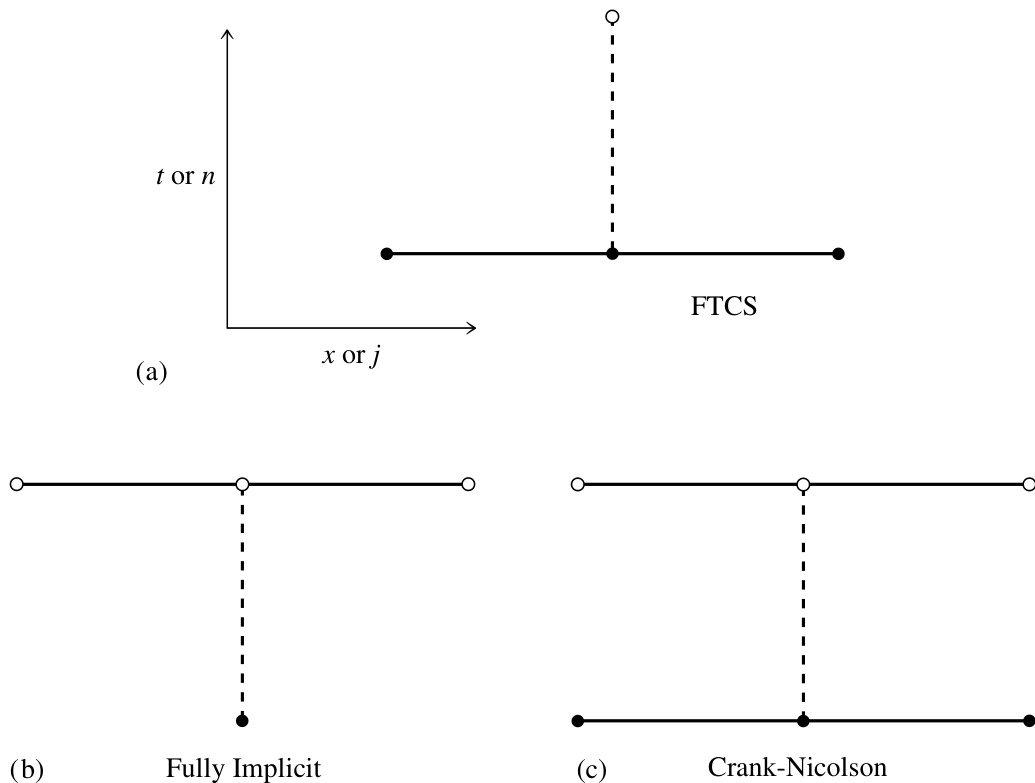
图 20.2.1. 扩散问题的三种差分格式（如图 20.1.2 所示）。（a）前向时间中心空间格式具有一阶精度，但仅在时间步足够小时才稳定。（b）全隐式格式对任意大的时间步都稳定，但仍只具有一阶精度。（c）Crank-Nicolson 格式具有二阶精度，且通常对大时间步也是稳定的。

其中

$$D_{j+1/2}\equiv D(x_{j+1/2})$$

其启发式稳定性判据为

$$\Delta t\le \underset{j}{\min }\left[\frac{(\Delta x{)}^2}{2D_{j+1/2}}\right]$$

Crank-Nicolson 方法也可以类似地推广。

第二种需要考虑的复杂情况是非线性扩散问题，例如 $D=D(u)$。显式格式可以以显而易见的方式推广。例如，在方程（20.2.19）中令

$$D_{j+1/2}=\frac{1}{2}\left[D(u_{j+1}^n)+D(u_j^n)\right]$$

隐式格式则不那么容易处理。若将（20.2.22）中的 $n$ 替换为 $n+1$，则每一步时间步都需要求解一组复杂的耦合非线性方程。通常存在更简便的方法：如果 $D(u)$ 的形式允许我们解析地积分

$$dz=D(u)du$$

得到 $z(u)$，则（20.2.1）的右端变为 ${\partial }^{2}z/\partial x^2$，我们可以将其隐式差分为

$$\frac{z_{j+1}^{n+1}-2z_j^{n+1}+z_{j-1}^{n+1}}{(\Delta x{)}^2}$$

现在对方程（20.2.24）右边的每一项进行线性化，例如

$$\begin{array}{r}{z}_j^{n+1}\equiv z(u_j^{n+1})=z(u_j^n)+(u_j^{n+1}-u_j^n){\frac{\partial z}{\partial u}|}_{j,n}\\ =z(u_j^n)+(u_j^{n+1}-u_j^n)D(u_j^n)\end{array}$$

这再次将问题简化为三对角形式，并且在实践中通常保留全隐式差分法的稳定性优势。

20.2.1 薛定谔方程

有时所求解的物理问题会对差分格式施加一些我们尚未考虑的约束条件。例如，考虑量子力学中的含时薛定谔方程。该方程本质上是一个关于复数量 $\psi$ 演化的抛物型方程。对于一维势场 $V(x)$ 对波包的散射问题，该方程具有如下形式：

$$i\frac{\partial \psi }{\partial t}=-\frac{{\partial }^2\psi }{\partial x^2}+V(x)\psi$$

（此处我们选取了单位制，使得普朗克常数 $\hslash =1$，粒子质量 $m=1/2$。）给定初始波包 $\psi (x,t=0)$ 以及边界条件 $\psi \to 0$（当 $x\to \pm \infty$ 时）。假设我们满足于时间上的一阶精度，但出于稳定性考虑希望采用隐式格式。对式 (20.2.8) 稍作推广，可得：

$$i\left[\frac{{\psi }_j^{n+1}-{\psi }_j^n}{\Delta t}\right]=-\left[\frac{{\psi }_{j+1}^{n+1}-2{\psi }_j^{n+1}+{\psi }_{j-1}^{n+1}}{(\Delta x{)}^2}\right]+V_j{\psi }_j^{n+1}$$

其对应的放大因子为：

$$\xi =\frac{1}{1+i\left[\frac{4\Delta t}{(\Delta x{)}^2}{\sin }^2\left(\frac{k\Delta x}{2}\right)+V_j\Delta t\right]}$$

该格式是无条件稳定的，但不幸的是它不是幺正的。而底层物理问题要求粒子在空间某处被找到的总概率始终保持为 1。这在数学上体现为 $\psi$ 的模平方范数保持为 1：

$${\int }_{-\infty }^{\infty }|\psi {|}^{2}dx=1$$

初始波函数 $\psi (x,0)$ 被归一化以满足式 (20.2.29)。薛定谔方程 (20.2.26) 则保证了该条件在所有后续时刻均成立。

我们将方程 (20.2.26) 写成如下形式：

$$i\frac{\partial \psi }{\partial t}=H\psi$$

其中算符 $H$ 为：

$$H=-\frac{{\partial }^2}{\partial x^2}+V(x)$$

方程 (20.2.30) 的形式解为：

$$\psi (x,t)=e^{-iHt}\psi (x,0)$$

其中算符的指数函数由其幂级数展开定义。

不稳定的显式 FTCS 格式将式 (20.2.32) 近似为：

$${\psi }_i^{n+1}=(1-iH\Delta t){\psi }_i^n$$

其中 $H$ 用关于 $x$ 的中心差分近似表示。相比之下，稳定的隐式格式 (20.2.27) 为：

$${\psi }_i^{n+1}=(1+iH\Delta t{)}^{-1}{\psi }_i^n$$

这两种格式在时间上都是一阶精度的，这一点可通过展开式 (20.2.32) 看出。然而，式 (20.2.33) 和 (20.2.34) 中的算符均非幺正。

正确离散薛定谔方程的方法 [1,2] 是采用 Cayley 形式来表示 $e^{-iHt}$ 的有限差分近似，该方法具有二阶精度且保持幺正性：

$$e^{-iHt}\simeq \frac{1-\frac{1}{2}iH\Delta t}{1+\frac{1}{2}iH\Delta t}$$

换句话说，

$$(1+\frac{1}{2}iH\Delta t){\psi }_i^{n+1}=(1-\frac{1}{2}iH\Delta t){\psi }_i^n$$

将 $H$ 用其关于 $x$ 的有限差分近似代替后，我们得到一个复系数的三对角方程组需要求解。该方法是稳定的、幺正的，并且在空间和时间上均为二阶精度。事实上，这正是再次应用了 Crank-Nicolson 方法！

参考文献

Thomas, J.W. 1995, Numerical Partial Differential Equations: Finite Difference Methods (New York: Springer).

Ames, W.F. 1992, Numerical Methods for Partial Differential Equations, 3rd ed. (New York: Academic Press), 第2章。

Goldberg, A., Schey, H.M., and Schwartz, J.L. 1967, “Computer-Generated Motion Pictures of One-Dimensional Quantum-Mechanical Transmission and Reflection Phenomena,” American Journal of Physics, vol. 35, pp. 177–186.[1]

Galbraith, I., Ching, Y.S., and Abraham, E. 1984, “Two-Dimensional Time-Dependent Quantum-Mechanical Scattering Event,” American Journal of Physics, vol. 52, pp. 60–68.[2]

20.3 多维初值问题

§20.1 和 §20.2 中针对 $1+1$ 维问题（一个空间维加一个时间维）所描述的方法可以很容易地推广到 $N+1$ 维。然而，随着维数的增加，求解所得方程所需的计算能力会急剧增长。如果你用 100 个空间网格点求解了一个一维问题，那么求解二维版本的问题（使用 $100\times 100$ 的网格点）至少需要 100 倍的计算量。因此，在多维问题中，你通常不得不满足于非常有限的空间分辨率。

请允许我们给出一点关于多维偏微分方程（PDE）代码开发与测试的建议：你应该始终先在非常小的网格（例如 $8\times 8$）上运行你的程序，即使由此得到的精度差到毫无用处。只有当你的程序完全调试完毕并明显稳定之后，才能将网格尺寸增大到合理的规模，并开始分析结果。我们甚至曾听到有人辩解道：“我的程序在粗糙网格上不稳定，但我确信在更大的网格上这种不稳定性会消失。” 这种说法是极其有害的谬论，完全混淆了精度与稳定性这两个概念。事实上，新的不稳定性有时确实会在更大的网格上出现；但旧的不稳定性（据我们的经验）绝不会自行消失。

由于不得不使用较小的网格尺寸，有些人建议采用更高阶的方法以试图提高精度。这种做法可能非常危险。除非你所求解的问题已知是光滑的，并且你所采用的高阶方法已被证明极其稳定，否则我们不建议时间方向的精度超过二阶（对于一阶方程组而言）。对于空间差分，我们建议采用与原始偏微分方程阶数相同的差分阶数，对于空间上为一阶的偏微分方程，最多允许使用二阶空间差分。当你将差分方法的阶数提高到超过原始偏微分方程的阶数时，就会在差分方程中引入虚假解。如果这些虚假解恰好都呈指数衰减，那倒不会造成问题；否则，你将会看到灾难性的后果！

20.3.1 通量守恒方程的 Lax 方法

作为例子，我们现在展示如何将 Lax 方法（20.1.15）推广到二维情形，用于求解守恒方程

$$\frac{\partial u}{\partial t}=-\nabla \cdot \mathbf{F}=-\left(\frac{\partial F_x}{\partial x}+\frac{\partial F_y}{\partial y}\right)$$

采用如下空间网格：

$$\begin{array}{r}{x}_j=x_0+j\Delta \\ y_l=y_0+l\Delta \end{array}$$

为简便起见，我们取 $\Delta x=\Delta y\equiv \Delta$。于是 Lax 格式为

$$\begin{array}{r}{u}_{j,l}^{n+1}=\frac{1}{4}(u_{j+1,l}^n+u_{j-1,l}^n+u_{j,l+1}^n+u_{j,l-1}^n)\\ -\frac{\Delta t}{2\Delta }(F_{j+1,l}^n-F_{j-1,l}^n+F_{j,l+1}^n-F_{j,l-1}^n)\end{array}$$

注意，这里简写符号 $F_{j+1}$ 和 $F_{j-1}$ 指的是 $F_x$，而 $F_{l+1}$ 和 $F_{l-1}$ 指的是 $F_y$。

现在我们对模型对流方程（即 (20.1.6) 的二维类比）进行稳定性分析，其中

$$F_x=v_{x}u,F_y=v_{y}u$$

这需要一个在空间上具有二维形式的本征模，但在时间上仍仅具有对 $\xi$ 的简单幂次依赖关系：

$$u_{j,l}^n={\xi }^n{e}^{i{k}_{x}j\Delta }{e}^{i{k}_{y}l\Delta }$$

将其代入方程 (20.3.3)，可得

$$\xi =\frac{1}{2}(\cos k_x\Delta +\cos k_y\Delta )-i{\alpha }_x\sin k_x\Delta -i{\alpha }_y\sin k_y\Delta$$

其中

$${\alpha }_x=\frac{v_x\Delta t}{\Delta },{\alpha }_y=\frac{v_y\Delta t}{\Delta }$$

$|\xi {|}^2$ 的表达式可整理为如下形式：

$$\begin{array}{r}|\xi {|}^2=1-({\sin }^2{k}_x\Delta +{\sin }^2{k}_y\Delta )[\frac{1}{2}-({\alpha }_x^2+{\alpha }_y^2)]\\ -\frac{1}{4}(\cos k_x\Delta -\cos k_y\Delta {)}^2-({\alpha }_y\sin k_x\Delta -{\alpha }_x\sin k_y\Delta {)}^2\end{array}$$

最后两项为负，因此稳定性条件 $|\xi {|}^2\le 1$ 转化为

$$\frac{1}{2}-({\alpha }_x^2+{\alpha }_y^2)\ge 0$$

即

$$\Delta t\le \frac{\Delta }{\sqrt{2}(v_x^2+v_y^2{)}^{1/2}}$$

这是 $N$ 维 Courant 条件的一般结果示例：如果 $|v|$ 是问题中的最大传播速度，则

$$\Delta t\le \frac{\Delta }{\sqrt{N}|v|}$$

即为 Courant 条件。

20.3.2 多维扩散方程

考虑二维扩散方程：

$$\frac{\partial u}{\partial t}=D\left(\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}\right)$$

显式方法（例如 FTCS）可以以显而易见的方式从一维情形推广而来。然而，我们已经看到，扩散问题通常最好采用隐式方法处理。假设我们尝试在二维情形下实现 Crank-Nicolson 格式，这将给出：

$$u_{j,l}^{n+1}=u_{j,l}^n+\frac{1}{2}\alpha \left({\delta }_x^2{u}_{j,l}^{n+1}+{\delta }_x^2{u}_{j,l}^n+{\delta }_y^2{u}_{j,l}^{n+1}+{\delta }_y^2{u}_{j,l}^n\right)$$

其中

$$\alpha \equiv \frac{D\Delta t}{{\Lambda }^2}\Delta \equiv \Delta x=\Delta y$$

$${\delta }_x^2{u}_{j,l}^n\equiv u_{j+1,l}^n-2u_{j,l}^n+u_{j-1,l}^n$$

${\delta }_y^2{u}_{j,l}^n$ 的定义类似。这无疑是一个可行的格式；问题在于求解耦合的线性方程组。在一维空间中，该方程组是三对角的，但在二维情形下不再如此，尽管矩阵仍然非常稀疏。一种可能的解决方法是使用适当的稀疏矩阵技术（参见 §2.7 和 §20.0）。

另一种通常更受青睐的可能性是对 Crank-Nicolson 算法进行稍有不同的推广。该方法在时间和空间上仍具有二阶精度，并且无条件稳定，但其方程比 (20.3.13) 更容易求解。这种方法称为交替方向隐式法（ADI），它体现了算子分裂（或称时间分裂）这一强大概念，我们将在下文进一步讨论。其基本思想是将每个时间步长 $\Delta t$ 分为两个子步长 $\Delta t/2$。在每个子步中，对不同维度进行隐式处理：

$$\begin{array}{r}{u}_{j,l}^{n+1/2}=u_{j,l}^n+\frac{1}{2}\alpha \left({\delta }_x^2{u}_{j,l}^{n+1/2}+{\delta }_y^2{u}_{j,l}^n\right)\\ u_{j,l}^{n+1}=u_{j,l}^{n+1/2}+\frac{1}{2}\alpha \left({\delta }_x^2{u}_{j,l}^{n+1/2}+{\delta }_y^2{u}_{j,l}^{n+1}\right)\end{array}$$

该方法的优点在于，每个子步仅需解一个简单的三对角方程组。

20.3.3 一般的算子分裂方法

算子分裂（也称为时间分裂或分数步长法）的基本思想如下：假设你有一个如下形式的初值问题：

$$\frac{\partial u}{\partial t}=\mathcal{L}u$$

其中 $\mathcal{L}$ 是某个算子。虽然 $\mathcal{L}$ 不一定是线性的，但假设它至少可以表示为作用于 $u$ 的 $m$ 个部分的线性叠加：

$$\mathcal{L}u={\mathcal{L}}_{1}u+{\mathcal{L}}_{2}u+\cdots +{\mathcal{L}}_{m}u$$

最后，假设对于每个部分，你已经知道一种差分格式，可以在该部分算子单独作为右端项时，将变量 $u$ 从时间步 $n$ 更新到 $n+1$。我们将这些更新操作符号化地写作：

$$\begin{array}{r}{u}^{n+1}={\mathcal{U}}_1(u^n,\Delta t)\\ u^{n+1}={\mathcal{U}}_2(u^n,\Delta t)\\ \dots \end{array}$$

$$u^{n+1}={\mathcal{U}}_m(u^n,\Delta t)$$

现在，一种形式的算子分裂方法是通过以下一系列更新操作从 $n$ 推进到 $n+1$：

$$\begin{array}{r}{u}^{n+(1/m)}={\mathcal{U}}_1(u^n,\Delta t)\\ u^{n+(2/m)}={\mathcal{U}}_2(u^{n+(1/m)},\Delta t)\end{array}$$

$$u^{n+1}={\mathcal{U}}_m(u^{n+(m-1)/m},\Delta t)$$

例如，对于如下形式的对流-扩散方程：

$$\frac{\partial u}{\partial t}=-v\frac{\partial u}{\partial x}+D\frac{{\partial }^{2}u}{\partial x^2}$$

可以对对流项采用显式格式，而对扩散项采用 Crank-Nicolson 或其他隐式格式，从而获得更好的效果。

交替方向隐式（ADI）方法，即方程（20.3.16），是算子分裂的一个例子，但略有不同。让我们重新解释（20.3.19），赋予其不同的含义：现在令 ${\mathcal{U}}_1$ 表示一种更新方法，该方法在代数上包含完整算子 $\mathcal{L}$ 的所有部分，但仅对 ${\mathcal{L}}_1$ 部分具有理想的稳定性；类似地定义 ${\mathcal{U}}_2,\dots ,{\mathcal{U}}_m$。那么从 $u^n$ 到 $u^{n+1}$ 的方法为：

$$\begin{array}{r}{u}^{n+1/m}={\mathcal{U}}_1(u^n,\Delta t/m)\\ u^{n+2/m}={\mathcal{U}}_2(u^{n+1/m},\Delta t/m)\\ \dots \end{array}$$

$$u^{n+1}={\mathcal{U}}_m(u^{n+(m-1)/m},\Delta t/m)$$

此时，(20.3.22) 中每个分数步长的时间步长仅为完整时间步长的 $1/m$，因为每个部分操作都作用于原始算子的所有项。

方程（20.3.22）通常（尽管并非总是）作为算子 $\mathcal{L}$ 的差分格式是稳定的。事实上，经验法则表明，通常只需对具有最高阶空间导数的算子部分保证 ${\mathcal{U}}_i$ 的稳定性——其余的 ${\mathcal{U}}_i$ 即使不稳定——整体格式也常常是稳定的！

至此，我们将注意力从初值问题转向边值问题。这些问题将占据本章剩余的大部分内容。

参考文献

Thomas, J.W. 1995, Numerical Partial Differential Equations: Finite Difference Methods (New York: Springer).

Ames, W.F. 1992, Numerical Methods for Partial Differential Equations, 3rd ed. (New York: Academic Press).

20.4 边值问题的傅里叶方法与循环约简方法

如 §20.0 所述，大多数边值问题（例如椭圆型方程）可归结为求解如下形式的大规模稀疏线性系统：

$$\mathbf{A}\cdot \mathbf{u}=\mathbf{b}$$

对于线性边值方程，只需求解一次；对于非线性边值方程，则需迭代求解。

当稀疏矩阵具有某些常见特殊结构时，有两种重要技术可“快速”求解方程（20.4.1）。当方程的系数在空间上为常数时，可直接应用傅里叶变换方法。循环约简方法则稍具一般性；其适用性与方程是否可分离（即是否满足“变量分离”条件）相关。这两种方法均要求边界与坐标线重合。最后，对某些问题，这两种方法可结合成一种更强大的方法，称为 FACR（傅里叶分析与循环约简）。下面我们依次讨论每种方法，并以方程（20.0.3）及其有限差分形式（20.0.6）作为模型示例。一般而言，本节所述方法在适用时，比 §20.5 中讨论的简单松弛法更快，但未必比 §20.6 中讨论的更复杂的多重网格法更快。

20.4.1 傅里叶变换方法

在 $x$ 和 $y$ 两个方向上的离散傅里叶逆变换为：

$$u_{jl}=\frac{1}{JL}\sum _{m=0}^{J-1}\sum _{n=0}^{L-1}{\hat{u}}_{mn}{e}^{-2\pi ijm/J}{e}^{-2\pi iln/L}$$

该变换可利用 FFT 在每个维度上独立计算，也可通过 §12.5 中的 four 例程或 §12.6 中的 r1ft3 例程一次性完成。类似地，

$${\rho }_{jl}=\frac{1}{JL}\sum _{m=0}^{J-1}\sum _{n=0}^{L-1}{\hat{\rho }}_{mn}{e}^{-2\pi ijm/J}{e}^{-2\pi iln/L}$$

若将表达式（20.4.2）和（20.4.3）代入我们的模型问题（20.0.6），可得：

$${\hat{u}}_{mn}\left(e^{2\pi im/J}+e^{-2\pi im/J}+e^{2\pi in/L}+e^{-2\pi in/L}-4\right)={\hat{\rho }}_{mn}{\Delta }^2$$

或

$${\hat{u}}_{mn}=\frac{{\hat{\rho }}_{mn}{\Delta }^2}{2\left(\cos \frac{2\pi m}{J}+\cos \frac{2\pi n}{L}-2\right)}$$

因此，利用 FFT 技术求解方程（20.0.6）的策略如下：

• 计算 ${\hat{\rho }}_{mn}$，即傅里叶变换：

$${\hat{\rho }}_{mn}=\sum _{j=0}^{J-1}\sum _{l=0}^{L-1}{\rho }_{jl}{e}^{2\pi imj/J}{e}^{2\pi inl/L}$$

• 利用方程（20.4.5）计算 ${\hat{u}}_{mn}$。

• 通过逆傅里叶变换（20.4.2）计算 $u_{jl}$。

上述过程适用于周期性边界条件。换言之，解满足：

$$u_{jl}=u_{j+J,l}=u_{j,l+L}$$

接下来考虑矩形边界上的 Dirichlet 边界条件 $u=0$。此时，我们不再使用展开式 (20.4.2)，而需要采用正弦波的展开形式：

$$u_{jl}=\frac{2}{J}\frac{2}{L}\sum _{m=1}^{J-1}\sum _{n=1}^{L-1}{\hat{u}}_{mn}\sin \frac{\pi jm}{J}\sin \frac{\pi ln}{L}$$

该展开式满足边界条件：在 $j=0,J$ 和 $l=0,L$ 处均有 $u=0$。若将此展开式以及 ${\rho }_{jl}$ 的类似展开式代入方程 (20.0.6)，则求解过程与周期性边界条件的情形类似：

• 通过正弦变换计算 ${\hat{\rho }}_{mn}$：

$${\hat{\rho }}_{mn}=\sum _{j=1}^{J-1}\sum _{l=1}^{L-1}{\rho }_{jl}\sin \frac{\pi jm}{J}\sin \frac{\pi ln}{L}$$

（§12.3 中给出了快速正弦变换算法。）

• 利用类似于 (20.4.5) 的表达式计算 ${\hat{u}}_{mn}$：

$${\hat{u}}_{mn}=\frac{{\Delta }^2{\hat{\rho }}_{mn}}{2\left(\cos \frac{\pi m}{J}+\cos \frac{\pi n}{L}-2\right)}$$

• 通过逆正弦变换 (20.4.8) 计算 $u_{jl}$。

如果边界条件是非齐次的，例如除边界 $x=J\Delta$ 上 $u=f(y)$ 外，其余边界上均为 $u=0$，则需在上述解的基础上再加上一个齐次方程

$$\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}=0$$

的解 $u^H$，使其满足所需的边界条件。在连续情形下，该解具有如下形式：

$$u^H=\sum _n{A}_n\sinh \frac{n\pi x}{L\Delta }\sin \frac{n\pi y}{L\Delta }$$

其中系数 $A_n$ 由边界条件 $u=f(y)$ 在 $x=J\Delta$ 处确定。在离散情形下，我们有

$$u_{jl}^H=\frac{2}{L}\sum _{n=1}^{L-1}{A}_n\sinh \frac{\pi nj}{L}\sin \frac{\pi nl}{L}$$

若记 $f(y=l\Delta )\equiv f_l$，则可通过如下逆公式求得 $A_n$：

$$A_n=\frac{1}{\sinh (\pi nJ/L)}\sum _{l=1}^{L-1}{f}_l\sin \frac{\pi nl}{L}$$

问题的完整解为

$$u=u_{jl}+u_{jl}^H$$

通过添加适当形式的项 (20.4.12)，我们可以处理任意边界面上的非齐次边界条件。

处理非齐次边界条件的一个更简单的方法是注意到：每当边界项出现在方程 (20.0.6) 的左边时，由于这些边界值已知，可将其移至右边。因此，有效源项为 ${\rho }_{jl}$ 加上来自边界项的贡献。为形式化地实现这一思想，将解写为

$$u=u^{\prime }+u^B$$

其中 $u^{\prime }$ 在边界上为零，而 $u^B$ 除边界外处处为零，在边界上取给定的边界值。在上述例子中，$u^B$ 的唯一非零值为

$$u_{J,l}^B=f_l$$

模型方程 (20.0.3) 变为

$${\nabla }^2{u}^{\prime }=-{\nabla }^2{u}^B+\rho$$

或其有限差分形式：

$$\begin{array}{rl}& u_{j+1,l}^{\prime }+u_{j-1,l}^{\prime }+u_{j,l+1}^{\prime }+u_{j,l-1}^{\prime }-4u_{j,l}^{\prime }=\\ & -(u_{j+1,l}^B+u_{j-1,l}^B+u_{j,l+1}^B+u_{j,l-1}^B-4u_{j,l}^B)+{\Delta }^2{\rho }_{j,l}\end{array}$$

在方程 (20.4.19) 中，所有 $u^B$ 项均为零，除非方程在 $j=J-1$ 处求值，此时有

$$u_{J,l}^{\prime }+u_{J-2,l}^{\prime }+u_{J-1,l+1}^{\prime }+u_{J-1,l-1}^{\prime }-4u_{J-1,l}^{\prime }=-f_l+{\Delta }^2{\rho }_{J-1,l}$$

因此，该问题现在等价于零边界条件的情形，只是源项中有一行被修改为：

$${\Delta }^2{\rho }_{J-1,l}\to {\Delta }^2{\rho }_{J-1,l}-f_l$$

对于 Neumann 边界条件 $\nabla u=0$，可采用余弦展开式 (12.4.11) 处理：

$$u_{jl}=\frac{2}{J}\frac{2}{L}\sum _{m=0}^J\sum _{n=0}^L{\hat{u}}_{mn}\cos \frac{\pi jm}{J}\cos \frac{\pi ln}{L}$$

此处的双撇号表示：当 $m=0$ 和 $m=J$ 时，对应的项应乘以 $\frac{1}{2}$；对 $n=0$ 和 $n=L$ 也类似处理。非齐次项 $\nabla u=g$ 可通过加上齐次方程的一个适当特解再次引入，或者更简单地将边界项移到方程右边。例如，边界条件

$$\frac{\partial u}{\partial x}=g(y)\mathrm{at}x=0$$

变为

$$\frac{u_{1,l}-u_{-1,l}}{2\Delta }=g_l$$

其中 $g_l\equiv g(y=l\Delta )$。我们再次将解写成 (20.4.16) 的形式，其中现在边界上满足 $\nabla u^{\prime }=0$。这一次，$\nabla u^B$ 在边界上取给定值，但 $u^B$ 除边界外处处为零。因此，方程 (20.4.24) 给出

$$u_{-1,l}^B=-2\Delta g_l$$

在方程 (20.4.19) 中，所有 $u^B$ 项除 $j=0$ 外均为零：

$$u_{1,l}^{\prime }+u_{-1,l}^{\prime }+u_{0,l+1}^{\prime }+u_{0,l-1}^{\prime }-4u_{0,l}^{\prime }=2\Delta g_l+{\Delta }^2{\rho }_{0,l}$$

因此，$u^{\prime }$ 是一个零梯度问题的解，其源项被修改为：

$${\Delta }^2{\rho }_{0,l}\to {\Delta }^2{\rho }_{0,l}+2\Delta g_l$$

有时，Neumann 边界条件通过使用交错网格来处理，即将 $u$ 定义在网格单元边界之间的中点，使得一阶导数在网格点上居中。如果你使用余弦变换的另一种形式（即方程 (12.4.17)），就可以用类似于上述的技术来求解这类问题。

20.4.2 循环约简法（Cyclic Reduction）

显然，FFT 方法仅适用于原始偏微分方程具有常系数、且边界与坐标线重合的情形。另一种可用于稍更一般方程的算法称为循环约简法（Cyclic Reduction, CR）。

我们以如下方程为例说明循环约简法：

$$\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}+b(y)\frac{\partial u}{\partial y}+c(y)u=g(x,y)$$

这种形式在实践中经常出现，例如在极坐标、柱坐标或球坐标系下由 Helmholtz 方程或 Poisson 方程导出。更一般的可分离变量方程见文献 [1]。

方程 (20.4.28) 的有限差分形式可写成一组向量方程：

$${\mathbf{u}}_{j-1}+\mathbf{T}\cdot {\mathbf{u}}_j+{\mathbf{u}}_{j+1}={\mathbf{g}}_j{\Delta }^2$$

这里下标 $j$ 来自 $x$ 方向的差分，而 $y$ 方向的差分（之前用下标 $l$ 表示）仍保留为向量形式。矩阵 $\mathbf{T}$ 具有如下形式：

$$\mathbf{T}=\mathbf{B}-2\mathbf{I}$$

其中的 $2$ 来自 $x$ 方向的差分，矩阵 $\mathbf{B}$ 来自 $y$ 方向的差分。矩阵 $\mathbf{B}$（从而 $\mathbf{T}$）是一个具有变系数的三对角矩阵。

CR 方法的推导过程如下：写出三个连续的类似于 (20.4.29) 的方程：

$$\begin{array}{r}{\mathbf{u}}_{j-2}+\mathbf{T}\cdot {\mathbf{u}}_{j-1}+{\mathbf{u}}_j={\mathbf{g}}_{j-1}{\Delta }^2\\ {\mathbf{u}}_{j-1}+\mathbf{T}\cdot {\mathbf{u}}_j+{\mathbf{u}}_{j+1}={\mathbf{g}}_j{\Delta }^2\\ {\mathbf{u}}_j+\mathbf{T}\cdot {\mathbf{u}}_{j+1}+{\mathbf{u}}_{j+2}={\mathbf{g}}_{j+1}{\Delta }^2\end{array}$$

将中间方程左乘 $-\mathbf{T}$，然后将三个方程相加，得到：

$${\mathbf{u}}_{j-2}+{\mathbf{T}}^{(1)}\cdot {\mathbf{u}}_j+{\mathbf{u}}_{j+2}={\mathbf{g}}_j^{(1)}{\Delta }^2$$

这是一个与 (20.4.29) 形式相同的方程，其中

$$\begin{array}{r}{\mathbf{T}}^{(1)}=21-{\mathbf{T}}^2\\ {\mathbf{g}}_i^{(1)}={\Delta }^2({\mathbf{g}}_{j-1}-\mathbf{T}\cdot {\mathbf{g}}_j+{\mathbf{g}}_{j+1})\end{array}$$

经过一次循环约简（CR）后，方程数量减少为原来的一半。由于所得方程与原始方程具有相同的形式，我们可以重复这一过程。为简化起见，假设网格点数为 2 的幂次，最终我们得到一个关于变量中心线的单一方程：

$${\mathbf{T}}^{(f)}\cdot {\mathbf{u}}_{J/2}={\Delta }^2{\mathbf{g}}_{J/2}^{(f)}-{\mathbf{u}}_0-{\mathbf{u}}_J$$

这里我们将 ${\mathbf{u}}_0$ 和 ${\mathbf{u}}_J$ 移到了等式右边，因为它们是已知的边界值。方程 (20.4.34) 可通过标准的三对角矩阵算法求解 ${\mathbf{u}}_{J/2}$。在第 $f-1$ 层的两个方程分别涉及 ${\mathbf{u}}_{J/4}$ 和 ${\mathbf{u}}_{3J/4}$。其中关于 ${\mathbf{u}}_{J/4}$ 的方程包含 ${\mathbf{u}}_0$ 和 ${\mathbf{u}}_{J/2}$，二者均已知，因此也可用常规的三对角求解程序求解。类似的情况在每一阶段都成立，因此我们最终需要求解 $J-1$ 个三对角方程组。

在实际应用中，为避免数值不稳定，应对方程 (20.4.33) 进行改写。有关这些及其他实际细节，请参见文献 [2]。

20.4.3 FACR 方法

求解形如 (20.4.28) 的方程（包括常系数问题 (20.0.3)）的最佳方法是将傅里叶分析与循环约简相结合，即 FACR 方法 [3–6]。若在 CR 的第 $r$ 阶段，我们沿 $y$ 方向对形如 (20.4.32) 的方程进行傅里叶分析（即对被省略的向量指标进行分析），则对每个 $y$ 方向的傅里叶模态，都会得到一个 $x$ 方向的三对角方程组：

$${\hat{u}}_{i-2r}^k+{\lambda }_k^{(r)}{\hat{u}}_i^k+{\hat{u}}_{i+2r}^k={\Delta }^2{g}_i^{(r)k}$$

此处 ${\lambda }_k^{(r)}$ 是 ${\mathbf{T}}^{(r)}$ 对应于第 $k$ 个傅里叶模态的特征值。对于方程 (20.0.3)，由方程 (20.4.5) 可知，${\lambda }_k^{(r)}$ 将包含形如 $\cos (2\pi k/L)-2$ 的项的幂次。在层级 $j=2^r$、$2\times 2^r$、$4\times 2^r$、…、$J-2^r$ 上求解 ${\hat{\mathbf{u}}}_j^k$ 的三对角方程组，再通过傅里叶合成得到这些 $x$ 线上的 $y$ 值。然后按照原始 CR 算法填充中间的 $x$ 线。

关键在于选择适当的 CR 层数，以最小化总的算术运算量。可以证明，对于典型的 128×128 网格，最优层数为 $r=2$；在渐近情况下，$r\to \log (\log J)$。

对于方程 (20.0.3)，这些算法的大致运行时间估计如下：全 FFT 方法（在 $x$ 和 $y$ 两个方向）与 CR 方法大致相当。当 $r=0$ 时的 FACR 方法（即在一个方向使用 FFT，另一方向用常规算法求解三对角方程组）可获得约两倍的速度提升。而当 $r=2$ 时的最优 FACR 方法可在此基础上再获得约两倍的速度提升。

参考文献

Swartzrauber, P.N. 1977, "The Methods of Cyclic Reduction, Fourier Analysis and the FACR Algorithm for the Discrete Solution of Poisson's Equation on a Rectangle," SIAM Review, vol. 19, pp. 490–501.[1]

Buzbee, B.L., Golub, G.H., and Nielson, C.W. 1970, "On Direct Methods for Solving Poisson's Equation," SIAM Journal on Numerical Analysis, vol. 7, pp. 627–656; see also op. cit. vol. 11, pp. 753–763.[2]

Hockney, R.W. 1965, "A Fast Direct Solution of Poisson's Equation Using Fourier Analysis," Journal of the Association for Computing Machinery, vol. 12, pp. 95–113.[3]

Hockney, R.W. 1970, "The Potential Calculation and Some Applications," Methods of Computational Physics, vol. 9 (New York: Academic Press), pp. 135–211.[4]

Hockney, R.W., and Eastwood, J.W. 1981, Computer Simulation Using Particles (New York: McGraw-Hill), Chapter 6.[5]

Tempterton, C. 1980, "On the FACR Algorithm for the Discrete Poisson Equation," Journal of Computational Physics, vol. 34, pp. 314–329.[6]

20.5 边值问题的松弛方法

正如我们在 §20.0 中提到的，松弛方法涉及对由有限差分产生的稀疏矩阵进行分裂，然后迭代直至找到解。

还有一种对松弛方法的理解方式更具物理直观性。假设我们希望求解椭圆型方程

$$\mathcal{L}u=\rho$$

其中 $\mathcal{L}$ 表示某个椭圆算子，$\rho$ 为源项。将该方程改写为扩散方程：

$$\frac{\partial u}{\partial t}=\mathcal{L}u-\rho$$

初始分布 $u$ 随时间 $t\to \infty$ 趋于平衡解。该平衡态下所有时间导数为零，因此即为原椭圆问题 (20.5.1) 的解。由此可见，§20.2 中关于扩散型初值问题的所有方法均可用于通过松弛方法求解边值问题。

我们将这一思想应用于模型问题 (20.0.3)。对应的扩散方程为

$$\frac{\partial u}{\partial t}=\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}-\rho$$

若采用 FTCS 差分格式（参见方程 20.2.4），可得

$$u_{j,l}^{n+1}=u_{j,l}^n+\frac{\Delta t}{{\Delta }^2}\left(u_{j+1,l}^n+u_{j-1,l}^n+u_{j,l+1}^n+u_{j,l-1}^n-4u_{j,l}^n\right)-{\rho }_{j,l}\Delta t$$

由 (20.2.6) 可知，FTCS 差分格式在一维空间中稳定的条件是 $\Delta t/{\Delta }^2\le \frac{1}{2}$。在二维情况下，该条件变为 $\Delta t/{\Delta }^2\le \frac{1}{4}$。假设我们取尽可能大的时间步长，令 $\Delta t={\Delta }^2/4$，则方程 (20.5.4) 变为

$$u_{j,l}^{n+1}=\frac{1}{4}\left(u_{j+1,l}^n+u_{j-1,l}^n+u_{j,l+1}^n+u_{j,l-1}^n\right)-\frac{{\Delta }^2}{4}{\rho }_{j,l}$$

因此，该算法通过取网格上四个最近邻点处 $u$ 的平均值（再加上源项的贡献）来更新 $u$。然后重复此过程直至收敛。

这种方法实际上是一种经典方法，其起源可追溯到上个世纪，称为雅可比（Jacobi）方法（注意不要与用于求解特征值的雅可比方法混淆）。该方法并不实用，因为其收敛速度太慢。然而，它是理解现代方法的基础，现代方法总是与之进行比较。

另一种经典方法是高斯-赛德尔（Gauss-Seidel）方法，该方法在多重网格法（§20.6）中具有重要意义。这里，我们一旦获得 $u$ 的更新值，就立即在公式 (20.5.5) 的右侧使用这些新值。换句话说，平均操作是“原地”进行的，而不是从一个时间步“复制”到下一个时间步。如果我们沿行方向进行迭代，对固定的 $l$ 递增 $j$，则有：

$$u_{j,l}^{n+1}=\frac{1}{4}\left(u_{j+1,l}^n+u_{j-1,l}^{n+1}+u_{j,l+1}^n+u_{j,l-1}^{n+1}\right)-\frac{{\Delta }^2}{4}{\rho }_{j,l}$$

该方法本身收敛也很慢，仅具有理论意义，但对其做一些分析将很有启发性。

让我们从矩阵分裂的角度来看雅可比方法和高斯-赛德尔方法。我们改变记号，将 $\mathbf{u}$ 记为 “$\mathbf{x}$”，以符合标准矩阵记号。为求解

$$\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$$

我们可以将 $\mathbf{A}$ 分裂为

$$\mathbf{A}=\mathbf{L}+\mathbf{D}+\mathbf{U}$$

其中 $\mathbf{D}$ 是 $\mathbf{A}$ 的对角部分，$\mathbf{L}$ 是 $\mathbf{A}$ 的严格下三角部分（对角线元素为零），$\mathbf{U}$ 是 $\mathbf{A}$ 的严格上三角部分（对角线元素为零）。

在雅可比方法中，第 $r$ 步迭代写作

$$\mathbf{D}\cdot {\mathbf{x}}^{(r)}=-(\mathbf{L}+\mathbf{U})\cdot {\mathbf{x}}^{(r-1)}+\mathbf{b}$$

对于我们的模型问题 (20.5.5)，$\mathbf{D}$ 就是单位矩阵。当矩阵 $\mathbf{A}$ 在某种可严格数学定义的意义下“对角占优”时，雅可比方法收敛。对于由有限差分导出的矩阵，这一条件通常满足。

雅可比方法的收敛速率如何？详细分析超出了我们的范围，但可以简要说明如下：矩阵 $-{\mathbf{D}}^{-1}\cdot (\mathbf{L}+\mathbf{U})$ 是迭代矩阵，它（忽略一个加性项）将一组 $\mathbf{x}$ 映射到下一组。该迭代矩阵具有特征值，每个特征值反映了在一次迭代中某个特定误差特征模态的振幅被抑制的因子。显然，要使松弛过程有效，所有这些因子的模必须小于 1！

该方法的收敛速率由衰减最慢的特征模态决定，即具有最大模的因子。这个最大因子的模（介于 0 和 1 之间）称为松弛算子的谱半径，记为 ${\rho }_s$。

因此，将整体误差减少 $10^{-p}$ 倍所需的迭代次数 $r$ 可估计为

$$r\approx \frac{p\ln 10}{(-\ln {\rho }_s)}$$

通常，当网格尺寸 $J$ 增大时，谱半径 ${\rho }_s$ 渐近趋于 1，因此需要更多的迭代次数。对于任意给定的方程、网格几何结构和边界条件，原则上可以解析计算谱半径。例如，对于方程 (20.5.5)，在 $J\times J$ 网格上且四边均为狄利克雷（Dirichlet）边界条件的情形，当 $J$ 很大时，其渐近公式为

$${\rho }_s\simeq 1-\frac{{\pi }^2}{2J^2}$$

因此，将误差减少 $10^{-p}$ 倍所需的迭代次数为

$$r\simeq \frac{2p{J}^2\ln 10}{{\pi }^2}\simeq \frac{1}{2}p{J}^2$$

换句话说，迭代次数与网格点数 $J^2$ 成正比。由于 $100\times 100$ 甚至更大的问题很常见，显然雅可比方法仅具有理论意义。

高斯-赛德尔方法，即公式 (20.5.6)，对应于如下矩阵分解：

$$(\mathbf{L}+\mathbf{D})\cdot {\mathbf{x}}^{(r)}=-\mathbf{U}\cdot {\mathbf{x}}^{(r-1)}+\mathbf{b}$$

方程左侧出现 $\mathbf{L}$ 是由于原地更新所致，这一点在将 (20.5.13) 按分量展开后很容易验证。可以证明 [1-3]，其谱半径恰好是雅可比方法谱半径的平方。因此，对于我们的模型问题，

$${\rho }_s\simeq 1-\frac{{\pi }^2}{J^2}$$

$$r\simeq \frac{p{J}^2\ln 10}{{\pi }^2}\simeq \frac{1}{4}p{J}^2$$

尽管迭代次数相比雅可比方法减少了一半，但该方法仍然不实用。

20.5.1 逐次超松弛法（SOR）

如果我们对高斯-赛德尔迭代第 $r$ 步中的 ${\mathbf{x}}^{(r)}$ 值进行“过度校正”（overcorrection），从而提前预估未来的修正量，就能得到一个更好的算法——该算法在 1970 年代之前一直是标准算法。将 (20.5.13) 式解出 ${\mathbf{x}}^{(r)}$，并在右侧加上再减去 ${\mathbf{x}}^{(r-1)}$，即可将高斯-赛德尔方法写成如下形式：

$${\mathbf{x}}^{(r)}={\mathbf{x}}^{(r-1)}-(\mathbf{L}+\mathbf{D}{)}^{-1}\cdot [(\mathbf{L}+\mathbf{D}+\mathbf{U})\cdot {\mathbf{x}}^{(r-1)}-\mathbf{b}]$$

方括号中的项正是残差向量 ${\mathbf{\xi }}^{(r-1)}$，因此有：

$${\mathbf{x}}^{(r)}={\mathbf{x}}^{(r-1)}-(\mathbf{L}+\mathbf{D}{)}^{-1}\cdot {\mathbf{\xi }}^{(r-1)}$$

现在我们进行过度校正，定义：

$${\mathbf{x}}^{(r)}={\mathbf{x}}^{(r-1)}-\omega (\mathbf{L}+\mathbf{D}{)}^{-1}\cdot {\mathbf{\xi }}^{(r-1)}$$

其中 $\omega$ 被称为超松弛参数（overrelaxation parameter），该方法称为逐次超松弛法（Successive Overrelaxation, SOR）。

以下定理可以被证明 [1–3]：

• 该方法仅当 $0<\omega <2$ 时收敛。若 $0<\omega <1$，则称为欠松弛（underrelaxation）。
• 在某些通常由有限差分法产生的矩阵所满足的数学条件下，只有超松弛（即 $1<\omega <2$）才能比高斯-赛德尔方法获得更快的收敛速度。
• 若 ${\rho }_{\mathrm{Jacobi}}$ 是雅可比迭代的谱半径（因此其平方即为高斯-赛德尔迭代的谱半径），则最优的 $\omega$ 选择为：

$$\omega =\frac{2}{1+\sqrt{1-{\rho }_{\mathrm{Jacobi}}^2}}$$

• 对于该最优选择，SOR 的谱半径为：

$${\rho }_{\mathrm{SOR}}={\left(\frac{{\rho }_{\mathrm{Jacobi}}}{1+\sqrt{1-{\rho }_{\mathrm{Jacobi}}^2}}\right)}^2$$

作为上述结果的一个应用，考虑我们的模型问题，其中 ${\rho }_{\mathrm{Jacobi}}$ 由方程 (20.5.11) 给出。于是方程 (20.5.19) 和 (20.5.20) 给出：

$$\omega \simeq \frac{2}{1+\pi /J}$$

$${\rho }_{\mathrm{SOR}}\simeq 1-\frac{2\pi }{J}\text{当 }J\text{ 很大时}$$

方程 (20.5.10) 给出了将初始误差减少 $10^{-p}$ 倍所需的迭代次数：

$$r\simeq \frac{pJ\ln 10}{2\pi }\simeq \frac{1}{3}pJ$$

与方程 (20.5.12) 或 (20.5.15) 相比，我们发现最优 SOR 所需的迭代次数为 $J$ 阶，而非 $J^2$ 阶。由于 $J$ 通常为 100 或更大，这带来了巨大的差异！方程 (20.5.23) 还引出了一个便于记忆的经验法则：三位有效数字的精度（$p=3$）所需的迭代次数大致等于网格一边上的网格点数；若要达到六位有效数字的精度，则大约需要两倍的迭代次数。

那么，对于一个无法解析求得最优 $\omega$ 的问题，我们该如何选择 $\omega$ 呢？这正是 SOR 方法的弱点所在！SOR 的优势仅在最优 $\omega$ 值附近一个相当窄的窗口内才能体现。宁可将 $\omega$ 取得略大一些，也不要略小，但最好是准确取到最优值。

一种选择 $\omega$ 的方法是将你的问题近似地映射到一个已知的问题上，用平均值代替方程中的系数。但请注意，这个已知问题必须与实际问题具有相同的网格尺寸和边界条件。为便于参考，我们给出矩形 $J\times L$ 网格上模型问题的 ${\rho }_{\mathrm{Jacobi}}$ 值（允许 $\Delta x\ne \Delta y$）：

$${\rho }_{\mathrm{Jacobi}}=\frac{\cos \frac{\pi }{J}+{\left(\frac{\Delta x}{\Delta y}\right)}^2\cos \frac{\pi }{L}}{1+{\left(\frac{\Delta x}{\Delta y}\right)}^2}$$

方程 (20.5.24) 适用于齐次 Dirichlet 或 Neumann 边界条件。对于周期性边界条件，需将 $\pi$ 替换为 $2\pi$。

第二种方法特别适用于需要反复求解多个系数略有不同的椭圆型方程的情形：先对第一个方程通过实验确定最优 $\omega$ 值，然后将其用于后续方程。文献中描述了多种自动确定最优 $\omega$ 值的方案，以及“搜索”最佳 $\omega$ 值的方法。

虽然前面引入的矩阵记号对理论分析很有帮助，但在实际实现 SOR 算法时，我们需要显式的公式。考虑一个关于 $x$ 和 $y$ 的一般二阶椭圆型方程，像我们的模型方程一样在正方形网格上进行有限差分离散。矩阵 $\mathbf{A}$ 的每一行对应如下形式的方程：

$$a_{i,l}{u}_{i+1,l}+b_{i,l}{u}_{i-1,l}+c_{i,l}{u}_{i,l+1}+d_{i,l}{u}_{i,l-1}+e_{i,l}{u}_{i,l}=f_{i,l}$$

对于我们的模型方程，有 $a=b=c=d=1,e=-4$。量 $f$ 与源项成正比。迭代过程通过将 (20.5.25) 式解出 $u_{i,l}$ 来定义：

$$u_{i,l}^{\ast }=\frac{1}{e_{i,l}}\left(f_{i,l}-a_{i,l}{u}_{i+1,l}-b_{i,l}{u}_{i-1,l}-c_{i,l}{u}_{i,l+1}-d_{i,l}{u}_{i,l-1}\right)$$

然后 $u_{i,l}^{\mathrm{new}}$ 是一个加权平均，

$$u_{i,l}^{\mathrm{new}}=\omega u_{j,l}^{\ast }+(1-\omega )u_{i,l}^{\mathrm{old}}$$

我们按如下方式计算：任意阶段的残差为

$${\xi }_{j,l}=a_{i,l}{u}_{j+1,l}+b_{i,l}{u}_{j-1,l}+c_{j,l}{u}_{j,l+1}+d_{j,l}{u}_{j,l-1}+e_{j,l}{u}_{i,l}-f_{i,l}$$

而 SOR 算法（20.5.18）或（20.5.27）为

$$u_{j,l}^{\mathrm{new}}=u_{j,l}^{\mathrm{old}}-\omega \frac{{\xi }_{j,l}}{e_{j,l}}$$

这种形式非常易于编程，且残差向量 ${\xi }_{j,l}$ 的范数可用作迭代终止的判据。

另一个实际问题涉及网格点的处理顺序。最直接的策略就是简单地按行（或列）顺序依次处理。

另一种方法是将网格划分为“奇数”和“偶数”网格，类似于国际象棋棋盘上的红黑方格。此时方程（20.5.26）表明，奇数点仅依赖于偶数网格的值，反之亦然。因此，我们可以先进行半次扫描更新所有奇数点，然后再进行另一次半扫描，利用更新后的奇数点值来更新偶数点。对于下面实现的 SOR 版本，我们将采用奇偶排序（odd-even ordering）。

最后一个实际问题是，在实践中，SOR 的渐近收敛速率通常要经过大约 $J$ 次迭代后才能达到。在收敛开始之前，误差常常会增大到原来的 20 倍。对 SOR 稍作修改即可解决此问题。该修改基于如下观察：虽然 $\omega$ 是最优的渐近松弛参数，但它未必是初始阶段的良好选择。在采用切比雪夫加速（Chebyshev acceleration）的 SOR 方法中，我们使用奇偶排序，并在每次半扫描时根据以下规则更新 $\omega$：

$$\begin{array}{rl}& {\omega }^{(0)}=1\\ & {\omega }^{(1/2)}=1/(1-{\rho }_{\mathrm{Jacobi}}^2/2)\\ & {\omega }^{(n+1/2)}=1/(1-{\rho }_{\mathrm{Jacobi}}^2{\omega }^{(n)}/4),n=1/2,1,\dots ,\infty \\ & {\omega }^{(\infty )}\to {\omega }_{\mathrm{optimal}}\end{array}$$

切比雪夫加速的优点在于，每次迭代后误差的范数总是单调递减的。（这里指的是 $u_{j,l}$ 的实际误差范数；而残差 ${\xi }_{j,l}$ 的范数则未必单调递减。）尽管其渐近收敛速率与普通 SOR 相同，但没有任何理由不使用切比雪夫加速来减少所需的总迭代次数。

下面给出一个带切比雪夫加速的 SOR 算法例程。

void sor(MatDoub_I &a, MatDoub_I &b, MatDoub_I &c, MatDoub_I &d, MatDoub_I &e, MatDoub_I &f, MatDoub_IO &u, const Doub RJac)

使用切比雪夫加速的逐次超松弛法（SOR）求解方程（20.5.25）。输入参数 a、b、c、d、e 和 f 为方程的系数，其维度均为网格大小 [0..jmax-1][0..jmax-1]。u 作为解的初始猜测值输入（通常为零），并返回最终结果。RJac 为雅可比迭代的谱半径或其估计值。

{
    const Int MAXITS = 1000;
    const Doub EPS = 1.0e-13;
    Doub anormf = 0.0, omega = 1.0;
    Int jmax = a.nrows();
    for (Int j = 1; j < jmax - 1; j++)
        // 计算初始残差范数，并在范数减小到 EPS 倍时终止迭代。
        for (Int l = 1; l < jmax - 1; l++)
            anormf += abs(f[j][l]);
    for (Int n = 0; n < MAXITS; n++) {
        Doub anorm = 0.0;
        Int jsw = 1;
        for (Int ipass = 0; ipass < 2; ipass++) {
            Int lsw = jsw;
            for (Int j = 1; j < jmax - 1; j++) {
                for (Int l = lsw; l < jmax - 1; l += 2) {
                    Doub resid = a[j][l] * u[j + 1][l] + b[j][l] * u[j - 1][l]
                               + c[j][l] * u[j][l + 1] + d[j][l] * u[j][l - 1]
                               + e[j][l] * u[j][l] - f[j][l];
                    anorm += abs(resid);
                    u[j][l] -= omega * resid / e[j][l];
                }
            }
            lsw = 3 - lsw;
        }
        jsw = 3 - jsw;
        omega = (n == 0 && ipass == 0 ? 1.0 / (1.0 - 0.5 * RJac * RJac) 
                                      : 1.0 / (1.0 - 0.25 * RJac * RJac * omega));
        if (anorm < EPS * anormf) return;
    }
    throw("MAXITS exceeded");
}

SOR 的主要优点是编程非常简单；其主要缺点是在大规模问题上仍然效率很低。

20.5.2 ADI（交替方向隐式）方法

§20.3 中用于扩散方程的 ADI 方法可转化为椭圆型方程的松弛方法 [1–4]。在 §20.3 中，我们讨论了 ADI 作为求解含时热传导方程的方法：

$$\frac{\partial u}{\partial t}={\nabla }^{2}u-\rho$$

令 $t\to \infty$，即可得到求解椭圆型方程

$${\nabla }^{2}u=\rho$$

的迭代方法。

无论哪种情况，算子分裂的形式均为

$$\mathcal{L}={\mathcal{L}}_x+{\mathcal{L}}_y$$

其中 ${\mathcal{L}}_x$ 表示 $x$ 方向的差分算子，${\mathcal{L}}_y$ 表示 $y$ 方向的差分算子。

例如，在我们的模型问题（20.0.6）中，若 $\Delta x=\Delta y=\Delta$，则有

$$\begin{array}{r}{\mathcal{L}}_{x}u=2u_{j,l}-u_{j+1,l}-u_{j-1,l}\\ {\mathcal{L}}_{y}u=2u_{j,l}-u_{j,l+1}-u_{j,l-1}\end{array}$$

更复杂的算子也可以类似地进行分裂，但这需要一定的技巧。不恰当的分裂可能导致算法无法收敛。通常，人们会根据问题的物理本质来设计分裂方式。对于我们的模型问题，我们知道初始瞬态会逐渐扩散消失，因此我们设置 $x$ 和 $y$ 方向的分裂以模拟每个维度上的扩散过程。

选定分裂方式后，我们将含时方程（20.5.31）在两个半步长内隐式差分：

$$\begin{array}{r}\frac{u^{n+1/2}-u^n}{\Delta t/2}=-\frac{{\mathcal{L}}_x{u}^{n+1/2}+{\mathcal{L}}_y{u}^n}{{\Delta }^2}-\rho \\ \frac{u^{n+1}-u^{n+1/2}}{\Delta t/2}=-\frac{{\mathcal{L}}_x{u}^{n+1/2}+{\mathcal{L}}_y{u}^{n+1}}{{\Delta }^2}-\rho \end{array}$$

（参见公式 20.3.16）。此处我们省略了空间指标 $(j,l)$。用矩阵形式表示，方程 (20.5.35) 为：

$$({\mathbf{L}}_x+r1)\cdot {\mathbf{u}}^{n+1/2}=(r1-{\mathbf{L}}_y)\cdot {\mathbf{u}}^n-{\Delta }^2\rho$$

$$({\mathbf{L}}_y+r1)\cdot {\mathbf{u}}^{n+1}=(r1-{\mathbf{L}}_x)\cdot {\mathbf{u}}^{n+1/2}-{\Delta }^2\rho$$

其中

$$r\equiv \frac{2{\Delta }^2}{\Delta t}$$

方程 (20.5.36) 和 (20.5.37) 左边的矩阵是三对角矩阵（通常还是正定的），因此可以用标准的三对角矩阵算法求解。给定 ${\mathbf{u}}^n$，先求解 (20.5.36) 得到 ${\mathbf{u}}^{n+1/2}$，将其代入 (20.5.37) 的右边，再求解得到 ${\mathbf{u}}^{n+1}$。关键问题是如何选择迭代参数 $r$，这类似于初值问题中对时间步长的选择。

通常，我们的目标是最小化迭代矩阵的谱半径。虽然此处不展开细节，但可以指出：对于最优的 $r$ 选择，ADI 方法具有与 SOR 方法相同的收敛速率。然而，ADI 方法中的单次迭代步骤比 SOR 复杂得多，因此表面上看 ADI 方法似乎更差。如果每次迭代都使用相同的参数 $r$，这确实是事实。然而，我们也可以为每次迭代选择不同的 $r$。若能最优地进行这种选择，ADI 方法通常会比 SOR 更高效。具体细节请参阅文献 [1–4]。

我们在此未完整实现 ADI 方法的原因是，在大多数应用中，它已被下一节所述的多重网格法所取代。我们的建议是：对于简单问题（例如 $30\times 30$ 网格）或只需对较大问题求解一次的情形，可使用 SOR 方法，因为此时编程简便性比计算时间开销更重要。偶尔，§2.7 中的稀疏矩阵方法也可用于直接求解差分方程组。然而，对于大规模椭圆型问题的常规求解，多重网格法如今几乎总是首选方法。

参考文献

Hockney, R.W., and Eastwood, J.W. 1981, Computer Simulation Using Particles (New York: McGraw-Hill), Chapter 6.

Young, D.M. 1971, Iterative Solution of Large Linear Systems (New York: Academic Press); reprinted 2003 (New York: Dover).[1]

Stoer, J., and Bulirsch, R. 2002, Introduction to Numerical Analysis, 3rd ed. (New York: Springer), §8.3 – §8.6.[2]

Varga, R.S. 2000, Matrix Iterative Analysis, 2nd ed. (New York: Springer).[3]

Spanier, J. 1967, in Mathematical Methods for Digital Computers, Volume 2 (New York: Wiley), Chapter 11.[4]

20.6 边值问题的多重网格法

实用的多重网格法最早由 Brandt [1,2] 在 20 世纪 70 年代提出。这些方法可以在 $O(N)$ 次运算内求解在 $N$ 个网格点上离散化的椭圆型偏微分方程。“快速”直接椭圆求解器（见 §20.4）可在 $O(N\log N)$ 次运算内求解某些特殊类型的椭圆方程。这些估计中的数值系数使得多重网格法在执行速度上与快速方法相当。然而，与快速方法不同的是，多重网格法几乎不会因效率损失而能够求解具有非常数系数的一般椭圆方程，甚至非线性方程也能以相近的速度求解。

遗憾的是，并不存在一种能求解所有椭圆问题的单一多重网格算法。实际上，多重网格是一种提供求解框架的技术，你必须在此框架内调整算法的各个组成部分，以适应你的具体问题。我们在此只能对该主题作简要介绍。特别地，我们将给出两个多重网格例程示例，一个线性，一个非线性。通过参考这些原型并查阅文献 [3–6]，你应该能够开发出求解自身问题的程序。

多重网格技术有两种相关但不同的应用方式。第一种称为多重网格法（multigrid method），用于加速传统松弛方法在预先指定精细度的网格上的收敛。在这种情况下，你只需在此网格上定义你的问题（例如计算源项）。该方法定义的其他更粗的网格可视为临时的计算辅助工具。

第二种方法（可能有些令人困惑地）称为完全多重网格法（full multigrid, FMG），要求你能够在不同尺度的网格上定义你的问题（通常是将同一底层偏微分方程离散化为不同规模的有限差分方程组）。在这种方法中，算法在越来越细的网格上依次获得解。你可以在达到预设的网格精细度时停止计算，也可以监测离散化引起的截断误差，仅当误差足够小时才停止。

本节将首先讨论多重网格法，然后利用所发展的概念引入 FMG 方法。后一种算法是我们随附程序中所实现的方法。

20.6.1 从单网格、双网格到多重网格

多重网格法的核心思想可通过最简单的双网格方法来理解。假设我们试图求解线性椭圆问题：

$$\mathcal{L}u=f$$

其中 $\mathcal{L}$ 是某个线性椭圆算子，$f$ 是源项。在网格步长为 $h$ 的均匀网格上离散化方程 (20.6.1)，得到的线性代数方程组可写作：

$${\mathcal{L}}_h{\mathcal{U}}_h=f_h$$

令 ${\tilde{u}}_h$ 表示方程 (20.6.2) 的某个近似解。我们将 $u_h$ 记为差分方程 (20.6.2) 的精确解。则 ${\tilde{u}}_h$ 的误差（或修正量）为：

$${\mathbf{v}}_h={\mathbf{u}}_h-{\tilde{\mathbf{u}}}_h$$

残差（或缺陷）为：

$$d_h={\mathcal{L}}_h{\tilde{u}}_h-f_h$$

（注意：有些作者将残差定义为负的缺陷，对于公式 20.6.4 定义的是这两个量中的哪一个，并没有统一的共识。）由于 ${\mathcal{L}}_h$ 是线性的，误差满足

$${\mathcal{L}}_h{v}_h=-d_h$$

此时，我们需要对 ${\mathcal{L}}_h$ 做一个近似，以便求出 $v_h$。经典的迭代方法（如 Jacobi 或 Gauss-Seidel 方法）在每一步通过求解如下方程的近似解来实现这一点：

$${\hat{\mathcal{L}}}_h{\hat{v}}_h=-d_h$$

其中 ${\hat{\mathcal{L}}}_h$ 是比 ${\mathcal{L}}_h$ “更简单”的算子。例如，在 Jacobi 迭代中，${\hat{\mathcal{L}}}_h$ 是 ${\mathcal{L}}_h$ 的对角部分；而在 Gauss-Seidel 迭代中，它是下三角部分。下一步近似解由下式生成：

$${\tilde{u}}_h^{\mathrm{new}}={\tilde{u}}_h+{\hat{v}}_h$$

现在，我们考虑另一种完全不同的 ${\mathcal{L}}_h$ 近似方式，即“粗化”（coarsify）而非“简化”（simplify）。也就是说，我们在一个网格步长为 $H$ 的粗网格上构造 ${\mathcal{L}}_h$ 的某种适当近似 ${\mathcal{L}}_H$（我们通常取 $H=2h$，但也可以有其他选择）。此时，残差方程 (20.6.5) 被近似为：

$${\mathcal{L}}_H{v}_H=-d_H$$

由于 ${\mathcal{L}}_H$ 的维数更小，该方程比方程 (20.6.5) 更容易求解。为了在粗网格上定义缺陷 $d_H$，我们需要一个限制算子 $\mathcal{R}$，将 $d_h$ 限制到粗网格上：

$$d_H=\mathcal{R}{d}_h$$

该限制算子也称为细到粗算子（fine-to-coarse operator）或注入算子（injection operator）。一旦我们得到了方程 (20.6.8) 的解 ${\tilde{v}}_H$，就需要一个延拓算子 $\mathcal{P}$，将校正量延拓（或插值）回细网格：

$${\tilde{v}}_h=\mathcal{P}{\tilde{v}}_H$$

该延拓算子也称为粗到细算子（coarse-to-fine operator）或插值算子（interpolation operator）。$\mathcal{R}$ 和 $\mathcal{P}$ 均被选为线性算子。最后，近似解 ${\tilde{\mathbf{\tau }}}_h$ 可按如下步骤更新：

• 通过 (20.6.9) 限制缺陷。
• 在粗网格上精确求解 (20.6.8) 得到校正量。
• 通过 (20.6.11) 计算下一个近似解。
• 通过 (20.6.4) 在细网格上计算新的缺陷。

$${\tilde{u}}_h^{\mathrm{new}}={\tilde{u}}_h+{\tilde{v}}_h$$

因此，上述粗网格校正方案的一步包括：

• 通过 (20.6.10) 将校正量插值回细网格。

粗网格校正

让我们对比松弛法与粗网格校正方案各自的优缺点。考虑将误差 $v_h$ 展开为离散傅里叶级数。我们将频率谱下半部分的分量称为光滑分量，高频分量称为非光滑分量。我们已经看到，当 $h\to 0$（即网格点数量很大）时，松弛法的收敛速度变得非常缓慢。其原因在于：每次迭代中，光滑分量的振幅仅略微减小。然而，许多松弛方法在每次迭代中能大幅减小非光滑分量的振幅：它们是良好的光滑算子。

另一方面，对于两重网格迭代，波长 $\lesssim 2H$ 的误差分量甚至无法在粗网格上表示，因此无法在该网格上将其完全消除。但恰恰是这些高频分量，可以通过在细网格上进行松弛来有效减小！这促使我们将松弛与粗网格校正的思想结合起来：

两重网格迭代

• 预光滑（Pre-smoothing）：对 ${\tilde{u}}_h$ 应用 ${\nu }_1\ge 0$ 步松弛方法，得到 ${\bar{u}}_h$。
• 粗网格校正（Coarse-grid correction）：如上所述，利用 ${\overline{u}}_h$ 得到 ${\overline{u}}_h^{\mathrm{new}}$。
• 后光滑（Post-smoothing）：对 ${\overline{u}}_h^{\mathrm{new}}$ 应用 ${\nu }_2\ge 0$ 步松弛方法，得到 ${\tilde{u}}_h^{\mathrm{new}}$。

从上述两重网格方法到多重网格方法只有一步之遥。我们不必精确求解粗网格缺陷方程 (20.6.8)，而是可以引入更粗的网格，并使用两重网格迭代方法来获得其近似解。如果两重网格方法的收敛因子足够小，我们只需进行少量迭代即可获得足够好的近似解。我们将此类迭代的次数记为 $\gamma$。显然，我们可以递归地将这一思想应用到最粗的网格。在最粗网格上，解很容易获得，例如通过直接矩阵求逆，或通过松弛方案迭代至收敛。

从最细网格出发，逐层到更粗网格再返回最细网格的一次多重网格迭代称为一个循环（cycle）。循环的具体结构取决于 $\gamma$（即每个中间阶段进行的两重网格迭代次数）。当 $\gamma =1$ 时称为 V 循环，$\gamma =2$ 时称为 W 循环（见图 20.6.1）。这两种情形在实际应用中最为重要。

注意，一旦涉及两个以上的网格，在最细网格上第一次之后的预光滑步骤需要一个误差 $v$ 的初始近似。该初始近似应取为零。

20.6.2 平滑、限制与延拓算子

最流行的平滑方法（也是你应该首先尝试的方法）是 Gauss-Seidel 方法，因为它通常能带来良好的收敛速度。如果我们把网格点从 0 到 $N-1$ 编号，则 Gauss-Seidel 格式为：

$$u_i=-(\sum _{\begin{array}{c}j=0\\ j\ne i\end{array}}^{N-1}{L}_{ij}{u}_j-f_i)\frac{1}{L_{ii}}i=0,\dots ,N-1$$

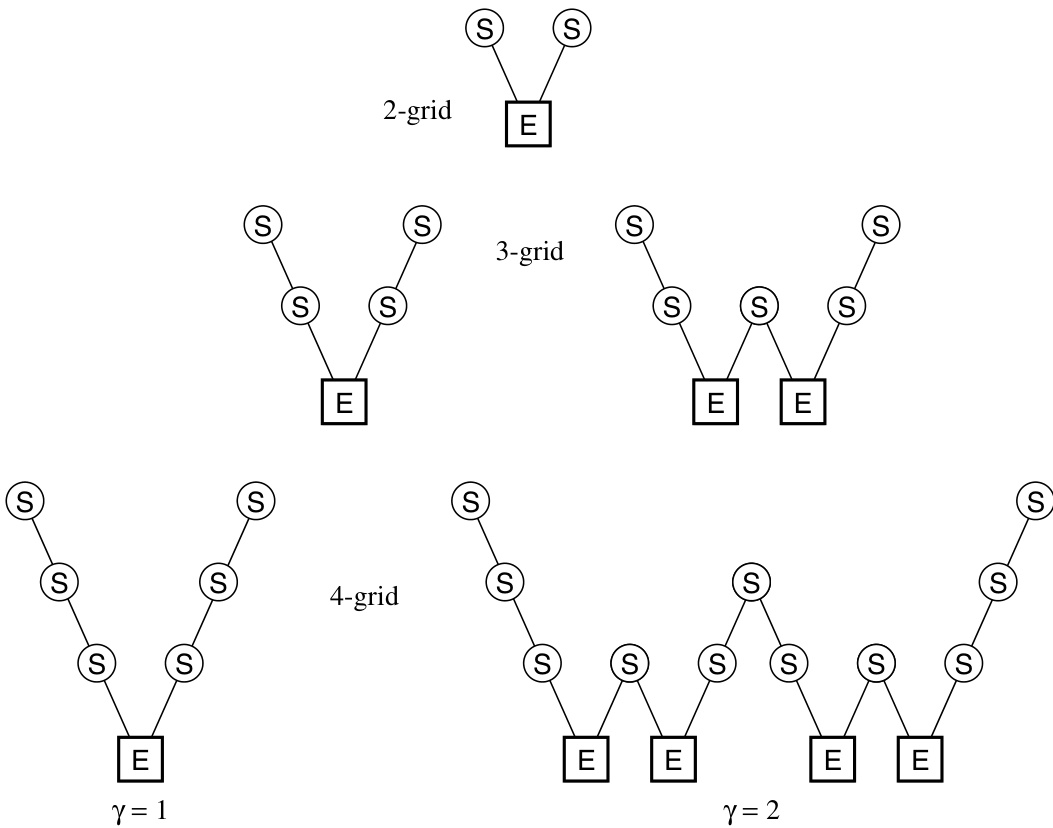
图 20.6.1 多重网格循环的结构。S 表示平滑，E 表示在最粗网格上的精确求解。每条下降线 $</span>$

其中，一旦 $u$ 的新值可用，就立即在右侧使用。Gauss-Seidel 方法的具体形式取决于所选的网格点排序方式。对于典型的二阶椭圆方程（例如我们的模型问题方程 (20.0.3)，其差分形式见方程 (20.0.8)），通常最好采用红黑排序：先遍历网格更新“偶数”点（类似于棋盘上的红格），再遍历更新“奇数”点（黑格）。当某一维度上的耦合比其他维度更强时，应同时松弛该维度上的一整条线。对于最近邻耦合，线松弛涉及求解一个三对角系统，因此仍然高效。在连续两次遍历中分别松弛奇数行和偶数行的方法称为斑马松弛（zebra relaxation），通常优于简单的线松弛。

注意：不应将 SOR 用作平滑算子。超松弛会破坏高频分量的平滑效果，而这对于多重网格方法至关重要。

延拓和限制算子的一种简洁表示方法是给出它们的“符号”（symbol）。$\mathcal{P}$ 的符号可通过如下方式得到：假设 $v_H$ 在某个网格点 $(x,y)$ 处为 1，其余位置为 0，然后考察 $\mathcal{P}{v}_H$ 的值。最常用的延拓算子是简单的双线性插值。它在九个点 $(x,y)$、$(x+h,y)$、$\dots$、$(x-h,y-h)$ 上给出非零值，对应的值分别为 1、$\frac{1}{2}$、$\dots$、$\frac{1}{4}$。

因此其符号为：

$$\left[\begin{array}{lll}\frac{1}{4}& \frac{1}{2}& \frac{1}{4}\\ \frac{1}{2}& 1& \frac{1}{2}\\ \frac{1}{4}& \frac{1}{2}& \frac{1}{4}\end{array}\right]$$

$\mathcal{R}$ 的符号定义如下：假设 $v_h$ 在细网格上处处有定义，然后考察 $\mathcal{R}{v}_h$ 在 $(x,y)$ 处的值如何表示为这些值的线性组合。$\mathcal{R}$ 最简单的选择是直接注入（straight injection），即直接将细网格上对应点的值赋给粗网格点。其符号为 "[1]"。然而，实践中这种选择可能会带来困难。事实证明，一个稳妥的选择是令 $\mathcal{R}$ 为 $\mathcal{P}$ 的伴随算子（adjoint operator）。为定义伴随算子，先定义网格步长为 $h$ 时两个网格函数 $u_h$ 和 $v_h$ 的内积为：

$$⟨u_h|v_h{⟩}_h\equiv h^2\sum _{x,y}{u}_h(x,y)v_h(x,y)$$

则 $\mathcal{P}$ 的伴随算子 ${\mathcal{P}}^{†}$ 由下式定义：

$$⟨u_H|{\mathcal{P}}^{†}{v}_h{⟩}_H=⟨\mathcal{P}{u}_H|v_h{⟩}_h$$

现在令 $\mathcal{P}$ 为双线性插值，并取 $u_H=1$ 在 $(x,y)$ 处，其余为 0。在 (20.6.15) 中令 ${\mathcal{P}}^{†}=\mathcal{R}$ 且 $H=2h$。你会发现：

$$(\mathcal{R}{v}_h{)}_{(x,y)}=\frac{1}{4}{v}_h(x,y)+\frac{1}{8}{v}_h(x+h,y)+\frac{1}{16}{v}_h(x+h,y+h)+\cdots$$

因此 $\mathcal{R}$ 的符号为：

$$\begin{array}{r}\left[\begin{array}{lll}\frac{1}{16}& \frac{1}{8}& \frac{1}{16}\\ \frac{1}{8}& \frac{1}{4}& \frac{1}{8}\\ \frac{1}{16}& \frac{1}{8}& \frac{1}{16}\end{array}\right]\end{array}$$

注意一个简单规则：$\mathcal{R}$ 的符号等于 $\mathcal{P}$ 符号矩阵的转置乘以 $\frac{1}{4}$（见方程 (20.6.13)）。只要 $\mathcal{R}={\mathcal{P}}^{†}$ 且 $H=2h$，这一规则普遍成立。

(20.6.17) 中给出的 $\mathcal{R}$ 的具体选择称为全加权（full weighting）。另一种流行的 $\mathcal{R}$ 选择是半加权（half weighting），介于全加权和直接注入之间。其符号为：

$$\left[\begin{array}{lll}0& \frac{1}{8}& 0\\ \frac{1}{8}& \frac{1}{2}& \frac{1}{8}\\ 0& \frac{1}{8}& 0\end{array}\right]$$

类似的符号也可用于描述差分算子 ${\mathcal{L}}_h$。例如，模型问题的标准差分格式（方程 (20.0.6)）可用五点差分星形表示为：

$${\mathcal{L}}_h=\frac{1}{h^2}\left[\begin{array}{lll}0& 1& 0\\ 1& -4& 1\\ 0& 1& 0\end{array}\right]$$

如果你面对一个新问题，不确定应如何选择 $\mathcal{P}$ 和 $\mathcal{R}$ 才能取得良好效果，这里有一条稳妥的准则：设 $m_p$ 是插值算子 $\mathcal{P}$ 的阶数（即它能精确插值次数为 $m_p-1$ 的多项式），设 $m_r$ 是 $\mathcal{R}$ 的阶数，且 $\mathcal{R}$ 是某个 $\mathcal{P}$ 的伴随算子（不一定是你打算使用的那个 $\mathcal{P}$）。若微分算子 ${\mathcal{L}}_h$ 的阶数为 $m$，则应满足不等式 $m_p+m_r>m$。例如，对于泊松方程，双线性插值及其伴随算子（全加权）满足 $m_p+m_r=4>m=2$。

当然，$\mathcal{P}$ 和 $\mathcal{R}$ 算子应满足你问题的边界条件。最简单的方法是通过必要时修改源项，将差分方程改写为齐次边界条件形式（参见 §20.4）。满足齐次边界条件只需 $\mathcal{P}$ 算子在相应的边界点上产生零值。对应的 $\mathcal{R}$ 算子则通过 $\mathcal{R}={\mathcal{P}}^{†}$ 得到。

20.6.3 完全多重网格算法

到目前为止，我们将多重网格描述为一种迭代方案：从最细网格上的某个初始猜测出发，执行足够多的循环（V 循环、W 循环等）以达到收敛。这是使用多重网格最简单的方式：只需执行足够多的循环，直到满足某个适当的收敛准则。然而，通过使用完全多重网格算法（Full Multigrid, FMG），也称为嵌套迭代（nested iteration），可以进一步提高效率。

FMG 不是从最细网格上的任意近似（例如 $u_h=0$）开始，而是通过从粗网格解插值得到第一个近似：

$$u_h=\mathcal{P}{u}_H$$

而粗网格解本身也是通过类似的 FMG 过程从更粗的网格得到的。在最粗的层次上，直接从精确解开始。因此，FMG 并非如图 20.6.1 所示那样进行，而是通过一系列越来越高的“N”形路径逐步逼近解，每个更高的“N”探测更细的网格（见图 20.6.2）。

注意，(20.6.20) 中的 $\mathcal{P}$ 不必与多重网格循环中使用的 $\mathcal{P}$ 相同。它至少应与离散化算子 ${\mathcal{L}}_h$ 具有相同的阶数，但有时使用更高阶的算子反而能带来更高的效率。

事实证明，通常在每一层上只需执行一次，最多两次多重网格循环，即可继续向下一层更细的网格推进。虽然理论上有关于所需循环次数的指导（例如 [3]），但你可以很容易地通过实验确定它。固定最细的网格层级，研究当你增加每层的循环次数时解的变化情况。解的渐近值即为差分方程的精确解。该精确解与少量循环次数所得解之间的差异即为迭代误差。接下来，固定循环次数为一个较大的值，并改变网格层数（即所用的最小 $h$ 值）。通过这种方式，你可以估计给定 $h$ 下的截断误差。在最终的生产代码中，没有必要使用超过将迭代误差降至截断误差量级所需的循环次数。

简单的多重网格迭代（循环）仅在最细网格上需要右端项 $f$。而全多重网格法（FMG）则需要在所有层级上都提供 $f$。如果边界条件是齐次的，你可以使用 $f_H=\mathcal{R}{f}_h$。但对于非齐次边界条件，这种做法并不总是安全的。在这种情况下，最好在每个粗网格上直接对 $f$ 进行离散化。

注意，FMG 算法会在所有层级上生成解。因此，它可以与诸如 Richardson 外推等技术结合使用。

图 20.6.2. 全多重网格（FMG）方法的循环结构（符号说明见图 20.6.1）。该方法从最粗网格开始，进行插值，然后通过“V”型循环逐步将解细化到越来越细的网格上。

我们现在给出一个名为 Mglin 的例程，用于实现线性方程的全多重网格算法，即模型问题 (20.0.6)。该例程使用红黑 Gauss-Seidel 作为光滑算子，双线性插值作为 $\mathcal{P}$，半权平均作为 $\mathcal{R}$。若要修改该例程以处理其他线性问题，只需适当修改 relax、resid 和 slvsml 函数即可。该例程的一个特点是动态分配各个网格上变量所需的存储空间。

用于求解线性椭圆型方程的全多重网格算法，此处针对单位正方形区域上的模型问题 (20.0.6)，因此 $\Delta =1/(\mathrm{n}-1)$。

输入时，u[0..n-1][0..n-1] 包含右端项 $\rho$，输出时返回解。维度 n 必须形如 $2^j+1$，其中 $j$ 为某整数。（实际上 $j$ 即为解中所用的网格层数，下文称为 ng。）ncycle 表示每层所用的 V 循环次数。

Int nn = n;
while (nn >= 1) ng++;
if ((n - 1) != (1 << ng))
    throw("n-1 must be a power of 2 in mglin.");
nn = n;
Int ngrid = ng - 1;
rho resized(ng);
rho[ngrid] = new MatDoub(nn, nn);
*rho[ngrid] = u;
while (nn > 3) {
    nn = nn / 2 + 1;
    rho[--ngrid] = new MatDoub(nn, nn);
    rstrict(*rho[ngrid], *rho[ngrid + 1]);
}

n = 3;
uj = new MatDoub(nn, nn);
slvsml(*uj, *rho[0]);
for (Int j = 1; j < ng; j++) {
    nn = 2 * nn - 1;
    uj1 = uj;
    uj = new MatDoub(nn, nn);
    interp(*uj, *uj1);
    delete uj1;
    for (Int jcycle = 0; jcycle < ncycle; jcycle++) // V-cycle loop.
        mg(j, *uj, *rho[j]);
}
u = *uj;

~Mglin()
// 析构函数释放存储空间。
{
    if (uj != NULL) delete uj;
    for (Int j = 0; j < ng; j++)
        if (rho[j] != NULL) delete rho[j];
}

通过双线性插值实现从粗网格到细网格的延拓。若 nf 为细网格维度，则粗网格解作为输入 uc[0..nc-1][0..nc-1]，其中 nc = nf/2 + 1。细网格解返回在 uf[0..nf-1][0..nf-1] 中。

Int nf = uf.nrows();
Int nc = nf / 2 + 1;
for (Int jc = 0; jc < nc; jc++) // 处理直接复制的点。
    for (Int ic = 0; ic < nc; ic++)
        uf[2 * ic][2 * jc] = uc[ic][jc];
for (Int jf = 0; jf < nf; jf += 2) // 处理偶数列，垂直方向插值。
    for (Int iif = 1; iif < nf - 1; iif += 2)
        uf[iif][jf] = 0.5 * (uf[iif + 1][jf] + uf[iif - 1][jf]);
for (Int jf = 1; jf < nf - 1; jf += 2) // 处理奇数列，水平方向插值。
    for (Int iif = 0; iif < nf; iif += 2)
        uf[iif][jf] = 0.5 * (uf[iif][jf + 1] + uf[iif][jf - 1]);

void addint(MatDoub_0 &uf, MatDoub_I &uc, MatDoub_0 &res)
// 执行从粗网格到细网格的插值，并将结果加到 uf 上。
// 若 nf 为细网格维度，则粗网格解输入为 uc[0..nc-1][0..nc-1]，其中 nc = nf/2 + 1。
// 细网格解返回在 uf[0..nf-1][0..nf-1] 中。
// res[0..nf-1][0..nf-1] 用作临时存储。
{
    Int nf = uf.nrows();
    interp(res, uc);
    for (Int j = 0; j < nf; j++)
        for (Int i = 0; i < nf; i++)
            uf[i][j] += res[i][j];
}

在最粗网格上求解模型问题，其中 $h=\frac{1}{2}$。右端项输入为 rhs[0..2][0..2]，解返回在 u[0..2][0..2] 中。

Doub h = 0.5;
for (Int i = 0; i < 3; i++)
    for (Int j = 0; j < 3; j++)
        u[i][j] = 0.0;

u[1][1] = -h * h * rhs[1][1] / 4.0;

void relax(MatDoub_IO &u, MatDoub_I &rhs)
// 模型问题的红黑 Gauss-Seidel 松弛。
// 使用右端项函数 rhs[0..n-1][0..n-1] 更新当前解 u[0..n-1][0..n-1]。
{
    Int n = u.nrows();
    Doub h = 1.0 / (n - 1);
    Doub h2 = h * h;
    for (Int ipass = 0, jsw = 1; ipass < 2; ipass++, jsw = 3 - jsw) {
        for (Int j = 1, isw = jsw; j < n - 1; j++, isw = 3 - isw)
            for (Int i = isw; i < n - 1; i += 2)
                u[i][j] = 0.25 * (u[i + 1][j] + u[i - 1][j] + u[i][j + 1]
                                 + u[i][j - 1] - h2 * rhs[i][j]);
    }
}

void resid(MatDoub_O &res, MatDoub_I &u, MatDoub_I &rhs)
// 返回模型问题的负残差。
// 输入量为 u[0..n-1][0..n-1] 和 rhs[0..n-1][0..n-1]，
// 返回 res[0..n-1][0..n-1]。
{
    Int n = u.nrows();
    Doub h = 1.0 / (n - 1);
    Doub h2i = 1.0 / (h * h);
    for (Int j = 1; j < n - 1; j++)
        for (Int i = 1; i < n - 1; i++)
            res[i][j] = -h2i * (u[i + 1][j] + u[i - 1][j] + u[i][j + 1]
                               + u[i][j - 1] - 4.0 * u[i][j] + rhs[i][j]);
    for (Int i = 0; i < n; i++) // 边界点。
        res[i][0] = res[i][n - 1] = res[0][i] = res[n - 1][i] = 0.0;
}

void rstrict(MatDoub_O &uc, MatDoub_I &uf)
// 半权平均限制算子。
// 若 nc 为粗网格维度，则细网格解输入为 uf[0..2*nc-2][0..2*nc-2]。
// 通过限制得到的粗网格解返回在 uc[0..nc-1][0..nc-1] 中。
{
    Int nc = uc.nrows();
    Int ncc = 2 * nc - 2;
    for (Int jf = 2, jc = 1; jc < nc - 1; jc++, jf += 2) {
        for (Int iif = 2, ic = 1; ic < nc - 1; ic++, iif += 2) {
            uc[ic][jc] = 0.5 * uf[iif][jf] + 0.125 * (uf[iif + 1][jf] + uf[iif - 1][jf]
                                                    + uf[iif][jf + 1] + uf[iif][jf - 1]);
        }
    }
    for (Int jc = 0, ic = 0; ic < nc; ic++, jc += 2) {
        uc[ic][0] = uf[jc][0];
        uc[ic][nc - 1] = uf[jc][ncc];
    }
    for (Int jc = 0, ic = 0; ic < nc; ic++, jc += 2) {
        uc[0][ic] = uf[0][jc];
        uc[nc - 1][ic] = uf[ncc][jc];
    }
}

void mg(Int j, MatDoub_IO &u, MatDoub_I &rhs)
// 递归多重网格迭代。
// 输入：j 为当前层级，u 为当前解，rhs 为右端项。
// 输出：u 包含当前层级的改进解。
// 在计算粗网格校正前后进行的松弛 sweeps 次数。
{
    if (j == 0)
        slvsml(u, rhs);
    else {
        Int nc = (u.nrows() + 1) / 2;
        Int nf = u.nrows();
        MatDoub res(nc, nc), v(nc, nc, 0.0), temp(nf, nf);
        // v 初始化为零，作为每次松弛的初始猜测。
        for (Int jpre = 0; jpre < NPRE; jpre++)
            relax(u, rhs);
        resid(temp, u, rhs);
        rstrict(res, temp);
        mg(j - 1, v, res);
        addint(u, v, temp);
        for (Int jpost = 0; jpost < NPOST; jpost++)
            relax(u, rhs);
    }
}

例程 Mglin 的编写以清晰性而非最高效率为目标，因此易于修改。以下几项简单改动可加快执行速度：

• 在红黑 Gauss-Seidel 步骤之后，缺陷 $d_h$ 在所有黑点上恒为零。因此，对于半权平均限制算子，$d_H=R{d}_h$ 简化为仅将细网格上一半的缺陷直接复制到对应的粗网格点上。V 循环前半部分中对 resid 和 rstrict 的调用可替换为一个仅遍历粗网格的例程，直接用一半的缺陷填充粗网格。

• 类似地，量 ${\tilde{u}}_h^{\mathrm{new}}={\tilde{u}}_h+\mathcal{P}{\tilde{v}}_H$ 无需在红点上计算，因为它们会在随后的 Gauss-Seidel sweep 中立即被重新定义。这意味着 addint 只需遍历黑点即可。

• 你可以通过几种方式加速 relax：首先，当初始猜测为零时，可采用特殊形式；其次，可在各网格上预先存储 $h^2{f}_h$ 以节省一次乘法；最后，通过引入中间变量重写 Gauss-Seidel 公式，可节省一次加法运算。

• 对于典型问题，当 ncycle = 1 时，Mglin 返回的解其迭代误差会大于给定网格步长 $h$ 下的截断误差。为了将误差降低到截断误差的量级，必须将 ncycle 设为 2，或者更经济地将 NPRE 设为 2。更高效的方法是，在公式 (20.6.20) 中使用比 V-cycle 中线性插值更高阶的 $\mathcal{P}$。

实现上述所有特性通常可使执行时间提升最多两倍，在生产代码中显然是值得的。

20.6.4 非线性多重网格：FAS 算法

现在转向求解非线性椭圆型方程，我们将其形式化地写作：

$$\mathcal{L}(u)=0$$

任何显式的源项都已移到等式左侧。假设方程 (20.6.21) 已被适当离散化：

$${\mathcal{L}}_h(u_h)=0$$

我们将在下文看到，在多重网格算法中，我们需要处理那些在求解过程中产生非零右端项的方程：

$${\mathcal{L}}_h(u_h)=f_h$$

一种利用多重网格求解非线性问题的方法是使用牛顿法，该方法在每次迭代中生成关于修正项的线性方程，然后我们可以用线性多重网格法求解这些方程。然而，多重网格思想的一大优势在于它可以直接应用于非线性问题。我们只需要一种合适的非线性松弛方法来平滑误差，再加上一种在粗网格上近似修正量的程序。这种直接方法就是 Brandt 提出的全近似存储算法（Full Approximation Storage, FAS）。除了可能在最粗网格上外，无需显式求解任何非线性方程。

为推导非线性算法，假设我们有一种松弛过程，能够像在线性情形中那样平滑残差向量。那么我们可以寻找一个平滑的修正量 $v_h$ 来求解 (20.6.23)：

$${\mathcal{L}}_h({\tilde{u}}_h+v_h)=f_h$$

为求 $v_h$，注意到：

$$\begin{array}{r}{\mathcal{L}}_h({\tilde{u}}_h+v_h)-{\mathcal{L}}_h({\tilde{u}}_h)=f_h-{\mathcal{L}}_h({\tilde{u}}_h)\\ =-d_h\end{array}$$

在经过若干次非线性松弛迭代后，右端项是平滑的。因此我们可以将左端项转移到粗网格上：

$${\mathcal{L}}_H(u_H)-{\mathcal{L}}_H(\mathcal{R}{\tilde{u}}_h)=-\mathcal{R}{d}_h$$

即，我们在粗网格上求解：

$${\mathcal{L}}_H(u_H)={\mathcal{L}}_H(\mathcal{R}{\tilde{u}}_h)-\mathcal{R}{d}_h$$

（这正是非零右端项出现的方式。）假设近似解为 ${\tilde{u}}_H$，则粗网格修正量为：

$$v_H=u_H-\mathcal{R}{\tilde{u}}_h$$

从而得到更新后的细网格解：

$${\tilde{u}}_h^{\mathrm{new}}={\tilde{u}}_h+\mathcal{P}({\tilde{u}}_H-\mathcal{R}{\tilde{u}}_h)$$

注意，一般情况下 $\mathcal{PR}\ne 1$，因此 ${\tilde{u}}_h^{\mathrm{new}}\ne \mathcal{P}{\tilde{u}}_H$。这是一个关键点：在公式 (20.6.29) 中，插值误差仅来自修正量，而非完整的解 ${\tilde{u}}_H$。

公式 (20.6.27) 表明，我们求解的是完整的近似解 $u_H$，而不仅仅是像在线性算法中那样求解误差。这正是“全近似存储”（FAS）这一名称的由来。

因此，FAS 多重网格算法看起来与线性多重网格算法非常相似。唯一的区别在于，缺陷 $d_h$ 和松弛后的近似解 $u_h$ 都必须限制到粗网格上，而在粗网格上通过递归调用算法求解的是方程 (20.6.27)。然而，我们并不直接按此方式实现该算法，而是首先介绍所谓的“对偶观点”（dual viewpoint），它提供了一种看待多重网格思想的强有力替代视角。

对偶观点考虑局部截断误差，其定义为：

$$\tau \equiv {\mathcal{L}}_h(u)-f_h$$

其中 $u$ 是原始连续方程的精确解。若将其改写为：

$${\mathcal{L}}_h(u)=f_h+\tau$$

我们便可以看出，$\tau$ 可被视为对 $f_h$ 的修正，使得细网格方程的解恰好是精确解 $u$。

现在考虑相对截断误差 ${\tau }_h$，它是在 $H$-网格上相对于 $h$-网格定义的：

$${\tau }_h\equiv {\mathcal{L}}_H(\mathcal{R}{u}_h)-\mathcal{R}{\mathcal{L}}_h(u_h)$$

由于 ${\mathcal{L}}_h(u_h)=f_h$，上式可重写为

$${\mathcal{L}}_H(u_H)=f_H+{\tau }_h$$

换句话说，我们可以将 ${\tau }_h$ 视为对 $f_H$ 的修正项，使得粗网格方程的解等于细网格的解。当然，我们无法直接计算 ${\tau }_h$，但可以通过在方程 (20.6.32) 中使用 ${\tilde{u}}_h$ 得到其近似值：

$${\tau }_h\simeq {\tilde{\tau }}_h\equiv {\mathcal{L}}_H(\mathcal{R}{\tilde{u}}_h)-\mathcal{R}{\mathcal{L}}_h({\tilde{u}}_h)$$

将方程 (20.6.33) 中的 ${\tau }_h$ 替换为 ${\tilde{\tau }}_h$，得到

$${\mathcal{L}}_H(u_H)={\mathcal{L}}_H(\mathcal{R}{\tilde{u}}_h)-\mathcal{R}{d}_h$$

这正是粗网格方程 (20.6.27)！

因此，我们看到粗网格与细网格之间关系存在两种互补的观点：

• 粗网格用于加速细网格残差中光滑分量的收敛；
• 细网格用于计算对粗网格方程的修正项，从而在粗网格上获得细网格精度。

这种新观点的一个好处是，它使我们能够导出多重网格迭代的一种自然停止准则。通常该准则为

$$\Vert d_h\Vert \le ϵ$$

问题是如何选择 $ϵ$。显然，当剩余误差主要由局部截断误差 $\tau$ 主导时，继续迭代已无益处。可计算的量是 ${\tilde{\tau }}_h$。那么 $\tau$ 与 ${\tilde{\tau }}_h$ 之间有何关系？对于典型的二阶精度差分格式，

$$\tau ={\mathcal{L}}_h(u)-{\mathcal{L}}_h(u_h)=h^2{\tau }_2(x,y)+\cdots$$

假设解满足 $u_h=u+h^2{u}_2(x,y)+\cdots$。再假设限制算子 $\mathcal{R}$ 的精度足够高，其影响可忽略，则方程 (20.6.32) 给出

$$\begin{array}{rl}& {\tau }_h\simeq {\mathcal{L}}_H(u+h^2{u}_2)-{\mathcal{L}}_h(u+h^2{u}_2)\\ & ={\mathcal{L}}_H(u)-{\mathcal{L}}_h(u)+h^2[{\mathcal{L}}_H^{\prime }(u_2)-{\mathcal{L}}_h^{\prime }(u_2)]+\cdots \\ & =(H^2-h^2){\tau }_2+O(h^4)\end{array}$$

对于通常情形 $H=2h$，因此有

$$\tau \simeq \frac{1}{3}{\tau }_h\simeq \frac{1}{3}{\tilde{\tau }}_h$$

因此，停止准则即为方程 (20.6.36)，其中

$$ϵ=\alpha \Vert {\tilde{\tau }}_h\Vert ,\alpha \sim \frac{1}{\mathfrak{R}}$$

在实现非线性多重网格算法之前，我们还有一项任务：选择一种非线性松弛格式。通常，你的首选应是非线性高斯-赛德尔（Gauss-Seidel）格式。若将离散化方程 (20.6.23) 按某种排序写为

$$L_i(u_0,\dots ,u_{N-1})=f_i,i=0,\dots ,N-1$$

则非线性高斯-赛德尔格式通过求解

$$L_i(u_0,\dots ,u_{i-1},u_i^{\mathrm{new}},u_{i+1},\dots ,u_{N-1})=f_i$$

来更新 $u_i^{\mathrm{new}}$。与通常做法一样，一旦计算出新的 $u$ 值，就立即替换旧值。通常方程 (20.6.42) 对 $u_i^{\mathrm{new}}$ 是线性的，因为非线性项是通过其邻点离散化的。若非如此，我们则用一步牛顿迭代代替方程 (20.6.42)：

$$u_i^{\mathrm{new}}=u_i^{\mathrm{old}}-\frac{L_i(u_i^{\mathrm{old}})-f_i}{\partial L_i(u_i^{\mathrm{old}})/\partial u_i}$$

例如，考虑如下简单非线性方程

$${\nabla }^{2}u+u^2=\rho$$

在二维记号下，我们有

$$\mathcal{L}(u_{i,j})=(u_{i+1,j}+u_{i-1,j}+u_{i,j+1}+u_{i,j-1}-4u_{i,j})/h^2+u_{i,j}^2-{\rho }_{i,j}=0(\mathrm{20.6.45})$$

由于

$$\frac{\partial \mathcal{L}}{\partial u_{i,j}}=-4/h^2+2u_{i,j}$$

牛顿-高斯-赛德尔迭代格式为

$$u_{i,j}^{\mathrm{new}}=u_{i,j}-\frac{\mathcal{L}(u_{i,j})}{-4/h^2+2u_{i,j}}$$

下面是一个名为 Mgfas 的例程，它使用完全多重网格（full multigrid）算法和 FAS（Full Approximation Scheme）方案求解方程 (20.6.44)。限制（restriction）和延拓（prolongation）操作与 Mglin 中相同。我们加入了基于方程 (20.6.40) 的收敛性检验。一个成功的多重网格求解应力求在最大 V-循环次数 maxcyc 等于 1 或 2 的情况下满足该条件。例程 Mgfas 使用与 Mglin 相同的 interp 和 rstrct 函数。

用于 FAS 求解非线性椭圆型方程的完全多重网格算法，此处针对单位正方形区域上的方程 (20.6.44)，因此 $h=1/(\mathbf{n}-1)$。

Mgfas(MatDoub_IO &u, const Int maxcyc) : n(u.nrows()), ng(0)

输入时，u[0..n-1][0..n-1] 包含右端项 $\rho$，输出时返回解。维数 n 必须具有形式 $2^j+1$，其中 $j$ 为某整数。（实际上，$j$ 即为求解中所用的网格层数，下文称为 ng。）maxcyc 是每层所允许的最大 V-循环次数。

Int nn = n;
while (nn >= 1) ng++;
if ((n - 1) != (1 << ng))
    throw("n-1 must be a power of 2 in mgfas.");
nn = n;
Int ngrid = ng - 1;
rho.resize(ng);
rho[ngrid] = new MatDoub(nn, nn);
*rho[ngrid] = u;
while (nn > 3) {
    nn = nn / 2 + 1;
    rho[--ngrid] = new MatDoub(nn, nn);
    rstrct(*rho[ngrid], *rho[ngrid + 1]);
}
nn = 3;
uj = new MatDoub(nn, nn);
slvsm2(*uj, *rho[0]);  // 最粗网格上的初始解
for (Int j = 1; j < ng; j++) {
    nn = 2 * nn - 1;
    uj1 = uj;
    uj = new MatDoub(nn, nn);
    // 嵌套迭代循环
    // 从第 j-1 层网格插值到下一层更细的网格 j
    interp(*uj1, *uj);
}
MatDoub temp(nn, nn);
for (Int jcycle = 0; jcycle < maxcyc; jcycle++) {  // V-循环循环
    // 右端项为哑变量
    Mg(j, *uj, temp, rho, trerr);
    lop(temp, *uj);
    Doub res = anorm2(temp);
    if (res < trerr) break;
}
u = *uj;

~Mgfas()

析构函数释放存储空间。

{
    if (uj != NULL) delete uj;
    for (Int j = 0; j < ng; j++)
        if (rho[j] != NULL) delete rho[j];
}

void matadd(MatDoub_I &a, MatDoub_I &b, MatDoub_O &c)
// 矩阵加法：将 a[0..n-1][0..n-1] 与 b[0..n-1][0..n-1] 相加，结果存入 c[0..n-1][0..n-1]。
{
    Int n = a.nrows();
    for (Int j = 0; j < n; j++)
        for (Int i = 0; i < n; i++)
            c[i][j] = a[i][j] + b[i][j];
}

void matsub(MatDoub_I &a, MatDoub_I &b, MatDoub_O &c)
// 矩阵减法：从 a[0..n-1][0..n-1] 中减去 b[0..n-1][0..n-1]，结果存入 c[0..n-1][0..n-1]。
{
    Int n = a.nrows();
    for (Int j = 0; j < n; j++)
        for (Int i = 0; i < n; i++)
            c[i][j] = a[i][j] - b[i][j];
}

void slvsm2(MatDoub_O &u, MatDoub_I &rhs)
// 在最粗网格上求解方程 (20.6.44)，其中 $h = \frac{1}{2}$。
// 右端项输入在 rhs[0..2][0..2] 中，解返回在 u[0..2][0..2] 中。
{
    Doub h = 0.5;
    for (Int i = 0; i < 3; i++)
        for (Int j = 0; j < 3; j++)
            u[i][j] = 0.0;
    Doub fact = 2.0 / (h * h);
    Doub disc = sqrt(fact * fact + rhs[1][1]);
    u[1][1] = -rhs[1][1] / (fact + disc);
}

void relax2(MatDoub_IO &u, MatDoub_I &rhs)
// 对方程 (20.6.44) 进行红黑 Gauss-Seidel 松弛。
// 使用右端项函数 rhs[0..n-1][0..n-1] 更新当前解 u[0..n-1][0..n-1]。
{
    Int n = u.nrows();
    Int jsw = 1;
    Doub h = 1.0 / (n - 1);
    Doub h2i = 1.0 / (h * h);
    Doub foh2 = -4.0 * h2i;
    for (Int ipass = 0; ipass < 2; ipass++, jsw = 3 - jsw) {
        Int isw = jsw;
        for (Int j = 1; j < n - 1; j++, isw = 3 - isw) {
            for (Int i = isw; i < n - 1; i += 2) {
                Doub res = h2i * (u[i+1][j] + u[i-1][j] + u[i][j+1] + u[i][j-1] - 4.0 * u[i][j]) + u[i][j] * u[i][j] - rhs[i][j];
                u[i][j] = u[i][j] - res / (foh2 + 2.0 * u[i][j]); // Newton-Gauss-Seidel 公式
            }
        }
    }
}

void rstrict(MatDoub_O &uc, MatDoub_I &uf)
// 半权限制算子。
// 若 nc 为粗网格维数，则细网格解输入在 uf[0..2*nc-2][0..2*nc-2] 中。
// 通过限制得到的粗网格解返回在 uc[0..nc-1][0..nc-1] 中。
{
    Int nc = uc.nrows();
    Int ncc = 2 * nc - 2;
    // 内部点
    for (Int jc = 1, jf = 2; jc < nc - 1; jc++, jf += 2) {
        for (Int ic = 1, if_ = 2; ic < nc - 1; ic++, if_ += 2) {
            uc[ic][jc] = 0.5 * uf[if_][jf] + 0.125 * (uf[if_+1][jf] + uf[if_-1][jf] + uf[if_][jf+1] + uf[if_][jf-1]);
        }
    }
    // 边界点
    for (Int ic = 0, jc = 0; ic < nc; ic++, jc += 2) {
        uc[ic][0] = uf[jc][0];
        uc[ic][nc-1] = uf[jc][ncc];
    }
    for (Int ic = 0, jc = 0; ic < nc; ic++, jc += 2) {
        uc[0][ic] = uf[0][jc];
        uc[nc-1][ic] = uf[ncc][jc];
    }
}

void lop(MatDoub_0 &out, MatDoub_I &u)
// 给定 u[0..n-1][0..n-1]，在 out[0..n-1][0..n-1] 中返回方程 (20.6.44) 的 $\mathcal{L}_{h}(\widetilde{u}_{h})$。
{
    Int n = u.nrows();
    Doub h = 1.0 / (n - 1);
    Doub h2i = 1.0 / (h * h);
    for (Int i = 1; i < n - 1; i++)
        for (Int j = 1; j < n - 1; j++)
            out[i][j] = h2i * (u[i + 1][j] + u[i - 1][j] + u[i][j + 1] + u[i][j - 1] - 4.0 * u[i][j]) + (u[i][j] * u[i][j]);
    for (Int i = 0; i < n; i++)
        out[i][0] = out[i][n - 1] = out[0][i] = out[n - 1][i] = 0.0;
}

void interp(MatDoub_0 &uf, MatDoub_I &uc)
// 通过双线性插值实现从粗网格到细网格的延拓。若 nf 是细网格维数，则粗网格解作为 uc[0..nc-1][0..nc-1] 输入，其中 nc = nf/2 + 1。
// 细网格解返回在 uf[0..nf-1][0..nf-1] 中。
{
    Int nf = uf.nrows();
    Int nc = nf / 2 + 1;
    // 复制对应点
    for (Int jc = 0; jc < nc; jc++)
        for (Int ic = 0; ic < nc; ic++)
            uf[2 * ic][2 * jc] = uc[ic][jc];
    // 对偶数列进行垂直方向插值
    for (Int jf = 0; jf < nf; jf += 2)
        for (Int if_ = 1; if_ < nf - 1; if_ += 2)
            uf[if_][jf] = 0.5 * (uf[if_ + 1][jf] + uf[if_ - 1][jf]);
    // 对奇数列进行水平方向插值
    for (Int if_ = 0; if_ < nf; if_++)
        for (Int jf = 1; jf < nf - 1; jf += 2)
            uf[if_][jf] = 0.5 * (uf[if_][jf + 1] + uf[if_][jf - 1]);
}

Doub anorm2(MatDoub_I &a)
// 返回矩阵 a[0..n-1][0..n-1] 的欧几里得范数。
{
    Doub sum = 0.0;
    Int n = a.nrows();
    for (Int j = 0; j < n; j++)
        for (Int i = 0; i < n; i++)
            sum += a[i][j] * a[i][j];
    return sqrt(sum) / n;
}

void mg(const Int j, MatDoub_IO &u, MatDoub_I &rhs, NRvector<NRmatrix<Doub> *> &rho, Doub &trerr)
// 递归多重网格迭代。输入时，j 为当前层级，u 为当前解。对于某一层级的首次调用，右端项为零，rhs 为哑变量，
// 此时通过输入 trerr > 0 表示。后续递归调用提供非零 rhs（如方程 (20.6.33) 所示），此时通过输入 trerr < 0 表示。
// rho 是指向各层级 $\rho$ 的指针向量。输出时，u 包含当前层级的改进解。首次调用某一层级时，相对截断误差 $\tau$ 通过 trerr 返回。

const Int NPRE = 1, NPOST = 1;
// 在计算粗网格修正前后进行的松弛迭代次数。

const Doub ALPHA = 0.33;

Doub dum = -1.0;
Int nf = u.nrows();
Int nc = (nf + 1) / 2;
MatDoub temp(nf, nf);

if (j == 0) {
    matadd(rhs, *rho[j], temp);
    slvsm2(u, temp);
} else {
    MatDoub v(nc, nc), ut(nc, nc), tau(nc, nc), tempc(nc, nc);
    for (Int jpre = 0; jpre < NPRE; jpre++) {
        // 预平滑
        if (trerr < 0.0) {
            matadd(rhs, *rho[j], temp);
            relax2(u, temp);
        } else
            relax2(u, *rho[j]);
    }
    rstrict(ut, u);
    v = ut;
    lop(tau, ut);
    lop(temp, u);
    if (trerr < 0.0)
        matsub(temp, rhs, temp);
    rstrict(temp, tempc);
    matsub(tau, tempc, tau);
    if (trerr > 0.0)
        trerr = ALPHA * anorm2(tau);
    mg(j - 1, v, tau, rho, dum);
    matsub(v, ut, tempc);
    interp(temp, tempc);
    matadd(u, temp, u);

    for (Int jpost = 0; jpost < NPOST; jpost++) {
        matadd(rhs, *rho[j], temp);
        relax2(u, temp);
    }
}

参考文献

Brandt, A. 1977, "Multilevel Adaptive Solutions to Boundary-Value Problems," Mathematics of Computation, vol. 31, pp. 333–390.[1]

Brandt, A. 1982, in Multigrid Methods, W. Hackbusch and U. Trottenberg, eds. (Springer Lecture Notes in Mathematics No. 960) (New York: Springer).[2]

Hackbusch, W. 1985, Multi-Grid Methods and Applications (New York: Springer).[3]

Stuben, K., and Trottenberg, U. 1982, in Multigrid Methods, W. Hackbusch and U. Trottenberg, eds. (Springer Lecture Notes in Mathematics No. 960) (New York: Springer), pp. 1–176.[4]

Briggs, W.L., Henson, V.E., and McCormick, S. 2000, A Multigrid Tutorial (Cambridge, UK: Cambridge University Press).[5]

Trottenberg, U., Oosterlee, C.W., and Schuller, A. 2001, Multigrid (Cambridge, MA: Academic Press).[6]

McCormick, S., and Rüde, U., eds. 2006, "Multigrid Computing," special issue of Computing in Science and Engineering, vol. 8, No. 6 (November/December), pp. 10–62.

Hackbusch, W., and Trottenberg, U. (eds.) 1991, Multigrid Methods III (Basel: Birkhäuser).

Wesseling, P. 1992, An Introduction to Multigrid Methods (New York: Wiley); corrected reprint 2004 (Philadelphia: R.T. Edwards).

20.7 谱方法

谱方法是求解偏微分方程（PDE）的一种非常强大的工具。当适用时，如果你需要在多维问题中获得高空间分辨率，谱方法是首选。对于三维问题中的二阶精度有限差分方法，每个维度分辨率提高 2 倍，需要 8 倍的网格点数，通常仅将误差减少 4 倍。而在谱方法中，类似的分辨率提升通常可将误差减少 $10^6$ 倍。即使对于一维问题，谱方法在性能和效率方面也会令你惊叹。

谱方法适用于光滑解。对于激波等不连续问题效果很差——不要尝试使用谱方法。即使是轻微的非光滑性（例如解的某个高阶导数存在不连续）也会破坏谱方法的收敛性。（实际上，如何使谱方法处理不连续和激波是一个活跃的研究领域；参见 [1] 获取入门介绍。）

有限差分方法与谱方法的关键区别在于：有限差分方法近似你试图求解的方程，而谱方法则近似你试图寻找的解。有限差分将连续方程替换为网格点上的离散方程，而谱方法则将解表示为某组基函数的截断展开式。

基函数：

$$f(x)\simeq f_N(x)=\sum _{n=0}^N{a}_n{\varphi }_n(x)$$

基函数的不同选择以及计算系数 $a_n$ 的不同方法，会得到不同类型的谱方法。

20.7.1 示例

我们通过一个例子来说明谱方法的思想。考虑一维单向波动方程（对流方程）：

$$\frac{\partial u}{\partial t}=\frac{\partial u}{\partial x}$$

在区间 $[0,2\pi ]$ 上具有周期性边界条件，初始条件为

$$u(t=0,x)=f(x)$$

通过将 $u$ 展开为傅里叶级数，可得到解析的谱解：

$$u(t,x)=\sum _{n=-\infty }^{\infty }{a}_n(t)e^{inx}$$

将此展开式代入方程 (20.7.2)，得到

$$\frac{d{a}_n}{dt}=in{a}_n$$

其解为

$$a_n(t)=a_n(0)e^{int}$$

系数 $a_n(0)$ 由初始条件确定：将

$$f(x)=\sum _{n=-\infty }^{\infty }{f}_n{e}^{inx}$$

展开，由此可得

$$a_n(0)=f_n$$

例如，假设

$$f(x)=\sin (\pi \cos x)$$

则解析解为

$$u(t,x)=\sin [\pi \cos (x+t)]$$

该解 (20.7.4) 中的谱系数为

$$\begin{array}{rl}& a_n(0)=\frac{1}{2\pi }{\int }_0^{2\pi }\sin (\pi \cos x)e^{-inx}dx\\ & =(-1{)}^{(n-1)/2}{J}_n(\pi ),n\text{ 为奇数}\end{array}$$

在该谱解的数值实现中，我们将展开截断至 $n=N$。那么 $u_N(t,x)$ 对精确解的逼近效果如何？一种度量方式是均方根误差：

$$\begin{array}{rl}& L_2={\left[\frac{1}{2\pi }{\int }_0^{2\pi }|u(t,x)-u_N(t,x){|}^{2}dx\right]}^{1/2}\\ & ={\left[\frac{1}{2\pi }{\int }_0^{2\pi }|{\sum }_{|n|>N}{a}_n(0)e^{inx}{e}^{int}{|}^{2}dx\right]}^{1/2}\\ & ={\left[{\sum }_{|n|>N}|a_n(0){|}^2\right]}^{1/2}\end{array}$$

由于 $J_n(\pi )$ 随 $n\to \infty$ 指数衰减，因此对于任意 $t\ge 0$，误差随 $N$ 呈指数下降。这是优秀谱方法的关键特征，也是我们始终应追求的目标。相比之下，二阶有限差分方法的误差按 $1/N^2$ 的速率衰减。

当解的主要特征被充分解析后，谱方法的这种指数收敛性便开始显现。在上述例子中，一旦 $n\gtrsim \pi$，贝塞尔函数 $J_n(\pi )$ 便迅速趋于零，这相当于每个波长使用约 $\pi$ 个基函数。可以证明，这是谱方法的一个普遍性质 [2]。相比之下，要达到 1% 的精度，二阶有限差分方法每个波长需要约 20 个网格点 [2]。此外，一旦解被充分解析，谱方法的精度提升速度远快于有限差分方法。

函数 $e^{inx}$ 具有以下三个关键性质，使得上述解析谱解（即分离变量法）得以成立：

1. 它们构成一组完备的基函数。

2. 每个基函数本身都满足边界条件。

3. 它们是问题中算子 $d/dx$ 的本征函数。

正如我们将看到的，对于数值谱方法而言，只有性质1是必不可少的。谱方法并不仅限于傅里叶级数——可以使用多种基函数。

20.7.2 基函数的选择

你不能简单地对所有问题都使用傅里叶级数作为基函数——这取决于边界条件。以下方法可以处理你遇到的99%的情况：

• 如果解是周期性的，使用傅里叶级数。
• 如果解是非周期的，且定义域是正方形或立方体，或者可以通过简单的坐标变换映射为矩形区域，则在每个维度上使用切比雪夫多项式。
• 如果定义域是球形的，则在角度方向上使用球谐函数。在径向方向上，对于球壳区域使用切比雪夫多项式；对于包含原点的球体，则使用文献[8]中的径向基函数。这些基函数在原点处具有正确的解析行为，远优于其他选择。它们也可用于柱坐标域。如果定义域是无限的，请参考文献[9,10,4]。

基于切比雪夫或勒让德多项式的展开具有这样的性质：其收敛速率仅由解的光滑性决定，而与其满足的边界条件无关。相比之下，傅里叶展开要实现快速收敛，不仅需要解是光滑的，还需要满足周期性边界条件。（这些性质的证明见例如文献[2]。关键在于，那些收敛速率与边界条件无关的基函数是奇异Sturm-Liouville方程的解。）正是这种对边界条件细节的独立性，使得切比雪夫多项式等基函数显得“神奇”。

切比雪夫多项式广受欢迎的另一个原因是，它们本质上只是三角函数，其自变量 $\theta$ 通过变换 $x=\cos \theta$ 映射而来：

$$T_n(x)=\cos (n\theta ),x=\cos \theta$$

因此，切比雪夫多项式展开可以通过快速傅里叶变换（FFT）高效求值。此外，此类展开的导数也可以通过FFT技术计算，如下文所述。

对于球形区域，球谐函数是 $\cos \theta$ 的勒让德函数与 $\varphi$ 方向上的傅里叶级数的乘积。同样，对于光滑函数，这种展开也能获得指数级收敛。

20.7.3 展开系数的计算

我们如何计算系数 $a_n$？有三种基本方法，可以通过将展开式（20.7.1）代入所求解的方程后考察残差来进行比较：

1. Tau方法：要求计算出的 $a_n$ 满足边界条件，并使残差尽可能与尽可能多的基函数正交。

2. Galerkin方法：将基函数组合成一组新的基函数，每个新基函数都满足边界条件，然后使残差尽可能与这些新基函数正交。（这本质上就是我们在求解偏微分方程时分离变量的做法，如我们在处理方程20.7.2时所做的那样。通常我们会从那些本身已满足边界条件的基函数开始。）

3. 配置法（或称拟谱方法）：与Tau方法类似，要求满足边界条件，但要求残差在一组适当选取的点上为零。

正如我们将看到的，拟谱方法还有一种替代解释，使其非常易于使用。因此，我们仅讨论这种方法，其他方法请参阅相关文献。

拟谱方法的一大优势在于它易于用于非线性问题。与前两种方法不同，拟谱方法不直接处理谱系数，而是处理解在与基函数相关的特殊网格点（通常是高斯求积点）上的值。这些点称为配置点。我们通常说，我们是在物理空间中处理解，而不是在谱空间中。

拟谱方法是一种插值方法：将表达式

$$y(x)=\sum _{n=0}^N{a}_n{\varphi }_n(x)$$

视为一个插值多项式。要求该插值多项式在 $N+1$ 个配置点上精确等于真实解。如果我们操作得当，那么当 $N\to \infty$ 时，点之间的误差将以指数速度趋于零。

20.7.4 谱方法与高斯求积

回顾高斯求积公式（§4.6.1）：

$${\int }_a^{b}y(x)w(x)dx\approx \sum _{i=0}^N{w}_{i}y(x_i)$$

其中 $w(x)$ 是所谓的权函数，通常用于提取被积函数中的某些奇异行为，使 $y(x)$ 成为光滑函数。该公式通过选择 $2N+2$ 个权值 $w_i$ 和节点 $x_i$，使得公式对多项式 $1,x,x^2,\dots ,x^{2N+1}$ 精确成立。（注意不要混淆符号：$w_i$ 与 $w(x)$ 之间没有直接关系。）如§4.6所示，高斯求积与给定权函数下的正交多项式 ${\varphi }_n(x)$ 相关：

$$⟨{\varphi }_n|{\varphi }_m⟩\equiv {\int }_a^b{\varphi }_n(x){\varphi }_m(x)w(x)dx={\delta }_{mn}$$

节点 $x_i$ 恰好是 ${\varphi }_{N+1}(x)$ 的 $N+1$ 个根，而权值 $w_i$ 由公式（4.6.9）给出。

我们可以利用高斯求积来定义两个函数的离散内积：

$$⟨f|g{⟩}_{\mathrm{G}}=\sum _{i=0}^N{w}_{i}f(x_i)g(x_i)$$

此处下标 G 代表高斯（Gaussian）。

高斯求积的一个重要性质是离散正交关系：

$$⟨{\varphi }_n|{\varphi }_m{⟩}_{\mathrm{G}}={\delta }_{mn},m+n\le 2N+1$$

证明：式 (20.7.18) 是式 (20.7.16) 的高斯求积形式。根据假设，式 (20.7.16) 中的被积函数 ${\varphi }_n(x){\varphi }_m(x)$ 是一个次数为 $m+n\le 2N+1$ 的多项式。而高斯求积的构造保证了对次数 $\le 2N+1$ 的多项式能够精确积分。证毕。

现在假设我们用拟谱插值多项式来近似 $y(x)$：

$$P_N(x)=\sum _{n=0}^N{\bar{a}}_n{\varphi }_n(x)$$

其中配置点选为高斯求积点：

$$P_N(x_i)=\gamma (x_i),i=0,1,\dots ,N$$

这总是可行的，因为通过 $N+1$ 个点的插值多项式是一个次数为 $N$ 的多项式，而函数 ${\varphi }_0(x),\dots ,{\varphi }_N(x)$ 构成了这类多项式的一组基。一个或许出人意料的结果是，展开式 (20.7.19) 中的系数 $\{{\overline{a}}_n\}$ 可由高斯求积精确给出：

$${\bar{a}}_n=⟨y|{\varphi }_n{⟩}_{\mathrm{G}}$$

要看出这一点，将式 (20.7.19) 两边与 ${\varphi }_m$ 取离散内积：

$$⟨P_N|{\varphi }_m{⟩}_{\mathrm{G}}=\sum _{n=0}^N{\overline{a}}_n⟨{\varphi }_n|{\varphi }_m{⟩}_{\mathrm{G}}$$

若使用离散正交关系 (20.7.18)，右边即为 ${\overline{a}}_m$。在左边，由于 $P_N$ 是插值多项式，我们可以在高斯求积中用 $y(x_i)$ 替换 $P_N(x_i)$。因此结论成立。

现在进入关键点。函数 $y(x)$ 的真实谱展开为：

$$y(x)=\sum _{n=0}^{\infty }{a}_n{\varphi }_n(x)$$

其中精确的谱系数为：

$$a_n=⟨y|{\varphi }_n⟩={\int }_a^{b}y(x){\varphi }_n(x)w(x)dx$$

拟谱展开系数 ${\overline{a}}_n$ 是插值多项式 $P_N(x)$（即式 (20.7.19)）的精确展开系数。精确谱系数与拟谱展开系数之间的关系可由式 (20.7.21) 推出：

$$\begin{array}{rl}& {\bar{a}}_n=⟨y|{\varphi }_n{⟩}_{\mathrm{G}}\\ & =\sum _{m=0}^{\infty }{a}_m⟨{\varphi }_m|{\varphi }_n{⟩}_{\mathrm{G}}(\text{使用式 20.7.23})\\ & =\sum _{m=0}^N{a}_m⟨{\varphi }_m|{\varphi }_n{⟩}_{\mathrm{G}}+\sum _{m>N}{a}_m⟨{\varphi }_m|{\varphi }_n{⟩}_{\mathrm{G}}\\ & =a_n+\sum _{m>N}{a}_m⟨{\varphi }_m|{\varphi }_n{⟩}_{\mathrm{G}}\end{array}$$

因此，由于当 $N$ 很大时，精确谱系数能对 $y(x)$ 给出指数级精度的逼近，拟谱系数同样也能做到这一点。顺便提一下，这也正是“拟谱方法”（pseudospectral method）这一名称的由来：我们使用的系数并非真实的谱系数，但与之非常接近。从现在起，我们将不再区分这两组系数，而统一用 $a_n$ 表示 $a_n$ 或 ${\overline{a}}_n$。

高斯求积的配置点，即 ${\varphi }_{N+1}(x)$ 的根，全部位于区间 $(a,b)$ 内部，远离端点。还存在另一种包含区间两个端点的高斯求积形式，称为高斯-洛巴托求积（Gauss-Lobatto quadrature），其配置点即为高斯-洛巴托点（§4.6.4）。这些点与普通高斯点同样有效，并且在需要在端点施加边界条件时更为方便。

稍作离题：你可能误以为高斯积分相较于等距节点积分的唯一优势在于其代数精度为 $2N+1$，而等距节点积分在仅有 $N+1$ 个权重的情况下最多只能达到 $N$ 阶精度。然而事实上，高斯积分的主要优势在于：对于光滑函数，其收敛速度随 $N$ 呈指数级增长。这一点可从上述公式中令式 (20.7.21) 中 $m=0$ 显式看出：

$${\bar{a}}_0={\varphi }_0\sum _{i=0}^N{w}_{i}y(x_i)$$

其中 ${\varphi }_0$ 为常数。而该式按前述结论指数收敛于式 (20.7.24) 给出的表达式：

$$a_0={\varphi }_0{\int }_a^{b}y(x)w(x)dx$$

傅里叶级数如何融入这一讨论呢？毕竟，其配置点是等距的（通常取 $x_j=2\pi j/N$，$j=0,\dots ,N-1$）。但实际上，若将傅里叶级数视为用三角多项式对 $y(x)$ 进行插值，这些点正是正确的配置点。对应的高斯求积（使用等距点）即为中点法则（midpoint rule），而包含端点的高斯-洛巴托求积则对应于梯形法则（trapezoidal rule）。教科书会告诉你中点法则和梯形法则是低阶方法——这对任意函数而言确实如此。但若将其应用于周期函数（§5.8.1）或在无穷远处快速衰减的函数（§4.5 和 §13.11），它们实际上也具有指数收敛性，正如任何自洽的高斯求积方法所应有的那样。

20.7.5 基函数（Cardinal Functions）

你可以将任意关于函数 $f(x)$ 的多项式插值公式写成如下形式：

$$P_N(x)=\sum _{i=0}^{N}f(x_i)C_i(x)$$

其中 $C_i(x)$ 被称为基数函数（cardinal functions）。它们是次数为 $N$ 的多项式，并满足

$$C_i\left(x_j\right)={\delta }_{ij}$$

即，$C_i(x)$ 在第 $i$ 个配置点（collocation point）处取值为 1，而在所有其他配置点处取值为 0。

基数函数的一种显式表达式来自拉格朗日插值公式（参见公式 3.2.1）：

$$C_i\left(x\right)=\prod _{\begin{array}{c}j=0\\ j\ne i\end{array}}^N\frac{x-x_j}{x_i-x_j}$$

若将此式代入公式 (20.7.28)，即得到拉格朗日插值公式。每一种基函数的选择都对应于一种配置点 $x_j$ 的选择，从而通过公式 (20.7.30) 对应一种基数函数的选择。

还有其他等价的方式来表示 $C_i(x)$。例如，若 ${\varphi }_n(x)$ 是一组正交多项式，且配置点是 ${\varphi }_{N+1}(x)$ 的零点（即高斯求积点），那么 $C_i(x)$ 几乎就是 ${\varphi }_{N+1}(x)$，只是 ${\varphi }_{N+1}(x)$ 在所有网格点处都为零。由于在 $x=x_i$ 附近有

$${\varphi }_{N+1}(x)={\varphi }_{N+1}(x_i)+(x-x_i){\varphi }_{N+1}^{\prime }(x_i)+\cdots$$

我们可以通过除去 $x=x_i$ 处的零点来得到基数函数：

$$C_i\left(x\right)=\frac{{\varphi }_{N+1}\left(x\right)}{\left(x-x_i\right){\varphi }_{N+1}^{\prime }\left(x_i\right)}$$

在实际应用中，你并不需要记住像公式 (20.7.30) 或 (20.7.32) 这样的具体表达式。参考文献中的书籍已经为所有标准基函数列出了对应的 $C_i(x)$ 公式，如果你感兴趣的话。你真正需要的是基数函数的导数，即微分矩阵（differentiation matrices，见下文）。

你可能会对使用非常高阶的多项式插值来表示你的解感到担忧，特别是如果你曾遇到过龙格现象（Runge phenomenon）：如果网格点是等间距分布的，那么当 $N\to \infty$ 时，$P_N(x)$ 的误差可能会趋于无穷大。实际上，这种误差主要出现在区间端点附近——区间中部的表现还是不错的。解决方法是让网格点在端点附近更加密集，而这正是选择高斯点所实现的效果。这也是为什么在普通多项式逼近失效时，切比雪夫逼近（Chebyshev approximation）往往仍然有效的原因，正如 §5.8.1 中所讨论的那样。

20.7.6 谱方法表示与网格点表示的对比

让我们对比一下方程

$$\mathcal{L}\gamma =f$$

在谱空间（spectral space）和物理空间（physical space）中的解的表示方式。为简化起见，假设 $\mathcal{L}$ 是一个线性微分算子。

$$\begin{array}{rlr}& \text{谱空间}& \text{物理空间}\\ & y(x)={\sum }_{n=0}^N{a}_n{\varphi }_n(x)& y(x)={\sum }_{j=0}^N{y}_j{C}_j(x)\\ & {\sum }_{n=0}^N{a}_n\mathcal{L}{\varphi }_n(x)=f(x)& {\sum }_{j=0}^N{y}_j\mathcal{L}{C}_j(x)=f(x)\end{array}$$

仅在配置点处施加条件：

$$\sum _{n=0}^N{a}_n\mathcal{L}{\varphi }_n(x_j)=f(x_j)\sum _{j=0}^N{y}_j\mathcal{L}{C}_j(x_i)=f(x_i)$$

$$\text{即}\mathbf{La}=\mathbf{f},\text{其中}{L}_{jn}=\mathcal{L}{\varphi }_n(x_j)\text{即}{\mathbf{L}}^{(c)}\mathbf{y}=\mathbf{f},\text{其中}{L}_{ij}^{(c)}=\mathcal{L}{C}_j(x_i)$$

这两种表示方式之间的关系如下：从网格点值转换到谱系数，需将 $y(x)$ 沿每个基函数进行投影：

$$\begin{array}{rl}& a_i=⟨{\varphi }_i\mid y⟩\\ & ={\sum }_j{w}_j{\varphi }_i(x_j)y_j\text{（通过高斯求积计算积分）}(\mathrm{20.7.34})\end{array}$$

即

$$\mathbf{a}=\mathbf{M}\cdot \mathbf{y},\text{其中}{M}_{ij}={\varphi }_i(x_j)w_j$$

因此，谱空间中的关系 $\mathbf{L}\cdot \mathbf{a}=\mathbf{f}$ 变为 $\mathbf{L}\cdot \mathbf{M}\cdot \mathbf{y}=\mathbf{f}$。而在物理空间中为 ${\mathbf{L}}^{(c)}\cdot \mathbf{y}=\mathbf{f}$，故有

$${\mathbf{L}}^{(c)}=\mathbf{L}\cdot \mathbf{M}$$

其逆关系为

$$\mathbf{L}={\mathbf{L}}^{(c)}\cdot {\mathbf{M}}^{-1}$$

还需注意，公式 (20.7.34) 意味着

$$\mathbf{y}={\mathbf{M}}^{-1}\cdot \mathbf{a}$$

由于 $y=\sum a_n{\varphi }_n$，我们看到 ${\mathbf{M}}^{-1}$ 是将谱级数求和以得到网格点值的矩阵，即

$$M_{ij}^{-1}={\varphi }_j(x_i)$$

你可以验证这些关系是一致的：

$$\begin{array}{rl}& (\mathbf{M}\cdot {\mathbf{M}}^{-1}{)}_{ij}={\sum }_k{M}_{ik}{M}_{kj}^{-1}\\ & ={\sum }_k[{\varphi }_i(x_k)w_k][{\varphi }_j(x_k)]\\ & =⟨{\varphi }_i|{\varphi }_j{⟩}_{\mathrm{G}}\\ & ={\delta }_{ij}\text{(由离散正交性)}\end{array}$$

在实际应用中，若 $N$ 较大，变换 (20.7.35) 和 (20.7.38) 通常使用 FFT（快速傅里叶变换）来处理傅里叶或切比雪夫基函数。对于简单的程序，直接进行矩阵乘法即可。

20.7.7 微分矩阵

我们上面已经看到，伪谱方法的关键在于构造

$$L_{ij}^{(c)}=\mathcal{L}{C}_j(x_i)$$

这涉及在配置点处对基数函数求导。考虑一阶导数 ${\partial }_x$，此时需要矩阵

$$D_{ij}^{(1)}={\partial }_x{C}_j(x_i)$$

该量可以预先计算并存储。然后，要计算网格点处的一阶导数值向量，只需进行一次矩阵乘法：

$$\frac{\partial y}{\partial x}⟷\sum _{j=0}^N{D}_{ij}^{(1)}{y}_j$$

类似地，也可以定义二阶导数矩阵 $D_{ij}^{(2)}$，依此类推。

方程 (20.7.43) 中的矩阵乘法需要 $O(N^2)$ 次运算。对于傅里叶基函数 $e^{ikx}$，也可以采用如下替代方法计算导数：

$$\begin{array}{c}y\stackrel{\mathrm{FFT}}{\to }a\\ a⟶ika\\ ika\stackrel{\mathrm{inverse}\mathrm{FFT}}{\to }{y}^{\prime }\end{array}$$

对于切比雪夫基函数，在中间步骤存在一个简单的 $O(N)$ 递推关系，可以从函数的系数得到导数的系数（见公式 5.9.2）。因此整个过程的复杂度为 $O(N\log N)$。然而，只有当 $N\gtrsim 16\text{–}128$ 时（具体取决于计算机），这种方法才通常比 $O(N^2)$ 的矩阵乘法更快。因此，对于简单程序，直接使用矩阵乘法即可。

值得指出的是，这种利用递推关系在谱空间中计算算子的思想，远比切比雪夫函数导数这一简单例子更为普遍。当算子包含坐标简单幂次乘以导数时，该方法对高效生产代码至关重要。详情请参阅相关文献。

20.7.8 微分矩阵的计算

计算微分矩阵有以下几种选择：

1. 通过对拉格朗日多项式表示 (20.7.30) 求导推导公式。
2. 对基函数表示 (20.7.32) 求导。
3. 查阅已为各种基函数推导出的显式公式，例如参考文献 [3] 的第 2 章。
4. 使用下面给出的例程，该例程基于文献 [6] 中的方法。该算法仅需一组配置点 $\{x_i\}$，即可计算任意阶微分矩阵。

显然，最后一种选择最简单。然而，对于高精度计算，它可能存在舍入误差大于必要值的缺点。若存在此问题，请参阅文献 [7]。

weights.h

void weights(const Doub z, VecDoub_I &x, MatDoub_O &c)

计算伪谱配置法的微分矩阵。输入参数为 z（待计算矩阵的位置）和 x[0..n]（共 $n+1$ 个网格点）。输出 c[0..n][0..n] 包含在网格点 x[0..n] 处对 0 至 $m$ 阶导数的权重。元素 c[j][k] 表示当使用 $n+1$ 个配置点 x 近似第 $k$ 阶导数时，需作用于 x[j] 处函数值的权重。注意，零阶导数矩阵的元素存储在 c[0..n][0] 中，即基数函数的值，也就是插值的权重。

Int n = c.nrows() - 1;
Int m = c.ncols() - 1;
Doub c1 = 1.0;
Doub c4 = x[0] - z;
for (Int k = 0; k <= m; k++)
    for (Int j = 0; j <= n; j++)
        c[j][k] = 0.0;
c[0][0] = 1.0;
for (Int i = 1; i <= n; i++) {
    Int mn = MIN(i, m);
    Doub c2 = 1.0;
    Doub c5 = c4;
    c4 = x[i] - z;
    for (Int j = 0; j < i; j++) {
        Doub c3 = x[i] - x[j];
        c2 = c2 * c3;
        if (j == i - 1) {
            for (Int k = mn; k > 0; k--)
                c[i][k] = c1 * (k * c[i-1][k-1] - c5 * c[i-1][k]) / c2;
            c[i][0] = -c1 * c5 * c[i-1][0] / c2;
        }
        for (Int k = mn; k > 0; k--)
            c[j][k] = (c4 * c[j][k] - k * c[j][k-1]) / c3;
        c[j][0] = c4 * c[j][0] / c3;
    }
    c1 = c2;
}

计算一阶和二阶导数矩阵时，weights 例程的典型用法如下：

VecDoub x(n);
MatDoub c(n,3), d1(n,n), d2(n,n);
for (j = 0; j < n; j++)
    x[j] = ...;
for (i = 0; i < n; i++) {
    weights(x[i], x, c);
    for (j = 0; j < n; j++) {
        d1[i][j] = c[j][1];
        d2[i][j] = c[j][2];
    }
}

20.7.9 关于插值的说明

通常，你希望在非配置点处对解进行求值，这就需要插值。为了保持完整的谱精度，你需要利用解中的全部信息。然而，并不需要将解变换到谱空间，再通过 Clenshaw 方法等在目标点处计算表达式 (20.7.1)。只需使用插值公式 (20.7.28) 即可。一种简单的方法是使用上述例程：当代码中 $\mathfrak{c}$ 的第二维 $\mathfrak{m}$ 为零时，该例程会返回任意目标点集 $x_k$ 对应的插值权重 $C_i(x_k)$。因此，向一组点插值仍可表示为矩阵乘法。

20.7.10 伪谱配置法作为一种有限差分方法

考虑在等距网格中心处对 $d/dx$ 的有限差分近似，例如：

$$\begin{array}{rl}h{f}^{\prime }(x)& =-\frac{1}{2}f(x-h)+\frac{1}{2}f(x+h)+O(h^2)\\ & =\frac{1}{12}f(x-2h)-\frac{2}{3}f(x-h)+\frac{2}{3}f(x+h)-\frac{1}{12}f(x+2h)+O(h^4)\\ & =\dots \end{array}\text{\hspace{1em}(2c)}$$

对于这类中心差分格式，当 $N\to \infty$ 时，权重（即 $f$ 的系数）的极限是有限的。但对于单边或部分单边近似，权重会发散 [5]。由于在网格端点附近必须使用此类近似，因此高阶有限差分方法在边界附近出现较大误差也就不足为奇了。

但假设网格点不是等距分布的，特别是像高斯求积点那样在端点附近更密集。此时，当 $N\to \infty$ 时，有限差分近似是收敛的。

伪谱方法给出的是通过 $N+1$ 个网格点数据的插值多项式的精确导数。若有限差分方法使用全部 $N+1$ 个网格点，也会得到相同结果。这是因为通过全部 $N+1$ 个点的插值多项式是唯一的，即一个次数为 $N$ 的多项式。

从这一观点出发，可将伪谱方法视为一种在网格点上获得高阶数值导数近似的方法。然后，就像有限差分方法一样，在网格点上满足所要求解的方程。

20.7.11 变系数与非线性项

假设方程中包含形如 $\sinh (x)y(x)$ 的项。无需将 $\sinh (x)$ 展开为基函数——只需在每个配置点处将 $\sinh (x)$ 与 $y$ 相乘即可。类似地，非线性项如 $y^2$ 也可直接利用配置点处的值进行计算。这是相对于 tau 方法和 Galerkin 方法的一大优势——在物理空间而非谱空间处理非线性项要容易得多。

20.7.12 一个详细示例

以下是一个简单的一维例子，取自文献 [5] 的附录 B。考虑方程：

$$\begin{array}{r}{y}^{\prime \prime }+y^{\prime }-2y+2=0,-1\le x\le 1,\\ y(-1)=y(1)=0\end{array}$$

其精确解为：

$$y(x)=1-\frac{e^x\sinh 2+e^{-2x}\sinh 1}{\sinh 3}$$

我们采用 $N=4$ 的 Chebyshev 多项式展开：

$$y=\sum _{n=0}^4{a}_n{T}_n(x)$$

选择配置点为：

$$x_i=-\cos \frac{i\pi }{4},i=0,\dots ,4$$

这些是与 Chebyshev 多项式相关的 Gauss-Lobatto 点，即包含端点。当我们需要施加 Dirichlet 边界条件（即边界上的函数值）时，总是包含端点。

利用某种方法构造微分矩阵，可得：

$$[D^{(1)}y{]}_i=\left[\begin{array}{ccccc}-\frac{11}{2}& 4+2\sqrt{2}& -2& 4-2\sqrt{2}& -\frac{1}{2}\\ -1-\frac{1}{2}\sqrt{2}& \frac{1}{2}\sqrt{2}& \sqrt{2}& -\frac{1}{2}\sqrt{2}& 1-\frac{1}{2}\sqrt{2}\\ \frac{1}{2}& -\sqrt{2}& 0& \sqrt{2}& -\frac{1}{2}\\ -1+\frac{1}{2}\sqrt{2}& \frac{1}{2}\sqrt{2}& -\sqrt{2}& -\frac{1}{2}\sqrt{2}& 1+\frac{1}{2}\sqrt{2}\\ \frac{1}{2}& -4+2\sqrt{2}& 2& -4-2\sqrt{2}& \frac{11}{2}\end{array}\right]\left[\begin{array}{c}{y}_0\\ y_1\\ y_2\\ y_3\\ y_4\end{array}\right]$$

以及

$$[D^{(2)}y{]}_i=\left[\begin{array}{ccccc}17& -20-6\sqrt{2}& 18& -20+6\sqrt{2}& 5\\ 5+3\sqrt{2}& -14& 6& -2& 5-3\sqrt{2}\\ -1& 4& -6& 4& -1\\ 5-3\sqrt{2}& -2& 6& -14& 5+3\sqrt{2}\\ 5& -20+6\sqrt{2}& 18& -20-6\sqrt{2}& 17\end{array}\right]\left[\begin{array}{c}{y}_0\\ y_1\\ y_2\\ y_3\\ y_4\end{array}\right]$$

要求微分方程在内部配置点 $x_k$（$k=1,2,3$）处成立，对应使用上述矩阵的中间三行。施加边界条件 $y_0=y_4=0$ 意味着无需使用第一列和最后一列。因此，方程 (20.7.45) 给出：

$$\left[\begin{array}{ccc}-16+\frac{1}{2}\sqrt{2}& 6+\sqrt{2}& -2-\frac{1}{2}\sqrt{2}\\ 4-\sqrt{2}& -8& 4+\sqrt{2}\\ -2+\frac{1}{2}\sqrt{2}& 6-\sqrt{2}& -16-\frac{1}{2}\sqrt{2}\end{array}\right]\left[\begin{array}{c}{y}_1\\ y_2\\ y_3\end{array}\right]=\left[\begin{array}{c}-2\\ -2\\ -2\end{array}\right]$$

其解为

$$\left[\begin{array}{l}{y}_1\\ y_2\\ y_3\end{array}\right]=\left[\begin{array}{l}\frac{101}{350}+\frac{13}{350}\sqrt{2}\\ \frac{13}{25}\\ \frac{101}{350}-\frac{13}{350}\sqrt{2}\end{array}\right]$$

精确解（20.7.47）例如给出 $y(x=0)=0.52065$，而 $y_2=0.52000$。对于仅五个网格点而言，结果已经相当不错！然而关键在于，当 $N=16$ 时，误差约为 $10^{-16}$。若采用二阶有限差分格式，随着 $N$ 的这种增加，误差仅能减少约10倍左右。

20.7.13 多维谱方法

对于含时问题，最简单的方法是线法（method of lines）。将解展开为

$$y(t,x)=\sum _j{C}_j(x)y_j(t)$$

其中系数 $y_j$ 现在是时间的函数。于是有

$${\frac{\partial y}{\partial t}|}_i={\dot{y}}_i,{\frac{\partial y}{\partial x}|}_i=\sum _j{D}_{ij}^{(1)}{y}_j,etc.$$

由此得到关于 $y_j$ 的常微分方程组（ODEs），可用标准方法求解。龙格-库塔法（Runge-Kutta）是一个不错的起点。

对于二维或三维空间问题，通常对每个空间维度分别进行展开：

$$u(x,y,z)=\sum _{i,j,k}{u}_{ijk}{C}_i(x)C_j(y)C_k(z)$$

椭圆型方程会导出关于系数的联立代数方程组，由于变量数目庞大，通常采用迭代法求解。参见文献[11]中的示例及更多参考文献。

参考文献

Hesthaven, J., Gottlieb, S., and Gottlieb, D. 2007, Spectral Methods for Time-Dependent Problems (New York: Cambridge University Press), Chapter 9.[1]

Gottlieb, D., and Orszag, S.A. 1977, Numerical Analysis of Spectral Methods: Theory and Applications (Philadelphia: S.I.A.M.).[2] [经典著作，至今仍有一定参考价值。]

Canuto, C., Hussaini, M.Y., Quarteroni, A., and Zang, T.A. 1988, Spectral Methods in Fluid Dynamics (Berlin: Springer).[3] [流体动力学应用的标准参考书，但也适用于其他领域。]

Boyd, J.P. 2001, Chebyshev and Fourier Spectral Methods, 2nd ed. (New York: Dover Publications). 可在 http://www-personal.engin.umich.edu/~jpboyd 获取。[4] [最佳单本著作：内容全面且不过于形式化。]

Fornberg, B. 1996, A Practical Guide to Pseudospectral Methods (New York: Cambridge University Press).[5] [适合入门，但不适用于大规模问题。]

Fornberg, B. 1998, "Calculation of Weights in Finite Difference Formulas," SIAM Review vol. 40, pp. 685–691.[6]

Baltensperger, R., and Trummer, M.R. 2003, "Spectral Differencing with a Twist," SIAM Journal on Scientific Computing, vol. 24, pp. 1465–1487.[7]

Matsushima, T., and Marcus, P.S. 1995, "A Spectral Method for Polar Coordinates," Journal of Computational Physics vol. 120, pp. 365–374.[8]

Matsushima, T., and Marcus, P.S. 1997, "A Spectral Method for Unbounded Domains," Journal of Computational Physics vol. 137, pp. 321–345.[9]

Rawitscher, G.H. 1991, "Accuracy Analysis of a Bessel Spectral Function Method for the Solution of Scattering Equations," Journal of Computational Physics vol. 94, pp. 81–101.[10]

Pfeiffer, H.P., Kidder, L.E., Scheel, M.A., and Teukolsky, S.A. 2003, "A Multidomain Spectral Method for Solving Elliptic Equations," Computer Physics Communications, vol. 152, pp. 253–273.[11]

Bjørhus, M. 1995, "The ODE Formulation of Hyperbolic PDEs Discretized by the Spectral Collocation Method," SIAM Journal on Scientific Computing, vol. 16, pp. 542–557. [描述了一种求解双曲型方程的良好算法。]