8.0 引言
本章内容几乎不属于一本关于数值方法的书籍:排序与选择是计算机科学标准课程中的基础内容。然而,从科学计算的角度对排序技术进行一些回顾,将对后续章节有所帮助。我们可以开发一些标准接口供以后使用,同时也能说明模板在面向对象编程中的实用性。
在数值计算工作中,处理数据(无论是实验数据还是数值生成的数据)时经常需要进行排序。我们通常拥有一些表格或数值列表,其中包含一个或多个自变量(或控制变量)以及一个或多个因变量(或测量变量)。在不同情况下,我们可能希望根据这些变量中的某一个对数据进行排序。或者,我们可能只是希望找出某个数值列表的中位数或上四分位数值。(这类数值统称为分位数。)这项与排序密切相关的工作称为选择。
具体而言,本章将处理以下任务:
-
对一个数值数组进行排序,即按数值大小重新排列。
-
在对一个数组按数值大小重新排列的同时,对一个或多个附加数组执行相应的重排,以保持所有数组中元素之间的对应关系。
-
给定一个数组,为其生成一个索引表,即一个指针表,指出哪个数组元素在数值顺序中排第一,哪个排第二,依此类推。
-
给定一个数组,为其生成一个秩表,即一个表,指出第一个数组元素、第二个数组元素等各自的数值秩。
-
从一个数组中选出第 大的元素。
-
从一个数据流中单次遍历(即无需存储数据流以供后续处理)选出第 大的值,或估计任意分位数值。
-
给定一组等价关系,将其组织成等价类。
对于对 个元素进行排序这一基本任务,最好的算法所需的操作次数约为 的若干倍。算法设计者试图尽可能减小该估计式前面的常数。其中两种最好的算法是 Quicksort(§8.2),由无与伦比的 C.A.R. Hoare 发明,以及 Heapsort(§8.3),由 J.W.J. Williams 发明。
对于较大的 (例如 ),在大多数机器上,Quicksort 的速度比 Heapsort 快 1.5 到 2 倍;但它需要额外的少量内存,并且程序实现相对复杂一些。Heapsort 是一种真正的“原地排序”算法,程序实现更为紧凑,因此在特殊用途下稍容易修改。综合考虑,我们推荐使用 Quicksort,因其速度优势,但我们会同时实现这两种算法。
对于较小的 ,如果某个算法的操作次数随 的更高次幂(即更差的复杂度)增长,但其前面的常数足够小,则可能表现更好。大致而言,当 时,直接插入法(§8.1)简洁且足够快。我们怀着些许不安将其包含进来:它是一个 算法,若被误用于过大的 ,其潜在危害极大。由此造成的计算资源浪费可能非常严重,以至于我们曾考虑完全不包含任何 算法。不过,我们将明确排除一种低效的 算法——即基础计算机科学教材中钟爱的冒泡排序(bubble sort)。如果你知道冒泡排序是什么,请把它从脑海中彻底清除;如果你还不知道,请务必永远不要去了解!
大致而言,当 时,Shell 方法(§8.1)仅比直接插入法稍微复杂一点,但在许多机器上可与更复杂的 Quicksort 相媲美。该方法在最坏情况下的复杂度为 ,但通常更快。
关于排序的更多内容及详细文献参考,请参见文献 [1,2]。
参考文献
Knuth, D.E. 1997, Sorting and Searching, 3rd ed., vol. 3 of The Art of Computer Programming (Reading, MA: Addison-Wesley).[1]
Sedgewick, R. 1998, Algorithms in C, 3rd ed. (Reading, MA: Addison-Wesley), Chapters 8–13.[2]
8.1 直接插入法与 Shell 方法
直接插入法是一个 算法,仅应用于较小的 ,例如 。
该技术正是经验丰富的纸牌玩家用来整理手牌的方法:取出第二张牌,将其与第一张牌按顺序排列;然后取出第三张牌,将其插入前两张牌组成的序列中;依此类推,直到最后一张牌被取出并插入为止。
通过直接插入法将数组 arr[0..n-1] 按升序排列。输出时,arr 将被其排序后的重排结果所替代。
Int i, j, n = arr.size();
T a;
for (j = 1; j < n; j++) {
a = arr[j]; // 依次取出每个元素
i = j;
while (i > 0 && arr[i-1] > a) {
arr[i] = arr[i-1];
i--;
}
arr[i] = a; // 插入该元素
}
注意此处使用了模板,以使该例程适用于任何类型的 NRvector,包括 VecInt 和 VecDoub。向量中类型为 T 的元素唯一需要满足的条件是具有赋值运算符和 > 关系。(我们通常假定 <、> 和 == 关系均存在。)如果你试图对不满足这些性质的元素向量进行排序,编译器会报错,因此你不会出错。
在模板设计上,可以像上面那样对元素类型进行模板化,也可以对向量本身进行模板化,例如:
template<class T>
void piksrt(T &arr)
这看起来更通用,因为它适用于任何具有下标运算符 [] 的类型 T,而不仅限于 NRvector。然而,这也要求 T 提供某种方法来获取其元素的类型,以便声明变量 a。如果 T 遵循 STL 容器的惯例,则该声明可写作
T::value_type a;
但如果它没有定义,那么你可能会在 C 处迷失方向。
如果你还想在对数组 arr 排序的同时重新排列另一个数组 brr,该怎么办?只需在移动 arr 中某个元素的同时,也移动 brr 中对应的元素即可:
注意,arr 和 brr 的类型是分别模板化的,因此它们不必相同。
不要将此技术推广到通过排序其中一个数组来重新排列更多数组的情形。请参见 §8.4。
8.1.1 希尔排序法(Shell's Method)
这实际上是直接插入排序的一种变体,但确实是一种非常强大的变体。其基本思想如下(以排序 16 个数 为例):首先,用直接插入法对 8 个包含 2 个元素的组分别排序:()、()、、()。接着,对 4 个包含 4 个元素的组分别排序:()、、()。然后对 2 个包含 8 个记录的组排序,第一组为 ()。最后,对全部 16 个数进行排序。
当然,只有最后一次排序对于将数字排成顺序才是必需的。那么前面这些部分排序的目的是什么呢?答案是:前面的排序能让数字高效地“过滤”到接近其最终位置的地方。因此,在最后一次排序中进行直接插入时,通常只需比较“少数几个”元素就能找到正确的位置。(可以想象整理一副已经几乎有序的扑克牌。)
在每次遍历数据时,所排序元素之间的间距(在上述例子中为 8、4、2、1)称为增量(increments),希尔排序有时也被称为“递减增量排序”(diminishing increment sort)。关于如何选择一组好的增量序列已有大量研究,但最优选择仍未可知。事实上,序列 …, 8, 4, 2, 1 并不是一个好的选择,尤其当 是 2 的幂时更是如此。一个更好的选择是如下序列:
该序列可通过以下递推关系生成:
可以证明(见 [1]),对于该增量序列,即使原始数据处于最坏的排列顺序下,所需操作总数的阶为 。对于“随机”排列的数据,操作次数大约为 (至少在 时如此)。然而,当 时,快速排序通常更快。
使用希尔方法(递减增量排序)将数组 a[0..n-1] 按升序排列。输出时,a 将被其排序后的重排结果所替代。通常应省略可选参数 ,但如果将其设为正值,则仅对 a 的前 个元素进行排序。
Int i, j, inc, n = a.size();
T v;
if (m > 0) n = MIN(m, n);
inc = 1;
do {
inc *= 3;
inc++;
} while (inc <= n);
do {
inc /= 3;
for (i = inc; i < n; i++) {
v = a[i];
j = i;
while (a[j - inc] > v) {
a[j] = a[j - inc];
j -= inc;
if (j < inc) break;
}
a[j] = v;
}
} while (inc > 1);
参考文献
Knuth, D.E. 1997, Sorting and Searching, 3rd ed., vol. 3 of The Art of Computer Programming (Reading, MA: Addison-Wesley), §5.2.1.[1]
Sedgewick, R. 1998, Algorithms in C, 3rd ed. (Reading, MA: Addison-Wesley), Chapter 8.
8.2 快速排序(Quicksort)
在大多数机器上,对于较大的 ,快速排序在平均情况下是目前已知最快的排序算法。它是一种“划分-交换”排序方法:从数组中选出一个“划分元素” a。然后通过成对交换元素,将原数组划分为两个子数组。在一轮划分结束时,元素 a 位于其最终位置上。左子数组中的所有元素都 a,而右子数组中的所有元素都 a。接着,对左右两个子数组分别独立地重复此过程,依此类推。
划分过程通过选择某个元素(例如最左边的元素)作为划分元素 a 来实现。从数组开头向上扫描一个指针,直到找到一个大于 a 的元素;同时从数组末尾向下扫描另一个指针,直到找到一个小于 a 的元素。这两个元素显然在最终划分后的数组中位置错误,因此交换它们。重复此过程,直到两个指针交叉。此时就是插入 a 的正确位置,本轮划分完成。当遇到等于划分元素的元素时,最佳策略较为微妙;详见 Sedgewick [1] 的讨论。(答案是:应停止并执行交换。)
为了提高执行速度,我们并未使用递归实现快速排序。因此,该算法需要一个长度为 的辅助存储数组,用作下推栈(push-down stack)以跟踪待处理的子数组。当子数组的大小减小到某个值 时,使用直接插入排序(§8.1)会更快,因此我们将这样做。 的最优值依赖于具体机器,但 通常不会差得太远。有些人主张将短子数组留到末尾再统一进行一次大规模的插入排序。由于每个元素最多移动七个位置,这种做法与立即排序同样高效,并节省了递归开销。然而,在具有缓存层次结构的现代机器上,一次性处理大数组会带来额外开销。我们并未发现将插入排序推迟到末尾有任何优势。
如前所述,快速排序的平均运行时间很快,但其最坏情况下的运行时间可能非常慢:实际上,最坏情况下的时间复杂度是 !而且,对于最直接的快速排序实现,当输入数组已经有序时,恰恰会触发最坏情况!这种输入顺序在实践中很容易出现。一种避免方法是使用一个小型随机数生成器,随机选择一个元素作为划分元素。另一种方法是取当前子数组首、中、尾三个元素的中位数作为划分元素。
快速排序之所以极快,是因为其内层循环非常简洁高效。仅仅增加一个不必要的判断(例如检查指针是否越界),就几乎会使运行时间翻倍!为避免此类不必要的判断,可在被划分子数组的两端放置“哨兵”(sentinels):左端哨兵 a,右端哨兵 a。在使用“三数取中法”选择划分元素时,我们可以将未被选为中位数的另外两个元素用作该子数组的哨兵。
我们的实现紧密遵循 [1]:
static const Int M = 7, NSTACK = 64;
// M 是使用直接插入排序的子数组大小,NSTACK 是所需的辅助存储空间。
Int i, ir, j, k, jstack = -1, l = 0, n = arr.size();
T a;
VecInt istack(NSTACK);
if (m > 0) n = MIN(m, n);
ir = n - 1;
for (;;) {
if (ir - l < M) {
for (j = l + 1; j <= ir; j++) {
a = arr[j];
for (i = j - 1; i >= l; i--) {
if (arr[i] <= a) break;
arr[i + 1] = arr[i];
}
arr[i + 1] = a;
}
if (jstack < 0) break;
ir = istack[jstack--];
l = istack[jstack--];
} else {
k = (l + ir) >> 1;
SWAP(arr[k], arr[l + 1]);
if (arr[l] > arr[ir]) {
SWAP(arr[l], arr[ir]);
}
if (arr[l + 1] > arr[ir]) {
SWAP(arr[l + 1], arr[ir]);
}
if (arr[l] > arr[l + 1]) {
SWAP(arr[l], arr[l + 1]);
}
i = l + 1;
j = ir;
a = arr[l + 1];
arr[l + 1] = arr[j]; // 将中位数暂存到 l+1 位置
for (;;) {
do i++; while (arr[i] < a);
do j--; while (arr[j] > a);
if (j < i) break;
SWAP(arr[i], arr[j]);
}
arr[l + 1] = arr[j];
arr[j] = a;
jstack += 2;
// 将较大的子数组指针压入栈;立即处理较小的子数组。
if (jstack >= NSTACK) throw("NSTACK too small in sort.");
if (ir - i + 1 >= j - l) {
istack[jstack] = ir;
istack[jstack - 1] = i;
ir = j - 1;
} else {
istack[jstack] = j - 1;
istack[jstack - 1] = l;
l = i;
}
}
}
和往常一样,你可以在对 arr 排序的同时移动其他任何数组。为了避免重复啰嗦,这里再次强调:
template<class T, class U>
void sort2(NRvector<T> &arr, NRvector<U> &brr)
使用快速排序将数组 arr[0..n-1] 按升序排列,同时对数组 brr[0..n-1] 进行相应的重排。
{
const Int M = 7, NSTACK = 64;
Int i, ir, j, k, jstack = -1, l = 0, n = arr.size();
T a;
U b;
VecInt istack(NSTACK);
ir = n - 1;
for (;;) {
if (ir - l < M) {
for (j = l + 1; j <= ir; j++) {
a = arr[j];
b = brr[j];
for (i = j - 1; i >= l; i--) {
if (arr[i] <= a) break;
arr[i + 1] = arr[i];
brr[i + 1] = brr[i];
}
arr[i + 1] = a;
brr[i + 1] = b;
}
if (jstack < 0) break;
ir = istack[jstack--];
l = istack[jstack--];
} else {
// ...(其余快速排序逻辑,同时交换 brr 中对应元素)
}
}
if (jstack < 0) break;
ir = stack[jstack--];
l = stack[jstack--];
} else {
k = (l + ir) >> 1;
SWAP(arr[k], arr[l+1]);
SWAP(brr[k], brr[l+1]);
if (arr[l] > arr[ir]) {
SWAP(arr[l], arr[ir]);
SWAP(brr[l], brr[ir]);
}
if (arr[l] > arr[l+1]) {
SWAP(arr[l], arr[l+1]);
SWAP(brr[l], brr[l+1]);
}
if (arr[l+1] > arr[ir]) {
SWAP(arr[l+1], arr[ir]);
SWAP(brr[l+1], brr[ir]);
}
}
i = l + 1;
j = ir;
a = arr[l + 1]; // Initialize pointers for partitioning. // Partitioning element.
b = brr[l + 1];
for (;;) {
do i++; while (arr[i] < a);
do j--; while (arr[j] > a);
if (j < i) break;
SWAP(arr[i], arr[j]);
SWAP(brr[i], brr[j]);
}
arr[l + 1] = arr[j];
arr[j] = a;
brr[l + 1] = brr[j];
brr[j] = b;
jstack += 2;
// Push pointers to larger subarray on stack; process smaller subarray immediately.
if (jstack >= NSTACK) throw("NSTACK too small in sort2");
if (ir - i + 1 >= j - l) {
stack[jstack] = ir;
stack[jstack - 1] = i;
ir = j - 1;
} else {
stack[jstack] = j - 1;
stack[jstack - 1] = l;
l = i;
}
}
原则上,你可以同时对任意多个额外数组(与 brr 一起)进行重排,但如果这类数组的数量超过一个,这种做法效率不高。推荐的方法是使用索引表,如 §8.4 节所述。
Sedgewick, R. 1978, "Implementing Quicksort Programs," Communications of the ACM, vol. 21 pp. 847–857.[1]
8.3 堆排序(Heapsort)
堆排序比快速排序慢一个常数因子。它如此优美,以至于我们有时仍会使用它,纯粹是为了享受其美感。(不过,如果你的雇主要求编写高效的代码,我们并不推荐这样做。)堆排序是一种真正的“原地”排序算法,不需要任何辅助存储空间。它的时间复杂度为 ,不仅在平均情况下如此,在最坏情况下的输入数据顺序下也是如此。事实上,其最坏情况下的运行时间仅比平均情况差大约 20%。
详细阐述堆排序的理论超出了本书的范围。我们仅介绍其基本原理,然后推荐你参考文献 [1,2];或者,如果你想理解细节,也可以自行分析程序。
若一组 个数 (其中 )满足如下关系:
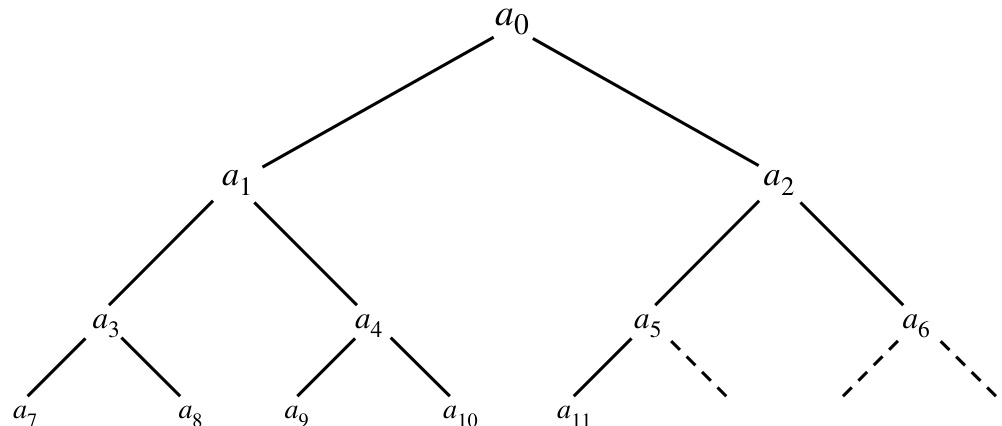
图 8.3.1. 由“堆”所隐含的顺序关系,此处为 12 个元素。通过向上路径相连的元素彼此有序,但仅“横向”相关的元素之间不一定有序。
此处 中的除法表示“整数除法”,即结果为精确整数,否则向下取整至最近的整数。如果你将这些数 想象成一棵二叉树的形式,其中顶部的“老板”节点为 ;其两个“下属”节点为 和 ;再下一层的四个下属节点为 到 ;依此类推(见图 8.3.1),那么定义 (8.3.1) 就很容易理解了。在这种结构中,堆的每个“主管”都大于或等于其两个“下属”,这种关系贯穿整个层级结构。
一旦你将数组重排成堆的形式,对其进行排序就非常简单了:你只需取出“堆顶”元素,它就是尚未排序元素中最大的一个。然后将堆中其最大的下属“提拔”到堆顶;接着再提拔该下属的最大下属,依此类推。这个过程类似于大型企业中董事会主席退休时所发生的情况(或理应发生的情况)。然后你重复整个过程,让新任董事会主席也“退休”。显然,整个过程的时间复杂度为 ,因为每次主席退休都会引发大约 次下属的提拔。
那么,最初如何将数组排列成堆呢?答案依然是类似于企业提拔的“筛下”(sift-up)过程。想象一家企业最初有 名员工在生产线上,但没有主管。现在招聘一名主管来管理两名工人。如果该主管的能力不如其中一名工人,那么该工人就被提拔取代主管的位置,而原主管则加入生产线。在主管被招聘之后,再招聘主管的主管,依此类推,直至企业高层。每位新员工最初都被置于树的顶部,但随即被“筛下”,更有能力的员工被不断提拔,直到达到其合适的职位层级。
在堆排序的实现中,相同的“筛下”代码既可用于初始建堆阶段,也可用于后续的“退休与提拔”阶段。一次堆排序函数的执行,就代表了一家巨型企业的完整生命周期:先招聘 名工人;再招聘 名潜在主管;随后在组织内进行一轮筛下过程,这类似于一种超级彼得原理(Peter Principle):最终,每位最初的员工都会被提拔为董事会主席。
namespace hpsort {
template<class T>
void sift_down(NRvector<T> &ra, const Int l, const Int r)
// 对元素 ra[l] 执行筛下操作以维持堆结构。l 和 r 确定筛下操作的“左”和“右”边界。
{
Int j, jold;
T a;
a = ra[l];
jold = l;
j = 2 * l + 1;
while (j <= r) {
if (j < r && ra[j] < ra[j+1]) j++;
if (a >= ra[j]) break;
ra[jold] = ra[j];
jold = j;
j = 2 * j + 1;
}
ra[jold] = a;
}
}
使用堆排序算法将数组 ra[0..n-1] 按升序排列。输出时,ra 将被替换为其排序后的重排结果。
在“招聘”(即建堆)阶段,索引 i(此处确定筛下操作的“左”边界,即待筛下的元素)从 n/2 - 1 递减至 0。
参考文献
Knuth, D.E. 1997, Sorting and Searching, 3rd ed., vol. 3 of The Art of Computer Programming (Reading, MA: Addison-Wesley), §5.2.3.[1]
Sedgewick, R. 1998, Algorithms in C, 3rd ed. (Reading, MA: Addison-Wesley), Chapter 11.[2]
8.4 索引与排序
(键)的概念在数据文件管理中起着重要作用。此类文件中的数据记录可能包含多个项(或字段)。例如,气象观测文件中的一条记录可能包含时间、温度和风速等字段。当我们对记录进行排序时,必须决定希望哪个字段处于排序后的顺序中,而记录中的其他字段则只是“搭便车”,通常不会形成任何特定的顺序。执行排序所依据的字段称为字段。
对于具有大量记录和字段的数据文件,将条记录按照其键()的实际顺序移动可能是一项艰巨的任务。取而代之的是,可以构建一个索引表(),使得最小的对应的,次小的对应,依此类推,直到最大的对应。换句话说,数组
在按索引时是有序的。当存在索引表时,无需将记录从其原始顺序中移动。此外,可以从同一组记录中创建不同的索引表,以针对不同的键进行索引。
构建索引表的算法非常直接:首先将索引数组初始化为从0到的整数;然后执行快速排序(Quicksort)算法,在排序过程中移动这些索引元素,就好像在对键进行排序一样。这样,最初对应最小键的整数最终会位于索引位置0,依此类推。
索引表的概念非常适合封装成一个对象,例如Indexxx。其构造函数接受一个向量arr作为参数;它会为arr生成一个索引表,而不会修改arr本身。随后,可以调用sort方法将arr或任何其他向量按照arr的排序顺序重新排列。Indexxx不是一个模板类,因为所存储的索引表不依赖于被索引向量的类型。然而,它确实需要一个模板化的构造函数。
struct Indexx {
Int n;
VecInt idx;
template<class T> Indexx(const NRvector<T> &arr) {
// 构造函数。调用 index 并存储对数组 arr[0..n-1] 的索引。
index(&arr[0], arr.size());
}
Indexx() {}
// 空构造函数。参见正文。
template<class T> void sort(NRvector<T> &brr) {
// 将数组 brr[0..n-1] 按照存储的索引顺序排序。
// 输出时,brr 被其排序后的重排结果替换。
if (brr.size() != n) throw("bad size in Index sort");
NRvector<T> tmp(brr);
for (Int j = 0; j < n; j++) brr[j] = tmp[idx[j]];
}
template<class T> inline const T & el(NRvector<T> &brr, Int j) const {
// 此函数(以及下一个)返回 brr 中根据存储索引应处于排序位置 j 的元素。
// 向量 brr 不会被修改。
return brr[idx[j]];
}
template<class T> inline T & el(NRvector<T> &brr, Int j) {
// 同上,但返回一个左值(l-value)。
return brr[idx[j]];
}
};
template<class T> void index(const T *arr, Int nn);
// 执行实际的索引工作。通常不直接由用户调用,但例外情况参见正文。
void rank(VecInt_0 &irank) {
// 返回一个秩表,其第 j 个元素是 arr[j] 的秩,
// 其中 arr 是最初被索引的向量。最小的 arr[j] 的秩为 0。
irank.resize(n);
for (Int j = 0; j < n; j++) irank[idx[j]] = j;
}
template<class T>
void Indexx::index(const T *arr, Int nn)
// 对数组 arr[0..nn-1] 建立索引,即调整 idx[0..nn-1] 的大小并设置其值,
// 使得 arr[idx[j]] 在 j = 0,1,...,nn-1 时按升序排列。
// 同时设置成员变量 n。输入数组 arr 不会被修改。
{
const Int M = 7, NSTACK = 64;
Int i, indext, j, k, jstack = -1, l = 0;
T a;
VecInt istack(NSTACK);
n = nn;
Int ir = n - 1;
for (j = 0; j < n; j++) idx[j] = j;
for (;;) {
if (ir - l < M) {
for (j = l + 1; j <= ir; j++) {
indext = idx[j];
a = arr[indext];
for (i = j - 1; i >= l; i--) {
if (arr[idx[i]] <= a) break;
idx[i + 1] = idx[i];
}
idx[i + 1] = indext;
}
if (jstack < 0) break;
ir = istack[jstack--];
l = istack[jstack--];
} else {
k = (l + ir) >> 1;
SWAP(idx[k], idx[l + 1]);
if (arr[idx[l]] > arr[idx[ir]]) {
SWAP(idx[l], idx[ir]);
}
if (arr[idx[l + 1]] > arr[idx[ir]]) {
SWAP(idx[l + 1], idx[ir]);
}
if (arr[idx[l]] > arr[idx[l + 1]]) {
SWAP(idx[l], idx[l + 1]);
}
i = l + 1;
j = ir;
indext = idx[l + 1];
a = arr[indext];
for (;;) {
do i++; while (arr[idx[i]] < a);
do j--; while (arr[idx[j]] > a);
if (j < i) break;
SWAP(idx[i], idx[j]);
}
idx[l + 1] = idx[j];
idx[j] = indext;
jstack += 2;
if (jstack >= NSTACK) throw("NSTACK too small in index");
if (ir - i + 1 >= j - l) {
istack[jstack] = ir;
istack[jstack - 1] = i;
ir = j - 1;
} else {
istack[jstack] = j - 1;
istack[jstack - 1] = l;
l = i;
}
}
}
}
Indexxx 的典型用法可能是将三个向量(不一定为相同类型)按照其中一个向量定义的顺序重新排列:
Indexx arrindex(arr);
arrindex.sort(arr);
arrindex.sort(brr);
arrindex.sort(crr);
推广到任意数量的数组是显而易见的。
Indexxx 对象还提供了一个名为 el(代表“element”)的方法,用于在不实际修改向量(或 arr 本身)的情况下,以 arr 排序后的顺序访问任意向量。换句话说,在对 arr 建立索引后,例如:
Indexx arrindex(arr);
我们可以简单地通过 arrindex.el(brr, j) 访问 arr 中对应于虚拟排序后第 j 个元素的值。arr 和 brr 都不会被改变。el 提供了两个版本,使其既可以作为左值(赋值语句左侧),也可以作为右值(表达式中使用)。
顺便提一下,内部核心函数 index 使用指针而非向量作为参数的原因是,它可以在其他场景中使用(严格主义者可能会说是“滥用”),例如对矩阵中某一行进行索引。这也是提供额外空构造函数的原因。如果你想对某个位置的 nn 个连续元素(由指针 ptr 指向)建立索引,可以这样写:
Indexx myhack;
myhack.index(ptr, nn);
秩表(rank table)与索引表不同。秩表的第 项给出原始键数组中第 个元素的秩,范围从 0(如果该元素是最小的)到 (如果该元素是最大的)。我们可以很容易地从索引表构造出秩表。事实上,你可能已经注意到 Indexxx 中有一个 rank 方法,它返回的就是这样一个表,并以向量形式存储。
图 8.4.1 总结了本节讨论的概念。
8.5 选择第 M 大的元素
选择是排序那严肃的姐妹。(快速说五遍!)排序要求对整个数据数组进行重新排列,而选择则礼貌地只要求返回一个单一的值:在 个元素中,第 小(或等价地,第 大)的元素是什么?(在本节通篇采用的约定中, 的取值为 ,因此 对应最小的数组元素,而 对应最大的元素。)不幸的是,最快的选值方法确实会为了自身的计算目的而重新排列数组,通常将所有较小的元素放在第 个元素的左侧,所有较大的元素放在右侧,并打乱每个子集内部的顺序。这种副作用充其量是无害的,最坏情况下则相当不便。当数组非常长,以至于制作一份副本会占用大量内存时,人们会转向无副作用的原地算法,尽管它们速度较慢,但不会破坏原始数组。
选择最常见的用途是对一组数据进行统计描述。人们常常想知道数组的中位数(分位数 )或上下四分位数(分位数 , )。当 为奇数时,中位数的精确定义是第 个元素,其中 。当 为偶数时,统计学教材将中位数定义为第 和 两个元素的算术平均值(即从底部数第 个和从顶部数第 个)。如果你坚持这种形式化定义,就必须执行两次独立的选择来找到这两个元素。(如果你第一次选择使用的是划分方法(见下文),那么第二次选择只需在右侧划分中对 个元素进行一次遍历,找出其中最小的元素即可。)对于 的情况,我们通常直接使用 作为中位数元素,管他形式主义者怎么说。
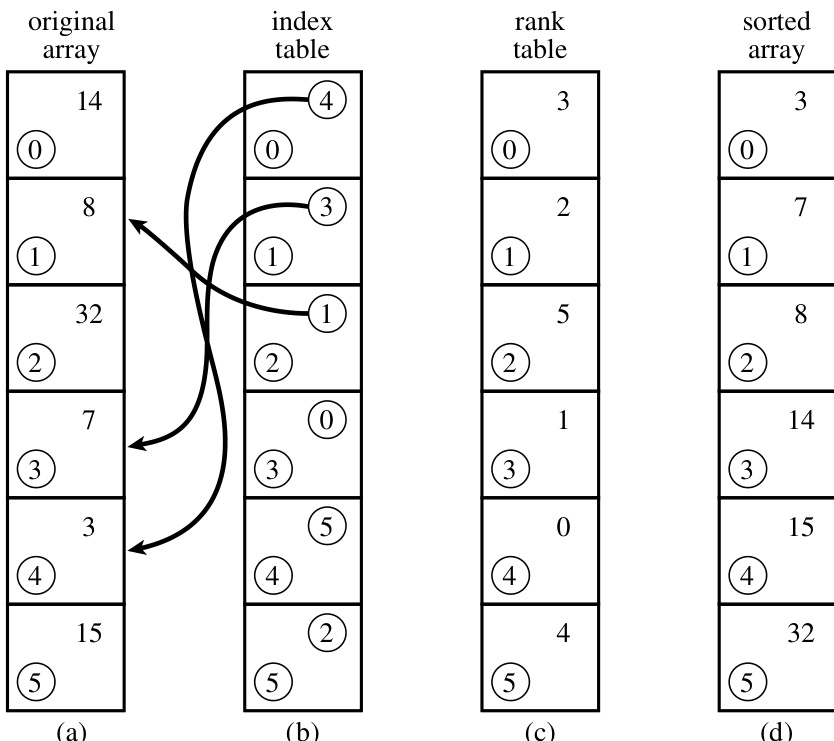
图 8.4.1. (a) 一个包含六个数字的未排序数组。(b) 索引表,其条目是指向 (a) 中元素的指针,按升序排列。(c) 秩表,其条目是 (a) 中对应元素的秩。(d) (a) 中元素的已排序数组。
对于大型数据集,选择的一种变体是单次遍历选择(single-pass selection),此时我们面对的是一个输入值流,每个值只能看到一次。我们希望在任意时刻(例如在处理了 个值之后)能够报告到目前为止看到的第 小(或最大)的值,或者等价地,某个分位数 对应的值。我们将描述两种方法:如果我们只关心最小(或最大)的 个值( 固定,因此 ),那么存在仅需 存储空间的优秀算法。另一方面,如果我们能接受近似答案,那么也存在高效的算法,可以在任意时刻对任意 ()给出 -分位数的良好估计。也就是说,我们得到的不是 个已处理值中精确的第 小元素(),而是非常接近它的某个值——而且无需 的存储空间,也无需事先知道 。
允许重新排列数组的最快通用选择方法是划分(partitioning),这与快速排序算法(§8.2)中所做的完全相同。选择一个“随机”的划分元素,遍历数组,将较小的元素强制移到左侧,较大的元素移到右侧。与快速排序一样,优化内层循环非常重要,使用“哨兵”(§8.2)可以最小化比较次数。对于排序,接下来需要对两个子集进一步划分;而对于选择,我们可以忽略其中一个子集,只关注包含所需第 个元素的那个子集。因此,基于划分的选择不需要维护待处理操作的栈,其操作次数与 成正比,而不是 (参见 [1])。与 §8.2 中的排序进行比较,应能清楚理解以下例程。
template<class T>
T select(const Int k, NRvector<T> &arr)
// 给定 k ∈ [0..n-1],返回 arr[0..n-1] 中的一个数组值,使得恰好有 k 个数组值小于或等于该返回值。
// 输入数组将被重新排列,使得该值位于 arr[k] 处,
// 所有较小的元素被移到 arr[0..k-1](顺序任意),
// 所有较大的元素被移到 arr[k+1..n-1](顺序任意)。
{
Int i, ir, j, l, mid, n = arr.size();
T a;
l = 0;
ir = n - 1;
for (;;) {
if (ir <= l + 1) {
if (ir == l + 1 && arr[ir] < arr[l]) SWAP(arr[l], arr[ir]);
return arr[k];
} else {
mid = (l + ir) >> 1;
SWAP(arr[mid], arr[l + 1]);
if (arr[l] > arr[ir]) SWAP(arr[l], arr[ir]);
if (arr[l + 1] > arr[ir]) SWAP(arr[l + 1], arr[ir]);
if (arr[l] > arr[l + 1]) SWAP(arr[l], arr[l + 1]);
i = l + 1;
j = ir;
a = arr[l + 1];
for (;;) {
do i++; while (arr[i] < a);
do j--; while (arr[j] > a);
if (j < i) break;
SWAP(arr[i], arr[j]);
}
SWAP(arr[l + 1], arr[j]);
if (j >= k) ir = j - 1;
if (j <= k) l = i;
}
}
}
如果你不希望数组 arr 被重新排列,那么在调用 select 之前应制作一份临时副本,例如:
VecDoub brr(arr);
select 内部不自动执行此操作的原因是,你可能希望用不同的 值多次调用 select,每次都复制向量将是浪费的;相反,只需让 brr 不断被重新排列即可。
8.5.1 单次遍历中跟踪最大的 个值
当然,select 不应用于查找数组中最大或最小元素这种平凡情况。这些情况你应该手工编写简单的 for 循环来实现。
当 被某个固定的 所限制( 相对于 较小,因此 的内存开销并不沉重)时,也有高效的编码方法。实际上, 甚至可能未知:你可能有一个传入的数据流,并需要在任意时刻提供到目前为止看到的最大的 个值的列表。
对此情况的一个好方法是使用堆排序(§8.3)的方法,维护一个包含 个最大值的堆。堆结构相对于长度为 的线性数组的优势在于,每次处理一个新数据值时,最多只需要 次操作,而不是 次。
Heapselect 对象有一个构造函数(用于指定 )、一个 add 方法(用于吸收新数据值)和一个 report 方法(用于获取到目前为止看到的第 大的值)。注意,report 的初始代价是 ,因为我们需要对堆进行排序;但之后你可以无额外代价地获取所有 值,直到下一次 add 操作。一个特例是获取第 大的值总是廉价的,因为它位于堆顶;因此,如果你有一个特别偏好的 值,最好选择 使得 。
struct Heapselect {
// 用于跟踪数据流中到目前为止看到的 m 个最大值的对象。
Int m, n, srtd;
VecDoub heap;
Heapselect(Int mm) : m(mm), n(0), srtd(0), heap(mm, 1.e99) {}
// 构造函数。参数是要跟踪的最大值个数。
void add(Doub val) {
// 吸收数据流中的一个新值。
Int j, k;
if (n < m) {
heap[n++] = val;
if (n == m) sort(heap);
} else {
if (val > heap[0]) {
heap[0] = val;
for (j = 0;;) {
k = (j << 1) + 1;
if (k > m - 1) break;
if (k != (m - 1) && heap[k] > heap[k + 1]) k++;
if (heap[j] <= heap[k]) break;
SWAP(heap[k], heap[j]);
j = k;
}
}
}
srtd = 0;
}
Doub report(Int k) {
// 返回到目前为止看到的第 k 大的值。
// k=0 返回最大值,k=1 返回第二大值,...,k=m-1 返回跟踪的最后一个位置。
// 此外,k 必须小于之前吸收的值的个数。
Int mm = MIN(n, m);
if (k > mm - 1) throw("Heapselect k too big");
if (k == m - 1) return heap[0];
if (!srtd) { sort(heap); srtd = 1; }
// 否则,需要对堆进行排序。
return heap[mm - 1 - k];
}
};
8.5.2 单次遍历中任意分位数的估计
数据值以流的形式飞速而过。你只能看每个值一次,并对其执行常数时间的处理(意味着你不能对后面的数据值花费越来越长的处理时间)。此外,你只有固定大小的存储内存。你时不时地想知道到目前为止所见数据的中位数(或第 95 百分位数,或任意 -分位数)。你该如何做到这一点?
显然,在上述条件下,你必须接受一个近似答案,因为精确答案必然需要无界的存储空间和(可能)无限的处理时间。如果你认为“分箱”(binning)是解决之道,你是对的。但如何选择箱子并不显而易见,因为你必须在看到潜在无限量的数据之后,才能确切知道其值的分布情况。
Chambers 等人 [2] 提出了一种鲁棒且极其快速的算法,他们称之为 agent,该算法能自适应地调整一组箱子,使其收敛到指定分位数 对应的数据值。其基本思想(见图 8.5.1)是将传入的数据累积成批次,然后通过添加批次的累积分布函数(cdf)并插值回一组固定的 -值,来更新存储的分段线性累积分布函数(cdf)。任意请求的分位数值(“增量分位数”,或“IQs”,因此得名)都可以通过在存储的 cdf 上进行线性插值得到。批处理使程序非常高效,每个新数据值的(摊销)代价仅为少量操作。批处理对用户是透明的。
与 Heapselect 类似,IQagent 对象也有 add 和 report 方法,后者现在以 值作为参数。在下面的实现中,我们使用批次大小 nbuf=1000,但每当请求分位数时,会使用部分批次进行一次提前更新。因此,在这些参数下,你应该在每处理几千个 nbuf 数据值后再请求分位数信息,此时你可以请求任意多个不同的 值。另一种选择是从 report 中移除对 update 的调用,这样你会得到快速但恒定的答案,仅在每次常规批次更新后才会改变。
IQagent 内部使用一组通用的 251 个 -值,包括从 10 到 90 的整数百分位点,以及一组对数间隔的小值和大值,覆盖范围从 到 。你请求的其他 -值通过插值得到。当然,在处理至少几倍于 个数据值之前,你无法获得小 值对应的有意义的尾部分位数。在此之前,程序只会报告之前看到的最小值(或对于 ,报告之前看到的最大值)。
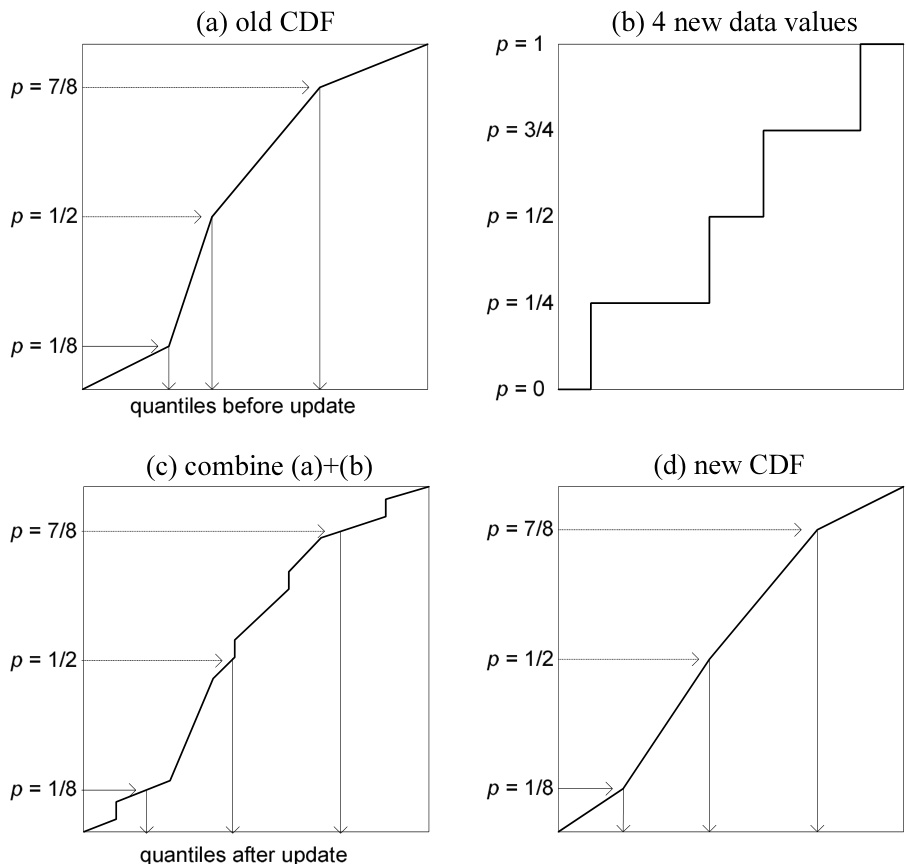
图 8.5.1. 更新分段线性累积分布函数(cdf)的算法。(a) cdf 由固定 -值(此处仅为 3 个)处的分位数值表示。(b) 一批新数据值(此处仅为 4 个)定义了一个阶梯状常数 cdf。(c) 两个 cdf 相加。新数据的阶梯相对于新批次大小与之前处理的数据量之比很小。(d) 通过对 (c) 在固定 -值处进行插值得到新的 cdf 表示。
// iqagent.h
struct IQagent {
static const Int nbuf = 1000;
Int nq, nt, nd;
VecDoub pval, dbuf, qile;
Doub q0, qm;
IQagent() : nq(251), nt(0), nd(0), pval(nq), dbuf(nbuf),
qile(nq, 0.), q0(1.e99), qm(-1.e99) {
// 构造函数。无参数。
// 设置通用的 p-值数组,范围从 10^{-6} 到 1-10^{-6}。你可以根据需要修改:
for (Int j = 85; j <= 165; j++) pval[j] = (j - 75.) / 100.;
for (Int j = 84; j >= 0; j--) {
pval[j] = 0.87191909 * pval[j + 1];
pval[250 - j] = 1. - pval[j];
}
}
};
void add(Doub datum) {
// 从数据流中吸收一个新值。
dbuf[nd++] = datum;
if (datum < q0) { q0 = datum; }
if (datum > qm) { qm = datum; }
if (nd == nbuf) update();
}
void update() {
// 批量更新,如图8.5.1所示。此函数由add或report调用,不应由用户直接调用。
Int jld = 0, jq = 1, iq;
Doub target, told = 0., tnew = 0., qold, qnew;
VecDoub newqile(nq);
sort = dbuf, nd;
qld = qnew = qile[0] = newqile[0] = q0;
qile[nq - 1] = newqile[nq - 1] = qm;
pval[0] = min(0.5 / (nt + nd), 0.5 * pval[1]);
// 并设置兼容的 $p$-值。
pval[nq - 1] = max(1. - 0.5 / (nt + nd), 0.5 * (1. + pval[nq - 2]));
for (iq = 1; iq < nq - 1; iq++) {
target = (nt + nd) * pval[iq];
if (tnew < target) {
for (;;) {
// 核心部分:我们定位一系列横纵坐标对 (qnew, tnew),
// 这些点对应于图8.5.1(c)中值或斜率的不连续点,
// 每当跨越一个目标点时,就进行插值。
if (jq < nq && (jld >= nd || qile[jq] < dbuf[jld])) {
// 找到旧CDF中的斜率不连续点。
qnew = qile[jq];
tnew = jld + nt * pval[jq++];
if (tnew >= target) break;
} else {
qnew = dbuf[jld];
tnew = told;
if (qile[jq] > qile[jq - 1])
tnew += nt * (pval[jq] - pval[jq - 1]) * (qnew - qold) / (qile[jq] - qile[jq - 1]);
jld++;
if (tnew >= target) break;
told = tnew;
qold = qnew;
}
}
}
// 跳转到这里并执行新的插值。
if (tnew == told)
newqile[iq] = 0.5 * (qold + qnew);
else
newqile[iq] = qold + (qnew - qold) * (target - told) / (tnew - told);
told = tnew;
qold = qnew;
}
qile = newqile;
nt += nd;
nd = 0;
}
Doub report(Doub p) {
// 返回迄今为止所见数据的p分位数估计值。(例如,p = 0.5 表示中位数。)
Doub q;
if (nd > 0) update();
Int jl = 0, jh = nq - 1, j;
while (jh - jl > 1) {
j = (jh + jl) >> 1;
if (p > pval[j]) jl = j;
else jh = j;
}
j = jl;
q = qile[j] + (qile[j + 1] - qile[j]) * (p - pval[j]) / (pval[j + 1] - pval[j]);
return MAX(qile[0], MIN(qile[nq - 1], q));
}
与将全部 个数据值存储在数组 中并报告“精确”分位数 相比,IQ agent 算法的精度如何?存在若干误差来源,你都可以通过修改 IQagent 中的参数加以控制。(我们认为默认参数对几乎所有用户都已足够好。)
首先,存在插值误差:目标累积分布函数(CDF)由 个存储值之间的分段线性函数表示。对于典型分布,这将精度限制在三到四位有效数字。我们很难相信有人需要比这更精确地知道中位数,但如果你确实需要,可以增加感兴趣区域中 -值的密度。
其次,还有统计误差。一种刻画这些误差的方法是:设 是最接近 IQ agent 报告分位数的值,那么 相对于 (即由有限样本量 所固有的精度)的比值有多小?如果该比值 ,则该估计是“足够好”的,意味着在给定你的样本下,没有任何方法能显著更好地估计总体分位数。
在默认参数下,对于行为合理的分布,IQagent 在 时通过该检验。对于更大的 ,统计误差变得显著(尽管通常仍小于上述插值误差)。不过,你可以通过增大批次大小 nbuf 来减小该误差。只要内存允许,并且你能接受排序时每个数据点对数级增长的计算开销,更大的 nbuf 总是更好的。
尽管 IQagent 的精度没有可证明的误差界保证,但该算法快速、鲁棒,强烈推荐使用。关于增量分位数估计的其他方法(包括一些提供可证明误差界的方法,但存在其他问题),参见 [3,4] 及其中引用的文献。
8.5.3 增量分位数估计的其他用途
增量分位数估计提供了一种有用的方法,可在不知道分箱边界的情况下,将数据直方图化为等频(每个箱包含相同数量点)但箱宽可变的箱子:首先,将 个数据值输入一个 IQagent 对象;然后,选择箱数 ,并定义
最后,若 是 处的分位数值,则第 个箱从 到 ,其高度为
另一种应用涉及监控分位数值的变化。例如,你可能在生产某种器件,其参数 的公差为 ,而你希望在观测到的 值在第5和第95百分位开始漂移时获得早期预警。
IQagent 对象很容易为此类应用进行修改。只需将 nt += nd 这一行改为 nt = myconstant,其中 myconstant 是你希望平均的历史器件数量。(更准确地说,该数值对应于对所有历史生产进行指数衰减加权平均时权重下降一个 倍的数量。)现在,存储的累积分布函数与新批次数据以恒定权重(而非递增权重)结合,你可以监控任意所需分位数随时间的变化。
8.5.4 原地选择
原地、非破坏性选择在概念上很简单,但需要大量簿记工作,因此相应地较慢。其基本思想是:随机选取 个元素,对其进行排序,然后遍历整个数组,统计有多少元素落入由这些元素定义的 个区间中。第 大的元素将落入其中一个区间——称之为“活跃”区间。接着进行第二轮:首先在活跃区间内随机选取 个元素,然后确定所有当前仍活跃的元素落入哪个新的、更细的 个区间中。如此反复,直到第 个元素最终被定位到一个大小为 的数组内,此时可直接进行选择。
我们应如何选取 ?轮数 随 增大而减小;但将每个元素定位到 个子区间中的工作量会增大,例如使用二分法时,其复杂度为 。每一轮都需要检查所有 个元素(至少要找出哪些仍处于活跃状态),而二分操作主要由第一轮的 次操作主导。因此,最小化 可得结果
由于对数的平方根变化极其缓慢,机器时序等次要因素变得重要。我们采用 作为方便的常数值。
更多讨论及代码见网络附注 [5]。
参考文献
Sedgewick, R. 1998, Algorithms in C, 3rd ed. (Reading, MA: Addison-Wesley), pp. 126ff.[1]
Knuth, D.E. 1997, Sorting and Searching, 3rd ed., vol. 3 of The Art of Computer Programming (Reading, MA: Addison-Wesley).
Chambers, J.M., James, D.A., Lambert, D., and Vander Wiel, S. 2006, "Monitoring Networked Applications with Incremental Quantiles," Statistical Science, vol. 21.[2]
Tierney, L. 1983, "A Space-efficient Recursive Procedure for Estimating a Quantile of an Unknown Distribution," SIAM Journal on Scientific and Statistical Computing, vol. 4, pp. 706-711.[3]
Liechty, J.C., Lin, D.K.J., and McDermott, J.P. 2003, "Single-Pass Low-Storage Arbitrary Quantile Estimation for Massive Datasets," Statistics and Computing, vol. 13, pp. 91–100.[4]
Numerical Recipes Software 2007, "Code Listing for Selip," Numerical Recipes Webnote No. 11, at http://www.nr.com/webnotes?11 [5]
8.6 等价类的确定
许多排序和搜索技术涉及一些数据结构,其细节超出了本书的范围,例如树、链表等。这些结构及其操作是计算机科学(而非数值分析)的核心内容,相关书籍不胜枚举。
在处理实验数据时,我们发现其中一种特定操作——即等价类的确定——出现得足够频繁,值得在此介绍。
问题如下:有 个“元素”(或“数据点”等),编号为 。你获得关于这些元素是否属于同一“相同性”等价类的成对信息,该“相同性”标准可任意定义。例如,你可能有一系列事实:“元素3和元素7属于同一类;元素19和元素4属于同一类;元素7和元素12属于同一类,……”。或者,你可能有一个过程,给定两个元素 和 的编号,可判定它们是否属于同一类。(回忆一下,等价关系可以是任何满足RST性质——自反性、对称性、传递性——的关系。这与任何直观的“相同性”定义兼容。)
期望的输出是对 个元素中的每一个分配一个等价类编号,使得两个元素属于同一等价类当且仅当它们被赋予相同的类编号。
高效的算法工作方式如下:设 为元素 所属的类或“家族”编号。初始时,每个元素各自构成一个家族,即 。数组 可以解释为一种树结构,其中 表示 的父节点。如果我们安排每个家族形成一棵独立的树,并与其他所有“家族树”互不相交,那么就可以用该树中最顶层的祖先(即最年长的曾曾……祖父)来标记每个家族(等价类)。树的具体拓扑结构完全无关紧要,只要将每个相关的元素以某种方式嫁接到该树上即可。
因此,对于每条基本关系“ 与 等价”,我们执行以下操作:(i) 沿着 向上追溯到其最高祖先;(ii) 沿着 向上追溯到其最高祖先;(iii) 将 的祖先设为 的子节点,或反之(两种方式效果相同)。在处理完所有关系后,我们遍历所有元素 ,并将它们的 更新为其可能的最高祖先,该祖先即为对应等价类的标签。
以下例程基于 Knuth[1] 的方法,假设有 条基本关系信息,存储在两个长度为 的数组 lista 和 listb 中,其含义是:对于 ,lista[j] 与 listb[j] 是两个(据称)相关的元素编号。
给定 个独立元素之间 对等价关系,以输入数组 lista[0..m-1] 和 listb[0..m-1] 的形式提供,该例程返回数组 nf[0..n-1],其中每个元素的等价类编号为介于 到 之间的整数(并非所有整数都会被使用)。
Int l, k, j, n = nf.size(), m = lsta.size();
for (k = 0; k < n; k++) nf[k] = k;
for (l = 0; l < m; l++) {
j = lsta[l];
while (nf[j] != j) j = nf[j];
k = listb[l];
while (nf[k] != k) k = nf[k];
if (j != k) nf[j] = k;
}
for (j = 0; j < n; j++)
while (nf[j] != nf[nf[j]]) nf[j] = nf[nf[j]];
另一种情况是,我们可能能够构造一个布尔函数 equiv(j, k),当元素 与 相关时返回 true,否则返回 false。此时,我们需要遍历所有元素对以获得完整的关系图。D. Eardley 设计了一种巧妙的方法,在遍历所有元素对的同时,逐步将树向上压缩至高层祖先,从而保持树结构的最新状态,并省去了大部分最终的压缩步骤:
eclass.h
给定一个用户提供的布尔函数 equiv,用于判断范围在 内的任意两个元素是否相关,该函数在数组 nf[0..n-1] 中返回每个元素的等价类编号。
for (jj = 0; jj < n; jj++) {
nf[jj] = jj;
for (kk = 0; kk < jj; kk++) {
// 遍历所有元素对的第二个元素
nlf[kk] = nf[nf[kk]]; // 将其向上压缩至此程度
if (equiv(jj + 1, kk + 1)) nlf[nf[kk]] = jj;
// 读者可自行思考:为何需要压缩到此程度的祖先!
}
}
for (jj = 0; jj < n; jj++) nlf[jj] = nf[nf[jj]];
// 最终仅需进行如此程度的压缩
参考文献
Knuth, D.E. 1997, Fundamental Algorithms, 3rd ed., vol. 1 of The Art of Computer Programming (Reading, MA: Addison-Wesley), §2.3.3.[1]
Sedgewick, R. 1998, Algorithms in C, 3rd ed. (Reading, MA: Addison-Wesley), Chapter 30.