6.0 引言
所谓“特殊函数”并没有什么特别之处,只不过是有权威人士或教科书作者(这两者并不相同!)决定赋予它们这个名称而已。特殊函数有时也被称为高阶超越函数(比什么更高阶?),或数学物理函数(但它们也出现在其他领域),或满足某些常见二阶微分方程的函数(但并非所有特殊函数都如此)。或许我们干脆称它们为“有用函数”也就够了。本章所选包含哪些函数,具有高度的任意性。
市面上可获得的程序库中包含了许多特殊函数例程,这些例程面向的用户通常并不了解其内部实现机制。这类最先进的“黑箱”往往非常复杂,其中包含大量分支,会根据调用参数的值切换到完全不同的计算方法。黑箱例程(或至少应当)在所有参数范围内都具备严格的精度控制,达到所声明的统一精度。
在我们的示例中,我们不会如此苛求,部分原因是我们希望展示第5章中的技术,另一部分原因是我们希望你理解这些例程内部的工作原理。我们的一些例程包含一个精度参数,可以将其设得任意小;而另一些例程(尤其是涉及多项式拟合的)仅提供特定的精度,我们认为这种精度是可用的(通常,但并非总是,接近双精度)。我们并不保证这些例程是完美的黑箱。但我们希望,如果你在使用某个例程时遇到问题,能够根据我们提供的信息诊断并修正问题。
简而言之,本章的特殊函数例程是供实际使用的——我们自己就经常使用——但我们也希望你能从它们的内部实现中学到东西。
参考文献
Abramowitz, M., and Stegun, I.A. 1964, Handbook of Mathematical Functions (Washington: National Bureau of Standards); 1968年重印 (New York: Dover); 在线版见 http://www.nr.com/aands。
Andrews, G.E., Askey, R., and Roy, R. 1999, Special Functions (Cambridge, UK: Cambridge University Press)。
Thompson, W.J. 1997, Atlas for Computing Mathematical Functions (New York: Wiley-Interscience)。
Spanier, J., and Oldham, K.B. 1987, An Atlas of Functions (Washington: Hemisphere Pub. Corp.)。Wolfram, S. 2003, The Mathematica Book, 5th ed. (Champaign, IL: Wolfram Media)。
Hart, J.F., et al. 1968, Computer Approximations (New York: Wiley)。
Hastings, C. 1955, Approximations for Digital Computers (Princeton: Princeton University Press)。
Luke, Y.L. 1975, Mathematical Functions and Their Approximations (New York: Academic Press)。
6.1 伽马函数、贝塔函数、阶乘、二项式系数
伽马函数由如下积分定义:
当参数 为整数时,伽马函数就是我们熟悉的阶乘函数,但偏移了1:
伽马函数满足递推关系:
如果已知该函数在 或更一般地在复平面右半部 的值,则可通过反射公式得到 或 时的值:
注意, 在 及所有负整数处有极点。
目前有多种数值计算 的方法,但没有一种比 Lanczos [1] 推导出的近似公式更简洁。该方法专为伽马函数设计,看似凭空而来。我们不打算推导该近似公式,仅给出其最终形式:对于某些有理数 和整数 ,以及某些系数 ,伽马函数可表示为:
可以看出,这类似于斯特林(Stirling)近似,但增加了一系列修正项,以考虑复平面左侧的前几个极点。常数 非常接近于1。误差项由 参数化。当 ,并采用 P. Godfrey 计算的一组特定 系数和 值时,误差小于 。更令人印象深刻的是,使用相同的常数,公式 (6.1.5) 也适用于复伽马函数,在复平面右半部 的任意位置都几乎能达到实轴上同样的精度。
实现 比直接实现 更好,因为后者在 相对较小时就会发生溢出。伽马函数常用于计算中,其中 的大数值会被其他大数相除,结果是一个完全普通的数值。这类运算通常应编码为对数相减。有了公式 (6.1.5),我们只需调用两次对数函数并进行几十次算术运算,即可计算伽马函数的对数。这使得其实现难度并不比我们习以为常的其他内置函数(如 或 )高多少:
Doub gammln(const Doub xx) {
// 返回 ln[Γ(xx)] 的值,其中 xx > 0。
Int j;
Doub x, tmp, y, ser;
static const Doub cof[14] = {
57.1562356658629235, -59.5979603554754912,
14.1360979747417471, -0.491913816097620199,
0.339946499848118887e-4, 0.465236289270485756e-4,
-0.983744753048795646e-4, -0.158088703224912494e-3,
0.2102644441724104883e-3, -0.217439618115212643e-3,
-0.164318106536763890e-3, -0.844182239838527433e-4,
-0.261908384015814087e-4, -0.368991826595316234e-5
};
if (xx <= 0) throw("bad arg in gammln");
y = x = xx;
tmp = x + 5.24218750000000000;
tmp = (x + 0.5) * log(tmp) - tmp;
ser = 0.9999999999997092;
for (j = 0; j < 14; j++) ser += cof[j] / ++y;
return tmp + log(2.5066282746310005 * ser / x);
}
如何编写阶乘函数 的例程呢?通常阶乘函数用于较小的整数值,且在大多数应用中,相同的整数值会被多次调用。每次需要阶乘时都调用 显然是低效的。更好的做法是在首次调用时初始化一个静态表,后续调用则进行快速查找。表的固定大小为171,是因为 170! 可以用 IEEE 双精度浮点数表示,而 171! 会溢出。另外值得注意的是,22! 及以下的阶乘具有精确的双精度表示(尾数52位,不包括被指数吸收的2的幂次),而 23! 及以上则只能近似表示。
Doub factrl(const Int n) {
// gamma.h
// 返回阶乘 n! 的浮点数值。
static VecDoub a(171);
static Bool init = true;
if (init) {
init = false;
a[0] = 1.;
for (Int i = 1; i < 171; i++) a[i] = i * a[i-1];
}
if (n < 0 || n > 170) throw("factrl out of range");
return a[n];
}
在实际应用中,更有用的是返回阶乘对数的函数,因为它不会出现溢出问题。对数表的大小取决于你愿意在空间和初始化时间上付出多少代价。如果整数参数经常大于 2000,则应增大 NTOP = 2000 的值。
Doub factln(const Int n) {
// 返回 ln(n!)
static const Int NTOP = 2000;
static VecDoub a(NTOP);
static Bool init = true;
if (init) {
init = false;
for (Int i = 0; i < NTOP; i++) a[i] = gammln(i + 1);
}
if (n < 0) throw("negative arg in factln");
if (n < NTOP) return a[n];
return gammln(n + 1); // 超出表的范围。
}
二项式系数定义为:
下面的例程利用了 factrl 和 factln 中存储的表:
Doub bico(const Int n, const Int k) {
// 返回二项式系数 $\binom{n}{k}$ 的浮点数值。
if (n < 0 || k < 0 || k > n) throw("bad args in bico");
if (n < 171) return floor(0.5 + factrl(n) / (factrl(k) * factrl(n - k)));
return floor(0.5 + exp(factln(n) - factln(k) - factln(n - k)));
}
// floor 函数用于清除较小 n 和 k 值时的舍入误差。
如果你的问题需要一系列相关的二项式系数,一个好办法是使用递推关系,例如:
最后,我们离开整数参数的组合函数,转向 Beta 函数:
它与 Gamma 函数的关系为:
因此:
// gamma.h
Doub beta(const Doub z, const Doub w) {
// 返回 Beta 函数 $B(z,w)$ 的值。
return exp(gammln(z) + gammln(w) - gammln(z + w));
}
参考文献
Abramowitz, M., and Stegun, I.A. 1964, Handbook of Mathematical Functions (Washington: National Bureau of Standards); 1968 年重印 (New York: Dover); 在线版本见 http://www.nr.com/aands,第 6 章。
Lanczos, C. 1964, "A Precision Approximation of the Gamma Function," SIAM Journal on Numerical Analysis, ser. B, vol. 1, pp. 86–96.[1]
6.2 不完全 Gamma 函数与误差函数
不完全 Gamma 函数定义为:
其极限值为:
不完全 Gamma 函数 是单调的(当 大于约 1 时),在 位于 附近、宽度约为 的区间内,从“接近零”上升到“接近一”(见图 6.2.1)。
的补函数也令人困惑地被称为不完全 Gamma 函数:
其极限值为:
符号 、 和 是标准记号;而符号 是本书特有的。
有如下级数展开式:
实际上,并不需要对每个 都重新计算 ;而是利用公式 (6.1.3) 和前一个系数即可。
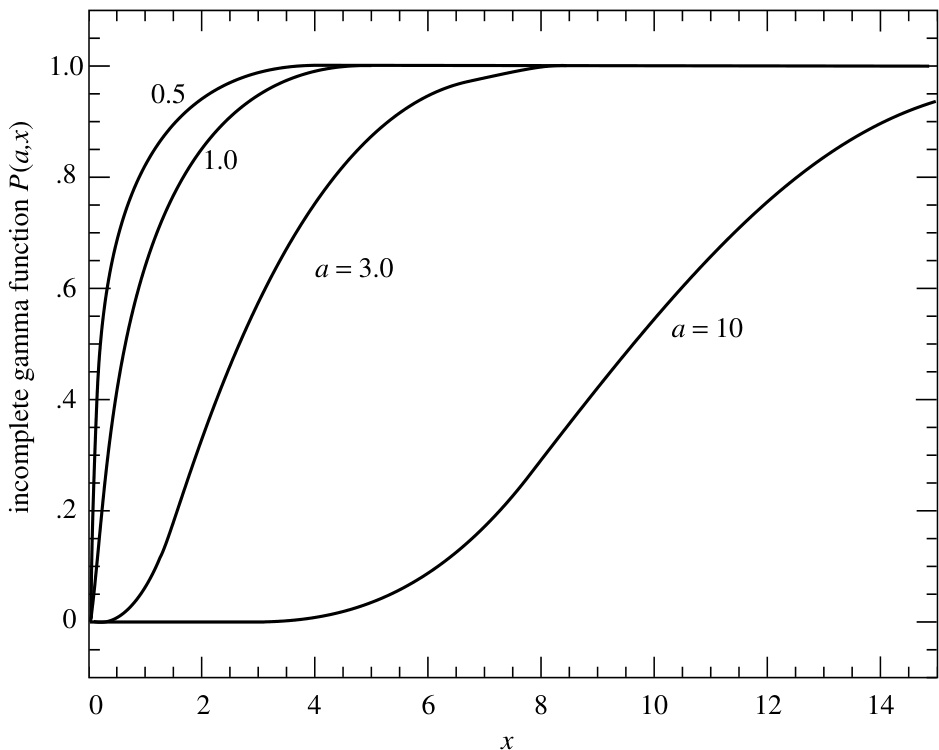
图 6.2.1. 不完全伽马函数 在四个不同 值下的图像。
有如下连分式展开式:
从计算角度看,使用 (6.2.6) 的偶数部分更好,其收敛速度提高了一倍(见 §5.2):
事实证明,当 小于约 时,(6.2.5) 快速收敛;而当 大于约 时,(6.2.6) 或 (6.2.7) 快速收敛。在各自适用的范围内,最多只需几倍于 项即可收敛,且仅在 附近(此时不完全伽马函数变化最快)才需要这么多项。对于中等大小的 (例如小于 100),结合使用 (6.2.5) 和 (6.2.7) 就足以计算所有 处的函数值。此外还有一个额外的好处:我们永远不需要通过两个几乎相等的数相减来计算接近零的函数值。
某些应用需要计算更大的 值下的 和 ,此时级数和连分式方法效率都很低。然而在此情形下,公式 (6.2.1) 中的被积函数在其峰值两侧迅速衰减,衰减范围仅为几倍 。一种高效的方法是直接计算该积分,采用单步高阶高斯-勒让德求积法(§4.6),积分区间从 延伸至最近的尾部,直到被积函数值可忽略为止。实际上这只是“半步”,因为我们只需要在 附近使用密集的横坐标点,而在尾部远处(被积函数已有效为零)则无需如此。
我们将各种不完全伽马函数部分封装到一个名为 Gamma 的对象中。其中唯一的持久状态是变量 ,它在最近一次调用 或 时被设为 。当你需要不同的归一化约定时(例如公式 (6.2.1) 或 (6.2.3) 中的 或 ),这个值会很有用。
struct Gamma : Gauleg18 {
// 不完全伽马函数的对象。Gauleg18 提供高斯-勒让德求积的系数。
static const Int ASWITCH = 100;
static const Doub EPS;
static const Doub FPMIN;
Doub gln;
Doub gammp(const Doub a, const Doub x) {
// 返回不完全伽马函数 $P(a,x)$。
if (x < 0.0 || a <= 0.0) throw("bad args in gammp");
if (x == 0.0) return 0.0;
else if ((Int)a >= ASWITCH) return gammpapprox(a, x, 1); // 求积法。
else if (x < a + 1.0) return gser(a, x); // 使用级数表示。
else return 1.0 - gcf(a, x); // 使用连分式表示。
}
Doub gammq(const Doub a, const Doub x) {
// 返回不完全伽马函数 $Q(a,x) \equiv 1 - P(a,x)$。
if (x < 0.0 || a <= 0.0) throw("bad args in gammp");
if (x == 0.0) return 1.0;
else if ((Int)a >= ASWITCH) return gammpapprox(a, x, 0); // 求积法。
else if (x < a + 1.0) return 1.0 - gser(a, x); // 使用级数表示。
else return gcf(a, x); // 使用连分式表示。
}
Doub gser(const Doub a, const Doub x) {
// 通过级数表示计算不完全伽马函数 $P(a,x)$。
// 同时将 ln $\Gamma(a)$ 存入 gln。用户不应直接调用。
Doub sum, del, ap;
gln = gammln(a);
ap = a;
del = sum = 1.0 / a;
for (;;) {
++ap;
del *= x / ap;
sum += del;
if (fabs(del) < fabs(sum) * EPS) {
return sum * exp(-x + a * log(x) - gln);
}
}
}
Doub gcf(const Doub a, const Doub x) {
// 通过连分式表示计算不完全伽马函数 $Q(a,x)$。
// 同时将 ln $\Gamma(a)$ 存入 gln。用户不应直接调用。
Int i;
Doub an, b, c, d, del, h;
gln = gammln(a);
b = x + 1.0 - a;
c = 1.0 / FPMIN;
d = 1.0 / b;
h = d;
for (i = 1;; i++) {
an = -i * (i - a);
b += 2.0;
d = an * d + b;
// 迭代至收敛。
if (fabs(d) < FPMIN) d = FPMIN;
c = b + an / c;
if (fabs(c) < FPMIN) c = FPMIN;
d = 1.0 / d;
del = d * c;
h *= del;
if (fabs(del - 1.0) <= EPS) break;
}
return exp(-x + a * log(x) - gln) * h; // 提取前置因子。
}
Doub gammpapprox(Doub a, Doub x, Int psig) {
// 通过数值积分计算不完全伽马函数。
// 当 psig 为 1 或 0 时,分别返回 $P(a,x)$ 或 $Q(a,x)$。
// 用户不应直接调用。
Int j;
Doub xu, t, sum, ans;
Doub a1 = a - 1.0, lna1 = log(a1), sqrta1 = sqrt(a1);
gln = gammln(a);
// 设置积分延伸到尾部的距离:
if (x > a1)
xu = MAX(a1 + 11.5 * sqrta1, x + 6.0 * sqrta1);
else
xu = MAX(0., MIN(a1 - 7.5 * sqrta1, x - 5.0 * sqrta1));
sum = 0;
for (j = 0; j < ngau; j++) {
t = x + (xu - x) * y[j];
sum += w[j] * exp(-(t - a1) + a1 * (log(t) - lna1));
}
ans = sum * (xu - x) * exp(a1 * (lna1 - 1.) - gln);
return (psig ? (ans > 0.0 ? 1.0 - ans : -ans) : (ans >= 0.0 ? ans : 1.0 + ans));
}
Doub invgammp(Doub p, Doub a);
// $P(a,x)$ 关于 $x$ 的反函数。见 §6.2.1。
};
const Doub Gamma::EPS = numeric_limits<Doub>::epsilon();
const Doub Gamma::FPMIN = numeric_limits<Doub>::min() / EPS;
请注意,由于 Gamma 是一个对象,必须先声明其实例才能使用其成员函数。我们习惯性地写成:
Gamma gam;
作为全局声明,然后根据需要调用 gam.gammp 或 gam.gammq。结构体 Gauleg18 仅包含高斯-勒让德求积的横坐标和权重。
struct Gauleg18 {
// 高斯-勒让德求积的横坐标和权重。
static const Int ngau = 18;
static const Doub y[18];
static const Doub w[18];
};
const Doub Gauleg18::y[18] = {
0.0021695375159141994,
0.011413521097787704, 0.027972308950302116, 0.051727015600492421,
0.082502225484340941, 0.12007019910960293, 0.16415283300752470,
0.21442376986779355, 0.27051082840644336, 0.33199876341447887,
0.39843234186401943, 0.46931971407375483, 0.54413605556657973,
0.62232745288031077, 0.70331500465597174, 0.78649910768313447,
0.87126389619061517, 0.95698180152629142
};
const Doub Gauleg18::w[18] = {
0.0055657196642445571,
0.012915947284065419, 0.020181515297735382, 0.027298621498568734,
0.034213810770299537, 0.040875750923643261, 0.047235083490265582,
0.053244713977759692, 0.058860144245324798, 0.064039797355015485,
0.068745323835736408, 0.072941885005653087, 0.076598410645870640,
0.079687828912071670, 0.082187266704339706, 0.084078218979661945,
0.085346685739338721, 0.085983275670394821
};
6.2.1 不完全伽马函数的反函数
在许多统计应用中,需要求不完全伽马函数的反函数,即对于给定的 ,求满足 的 值。若能给出足够好的初始猜测,牛顿法效果很好。事实上,这里非常适合使用 Halley 方法(见 §9.4),因为二阶导数(即被积函数的一阶导数)很容易计算。
对于 ,我们使用参考文献 [1] 中 §26.2.22 和 §26.4.17 给出的初始猜测。对于 ,我们首先粗略近似 :
然后在以下(粗略)近似式之一中求解 :
Doub Gamma::invgammp(Doub p, Doub a) {
// 返回满足 $P(a,x)=p$ 的 $x$,其中参数 $p$ 介于 0 和 1 之间。
Int j;
Doub x, err, t, u, pp, lna1, afac, a1 = a - 1;
const Doub EPS = 1.e-8;
gln = gammln(a);
if (a <= 0.) throw("a must be pos in invgammp");
if (p >= 1.) return MAX(100., a + 100. * sqrt(a));
if (p <= 0.) return 0.0;
if (a > 1.) {
lna1 = log(a1);
afac = exp(a1 * (lna1 - 1.) - gln);
pp = (p < 0.5) ? p : 1. - p;
t = sqrt(-2. * log(pp));
x = (2.30753 + t * 0.27061) / (1. + t * (0.99229 + t * 0.04481)) - t;
if (p < 0.5) x = -x;
x = MAX(1.e-3, a * pow(1. - 1. / (9. * a) - x / (3. * sqrt(a)), 3));
} else {
t = 1.0 - a * (0.253 + a * 0.12);
if (p < t)
x = pow(p / t, 1. / a);
else
x = 1. - (p - t) / (1. - t);
}
for (j = 0; j < 12; j++) {
if (x <= 0.0) return 0.0;
err = gammp(a, x) - p;
if (a > 1.)
t = afac * exp(-(x - a1) + a1 * (log(x) - lna1));
else
t = exp(-x + a1 * log(x) - gln);
u = err / t;
x -= (t = u / (1. - 0.5 * MIN(1., u * ((a - 1) / x - 1)))); // Halley 方法。
if (x <= 0.) x = 0.5 * (x + t);
if (fabs(t) < EPS * x) break;
}
return x;
}
6.2.2 误差函数
误差函数(error function)和互补误差函数(complementary error function)是不完全伽马函数的特例,可通过上述过程以适中的效率计算。它们的定义如下:
以及
这些函数具有以下极限值和对称性:
它们与不完全伽马函数的关系为:
以及
一种更快的计算方法利用如下形式的近似:
其中
而 是定义在 上的一个多项式,可通过切比雪夫方法(§5.8)求得。与伽马函数类似,其实现采用一个对象,该对象也包含反函数,此处同时包含 erf 和 erfc 的反函数。反函数的计算再次采用 Halley 方法(由 P.J. Acklam 提出)。
struct Erf {
// 用于误差函数及相关函数的对象。
static const Int ncof = 28;
static const Doub cof[28];
// 在结构体末尾进行初始化。
inline Doub erf(Doub x) {
// 对任意 x 返回 erf(x)。
if (x >= 0.) return 1.0 - erfccheb(x);
else return erfccheb(-x) - 1.0;
}
inline Doub erfc(Doub x) {
// 对任意 x 返回 erfc(x)。
if (x >= 0.) return erfccheb(x);
else return 2.0 - erfccheb(-x);
}
Doub erfccheb(Doub z) {
// 使用存储的切比雪夫系数计算公式 (6.2.16)。用户不应直接调用此函数。
Int j;
Doub t, ty, tmp, d = 0., dd = 0.;
if (z < 0.) throw("erfccheb requires nonnegative argument");
t = 2. / (2. + z);
ty = 4. * t - 2.;
for (j = ncof - 1; j > 0; j--) {
tmp = d;
d = ty * d - dd + cof[j];
dd = tmp;
}
return t * exp(-z * z + 0.5 * (cof[0] + ty * d) - dd);
}
Doub inverfc(Doub p) {
// 互补误差函数的反函数。返回 x,使得 erfc(x) = p,其中参数 p 介于 0 和 2 之间。
Doub x, err, t, pp;
if (p >= 2.0) return -100.;
if (p <= 0.0) return 100.;
pp = (p < 1.0) ? p : 2. - p;
t = sqrt(-2. * log(pp / 2));
x = -0.70711 * ((2.30753 + t * t * 0.27061) / (1. + t * (0.99229 + t * 0.04481)) - t);
for (Int j = 0; j < 2; j++) {
err = erfc(x) - pp;
x += err / (1.12837916709551257 * exp(-SQR(x)) - x * err); // Halley 方法。
}
return (p < 1.0 ? x : -x);
}
inline Doub inverf(Doub p) { return inverfc(1. - p); }
// 误差函数的反函数。返回 x,使得 erf(x) = p,其中参数 p 介于 -1 和 1 之间。
};
const Doub Erf::cof[28] = {
-1.3026537197817094, 6.4196979235649026e-1, 1.9476473204185836e-2, -9.561514786808631e-3,
-9.46595344482036e-4, 3.66839497852761e-4, 4.2523324806907e-5, -2.0278578112534e-5,
-1.624290004647e-6, 1.303655835580e-6, 1.5626441722e-8, -8.5238095915e-8,
6.529054439e-9, 5.059343495e-9, -9.91364156e-10, -2.27365122e-10,
9.6467911e-11, 2.394038e-12, -6.886027e-12, 8.94487e-13,
3.13092e-13, -1.12708e-13, 3.81e-16, 7.106e-15,
-1.523e-15, -9.4e-17, 1.21e-16, -2.8e-17
};
较低阶的切比雪夫近似可产生一个非常简洁的例程,尽管其精度仅约为单精度:
Doub erfcc(const Doub x)
// 返回互补误差函数 erfc(x),其相对误差处处小于 $1.2 \times 10^{-7}$。
{
Doub t, z = fabs(x), ans;
t = 2 / (2. + z);
ans = t * exp(-z * x - 1.26551223 + t * (1.00002368 + t * (0.37409196 + t * (0.09678418 +
t * (-0.18628806 + t * (0.27886807 + t * (-1.13520398 + t * (1.48851587 +
t * (-0.82215223 + t * (0.17087277)))))))));
return (x >= 0.0 ? ans : 2.0 - ans);
}
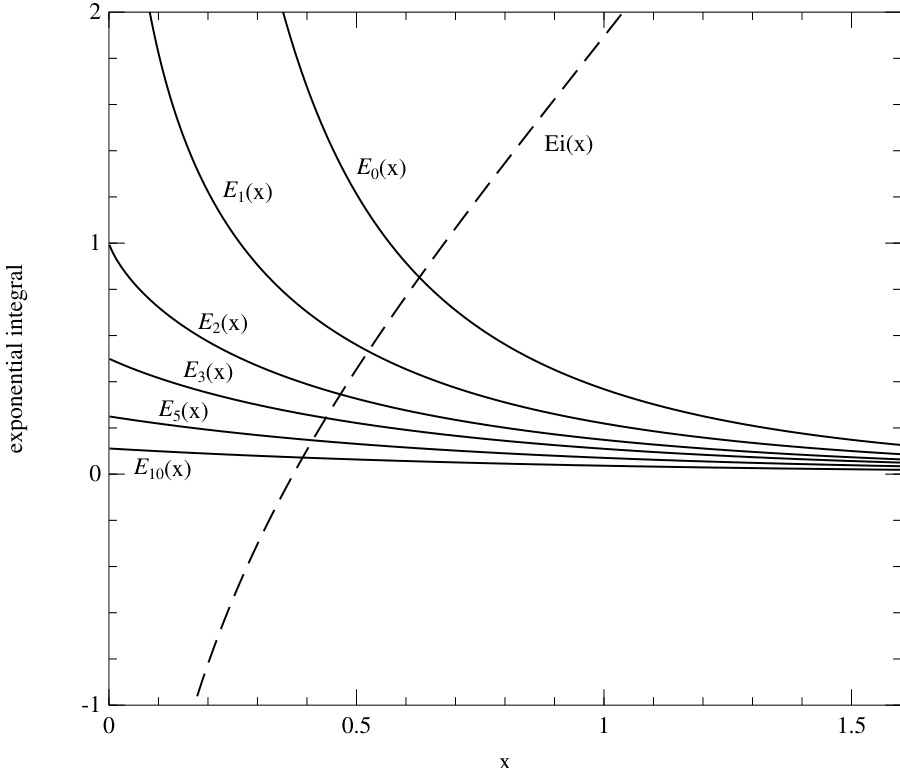
图 6.3.1. 指数积分 ( 和 )以及指数积分 。
参考文献
Abramowitz, M., and Stegun, I.A. 1964, Handbook of Mathematical Functions (Washington: National Bureau of Standards);1968 年重印版 (New York: Dover);在线版本见 http://www.nr.com/aands,第 6、7 和 26 章。[1]
Pearson, K. (ed.) 1951, Tables of the Incomplete Gamma Function (Cambridge, UK: Cambridge University Press)。
6.3 指数积分
指数积分的标准定义为
由如下积分主值定义的函数
也称为指数积分。注意, 通过解析延拓与 相关联。图 6.3.1 绘出了这些函数在典型参数值下的图像。
函数 是不完全伽马函数的一个特例:
因此,我们可以采用类似的策略对其进行计算。下面的连分式——即方程 (6.2.6) 的重写形式——对所有 均收敛:
我们采用其收敛更快的偶数形式:
该连分式仅在 时才真正足够快速地收敛以供实用。对于 ,我们可以使用级数表示:
此处 为双伽马函数(digamma function),对于整数参数,其定义为:
其中 为欧拉常数。我们按 的升幂顺序计算表达式 (6.3.6):
当 时,第一个方括号项被省略。这种计算方法的优点在于,对于较大的 ,级数在达到包含 的项之前就已收敛。因此,我们仅需对较小的 ()提供计算 的算法。我们采用公式 (6.3.7),尽管查表法可略微提高效率。
Amos [1] 对计算公式 (6.3.8) 时的截断误差进行了细致讨论,并给出了一种相当复杂的终止准则。我们发现,当最近加入的项小于所需容差时直接停止,效果几乎同样好。
两个特殊情况需单独处理:
例程 expint 可在机器浮点精度范围内,以任意精度 EPS 快速计算 。若需提高精度,唯一需要的修改是提供足够多位有效数字的欧拉常数。如有必要,Wrench [2] 可为你提供前 328 位数字!
Doub expint(const Int n, const Doub x)
// 计算指数积分 $E_{n}(x)$。
{
static const Int MAXIT = 100;
static const Doub Euler = 0.577215664901533,
EPS = numeric_limits<Doub>::epsilon(),
BIG = numeric_limits<Doub>::max() * EPS;
// MAXIT 为允许的最大迭代次数;
// Euler 为欧拉常数 γ;
// EPS 为期望的相对误差,不小于机器精度;
// BIG 为接近最大可表示浮点数的数值。
Int i, ii, nm1 = n - 1;
Doub a, b, c, d, del, fact, h, psi, ans;
if (n < 0 || x < 0.0 || (x == 0.0 && (n == 0 || n == 1)))
throw("bad arguments in expint");
if (n == 0) ans = exp(-x) / x;
else {
if (x == 0.0) ans = 1.0 / nm1;
else {
if (x > 1.0) {
b = x + n;
c = BIG;
d = 1.0 / b;
h = d;
for (i = 1; i <= MAXIT; i++) {
a = -i * (nm1 + i);
b += 2.0;
d = 1.0 / (a * d + b);
c = b + a / c;
del = c * d;
h *= del;
if (fabs(del - 1.0) <= EPS) {
ans = h * exp(-x);
return ans;
}
}
throw("continued fraction failed in expint");
} else {
// 计算级数。
ans = 0.0;
fact = 1.0;
for (i = 1; i <= MAXIT; i++) {
fact *= -x / i;
if (i != nm1)
del = -fact / (i - nm1);
else {
psi = -Euler;
for (ii = 1; ii <= nm1; ii++) psi += 1.0 / ii;
del = fact * (-log(x) + psi);
}
ans += del;
if (fabs(del) < fabs(ans) * EPS) return ans;
}
throw("series failed in expint");
}
}
}
return ans;
}
计算指数积分 的一个良好算法是:对小的 使用幂级数,对大的 使用渐近级数。幂级数为
其中 为欧拉常数。渐近展开式为
使用渐近展开式的下限大约为 ,其中 EPS 为所要求的相对误差。
Doub ei(const Doub x) {
// 计算指数积分 Ei(x),其中 x > 0。
static const Int MAXIT = 100;
static const Doub Euler = 0.577215664901533,
EPS = numeric_limits<Doub>::epsilon(),
FPMIN = numeric_limits<Doub>::min() / EPS;
其中,MAXIT 为允许的最大迭代次数;Euler 为欧拉常数 ;EPS 为相对误差(或在 零点 附近的绝对误差);FPMIN 为一个接近最小可表示浮点数的数值。
Int k;
Doub fact, prev, sum, term;
if (x <= 0.0) throw("Bad argument in ei");
if (x < FPMIN) return log(x) + Euler;
if (x <= -log(EPS)) {
sum = 0.0;
fact = 1.0;
for (k = 1; k <= MAXIT; k++) {
fact *= x / k;
term = fact / k;
sum += term;
if (term < EPS * sum) break;
}
if (k > MAXIT) throw("Series failed in ei");
return sum + log(x) + Euler;
} else {
sum = 0.0;
term = 1.0;
for (k = 1; k <= MAXIT; k++) {
prev = term;
term -= k / x;
if (term < EPS) break;
// 由于最终的和大于 1,term 本身近似为相对误差。
if (term < prev)
sum += term;
else {
sum -= prev;
break;
}
}
return exp(x) * (1.0 + sum) / x;
}
}
参考文献与延伸阅读:
Stegun, I.A., and Zucker, R. 1974, "Automatic Computing Methods for Special Functions. II. The Exponential Integral ," Journal of Research of the National Bureau of Standards, vol. 78B, pp. 199–216; 1976, “Automatic Computing Methods for Special Functions. III. The Sine, Cosine, Exponential Integrals, and Related Functions,” op. cit., vol. 80B, pp. 291–311.
Amos D.E. 1980, “Computation of Exponential Integrals,” ACM Transactions on Mathematical Software, vol. 6, pp. 365–377[1]; also vol. 6, pp. 420–428.
Abramowitz, M., and Stegun, I.A. 1964, Handbook of Mathematical Functions (Washington: National Bureau of Standards); reprinted 1968 (New York: Dover); online at http://www.nr.com/aands, Chapter 5.
Wrench J.W. 1952, “A New Calculation of Euler’s Constant,” Mathematical Tables and Other Aids to Computation, vol. 6, p. 255.[2]
6.4 不完全贝塔函数
不完全贝塔函数定义为
其极限值为
并满足对称关系
若 和 均远大于 1,则 在 附近会从“接近零”迅速上升至“接近一”。图 6.4.1 绘出了若干 对应的函数图像。
不完全贝塔函数具有如下级数展开式:
然而,该级数在数值计算中并不十分实用。(但请注意,系数中的贝塔函数可通过前一项值及少量乘法运算,利用公式 6.1.9 和 6.1.3 逐项计算。)
连分式表示则更为实用:
其中
当 时,该连分式快速收敛,除非 和 均很大,此时可能需要 次迭代。对于
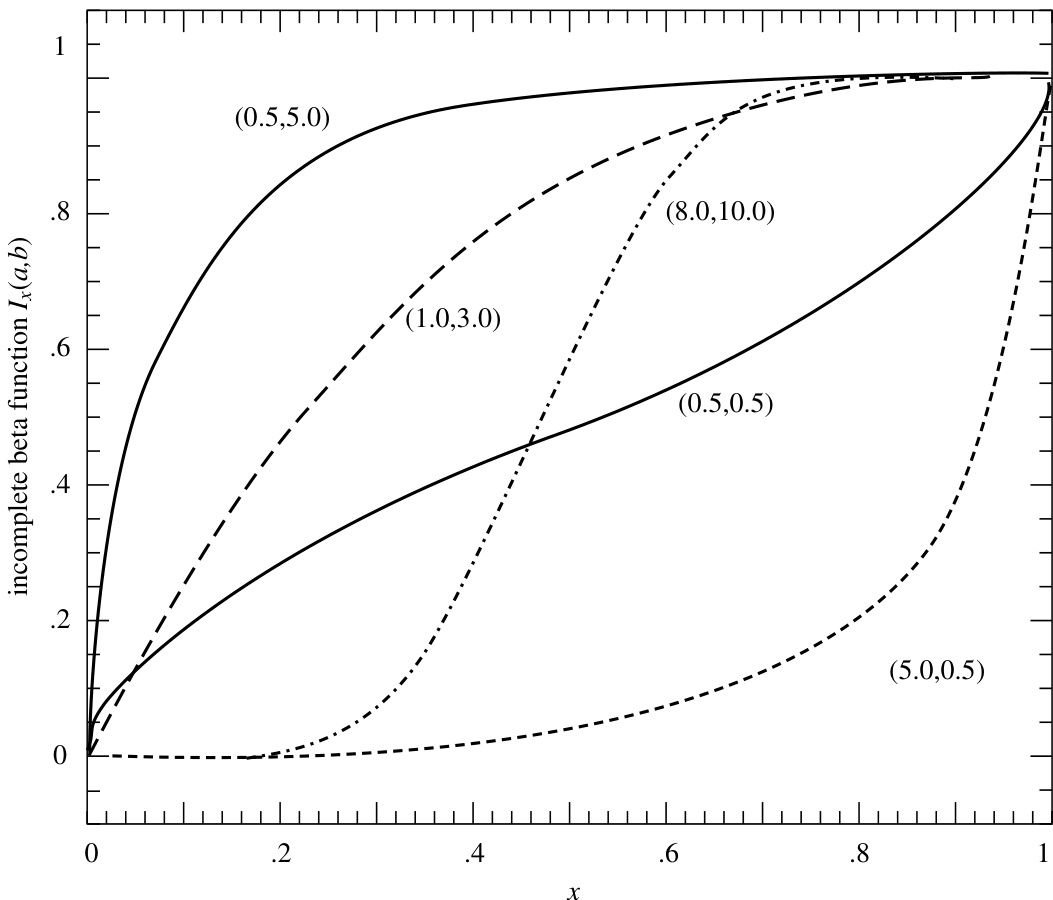
图 6.4.1. 不完全贝塔函数 对应五组不同的 值。注意, 和 这两组参数关于公式 (6.4.3) 所示的关系对称。
,我们可以直接利用对称关系 (6.4.3) 来获得一个等效的计算形式,从而再次实现快速收敛。因此,我们的计算策略与 Gamma 函数非常相似:通常使用连分式,但当 和 都很大时,则采用一次高阶高斯-勒让德(Gauss-Legendre)求积。
与 Gamma 函数类似,我们还使用 Halley 方法编写了一个反函数。当 和 都 时,初始猜测值来自参考文献 [1] 中的 §26.5.22。当其中任意一个小于 1 时,初始猜测值则来自对下式的一个粗略近似:
该近似通过在 处将积分拆分为两部分,并在每部分忽略被积函数中的一个因子得到。接着我们写出:
并在各自的区间内求解 。尽管这种近似较为粗糙,但在所有情况下都足以使初始值落在收敛域内。
struct Beta : Gauleg18 {
// 用于计算不完全贝塔函数的对象。Gauleg18 提供高斯-勒让德求积的系数。
static const Int SWITCH = 3000;
static const Doub EPS, FPMIN;
Doub betai(const Doub a, const Doub b, const Doub x) {
// 返回不完全贝塔函数 $I_{x}(a,b)$,其中 $a$ 和 $b$ 为正数,$x$ 介于 0 和 1 之间。
Doub bt;
if (a <= 0.0 || b <= 0.0) throw("Bad a or b in routine betai");
if (x < 0.0 || x > 1.0) throw("Bad x in routine betai");
if (x == 0.0 || x == 1.0) return x;
if (a > SWITCH && b > SWITCH) return betaiapprox(a, b, x);
bt = exp(gammln(a + b) - gammln(a) - gammln(b) + a * log(x) + b * log(1.0 - x));
if (x < (a + 1.0) / (a + b + 2.0))
return bt * betacf(a, b, x) / a;
else
return 1.0 - bt * betacf(b, a, 1.0 - x) / b;
}
Doub betacf(const Doub a, const Doub b, const Doub x) {
// 使用修正的 Lentz 方法(§5.2)计算不完全贝塔函数的连分式。用户不应直接调用。
Int m, m2;
Doub aa, c, d, del, h, qab, qam, qap;
qab = a + b;
qap = a + 1.0;
qam = a - 1.0;
c = 1.0;
d = 1.0 - qab * x / qap;
if (fabs(d) < FPMIN) d = FPMIN;
d = 1.0 / d;
h = d;
for (m = 1; m < 10000; m++) {
m2 = 2 * m;
aa = m * (b - m) * x / ((qam + m2) * (a + m2));
d = 1.0 + aa * d;
if (fabs(d) < FPMIN) d = FPMIN;
c = 1.0 + aa / c;
if (fabs(c) < FPMIN) c = FPMIN;
d = 1.0 / d;
h *= d * c;
aa = -(a + m) * (qab + m) * x / ((a + m2) * (qap + m2));
d = 1.0 + aa * d;
if (fabs(d) < FPMIN) d = FPMIN;
c = 1.0 + aa / c;
if (fabs(c) < FPMIN) c = FPMIN;
d = 1.0 / d;
del = d * c;
h *= del;
if (fabs(del - 1.0) <= EPS) break; // 完成了吗?
}
return h;
}
Doub betaiapprox(Doub a, Doub b, Doub x) {
// 通过数值积分计算不完全贝塔函数。返回 $I_{x}(a,b)$。用户不应直接调用。
Int j;
Doub xu, t, sum, ans;
Doub a1 = a - 1.0, b1 = b - 1.0, mu = a / (a + b);
Doub lnu = log(mu), lnnuc = log(1.0 - mu);
t = sqrt(a * b / (SQR(a + b) * (a + b + 1.0)));
if (x > a / (a + b)) {
if (x >= 1.0) return 1.0;
xu = MIN(1.0, MAX(mu + 10.0 * t, x + 5.0 * t));
} else {
if (x <= 0.0) return 0.0;
xu = MAX(0.0, MIN(mu - 10.0 * t, x - 5.0 * t));
}
sum = 0.0;
for (j = 0; j < 18; j++) {
t = x + (xu - x) * y[j];
sum += w[j] * exp(a1 * (log(t) - lnu) + b1 * (log(1.0 - t) - lnnuc));
}
ans = sum * (xu - x) * exp(a1 * (log(mu) - lnu) + b1 * (log(1.0 - mu) - lnnuc));
return ans > 0.0 ? 1.0 - ans : -ans;
}
Doub invbetai(Doub p, Doub a, Doub b) {
// 不完全贝塔函数的反函数。返回满足 $I_{x}(a,b) = p$ 的 $x$,其中 $p$ 介于 0 和 1 之间。
const Doub EPS = 1.e-8;
Doub pp, t, u, err, x, al, h, w, afac, a1 = a - 1.0, b1 = b - 1.0;
Int j;
if (p <= 0.0) return 0.0;
else if (p >= 1.0) return 1.0;
else if (a >= 1.0 && b >= 1.0) {
pp = (p < 0.5) ? p : 1.0 - p;
t = sqrt(-2.0 * log(pp));
x = (2.30753 + t * 0.27061) / (1.0 + t * (0.99229 + t * 0.04481)) - t;
if (p < 0.5) x = -x;
al = (SQR(x) - 3.0) / 6.0;
h = 2.0 / (1.0 / (2.0 * a - 1.0) + 1.0 / (2.0 * b - 1.0));
w = (x * sqrt(al + h) / h) - (1.0 / (2.0 * b - 1.0) - 1.0 / (2.0 * a - 1.0)) * (al + 5.0 / 6.0 - 2.0 / (3.0 * h));
x = a / (a + b * exp(2.0 * w));
} else {
Doub lna = log(a / (a + b)), lnb = log(b / (a + b));
t = exp(a * lna) / a;
u = exp(b * lnb) / b;
w = t + u;
if (p < t / w)
x = pow(a * w * p, 1.0 / a);
else
x = 1.0 - pow(b * w * (1.0 - p), 1.0 / b);
}
afac = -gammln(a) - gammln(b) + gammln(a + b);
for (j = 0; j < 10; j++) {
if (x == 0.0 || x == 1.0) return x;
err = betai(a, b, x) - p;
t = exp(a1 * log(x) + b1 * log(1.0 - x) + afac);
u = err / t;
x -= (t = u / (1.0 - 0.5 * MIN(1.0, u * (a1 / x - b1 / (1.0 - x)))));
if (x <= 0.0) x = 0.5 * (x + t);
if (x >= 1.0) x = 0.5 * (x + t + 1.0);
if (fabs(t) < EPS * x && j > 0) break;
}
return x;
}
const Doub Beta::EPS = numeric_limits<Doub>::epsilon();
const Doub Beta::FPMIN = numeric_limits<Doub>::min() / EPS;
};
参考文献
Abramowitz, M., and Stegun, I.A. 1964, Handbook of Mathematical Functions (Washington: National Bureau of Standards); 1968 年重印 (New York: Dover); 在线版本见 http://www.nr.com/aands,第 6 章和第 26 章。[1]
Pearson, E., and Johnson, N. 1968, Tables of the Incomplete Beta Function (Cambridge, UK: Cambridge University Press).
6.5 整数阶贝塞尔函数
本节介绍了计算各种整数阶贝塞尔函数的实用算法。在 §6.6 中我们将讨论分数阶的情况。实际上,适用于分数阶的更复杂算法同样可用于整数阶。但对于整数阶而言,本节中的算法更简单且更快。
对于任意实数 ,贝塞尔函数 可由如下级数定义:
该级数对所有 均收敛,但当 时计算效率不高。
当 不是整数时,贝塞尔函数 由下式给出:
当 趋近于某个整数 时,右边趋近于正确的极限值 ,但这种形式在计算上并不实用。
当 时,两类贝塞尔函数在定性上类似于简单的幂律函数,其在 时的渐近形式为:
当 时,两类贝塞尔函数在定性上类似于振幅按 衰减的正弦或余弦波。其在 时的渐近形式为:
在过渡区域 附近,贝塞尔函数的典型振幅量级为
该式在 很大时渐近成立。图 6.5.1 绘出了前几个各类贝塞尔函数。
贝塞尔函数满足递推关系:
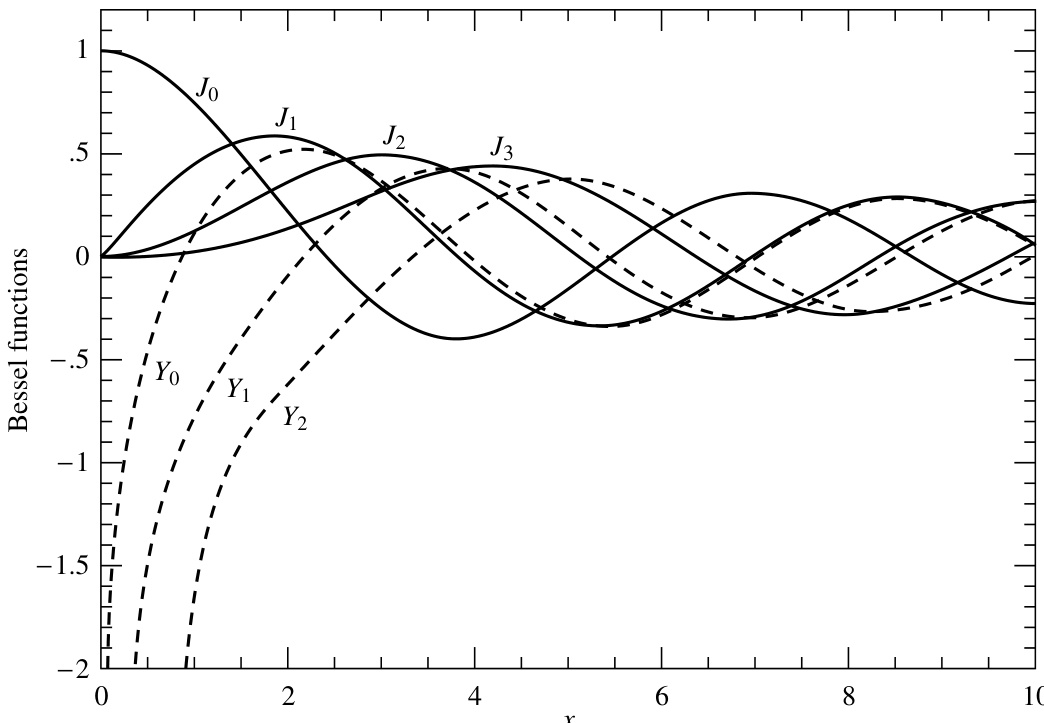
图 6.5.1. 贝塞尔函数 至 以及 至
以及
正如 §5.4 中已提到的,对于 ,只有后一个递推式(6.5.7)在 增加的方向上是稳定的。而(6.5.6)在 增加方向上不稳定的原因很简单:它与(6.5.7)是相同的递推关系;由舍入误差引入的微小“污染”项 会根据方程(6.5.3)迅速压倒所需的 。
计算整数阶贝塞尔函数的实用策略分为两个任务:第一,如何计算 、、 和 ;第二,如何稳定地利用递推关系求得其他 和 。我们先处理第一个任务。
对于 在零到某个任意值(我们取 8)之间的情形,用 的有理函数近似 和 。类似地,用有理函数近似 和 的“正则部分”,定义为
对于 ,使用如下近似形式():
其中
且 、、 和 均为其自变量的多项式,适用于 。其中 是偶多项式, 是奇多项式。
在下面的例程中,各种系数均以多精度计算,以确保相对误差达到完整的双精度。(在函数零点附近,绝对误差达到双精度。)然而,由于舍入误差,计算这些近似值可能导致最多损失两位有效数字。
还有一个额外的技巧:对于 的有理近似实际上以下列形式计算 [1]:
、 和 也类似处理。其中 和 是 在该区间内的两个零点, 和 是多项式。多项式 的系数符号交替变化。将其改写为关于 的形式可使所有系数符号相同,从而减少舍入误差。对于近似式(6.5.9)和(6.5.10),我们的系数与 Hart [2] 给出的类似但不完全相同。
函数 、、 和 共享大量代码,因此我们将它们封装为一个单一对象 Bessjy。用于计算更高阶 和 的例程也是其成员函数,具体实现将在下文讨论。所有数值系数均在 Bessjy 中声明,但定义(作为一长串常量)则单独给出;清单见 Webnote [3]。
// bessel.h
struct Bessjy {
static const Doub xj00, xj10, xj01, xj11, twoopi, pio4;
static const Doub j0r[7], j0s[7], j0pn[5], j0pd[5], j0qn[5], j0qd[5];
static const Doub j1r[7], j1s[7], j1pn[5], j1pd[5], j1qn[5], j1qd[5];
static const Doub y0r[9], y0s[9], y0pn[5], y0pd[5], y0qn[5], y0qd[5];
static const Doub y1r[8], y1s[8], y1pn[5], y1pd[5], y1qn[5], y1qd[5];
Doub nump, denp, numq, denq, y, z, ax, xx;
Doub j0(const Doub x) {
// 返回任意实数 x 的贝塞尔函数 $J_0(x)$。
if ((ax = abs(x)) < 8.0) {
// 直接有理函数拟合。
rat(x, j0r, j0s, 6);
return nump * (y - xj00) * (y - xj10) / denp;
} else {
asp(j0pn, j0pd, j0qn, j0qd, 1);
return sqrt(twoopi / ax) * (cos(xx) * nump / denp - z * sin(xx) * numq / denq);
}
}
Doub j1(const Doub x) {
// 返回任意实数 x 的贝塞尔函数 $J_1(x)$。
if ((ax = abs(x)) < 8.0) {
// 直接有理近似。
rat(x, j1r, j1s, 6);
return x * nump * (y - xj01) * (y - xj11) / denp;
} else {
asp(j1pn, j1pd, j1qn, j1qd, 3);
Doub ans = sqrt(twoopi / ax) * (cos(xx) * nump / denp - z * sin(xx) * numq / denq);
return ans;
}
}
Doub y0(const Doub x) {
// 返回正实数 x 的贝塞尔函数 $Y_0(x)$。
if (x < 8.0) {
Doub j0x = j0(x);
rat(x, y0r, y0s, 8);
return nump / denp + twoopi * j0x * log(x);
} else {
// 拟合函数 (6.5.10)。
ax = x;
asp(y0pn, y0pd, y0qn, y0qd, 1);
return sqrt(twoopi / x) * (sin(xx) * nump / denp + z * cos(xx) * numq / denq);
}
}
Doub y1(const Doub x) {
// 返回正实数 x 的贝塞尔函数 $Y_1(x)$。
if (x < 8.0) {
Doub j1x = j1(x);
rat(x, y1r, y1s, 7);
return x * nump / denp + twoopi * (j1x * log(x) - 1.0 / x);
} else {
ax = x;
asp(y1pn, y1pd, y1qn, y1qd, 3);
return sqrt(twoopi / x) * (sin(xx) * nump / denp + z * cos(xx) * numq / denq);
}
}
Doub jn(const Int n, const Doub x);
// 返回任意实数 x 和整数 n ≥ 0 的贝塞尔函数 $J_{n}(x)$。
Doub yn(const Int n, const Doub x);
// 返回任意正实数 x 和整数 n ≥ 0 的贝塞尔函数 $Y_{n}(x)$。
void rat(const Doub x, const Doub *r, const Doub *s, const Int n) {
// 公共代码:计算有理近似。
y = x * x;
z = 64.0 - y;
nump = r[n];
denp = s[n];
for (Int i = n - 1; i >= 0; i--) {
nump = nump * z + r[i];
denp = denp * y + s[i];
}
}
void asp(const Doub *pn, const Doub *pd, const Doub *qn, const Doub *qd,
const Doub fac) {
// 公共代码:计算渐近近似。
z = 8.0 / ax;
y = z * z;
xx = ax - fac * pio4;
nump = pn[4];
denp = pd[4];
numq = qn[4];
denq = qd[4];
for (Int i = 3; i >= 0; i--) {
nump = nump * y + pn[i];
denp = denp * y + pd[i];
numq = numq * y + qn[i];
denq = denq * y + qd[i];
}
}
};
我们现在转向第二个任务,即如何利用递推公式(6.5.6)和(6.5.7)计算 时的贝塞尔函数 和 。后者是直接的,因为其向上递推总是稳定的:
Doub Bessjy::yn(const Int n, const Doub x)
// 返回任意正实数 x 和整数 n ≥ 0 的贝塞尔函数 $Y_{n}(x)$。
{
Int j;
Doub by, bym, byp, tox;
if (n == 0) return y0(x);
if (n == 1) return y1(x);
tox = 2.0 / x;
by = y1(x);
bym = y0(x);
for (j = 1; j < n; j++) {
byp = j * tox * by - bym;
bym = by;
by = byp;
}
return by;
}
该算法的代价是调用 y1 和 y0(这会进一步调用 j1 和 j0),再加上递推中的 次运算。
对于 ,情况稍复杂一些。我们可以从 和 开始向上递推 ,但只有当 不超过 时,递推才是稳定的。然而,这对于大 和小 的调用已经足够好,而这种情况在实践中经常出现。
更难处理的情形是 。此时最佳做法是使用 Miller 算法(参见方程 5.4.16 前的讨论),从某个任意初始值开始向下递推,并利用该递推在向上方向的不稳定性,使我们回到正确的解。当我们最终到达 或 时,即可利用沿路累积的求和式(5.4.16)对解进行归一化。
唯一的微妙之处在于决定向下递推应从多大的 开始,才能在递推到我们真正需要的 时达到所需的精度。如果你研究一下渐近形式 (6.5.3) 和 (6.5.5),你应该能说服自己:答案是从比目标 大一个量级为 的值开始递推,其中该常数的平方根大致等于所需有效数字的位数。
上述考虑引出了以下函数。
jessel.h
Doub Bessjy::jn(const Int n, const Doub x)
// 返回贝塞尔函数 $J_{n}(x)$,适用于任意实数 x 和整数 n ≥ 0。
{
const Doub ACC = 160.0;
const Int IEXP = numeric_limits<Doub>::max_exponent / 2;
Bool jsum;
Int j, k, m;
Doub ax, bj, bjm, bjp, dum, sum, tox, ans;
if (n == 0) return j0(x);
if (n == 1) return j1(x);
ax = abs(x);
if (ax * ax <= 8.0 * numeric_limits<Doub>::min()) return 0.0;
else if (ax > Doub(n)) {
tox = 2.0 / ax;
// 从 $J_0$ 和 $J_1$ 向上递推。
bjm = j0(ax);
bj = j1(ax);
for (j = 1; j < n; j++) {
bjp = j * tox * bj - bjm;
bjm = bj;
bj = bjp;
}
ans = bj;
} else {
tox = 2.0 / ax;
m = 2 * ((n + Int(sqrt(ACC * n))) / 2);
jsum = false;
bjp = ans = sum = 0.0;
bj = 1.0;
for (j = m; j > 0; j--) {
bjm = j * tox * bj - bjp;
bjp = bj;
bj = bjm;
dum = frexp(bj, &k);
if (k > IEXP) {
bj = ldexp(bj, -IEXP);
bjp = ldexp(bjp, -IEXP);
ans = ldexp(ans, -IEXP);
sum = ldexp(sum, -IEXP);
}
if (jsum) sum += bj;
jsum = !jsum;
if (j == n) ans = bjp;
}
sum = 2.0 * sum - bj;
ans /= sum;
}
return x < 0.0 && (n & 1) ? -ans : ans;
}
上面使用的函数 ldexp 是 C 和 C++ 标准库中的函数,用于调整一个数的二进制指数。
6.5.1 整数阶修正贝塞尔函数
修正贝塞尔函数 和 等价于通常的贝塞尔函数 和 在纯虚数自变量下的取值。具体关系为:
选择特定的前置因子以及 和 的特定线性组合来构造 ,只是为了使这些函数在实数自变量 下取实数值。
对于小自变量 , 和 的渐近行为都是其自变量的简单幂函数:
这些表达式与该区域中 和 的表达式几乎完全相同,只是 与 之间相差一个因子 。然而,在区域 中,修正贝塞尔函数的行为与普通贝塞尔函数截然不同:
显然,修正贝塞尔函数在大自变量下呈指数行为而非正弦振荡行为(见图 6.5.2)。类似于 和 贝塞尔函数的有理逼近方法,也可高效地用于计算 、、 和 。相应的例程被封装在一个名为 Bessik 的对象中。这些例程与文献 [1] 中的类似,但在细节上有所不同。(所有常数同样列在 Webnote [3] 中。)
struct Bessik {
static const Doub i0p[14], i0q[5], i0pp[5], i0qq[6];
static const Doub i1p[14], i1q[5], i1pp[5], i1qq[6];
static const Doub k0pi[5], k0qi[3], k0p[5], k0q[3], k0pp[8], k0qq[8];
static const Doub k1pi[5], k1qi[3], k1p[5], k1q[3], k1pp[8], k1qq[8];
Doub y, z, ax, term;
Doub i0(const Doub x) {
// 返回修正贝塞尔函数 $I_0(x)$,适用于任意实数 x。
if ((ax = abs(x)) < 15.0) {
// 有理逼近。
y = x * x;
return poly(i0p, 13, y) / poly(i0q, 4, 225.0 - y);
} else {
z = 1.0 - 15.0 / ax;
return exp(ax) * poly(i0pp, 4, z) / (poly(i0qq, 5, z) * sqrt(ax));
}
}
Doub i1(const Doub x) {
// 返回修正贝塞尔函数 $I_1(x)$,适用于任意实数 x。
if ((ax = abs(x)) < 15.0) {
// 有理逼近。
y = x * x;
return x * poly(i1p, 13, y) / poly(i1q, 4, 225.0 - y);
} else {
// 提取因子 $e^x/\sqrt{x}$ 的有理逼近。
z = 1.0 - 15.0 / ax;
Doub ans = exp(ax) * poly(i1pp, 4, z) / (poly(i1qq, 5, z) * sqrt(ax));
return x > 0.0 ? ans : -ans;
}
}
Doub k0(const Doub x) {
// 返回修正贝塞尔函数 $K_0(x)$,适用于正实数 x。
if (x <= 1.0) {
z = x * x;
term = poly(k0pi, 4, z) * log(x) / poly(k0qi, 2, 1.0 - z);
return poly(k0p, 4, z) / poly(k0q, 2, 1.0 - z) - term;
} else {
z = 1.0 / x;
return exp(-x) * poly(k0pp, 7, z) / (poly(k0qq, 7, z) * sqrt(x));
}
}
};
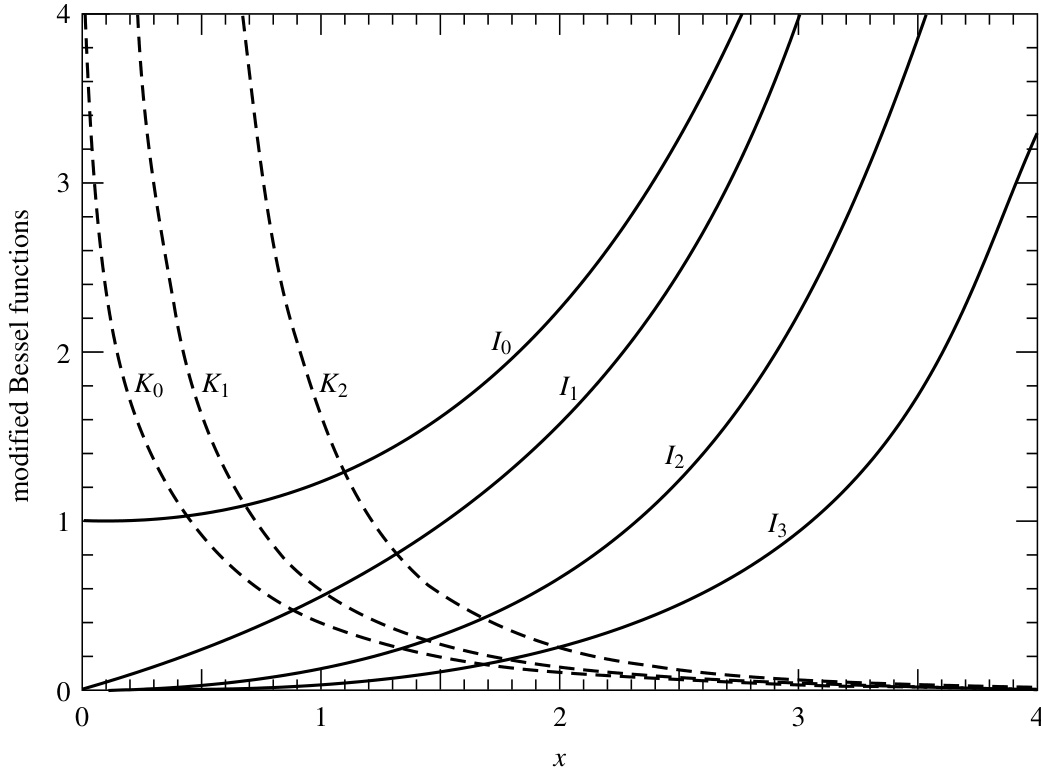
图 6.5.2. 修正贝塞尔函数 到 ,以及 到 。
Doub k1(const Doub x) {
// 返回修正贝塞尔函数 $K_1(x)$,适用于正实数 x。
if (x <= 1.0) {
z = x * x;
term = poly(k1pi, 4, z) * log(x) / poly(k1qi, 2, 1.0 - z);
return x * (poly(k1p, 4, z) / poly(k1q, 2, 1.0 - z) + term) + 1.0 / x;
} else {
// 提取因子 $e^{-x}/\sqrt{x}$ 的有理逼近。
z = 1.0 / x;
return exp(-x) * poly(k1pp, 7, z) / (poly(k1qq, 7, z) * sqrt(x));
}
}
Doub in(const Int n, const Doub x);
// 返回修正贝塞尔函数 $I_n(x)$,适用于任意实数 x 和 n ≥ 0。
Doub kn(const Int n, const Doub x);
// 返回修正贝塞尔函数 $K_n(x)$,适用于正实数 x 和 n ≥ 0。
Doub poly(const Doub *cof, const Int n, const Doub x) {
// 通用代码:计算多项式。
Doub ans = cof[n];
for (Int i = n - 1; i >= 0; i--) ans = ans * x + cof[i];
return ans;
}
和 的递推关系与 和 的相同,只需将 替换为 。这会导致递推关系中符号的变化:
这些关系在向上递推时总是不稳定的。对于本身递增的 ,这不会造成问题。其实现如下:
Doub Bessik::kn(const Int n, const Doub x)
// 返回修正贝塞尔函数 $K_n(x)$,适用于正实数 x 和 n ≥ 0。
{
Int j;
Doub bk, bkm, bkp, tox;
if (n == 0) return k0(x);
if (n == 1) return k1(x);
tox = 2.0 / x;
bkm = k0(x);
bk = k1(x);
for (j = 1; j < n; j++) {
// 这里就是递推公式。
bkp = bkm + j * tox * bk;
bkm = bk;
bk = bkp;
}
return bk;
}
对于 ,仍需采用向下递推策略,且递推起点的选择方式与 Bessjy::jn 例程相同。唯一的根本区别在于 的归一化公式中,各项符号交替变化,这同样源于将之前用于 的公式中的 替换为 :
实际上,我们更倾向于直接通过调用 i0 来进行归一化。
bessel.h Doub Bessik::in(const Int n, const Doub x)
返回修正贝塞尔函数 ,适用于任意实数 且 。
{
const Doub ACC=200.0;
const Int IEXP=numeric_limits
Int j,k;
Doub bi,bim,bip,dum,tox,ans;
if (n==0) return i0(x);
if (n==1) return i1(x);
if (xx <= 8.0numeric_limits
else {
tox=2.0/abs(x);
bip=ans=0.0;
bi=1.0;
for (j=2*(n+Int(sqrt(ACCn))));j>0;j--) {
bim=bip+jtox*bi;
bip=bi;
bi=bim;
dum=frexp(bi,&k);
if (k > IEXP) {
ans=ldexp(ans,-IEXP);
bi=ldexp(bi,-IEXP);
bip=ldexp(bip,-IEXP);
}
} // 重新归一化以防止溢出。
}
if (j == n) ans=bip;
ans *= i0(x)/bi;
return x < 0.0 && (n & 1) ? -ans : ans;
}
上面使用的函数 ldexp 是 C 和 C++ 标准库中用于调整数值二进制指数的函数。
参考文献
Abramowitz, M., and Stegun, I.A. 1964, Handbook of Mathematical Functions (Washington: National Bureau of Standards); 1968 年重印 (New York: Dover); 在线版见 http://www.nr.com/aands,第 9 章。
Carrier, G.F., Krook, M. and Pearson, C.E. 1966, Functions of a Complex Variable (New York: McGraw-Hill), 第 220 页及以后。
SPECFUN, 2007+, 见 http://www.netlib.org/specfun.[1]
Hart, J.F., et al. 1968, Computer Approximations (New York: Wiley), §6.8, 第 141 页。[2]
Numerical Recipes Software 2007, "Coefficients Used in the Bessjy and Bessik Objects," Numerical Recipes Webnote No. 7, 见 http://www.nr.com/webnotes?7 [3]
6.6 分数阶贝塞尔函数、艾里函数、球贝塞尔函数
已经提出了许多用于数值计算分数阶贝塞尔函数的算法。事实上,其中大多数在实践中效果并不理想。此处给出的例程相当复杂,但可以强烈推荐使用。
6.6.1 普通贝塞尔函数
基本思想是 Steed 方法,该方法最初是为库仑波函数开发的 [1]。该方法同时计算 、、 和 ,因此涉及这四个函数之间的四种关系。其中三种关系来自两个连分式,其中之一是复数形式。第四种关系由朗斯基行列式(Wronskian)给出:
第一个连分式 CF1 定义为:
你可以很容易地从贝塞尔函数的三项递推关系推导出它:从方程 (6.5.6) 出发,并使用方程 (5.4.18)。通过 §5.2 中的方法之一对连分式进行前向求值,本质上等价于递推关系的后向递推。CF1 的收敛速率由转折点 的位置决定,超过该点后贝塞尔函数变为振荡形式。若 ,
收敛非常迅速。若 ,则连分式的每次迭代实际上将 增加 1,直到 ;此后便迅速收敛。因此,对于大的 ,CF1 的迭代次数约为 的量级。在例程 besseljy 中,我们将允许的最大迭代次数设为 10,000。对于更大的 ,你可以使用贝塞尔函数的标准渐近表达式。
可以证明,一旦 CF1 收敛, 的符号就与 CF1 分母的符号相同。
复连分式 CF2 定义为:
(我们在下一小节中简要推导修正贝塞尔函数情形下 CF2 的类似形式。)该连分式在 时快速收敛,但在 时失效。对于小 ,我们必须采用一种特殊方法,如下所述。当 不太小时,我们可以通过对 和 进行稳定递推,向下递推至某个 ,从而得到该较低 值处的比值 。这是递推关系的稳定方向。递推的初始值为:
其中 的任意初始值的符号选择为 CF1 分母的符号。将 的初始值选得非常小,可以最小化递推过程中发生溢出的可能性。递推关系为:
一旦在 处求得 CF2,再结合朗斯基行列式 (6.6.1),我们便有足够的关系式来求解全部四个量。通过引入量
可简化公式。于是有:
式 (6.6.7) 中 的符号选择为与式 (6.6.4) 中初始 的符号相同。
一旦在 处确定了全部四个函数,我们就可以求出它们在原始 值处的值。对于 和 ,只需将式 (6.6.4) 中的值按式 (6.6.7) 与应用递推关系 (6.6.5) 后所得值的比值进行缩放即可。量 和 可通过从式 (6.6.9) 和 (6.6.10) 的值出发,利用稳定的向上递推公式
以及关系式
来求得。
现在考虑 较小、CF2 方法不适用的情形。Temme [2] 给出了一种通过级数展开计算 和 (进而由式 (6.6.12) 得到 )的良好方法,该方法能准确处理 时的奇异性。这些展开式仅适用于 ,因此现在利用递推式 (6.6.5) 将 计算到该区间内的某个 值。然后通过下式计算 :
并由式 (6.6.8) 计算 。原始 值处的函数值仍通过前述缩放方法确定,而 函数则如前所述向上递推得到。
Temme 的级数为
其中
而系数 和 由可通过递推计算的量 、 和 定义:
递推的初始值为
其中
以这种方式书写公式的目的在于,当 时可能出现的问题可以通过仔细计算 、 和 来加以控制。特别地,Temme 给出了 和 的切比雪夫展开式。我们按照 §5.8 中所述,将他给出的 展开式重新整理为显式的关于 的偶次幂级数,以提高计算效率。
由于 、、 和 是同时计算的,因此一个无返回值的函数即可一次性设置所有这些值。用户随后可直接从对象中提取所需的结果。或者,也可以使用函数 jnu 和 ynu。(我们省略了类似的导数辅助函数,但你可以轻松地自行添加。)对象 Bessel 还包含其他将在下文讨论的方法。
这些例程假设 。对于负的 ,可使用反射公式:
例程还假设 。对于 ,函数一般为复数,但可用 的函数表示。对于 , 是奇异的。复数运算通过实变量显式完成。
struct Bessel {
static const Int NUSE1 = 7, NUSE2 = 8;
static const Doub c1[NUSE1], c2[NUSE2];
Doub xo, nuo;
Doub jo, yo, jpo, ypo;
Doub io, ko, ipo, kpo;
Doub ai, bio, ipo;
Doub sphjo, sphyo, sphjpo, sphypo;
Int sphno;
Bessel() : xo(9.99e99), nuo(9.99e99), sphno(-9999) {}
// 默认构造函数,无参数。
void besseljy(const Doub nu, const Doub x);
// 计算贝塞尔函数 $J_{\nu}(x)$ 和 $Y_{\nu}(x)$ 及其导数。
void besseljk(const Doub nu, const Doub x);
// 计算贝塞尔函数 $I_{\nu}(x)$ 和 $K_{\nu}(x)$ 及其导数。
Doub jnu(const Doub nu, const Doub x) {
if (nu != nuo || x != xo) besseljy(nu, x);
return jo;
}
Doub ynu(const Doub nu, const Doub x) {
// 简单接口,返回 $Y_{\nu}(x)$。
if (nu != nuo || x != xo) besseljy(nu, x);
return yo;
}
Doub inu(const Doub nu, const Doub x) {
// 简单接口,返回 $I_{\nu}(x)$。
if (nu != nuo || x != xo) besseljk(nu, x);
return io;
}
Doub knu(const Doub nu, const Doub x) {
// 简单接口,返回 $K_{\nu}(x)$。
if (nu != nuo || x != xo) besseljk(nu, x);
return ko;
}
void airy(const Doub x);
// 计算艾里函数 Ai(x) 和 Bi(x) 及其导数。
Doub airy_ai(const Doub x);
// 简单接口,返回 Ai(x)。
Doub airy_bi(const Doub x);
// 简单接口,返回 Bi(x)。
};
void sphbes(const Int n, const Doub x);
// 计算球贝塞尔函数 $j_{n}(x)$ 和 $y_{n}(x)$ 及其导数。
Doub sphbesj(const Int n, const Doub x);
// 简单接口,返回 $j_{n}(x)$。
Doub sphbesy(const Int n, const Doub x);
// 简单接口,返回 $y_{n}(x)$。
inline Doub chebev(const Doub *c, const Int m, const Doub x) {
// 由 besseljy 和 bessellik 使用的工具函数,用于计算切比雪夫级数。
Doub d = 0.0, dd = 0.0, sv;
Int j;
for (j = m - 1; j > 0; j--) {
sv = d;
d = 2. * x * d - dd + c[j];
dd = sv;
}
return x * d - dd + 0.5 * c[0];
}
const Doub Bessel::c1[7] = {
-1.142022680371168e0, 6.5165112670737e-3, 3.087090173086e-4,
-3.4706269649e-6, 6.9437664e-9, 3.67795e-11, -1.356e-13
};
const Doub Bessel::c2[8] = {
1.843740587300905e0, -7.68528408447867e-2, 1.2719271366546e-3,
-4.9717367042e-6, -3.31261198e-8, 2.423096e-10,
-1.702e-13, -1.49e-15
};
Bessel::besseljy 的代码清单见网络附注 [4]。
6.6.2 修正贝塞尔函数
Steed 方法不适用于修正贝塞尔函数,因为在这种情况下,CF2 是纯虚数,且四个函数之间仅有三个关系式。Temme [3] 给出了一个归一化条件,提供了第四个关系式。
朗斯基行列式关系为:
连分式 CF1 变为:
为了以方便的形式得到 CF2 和归一化条件,考虑如下合流超几何函数序列:
其中 固定。则有:
式 (6.6.23) 是用合流超几何函数表示 的标准表达式,而式 (6.6.24) 则由相邻合流超几何函数之间的关系导出(参见文献 [5] 中的公式 13.4.16 和 13.4.18)。函数 满足三项递推关系(参见文献 [5] 中的公式 13.4.15):
其中:
按照推导式 (5.4.18) 的步骤,可得连分式 CF2:
由此,通过式 (6.6.24) 可得 ,进而得到 。
Temme 的归一化条件为:
其中:
注意,系数 可通过递推关系确定:
我们通过计算下式来应用条件 (6.6.28):
于是
而式 (6.6.23) 给出了 。
Thompson 和 Barnett [6] 提出了一种巧妙的方法,可以在前向计算连分式 CF2 的同时完成求和 (6.6.31)。假设连分式按如下方式计算:
其中增量 可通过例如 Steed 算法或 §5.2 中所述的改进 Lentz 算法求得。那么保留前 项对 的近似值可表示为
这里
而 可通过递推关系
求得,初始条件为 ,。在当前情形下,要使 收敛所需的项数大约是仅使 CF2 收敛所需项数的三倍。
对于小 的情形,我们使用类似于 (6.6.14) 的级数来计算 和 :
其中
递推的初始值为
对于小 的级数以及 CF2 和归一化关系 (6.6.28),均要求 。因此在这两种情形下,我们都将 递推至该区间内的某个值 ,在此处计算 ,然后再将 递推回原始的 值。
该例程假设 。对于负的 ,需使用反射公式:
注意,当 很大时, 而 ,因此这些函数可能发生溢出或下溢。通常我们希望计算缩放后的量 和 。只需在式 (6.6.23) 中省略因子 ,即可保证所有四个量具有适当的缩放。如果你还想在使用式 (6.6.37) 中的级数计算小 情形时对这四个量进行缩放,则必须将每个级数乘以 。
与 besseljy 类似,你可以调用无返回值的函数 besselik,然后从对象中获取函数值和/或导数值;或者直接调用 inu 或 knu。
Bessel::besselik 的代码清单见 Webnote [4]。
6.6.3 Airy 函数
对于正的 ,Airy 函数定义为
其中
利用反射公式(6.6.40),我们可以将(6.6.42)转换为计算上更有用的形式:
这样,Ai 和 Bi 就可以通过一次对 besselik 的调用进行计算。
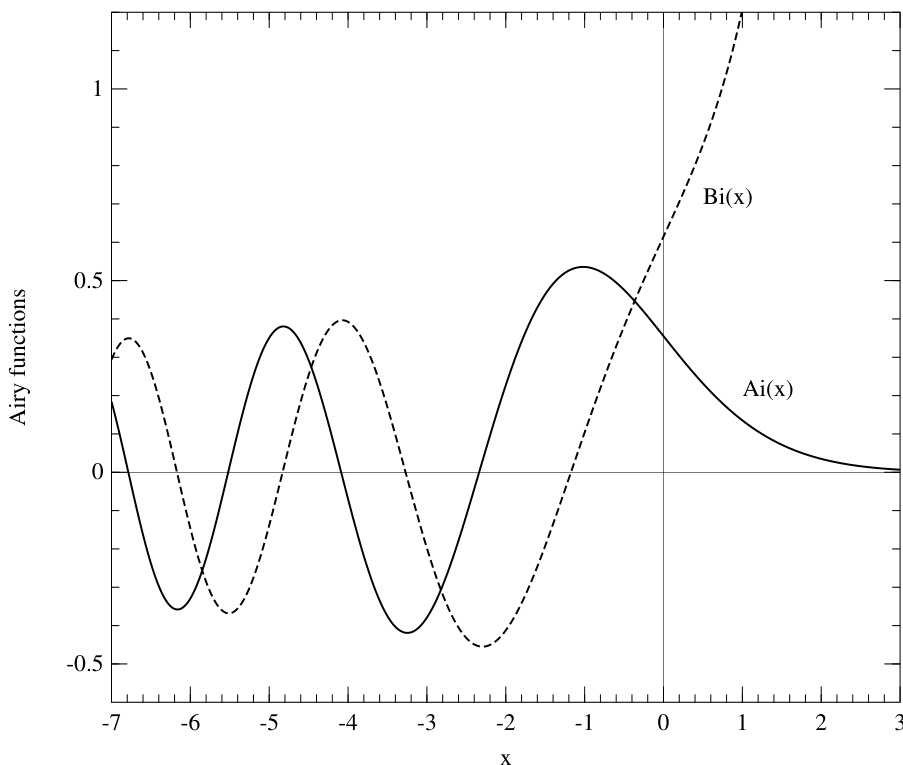
图 6.6.1. 艾里函数 和 。
由于在 附近直接对上述表达式求导可能导致相减误差,因此不应简单地通过微分这些表达式来计算导数。应改用以下等价表达式:
对于负自变量,相应的公式为:
besselfrac.h
if (x > 0.0) {
besselik(THR,z);
ai = rootx*ONOVRT*ko/PI;
bio = rootx*(ko/PI+2.0*ONOVRT*io);
besselik(TWOTHER,z);
aipo = -x*ONOVRT*ko/PI;
bipo = x*(ko/PI+2.0*ONOVRT*io);
} else if (x < 0.0) {
besseljy(THR,z);
ai = 0.5*rootx*(jo-ONOVRT*yvo);
bio = -0.5*rootx*(yo+ONOVRT*yvo);
besseljy(TWOTHER,z);
aipo = 0.5*absx*(ONOVRT*yot+jo);
bipo = 0.5*absx*(ONOVRT*yot-yo);
} else {
aio=0.355028053887817;
bio=aio/ONOVRT;
aipo = -0.258819403792807;
bipo = -aipo/ONOVRT;
}
Doub Bessel::airy_ai(const Doub x) {
// Simple interface returning Ai(x).
if (x != xo) airy(x);
return aio;
}
Doub Bessel::airy_bi(const Doub x) {
// Simple interface returning Bi(x).
if (x != xo) airy(x);
return bio;
}
6.6.4 球贝塞尔函数
对于整数 ,球贝塞尔函数定义为:
它们可以通过调用 besseljy 进行计算,其导数也可以安全地通过公式(6.6.47)的导数求得。
注意,在(6.6.3)中的连分式 CF2 中,当 时,仅第一项保留。因此,可以沿用 besseljy 的思路,构造一个非常简单的球贝塞尔函数算法:始终将 递推至 ,从 CF2 的第一项设定 和 ,然后向上递推 。在 附近无需特殊级数展开。然而,besseljy 已经非常高效,因此我们并未提供独立的球贝塞尔函数例程。
void Bessel::sphbes(const Int n, const Doub x) {
// Sets sphjo, sphyo, sphjpo, and sphypo, respectively, to the spherical Bessel functions
// $j_{n}(x)$, $y_{n}(x)$, and their derivatives $j_{n}^{\prime}(x)$, $y_{n}^{\prime}(x)$
// for integer n (which is saved as sphno).
const Doub RTPI02=1.253314137315500251;
Doub factor, order;
if (n < 0 || x <= 0.0) throw("bad arguments in sphbes");
order = n + 0.5;
besseljy(order, x);
factor = RTPI02 / sqrt(x);
sphjo = factor * jo;
sphyo = factor * yo;
sphjpo = factor * jpo - sphjo / (2.0 * x);
sphypo = factor * ypo - sphyo / (2.0 * x);
sphno = n;
}
Doub Bessel::sphbesj(const Int n, const Doub x) {
// Simple interface returning $j_{n}(x)$.
if (n != sphno || x != xo) sphbes(n, x);
return sphjo;
}
Doub Bessel::sphbesy(const Int n, const Doub x) {
// Simple interface returning $y_{n}(x)$.
if (n != sphno || x != xo) sphbes(n, x);
return sphyo;
}
参考文献
Barnett, A.R., Feng, D.H., Steed, J.W., and Goldfarb, L.J.B. 1974, "Coulomb Wave Functions for All Real and ", Computer Physics Communications, vol. 8, pp. 377–395.[1]
Temme, N.M. 1976, "On the Numerical Evaluation of the Ordinary Bessel Function of the Second Kind," Journal of Computational Physics, vol. 21, pp. 343–350[2]; 1975, op. cit., vol. 19, pp. 324–337.[3]
Numerical Recipes Software 2007, "Bessel Function Implementations," Numerical Recipes Webnote No. 8, at http://www.nr.com/webnotes?8 [4]
Abramowitz, M., and Stegun, I.A. 1964, Handbook of Mathematical Functions (Washington: National Bureau of Standards); reprinted 1968 (New York: Dover); online at http://www.nr.com/aands, Chapter 10.[5]
Thompson, I.J., and Barnett, A.R. 1987, "Modified Bessel Functions and of Real Order and Complex Argument, to Selected Accuracy," Computer Physics Communications, vol. 47, pp. 245–257.[6]
Barnett, A.R. 1981, "An Algorithm for Regular and Irregular Coulomb and Bessel functions of Real Order to Machine Accuracy," Computer Physics Communications, vol. 21, pp. 297–314.
Thompson, I.J., and Barnett, A.R. 1986, "Coulomb and Bessel Functions of Complex Arguments and Order," Journal of Computational Physics, vol. 64, pp. 490–509.
6.7 球谐函数
球谐函数出现在大量物理问题中,例如,当在球坐标系下通过分离变量法求解波动方程或拉普拉斯方程时。球谐函数 (其中 )是球面上两个坐标 的函数。
不同 和 的球谐函数相互正交,并且归一化使得它们在整个球面上的平方积分等于 1:
此处星号表示复共轭。
从数学上讲,球谐函数与连带勒让德多项式通过以下公式相关:
利用关系式
我们总可以将一个球谐函数与 的连带勒让德多项式联系起来。令 ,这些连带勒让德多项式由普通勒让德多项式(参见 §4.6 和 §5.4)定义为:
注意:连带勒让德多项式存在不同的归一化方式和符号约定。
前几个连带勒让德多项式及其对应的归一化球谐函数如下:
数值计算连带勒让德多项式有许多不佳的方法。例如,存在显式表达式,如:
其中多项式展开至 项为止。(参见 [1] 中的相关公式。)这种方法并不理想,因为多项式的计算涉及连续项之间微妙的相消,而这些项符号交替。当 较大时,多项式中的各项远大于其总和,导致精度完全丧失。
实际上,公式 (6.7.6) 在单精度(32 位)下仅适用于 不超过 6 或 8 的情况,在双精度(64 位)下仅适用于 不超过 15 或 18 的情况,具体取决于结果所需的精度。因此,需要一种更稳健的计算方法,如下所述。
连带勒让德函数满足大量递推关系,这些关系在 [1,2] 中有详细列表。这些递推关系可以仅对 、仅对 ,或同时对 和 进行。大多数涉及 的递推关系是不稳定的,因此不适合数值计算。然而,以下仅对 的递推关系是稳定的(参见 5.4.1):
即使如此,该递推关系也仅适用于中等大小的 和 ,因为 本身随 快速增长并迅速溢出。相比之下,球谐函数是有界的——毕竟它们被归一化为 1(见公式 6.7.1)。公式 (6.7.2) 中的平方根因子恰好抵消了这种发散。因此,在递推关系中应使用重归一化的连带勒让德函数:
于是递推关系 (6.7.7) 变为:
我们从 时的闭式表达式开始递推:
(记号 表示所有小于或等于 的奇数的乘积。)将 (6.7.9) 应用于 ,并设 ,可得:
公式 (6.7.10) 和 (6.7.11) 为一般 的递推关系 (6.7.9) 提供了所需的两个初始值。
实现该算法的函数如下:
Doub plegendre(const Int l, const Int m, const Doub x) {
// 计算重归一化的连带勒让德多项式 $\widetilde{P}_{l}^{m}(x)$,见公式 (6.7.8)。
// 其中 $m$ 和 $l$ 为满足 $0 \leq m \leq l$ 的整数,$x$ 的取值范围为 $-1 \leq x \leq 1$。
static const Doub PI = 3.141592653589793;
Int i, ll;
Doub fact, oldfact, pll, pmm, pmm1, omx2;
if (m < 0 || m > l || abs(x) > 1.0)
throw("Bad arguments in routine plgndr");
pmm = 1.0;
if (m > 0) {
omx2 = (1.0 - x) * (1.0 + x);
fact = 1.0;
for (i = 1; i <= m; i++) {
pmm *= omx2 * fact / (fact + 1.0);
fact += 2.0;
}
}
pmm = sqrt((2 * m + 1) * pmm / (4.0 * PI));
if (m & 1)
pmm = -pmm;
if (l == m)
return pmm;
else {
// 计算 $\tilde{P}_{m+1}^{m}$。
pmm1 = x * sqrt(2.0 * m + 3.0) * pmm;
if (l == (m + 1))
return pmm1;
else {
// 计算 $\tilde{P}_{l}^{m}$,其中 $l > m + 1$。
oldfact = sqrt(2.0 * m + 3.0);
for (ll = m + 2; ll <= l; ll++) {
fact = sqrt((4.0 * ll * ll - 1.0) / (ll * ll - m * m));
pll = (x * pmm1 - pmm / oldfact) * fact;
oldfact = fact;
pmm = pmm1;
pmm1 = pll;
}
return pll;
}
}
}
有时使用标准归一化的函数更为方便,即由公式 (6.7.4) 定义的形式。以下是一个实现该功能的例程。注意,当 时会发生溢出,若 ,则溢出可能更早发生。
Doub plgndr(const Int l, const Int m, const Doub x)
计算连带勒让德多项式 ,见公式 (6.7.4)。其中 和 为满足 的整数,而 的取值范围为 。当 时,这些函数会发生溢出。
const Doub PI = 3.141592653589793238;
if (m < 0 || m > l || abs(x) > 1.0)
throw("Bad arguments in routine plgndr");
Doub prod = 1.0;
for (Int j = l - m + 1; j <= l + m; j++)
prod *= j;
return sqrt(4.0 * PI * prod / (2 * l + 1)) * plegendre(l, m, x);
6.7.1 快速球谐变换
球面上任意光滑函数均可展开为球谐函数级数。假设该函数可通过截断至 的展开式得到良好近似:
此处函数在 个采样点 和 个采样点 处取值。总采样点数为 。在实际应用中,通常有 。由于求和式 (6.7.12) 中球谐函数的总数为 ,因此也有 。
计算求和式 (6.7.12) 需要多少次运算?在 个采样点上直接计算 项是一个 的过程。你可以尝试通过将 选为等间距角度点,并利用 FFT 计算对 的求和来加速。每次 FFT 的复杂度为 ,而你需要执行 次,总运算量为 ,这已有一定改进。通过一个简单的求和顺序交换 [3–5] 可获得更优方法:
从而得到:
其中
计算式 (6.7.15) 中的求和需要 次运算,而需要对 个 进行计算,因此总计算量为 。对于固定的 ,通过 FFT 计算式 (6.7.14) 的复杂度为 。总共需执行 次 FFT,总运算量为 ,相比之下可忽略不计。因此整个算法的复杂度为 。注意,你可以通过递推关系 (6.7.9) 预先计算并存储 ,或者使用 Clenshaw 方法(§5.4)来计算式 (6.7.14)。
那么如何对变换 (6.7.12) 进行反演呢?对于连续函数 的展开,其形式上的逆变换可由 的正交归一性(公式 (6.7.1))导出:
对于离散情形,即函数已被采样,积分变为数值求积:
其中 为求积权重。原则上权重也可依赖于 ,但在实际中我们通过 FFT 进行 方向的求积,因此权重为 1。对于 方向的等角网格,文献 [3] 的定理 3 给出了一个良好的权重选择。另一种可能是对 积分使用高斯求积。此时,应选择采样点使得 为 gauleg 返回的横坐标,而 为对应的权重。计算的最佳组织方式是首先进行 FFT,计算:
然后
可以验证,总运算量由式 (6.7.19) 主导,再次呈现 的复杂度。在实际计算中,应充分利用各种对称性以减少计算量,例如 以及 。
最近,人们发展出了类似于 FFT 的快速勒让德变换算法 [3,6,7]。理论上,这些算法可将正向和逆向球谐变换的复杂度降至 。然而,目前的实现 [8] 在 时相比上述 方法并未快很多,且存在稳定性与精度问题,需谨慎处理 [9]。敬请关注!
参考文献
Magnus, W., and Oberhettinger, F. 1949, Formulas and Theorems for the Functions of Mathematical Physics (New York: Chelsea), pp. 54ff.[1]
Abramowitz, M., and Stegun, I.A. 1964, Handbook of Mathematical Functions (Washington: National Bureau of Standards); reprinted 1968 (New York: Dover); online at http://www.nr.com/aands, Chapter 8.[2]
Driscoll, J.R., and Healy, D.M. 1994, "Computing Fourier Transforms and Convolutions on the 2-sphere," Advances in Applied Mathematics, vol. 15, pp. 202–250.[3]
Muciaccia, P.F., Natoli, P., and Vittorio, N. 1997, "Fast Spherical Harmonic Analysis: A Quick Algorithm for Generating and/or Inverting Full-Sky, High-Resolution Cosmic Microwave Background Anisotropy Maps," Astrophysical Journal, vol. 488, pp. L63–66.[4]
Oh, S.P., Spergel, D.N., and Hinshaw, G. 1999, "An Efficient Technique to Determine the Power Spectrum from Cosmic Microwave Background Sky Maps," Astrophysical Journal, vol. 510, pp. 551–563, Appendix A.[5]
Healy, D.M., Rockmore, D., Kostelec, P.J., and Moore, S. 2003, "FFTs for the 2-Sphere: Improvements and Variations," Journal of Fourier Analysis and Applications, vol. 9, pp. 341–385.[6]
Potts, D., Steidl, G., and Tasche, M. 1998, "Fast and Stable Algorithms for Discrete Spherical Fourier Transforms," Linear Algebra and Its Applications, vol. 275-276, pp. 433–450.[7]
Moore, S., Healy, D.M., Rockmore, D., and Kostelec, P.J. 2007+, SphaeronicKit. Software at http://www.cs.dartmouth.edu/~geelong/sphere.[8]
Healy, D.M., Kostelec, P.J., and Rockmore, D. 2004, "Towards Safe and Effective High-Order Legendre Transforms with Applications to FFTs for the 2-Sphere," Advances in Computational Mathematics, vol. 21, pp. 59–105.[9]
6.8 菲涅耳积分、余弦积分和正弦积分
6.8.1 菲涅耳积分
两个菲涅耳积分定义为
其图像见图 6.8.1。
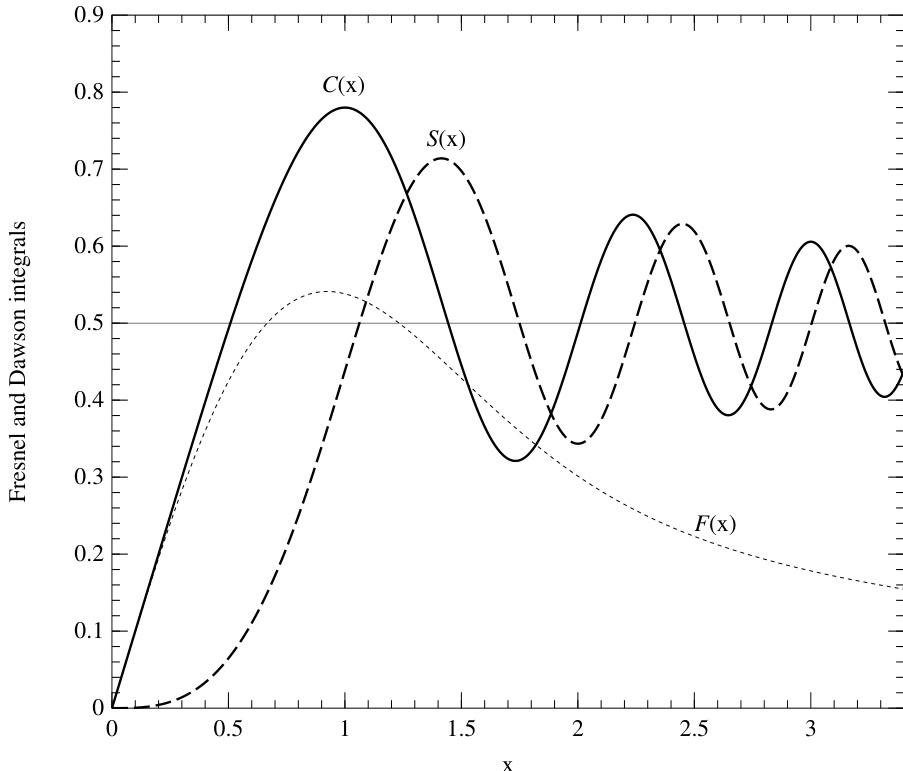
图 6.8.1. 菲涅耳积分 和 (§6.8),以及道森积分 (§6.9)。
对任意精度计算这些函数最方便的方法是:对小的 使用幂级数,对大的 使用连分式。幂级数为
存在一个复连分式可同时计算 和 :
其中
最后一行中,我们将连分式的“标准”形式转换为其“偶数”形式(见 §5.2),其收敛速度提高了一倍。我们必须注意不要在过大的 值处使用交错级数(6.8.2);通过观察各项可知, 是切换到连分式的合适点。
注意,当 很大时,
因此,对于大的 ,函数 frenel 的精度可能受限于库函数中正弦和余弦函数的精度。
Complex frenel(const Doub x) {
// 计算所有实数 x 的菲涅耳积分 S(x) 和 C(x)。
// C(x) 作为 cs 的实部返回,S(x) 作为虚部返回。
static const Int MAXIT=100;
static const Doub PI=3.141592653589793238, PIBY2=(PI/2.0), XMIN=1.5,
EPS=numeric_limits<Doub>::epsilon(),
FPMIN=numeric_limits<Doub>::min(),
BIG=numeric_limits<Doub>::max()*EPS;
// MAXIT 是允许的最大迭代次数;EPS 是相对误差;
// FPMIN 是接近最小可表示浮点数的数;BIG 是接近机器溢出限的数;
// XMIN 是使用级数与连分式的分界点。
Bool odd;
Int k,n;
Doub a,ax,fact,pix2,sign,sum,sumc,sums,term,test;
Complex b,cc,d,h,del,cs;
if ((ax=abs(x)) < sqrt(FPMIN)) {
cs=ax;
}
else if (ax <= XMIN) {
sumc=sums=0.0;
sum=ax;
sign=1.0;
fact=PIBY2*ax*ax;
odd=true;
term=ax;
n=3;
for (k=1;k<=MAXIT;k++) {
term *= fact/k;
sum += sign*term/n;
test=abs(sum)*EPS;
if (odd) {
sign = -sign;
sums=sum;
sum=sumc;
} else {
sumc=sum;
sum=sums;
}
if (term < test) break;
odd=!odd;
n += 2;
}
if (k > MAXIT) throw("series failed in frenel");
cs=Complex(sumc,sums);
}
else {
pix2=PI*ax*ax;
b=Complex(1.0,-pix2);
cc=BIG;
d=h=1.0/b;
n = -1;
for (k=2;k<=MAXIT;k++) {
n += 2;
a = -n*(n+1);
b += 4.0;
d=1.0/(a*d+b);
cc=b+a/cc;
del=cc*d;
h *= del;
if (abs(real(del)-1.0)+abs(imag(del)) <= EPS) break;
}
if (k > MAXIT) throw("cf failed in frenel");
h *= Complex(ax,-ax);
cs=Complex(0.5,0.5)
*(1.0-Complex(cos(0.5*pix2),sin(0.5*pix2))*h);
}
if (x < 0.0) cs = -cs;
return cs;
}
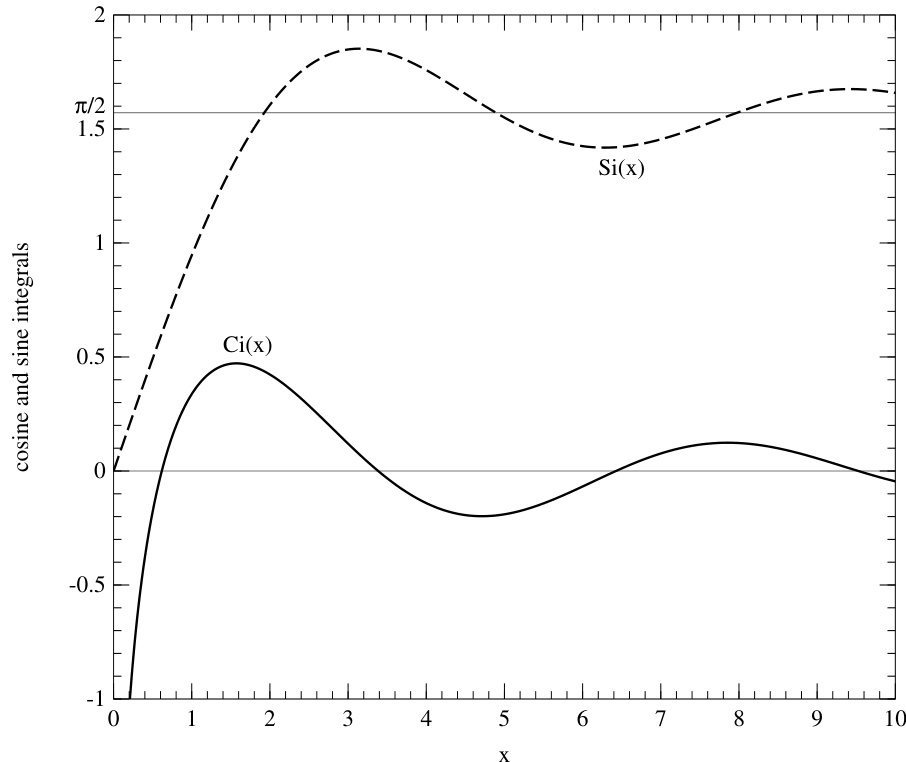
图 6.8.2. 正弦积分 Si(x) 和余弦积分 Ci(x)。
6.8.2 余弦积分和正弦积分
余弦积分和正弦积分定义为
其图像见图 6.8.2。其中 为欧拉常数。我们只需计算 时的函数值,因为
同样,我们可以通过幂级数与连分式的巧妙组合来计算这些函数。
级数与复连分式。这些级数为:
指数积分 的连分式为:
最后一行给出的是连分式的“偶数”形式,其收敛速度约为相同计算量下前一种形式的两倍。在此情形下,从交错级数切换到连分式的良好分界点为 。至于菲涅耳积分,当 较大时,精度可能受限于正弦和余弦函数的计算精度。
计算余弦积分 与正弦积分 。函数 作为复数 cs 的实部返回, 作为其虚部返回。 返回一个很大的负数,且不产生错误信息。对于 ,该例程返回 ,此时需自行添加 。
其中,Euler 为欧拉常数 ;PIBY2 为 ;TMIN 为使用级数与连分式的分界点;EPS 为相对误差(或在 零点附近的绝对误差);FPMIN 为接近最小可表示浮点数的数值;BIG 为接近机器溢出极限的数值。
Int i, k;
Bool odd;
Doub a, err, fact, sign, sums, sumc, t, term;
Complex h, b, c, d, del, cs;
if ((t = abs(x)) == 0.0) return -BIG;
if (t > TMIN) {
b = Complex(1.0, t);
c = Complex(BIG, 0.0);
d = h = 1.0 / b;
for (i = 1; i <= MAXIT; i++) {
a = -i * i;
b += 2.0;
d = 1.0 / (a * d + b);
c = b + a / c;
del = c * d;
h *= del;
if (abs(real(del) - 1.0) + abs(imag(del)) <= EPS) break;
}
if (i >= MAXIT) throw("cf failed in cisi");
h = Complex(cos(t), -sin(t)) * h;
cs = -conj(h) + Complex(0.0, PIBY2);
} else {
// 同时计算两个级数。
if (t < sqrt(FPMIN)) {
sumc = 0.0;
sums = t;
} else {
sum = sums = sumc = 0.0;
sign = fact = 1.0;
odd = true;
for (k = 1; k <= MAXIT; k++) {
fact *= t / k;
term = fact / k;
sum += sign * term;
err = term / abs(sum);
if (odd) {
sign = -sign;
sums = sum;
sum = sumc;
} else {
sumc = sum;
sum = sums;
}
if (err < EPS) break;
odd = !odd;
}
if (k > MAXIT) throw("maxits exceeded in cisi");
}
cs = Complex(sumc + log(t) + EULER, sums);
}
if (x < 0.0) cs = conj(cs);
return cs;
参考文献
Stegun, I.A., and Zucker, R. 1976, "Automatic Computing Methods for Special Functions. III. The Sine, Cosine, Exponential integrals, and Related Functions," Journal of Research of the National Bureau of Standards, vol. 80B, pp. 291–311; 1981, "Automatic Computing Methods for Special Functions. IV. Complex Error Function, Fresnel Integrals, and Other Related Functions," op. cit., vol. 86, pp. 661–686.
Abramowitz, M., and Stegun, I.A. 1964, Handbook of Mathematical Functions (Washington: National Bureau of Standards); reprinted 1968 (New York: Dover); online at http://www.nr.com/aands, Chapters 5 and 7.
6.9 道森积分
道森积分 定义为:
函数图像见图 6.8.1。该函数也可通过复误差函数表示为:
Rybicki [1] 提出了一种对 的卓越近似:
公式 (6.9.3) 的特别之处在于,当 变小时,其精度呈指数级提高,因此即使取适中的 值(相应地级数收敛也很快),也能得到非常精确的近似。
我们将在第 13.11 节中讨论导出公式 (6.9.3) 的理论,作为傅里叶方法的一个有趣应用。此处我们仅基于该公式实现一个用于实数 的计算例程。
首先,将求和指标平移,使其大致对准指数项的最大值位置较为方便。令 为最接近 的偶数,定义 ,,以及 ,于是有:
当 足够小且 足够大时,上述近似是准确的。若注意到:
则可大幅加速该公式的计算:第一项只需计算一次,第二项是一组需存储的常数,第三项可通过递推计算,因此只需计算两个指数函数。此外,还可利用系数 的对称性,将求和拆分为 的正负部分分别处理。
在以下例程中,取 且 。由于求和的对称性及 仅取奇数值的限制,循环的上下限为 0 到 5。此版本结果的精度约为 。为在 附近(此时 趋于零)保持相对精度,程序在 时转而使用 的幂级数展开 [2]。
Doub dawson(const Doub x) {
// 返回道森积分 $F(x)=\exp(-x^{2})\int_{0}^{x}\exp(t^{2})dt$,适用于任意实数 $x$。
static const Int NMAX = 6;
static VecDoub c(NMAX);
static Bool init = true;
static const Doub H = 0.4, A1 = 2.0 / 3.0, A2 = 0.4, A3 = 2.0 / 7.0;
Int i, n0;
// Flag is true if we need to initialize, else false.
Doub d1, d2, e1, e2, sum, x2, xp, xx, ans;
if (init) {
init = false;
for (i = 0; i < NMAX; i++) c[i] = exp(-SQR((2.0 * i + 1.0) * H));
}
if (abs(x) < 0.2) {
x2 = x * x;
ans = x * (1.0 - A1 * x2 * (1.0 - A2 * x2 * (1.0 - A3 * x2)));
} else {
xx = abs(x);
n0 = 2 * Int(0.5 * xx / H + 0.5);
xp = xx - n0 * H;
e1 = exp(2.0 * xp * H);
e2 = e1 * e1;
d1 = n0 + 1;
d2 = d1 - 2.0;
sum = 0.0;
for (i = 0; i < NMAX; i++, d1 += 2.0, d2 -= 2.0, e1 *= e2)
sum += c[i] * (e1 / d1 + 1.0 / (d2 * e1));
ans = 0.5641895835 * SIGN(exp(-xp * xp), x) * sum;
}
return ans;
}
其他计算道森积分的方法亦有文献记载 [2,3]。
参考文献
Rybicki, G.B. 1989, "Dawson积分与采样定理," Computers in Physics, 第3卷, 第2期, 第85–87页。[1]
Cody, W.J., Pociorek, K.A., 和 Thatcher, H.C. 1970, "Dawson积分的切比雪夫逼近," Mathematics of Computation, 第24卷, 第171–178页。[2]
McCabe, J.H. 1974, "Dawson积分的一个连分式展开及其截断误差估计," Mathematics of Computation, 第28卷, 第811–816页。[3]
6.10 广义费米-狄拉克积分
广义费米-狄拉克积分定义为
例如,在天体物理应用中会出现该积分,其中 非负, 为任意值。在凝聚态物理中,通常采用更简单的情形 ,此时函数名称中省略“广义”二字。重要的 值为 、、 和 ,但我们将考虑所有大于 的任意 值。注意存在另一种定义,该定义将积分乘以 。
当 和 时,这些函数有实用的级数展开式(参见,例如 [1])。例如,
此处 由下式定义:
最难处理的是 的中间取值范围。
对于 的情形,Macleod [2] 给出了针对四个重要 值的切比雪夫展开式,精度可达 ,覆盖所有 值。在此情况下,无需再寻找其他算法。Goano [3] 则处理了 时任意 的情形。对于非零 ,
通过直接积分计算这些函数是合理的,可采用变量变换以获得快速收敛的数值积分 [4]。(当然,该方法也适用于 ,但效率较低。)常用的变换 可处理 处的奇点以及大 时的指数衰减(参见公式 4.5.14)。当 时,将积分拆分为两个区间 和 更为合适。( 之后的贡献可忽略不计。)每个积分均可使用 DE 规则进行计算。使用 60 至 500 次函数求值即可达到完整的双精度,更大的 需要更多的函数求值次数。更高效的策略是在大 时用级数展开替代数值积分。
在下面的实现中,请注意 operator() 是如何重载的,以同时定义单变量函数(用于 Trapzd)和双变量函数(用于 DErule)。同时注意以下语法:
struct Fermi {
Doub KK, etaa, thetaaa;
Doub operator() (const Doub t);
Doub operator() (const Doub x, const Doub del);
Doub val(const Doub k, const Doub eta, const Doub theta);
};
Doub Fermi::operator() (const Doub t) {
// 广义费米-狄拉克积分的梯形积分法被积函数,使用变换 x = exp(t - exp(-t))。
Doub x;
x = exp(t - exp(-t));
return x * (1.0 + exp(-t)) - pow(x, kk) * sqrt(1.0 + thetaaa * 0.5 * x) / (exp(x - etaa) + 1.0);
}
Doub Fermi::operator() (const Doub x, const Doub del) {
// 广义费米-狄拉克积分的 DE 规则被积函数。
if (x < 1.0)
return pow(x, kk) * sqrt(1.0 + thetaaa * 0.5 * x) / (exp(x - etaa) + 1.0);
else
return pow(x, kk) * sqrt(1.0 + thetaaa * 0.5 * x) / (exp(x - etaa) + 1.0);
}
计算广义费米-狄拉克积分 ,其中 且 。精度约为参数 EPS 的平方。NMAX 限制了数值积分的总步数。
const Doub EPS = 3.0e-9;
const Int NMAX = 11;
Doub a, aa, b, bb, hmax, olds, sum;
kk = k;
etaa = eta;
thetaaa = theta;
if (eta <= 15.0) {
a = -4.5;
b = 5.0;
Trapzd<Fermi> s(*this, a, b);
for (Int i = 1; i <= NMAX; i++) {
sum = s.next();
if (i > 3)
if (abs(sum - olds) <= EPS * abs(olds))
return sum; // 将参数加载到成员变量中,供函数求值使用。
olds = sum; // 保存值用于下一次收敛性检验。
}
} else {
a = 0.0;
b = eta;
aa = eta;
bb = eta + 60.0;
hmax = 4.3;
DErule<Fermi> s(*this, a, b, hmax);
DErule<Fermi> ss(*this, aa, bb, hmax);
for (Int i = 1; i <= NMAX; i++) {
sum = s.next() + ss.next();
if (i > 3)
if (abs(sum - olds) <= EPS * abs(olds))
return sum;
olds = sum;
}
}
throw("fermi 中未收敛");
return 0.0;
通过声明一个 Fermi 对象即可获得费米-狄拉克函数的值:
Fermi ferm;
然后重复调用 val 函数:
ans = ferm.val(k, eta, theta);
这些函数还有其他数值积分方法 [5–7]。一种较为高效的方法 [8] 涉及带“极点修正”的梯形积分法,但仅适用于 。广义玻色-爱因斯坦积分也可通过 DE 规则或上述文献中的方法进行计算。
参考文献
Cox, J.P., 和 Giuli, R.T. 1968, 恒星结构原理(纽约:Gordon and Breach),第 II 卷,§24.7。[1]
Macleod, A.J. 1998, "阶数为 、、、 的费米-狄拉克函数," ACM Transactions on Mathematical Software, 第24卷, 第1–12页。(算法 779,可从 netlib 获取。)[2]
Goano, M. 1995, "完整与非完整费米-狄拉克积分的计算," ACM Transactions on Mathematical Software, 第21卷, 第221–232页。(算法 745,可从 netlib 获取。)[3]
Natarajan, A., and Kumar, N.M. 1993, "On the Numerical Evaluation of the Generalised Fermi-Dirac Integrals," Computer Physics Communications, vol. 76, pp. 48–50.[4]
Pichon, B. 1989, "Numerical Calculation of the Generalized Fermi-Dirac Integrals," Computer Physics Communications, vol. 55, pp. 127–136.[5]
Sagar, R.P. 1991, "A Gaussian Quadrature for the Calculation of Generalized Fermi-Dirac Integrals," Computer Physics Communications, vol. 66, pp. 271–275.[6]
Gautschi, W. 1992, "On the Computation of Generalized Fermi-Dirac and Bose-Einstein Integrals," Computer Physics Communications, vol. 74, pp. 233–238.[7]
Mohankumar, N., and Natarajan, A. 1996, "A Note on the Evaluation of the Generalized Fermi-Dirac Integral," Astrophysical Journal, vol. 458, pp. 233–235.[8]
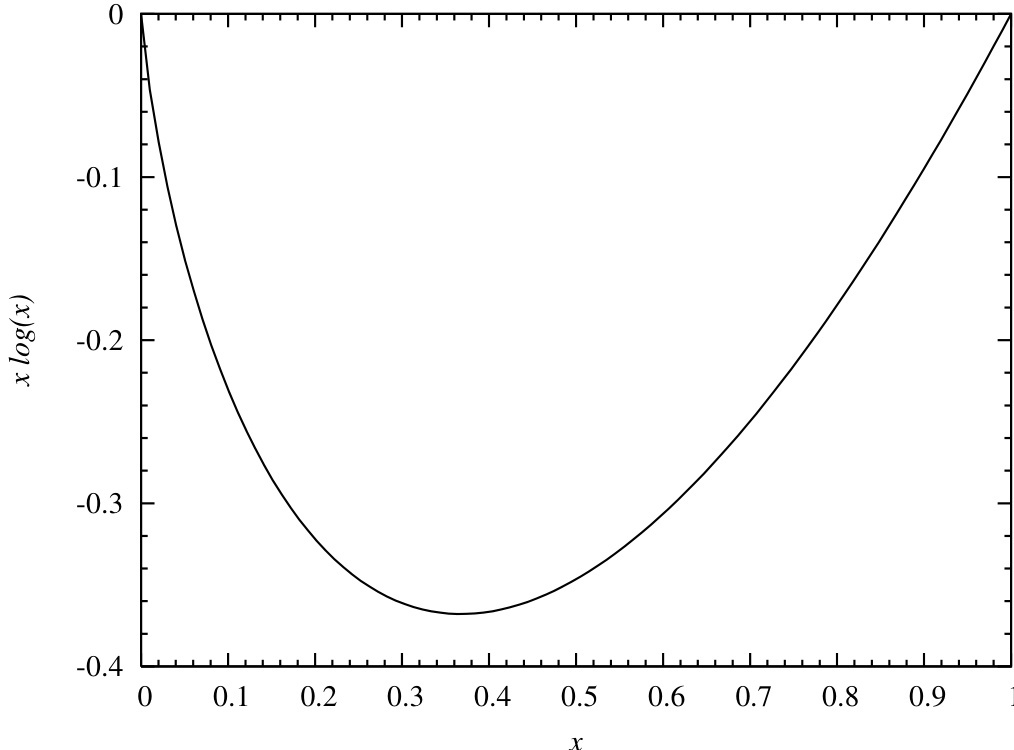
图 6.11.1. 函数 在区间 上的图像。尽管几乎不可见,但在 处存在一个本性奇点,使得该函数难以求逆。
6.11 函数 的反函数
函数
及其反函数 出现在许多统计学和信息论的场景中。显然,对于所有正的 , 是无奇点的,并且易于计算。当 介于 0 和 1 之间时,该函数为负值,在点 处取得唯一极小值。函数在 处取值为 0,并且当 时其极限也为 0,因为线性因子 能够轻易压倒对数项的奇异性。
然而,计算反函数 却并不容易。(我们将在 §6.14.12 中需要用到这个反函数。)从图 6.11.1 的外观来看,似乎很容易对函数的左支进行求逆,即对于每个介于 0 和 之间的 值,返回一个介于 0 和 之间的 值。然而,隐藏在 处的对数奇点会给许多尝试使用的方法带来困难。
多项式拟合在 的变化范围不超过一个数量级左右(例如从 0.01 到 0.1)时效果很好,但若要求高相对精度并延伸至 ,则会严重失效。
那么牛顿法如何呢?我们写出
从而得到迭代公式
这种方法行不通。问题不在于其收敛速度——对于任何有限的 ,只要初始值足够接近解,它当然具有二次收敛速度(见 §9.4)。问题在于其收敛区域非常小,尤其是当 时。因此,如果我们接近奇点时还没有一个较好的近似值,就会陷入困境。
如果我们进行变量替换,就可以得到牛顿法的不同形式(在计算上并不等价)。例如,令
在变量 下的牛顿法如下:
但事实证明,迭代式 (6.11.5) 并不比 (6.11.3) 更好。
一个关键的观察是:由于对数项变化缓慢,当以双对数坐标绘制时, 的曲率非常小。(实际上绘制的是 ,因为双对数坐标要求量值为正。)从代数上,我们将方程 (6.11.1) 重写为
(其中 如上定义),然后取对数,得到
由此导出牛顿迭代公式:
事实证明,迭代式 (6.11.8) 在相当宽泛的初始猜测范围内都能实现二次收敛。对于 ,可以简单地选择一个固定的初始猜测值,例如 。当 时,可以使用在 附近的泰勒级数展开:
由此得到
利用这些初始猜测,式 (6.11.8) 收敛到双精度精度所需的迭代次数从不超过六次,且每次迭代仅需一次对数运算和若干次算术运算。其实现如下:
Doub invxlogx(Doub y) {
// 对于负的 y,满足 0 > y > -e^{-1},返回 x 使得 y = x log(x)。
// 返回的值始终是两个根中较小的那个,且位于区间 0 < x < e^{-1} 内。
const Doub ooe = 0.367879441171442322;
Doub t, u, to = 0.;
if (y >= 0. || y <= -ooe) throw("no such inverse value");
if (y < -0.2)
u = log(ooe - sqrt(2 * ooe * (y + ooe))); // 通过泰勒级数的反函数给出初值。
else
u = -10.;
do {
u += (t = (log(y / u) - u) * (u / (1. + u)));
if (t < 1.e-8 && abs(t + to) < 0.01 * abs(t)) break;
to = t;
} while (abs(t / u) > 1.e-15);
return exp(u);
}
6.12 椭圆积分与雅可比椭圆函数
椭圆积分在许多应用中都会出现,因为任何形如
的积分,其中 是 和 的有理函数,而 是 的三次或四次多项式的平方根,都可以用椭圆积分来表示。标准参考文献 [1] 描述了如何进行这种化简,这一工作最初由勒让德(Legendre)完成。勒让德指出,只需三种基本的椭圆积分即可。其中最简单的是
这里我们将四次多项式 写成了因式分解的形式。在标准积分表 [2] 中,积分限之一总是四次多项式的一个零点,而另一个积分限则位于比下一个零点更近的位置,从而保证积分区间内无奇点。为了计算 ,我们只需将区间 分割成若干子区间,每个子区间都以一个奇点作为起点或终点。因此,积分表只需区分八种情形,即四个零点(按大小排序)中每一个作为积分上限或下限时的情形。此外,当式 (6.12.2) 中某个 趋近于零时,四次多项式退化为三次多项式,此时最大或最小的奇点移至 ;这又引出另外八种情形(实际上只是前八种的特例)。总共 16 种情形通常用勒让德第一类标准椭圆积分来列表表示,我们将在下文定义该积分。通过变量替换 ,可将四次多项式的零点映射到实轴上的标准位置,因此只需两个无量纲参数即可列表表示勒让德积分。然而,原始积分 (6.12.2) 在根置换下的对称性在勒让德记号中被掩盖了。我们稍后再回到勒让德记号。但首先,这里有一种更好的方法:
卡尔森(Carlson)[3] 给出了第一类标准椭圆积分的新定义:
其中 、 和 为非负数,且至多一个为零。通过将积分区间标准化,他保留了零点的置换对称性。(魏尔斯特拉斯(Weierstrass)的标准形式也具有这一性质。)卡尔森首先证明,当 或 是式 (6.12.2) 中四次多项式的一个零点时,积分 可以用 表示,且形式在其余三个零点的置换下对称。在一般情形下,当 和 均非零点时,可通过加法定理将两个这样的 函数合并为一个,从而得到基本公式:
其中
且 、、、 是 的任意排列。计算这些表达式的一个捷径是:
这些 对应于将四个零点配对的三种方式,因此 在零点置换下显然对称。因此,式 (6.12.4) 不仅涵盖了当一个积分限为零点时的全部 16 种情形,也包括了两个积分限均非零点的情形。
因此,卡尔森函数允许任意的积分区间,以及被积函数的支点相对于积分区间任意的位置。为了处理第二类和第三类椭圆积分,卡尔森将第三类标准积分定义为:
该函数在 、 和 中对称。当其中两个参数相等时的退化情形记为:
它在 和 中对称。函数 取代了勒让德的第二类积分。 的退化形式记为:
它包含了对数函数、反三角函数和反双曲函数。
卡尔森 [4–7] 给出了用式 (6.12.1) 中四次多项式线性因子的指数表示的积分表。例如,当指数为 时,该积分可用单个 积分表示;它涵盖了 Gradshteyn 和 Ryzhik [2] 中的 144 种不同情形!
关于将椭圆积分化简为卡尔森标准形式的一些实际细节(例如处理共轭复零点),请参阅卡尔森的论文 [3–8]。
现在转向椭圆积分的数值计算。传统方法 [9] 是高斯变换或兰登(Landen)变换。下降变换使勒让德积分的模 趋近于零,而上升变换使其趋近于 1。在这两种极限情形下,函数具有简单的解析表达式。尽管这些方法具有二次收敛性,对于第一类和第二类积分相当令人满意,但在某些情形下,对于第三类积分通常会导致有效数字的损失。相比之下,卡尔森的算法 [10,11] 为所有三类积分提供了一种统一的方法,且不会出现显著的相消误差。
这些算法的关键在于倍加定理(duplication theorem):
其中
该定理可通过简单的积分变量替换加以证明 [12]。重复应用公式 (6.12.11),直到 的三个参数几乎相等。当参数相等时,有
当参数足够接近时,函数值通过围绕 (6.12.13) 的五阶泰勒展开式计算。尽管算法的迭代部分仅具有线性收敛性,但每次迭代后误差最终会减小 倍。通常只需两到三次迭代;若初始参数的比值极大,最多也只需六到七次迭代。我们在此列出 的算法,其他情形请参阅 Carlson 的论文 [10]。
阶段 1:对 ,计算
若 ,则进入阶段 2;否则计算
并重复此阶段。
阶段 2:计算
在某些应用中, 中的参数 或 中的参数 可能为负,此时需要计算积分的柯西主值(Cauchy principal value)。这可通过以下公式轻松处理:
其中
当 为负时, 为正;以及
的柯西主值在某个 处存在零点,因此公式 (6.12.14) 在该零点附近会导致有效数字的部分损失。
Doub rf(const Doub x, const Doub y, const Doub z) {
// 计算 Carlson 第一类椭圆积分 R_F(x,y,z)。
// x, y, z 必须非负,且至多一个为零。
static const Doub ERRROL = 0.0025, THIRD = 1.0/3.0, C1 = 1.0/24.0, C2 = 0.1, C3 = 3.0/44.0, C4 = 1.0/14.0;
static const Doub TINY = 5.0 * numeric_limits<Doub>::min(), BIG = 0.2 * numeric_limits<Doub>::max();
Doub alamb, ave, delx, dely, delz, e2, e3, sqrtx, sqrty, sqrtz, xt, yt, zt;
if (min(min(x, y), z) < 0.0 || min(min(x + y, x + z), y + z) < TINY || max(max(x, y), z) > BIG)
throw("invalid arguments in rf");
xt = x;
yt = y;
zt = z;
do {
sqrtx = sqrt(xt);
sqrty = sqrt(yt);
sqrtz = sqrt(zt);
alamb = sqrtx * (sqrty + sqrtz) + sqrty * sqrtz;
xt = 0.25 * (xt + alamb);
yt = 0.25 * (yt + alamb);
zt = 0.25 * (zt + alamb);
ave = THIRD * (xt + yt + zt);
delx = (ave - xt) / ave;
dely = (ave - yt) / ave;
delz = (ave - zt) / ave;
} while (max(max(abs(delx), abs(dely)), abs(delz)) > ERRROL);
e2 = delx * dely - delz * delz;
e3 = delx * dely * delz;
return (1.0 + (C1 * e2 - C2 - C3 * e3) * e2 + C4 * e3) / sqrt(ave);
}
将误差容限参数设为 0.0025 可获得完整的双精度(16 位有效数字)。由于误差按 缩放,可见单精度(7 位有效数字)下 0.08 已足够,但最多仅能节省两到三次迭代。由于其他椭圆函数的六阶截断误差系数不同,对于 算法,误差容限应设为 0.04(单精度)或 0.0012(双精度);对于 和 ,则应设为 0.05 或 0.0015。 算法不仅本身可用于某些初等函数组合的计算,还在 的计算中被反复调用。
C++ 实现通过两个与机器相关的常数 TINY 和 BIG 对输入参数进行检验,以确保计算过程中不会发生下溢或上溢。你总可以通过下面的齐次关系式 (6.12.22) 来扩展允许的参数范围。
Doub rd(const Doub x, const Doub y, const Doub z) {
// 计算 Carlson 第二类椭圆积分 R_D(x,y,z)。
// x 和 y 必须非负,且至多一个为零。z 必须为正。
static const Doub ERRROL = 0.0015, C1 = 3.0/14.0, C2 = 1.0/6.0, C3 = 9.0/22.0,
C4 = 3.0/26.0, C5 = 0.25 * C3, C6 = 1.5 * C4;
static const Doub TINY = 2.0 * pow(numeric_limits<Doub>::max(), -2.0/3.0),
BIG = 0.1 * ERRROL * pow(numeric_limits<Doub>::min(), -2.0/3.0);
Doub alamb, ave, delx, dely, delz, ea, eb, ec, ed, ee, fac, sqrtx, sqrty,
sqrtz, sum, xt, yt, zt;
if (min(x, y) < 0.0 || min(x + y, z) < TINY || max(max(x, y), z) > BIG)
throw("invalid arguments in rd");
xt = x;
yt = y;
zt = z;
sum = 0.0;
fac = 1.0;
do {
sqrtx = sqrt(xt);
sqrty = sqrt(yt);
sqrtz = sqrt(zt);
alamb = sqrtx * (sqrty + sqrtz) + sqrty * sqrtz;
sum += fac / (sqrtz * (zt + alamb));
fac = 0.25 * fac;
xt = 0.25 * (xt + alamb);
yt = 0.25 * (yt + alamb);
zt = 0.25 * (zt + alamb);
ave = 0.2 * (xt + yt + 3.0 * zt);
delx = (ave - xt) / ave;
dely = (ave - yt) / ave;
delz = (ave - zt) / ave;
} while (max(max(abs(delx), abs(dely)), abs(delz)) > ERRROL);
ea = delx * dely;
eb = delz * delz;
ec = ea - eb;
ed = ea - 6.0 * eb;
ee = ed + ec + ec;
return 3.0 * sum * fac * (1.0 + ed * (-C1 + C5 * ed - C6 * delz * ee)
+ delz * (C2 * ee + delz * (-C3 * ec + delz * C4 * ea))) / (ave * sqrt(ave));
}
Doub rj(const Doub x, const Doub y, const Doub z, const Doub p) {
// 计算 Carlson 第三类椭圆积分 R_J(x,y,z,p)。
// x, y, z 必须非负,且至多一个为零。p 必须非零。
// 若 p < 0,则返回柯西主值。
static const Doub ERRROL = 0.0015, C1 = 3.0/14.0, C2 = 1.0/3.0, C3 = 3.0/22.0, C4 = 3.0/26.0,
C5 = 0.75 * C3, C6 = 1.5 * C4, C7 = 0.5 * C2, C8 = C3 + C3;
static const Doub TINY = pow(5.0 * numeric_limits<Doub>::min(), 1.0/3.0),
BIG = 0.3 * pow(0.2 * numeric_limits<Doub>::max(), 1.0/3.0);
Doub alamb, alpha, ans, ave, beta, delx, dely, delz, ea, eb, ec, ed, ee, f, pt, rcx, rho,
sqrtx, sqrty, sqrtz, sum, tau, xt, yt, zt;
if (min(min(x, y), z) < 0.0 || min(min(x + y, x + z), min(y + z, abs(p))) < TINY ||
max(max(x, y), max(z, abs(p))) > BIG)
throw("invalid arguments in rj");
sum = 0.0;
fac = 1.0;
if (p > 0.0) {
nt = x;
yt = y;
yt = z;
pt = p;
} else {
vt = MIN(MIN(x, y), z);
vt = MAX(MAX(x, y), z);
yt = x + y + z - xt - zt;
a = 1.0 / (yt - p);
b = a * (zt - yt) * (yt - xt);
pt = yt + b;
rho = xt * zt / yt;
tau = p - pt / yt;
rcx = rc(rho, tau);
}
do {
sqrt = sqrt(xt);
sqrt = (yt);
sqrt(yt);
sqrt = sqrt(zt);
alpha = SQR(pt * (sqrtty + sqrtz) + sqrtty * sqrtz);
alpha = SQR(pt * (sqrtty + sqrty + sqrtz) + sqrtty * sqrtz);
beta = pt * SQR(pt * (alpha, beta);
sum += fac * rc(alpha, beta);
fac = 0.25 * fac;
xt = 0.25 * (xt + alamb);
yt = 0.25 * (yt + alamb);
zt = 0.25 * (zt + alamb);
pt = 0.25 * (pt + alamb);
ave = 0.2 * (xt + yt + zt + pt + pt);
delx = (ave - xt) / ave;
dely = (ave - yt) / ave;
delz = (ave - zt) / ave;
delp = (ave - pt) / ave;
} while (MAX(MAX(abs(delx), abs(dely)), MAX(abs(delz), abs(delp))) > ERRRTL);
ea = delx * (dely + delz) + dely * delz;
eb = delx * dely * delz;
ec = delp * delp;
ed = ea - 3.0 * ec;
ee = eb + 2.0 * delp * (ea - ec);
ans = 3.0 * sum * fac * (1.0 + ed * (-C1 + C5 * ed - C6 * ee) + eb * (C7 + delp * (-C8 + delp * C4)) + delp * ea * (C2 - delp * C3) - C2 * delp * ec) / (ave * sqrt(ave));
if (p <= 0.0) ans = a * (b * ans + 3.0 * (rcx - rf(xt, yt, zt)));
return ans;
Doub rc(const Doub x, const Doub y) {
// 计算 Carlson 的退化椭圆积分 $R_C(x,y)$。$x$ 必须非负,$y$ 必须非零。
// 若 $y < 0$,则返回柯西主值。
static const Doub ERRRTL = 0.0012, THIRD = 1.0 / 3.0, C1 = 0.3, C2 = 1.0 / 7.0, C3 = 0.375, C4 = 9.0 / 22.0;
static const Doub TINY = 5.0 * numeric_limits<Doub>::min(), BIG = 0.2 * numeric_limits<Doub>::max(), COMP1 = 2.236 / sqrt(TINY), COMP2 = SQR(TINY * BIG) / 25.0;
Doub alamb, ave, s, w, xt, yt;
if (x < 0.0 || y == 0.0 || (x + abs(y)) < TINY || (x + abs(y)) > BIG || (y < -COMP1 && x > 0.0 && x < COMP2))
throw("invalid arguments in rc");
if (y > 0.0) {
xt = x;
yt = y;
w = 1.0;
} else {
xt = x - y;
yt = -y;
w = sqrt(x) / sqrt(xt);
}
do {
alamb = 2.0 * sqrt(xt) * sqrt(yt) + yt;
xt = 0.25 * (xt + alamb);
yt = 0.25 * (yt + alamb);
ave = THIRD * (xt + yt + yt);
s = (yt - ave) / ave;
} while (abs(s) > ERRRTL);
return w * (1.0 + s * s * (C1 + s * (C2 + s * (C3 + s * C4)))) / sqrt(ave);
}
有时你可能希望用勒让德(Legendre)记号表达你的结果。或者,你可能得到以该记号表示的结果,并需要用上述程序计算其数值。在两种记号之间相互转换是很容易的。
第一类勒让德椭圆积分定义为:
第一类完全椭圆积分为:
用 表示为:
第二类勒让德椭圆积分和第二类完全椭圆积分分别为:
最后,第三类勒让德椭圆积分为:
(注意:此处对参数 的符号约定与 Abramowitz 和 Stegun [13] 相反,且他们的 对应于我们的 。)
Doub ellf(const Doub phi, const Doub ak) {
// 使用 Carlson 函数 $R_F$ 计算第一类勒让德椭圆积分 $F(\phi,k)$。
// 参数范围为 $0 \leq \phi \leq \pi/2$,$0 \leq k \sin \phi \leq 1$。
Doub s = sin(phi);
return s * rf(SQR(cos(phi)), (1.0 - s * ak) * (1.0 + s * ak), 1.0);
}
Doub ellpi(const Doub phi, const Doub en, const Doub ak) {
// 使用 Carlson 函数 $R_F$ 和 $R_J$ 计算第三类勒让德椭圆积分 $\Pi(\phi,n,k)$。
// (注意:此处对 $n$ 的符号约定与 Abramowitz 和 Stegun 相反。)
// 参数范围为 $0 \leq \phi \leq \pi/2$,$0 \leq k \sin \phi \leq 1$。
Doub cc, enss, q, s;
s = sin(phi);
enss = en * s * s;
cc = SQR(cos(phi));
q = (1.0 - s * ak) * (1.0 + s * ak);
return s * (rf(cc, q, 1.0) - enss * rj(cc, q, 1.0, 1.0 + enss) / 3.0);
}
Carlson 函数具有齐次性,次数分别为 和 ,因此:
因此,要将 Carlson 函数用勒让德记号表示,只需将前三个参数按升序排列,利用齐次性将第三个参数缩放为 1,然后使用公式 (6.12.19)–(6.12.21)。
6.12.1 雅可比椭圆函数
雅可比椭圆函数 定义如下:考虑椭圆积分而非……
考虑其反函数
等价地,
当 时, 就是 。函数 和 由以下关系定义:
下面给出的例程实际上以 作为输入参数。该例程同时计算三个函数 、 和 ,因为计算全部三个函数并不比仅计算其中一个更困难。关于该方法的描述,参见 [9]。
void sncndn(const Doub u, const Doub emmc, Doub &sn, Doub &cn, Doub &dn) {
// 返回雅可比椭圆函数 sn(u,k_c)、cn(u,k_c) 和 dn(u,k_c)。
// 这里 u = u,而 emmc = k_c^2。
static const Doub CA = 1.0e-8;
bool bo;
Int i, ii, l;
Doub a, b, c, d, emc;
VecDoub em(13), en(13);
emc = emmc;
if (emc != 0.0) {
bo = (emc < 0.0);
if (bo) {
d = 1.0 - emc;
emc = -1.0 / d;
u *= (d = sqrt(d));
}
a = 1.0;
dn = 1.0;
for (i = 0; i < 13; i++) {
l = i;
em[i] = a;
en[i] = (emc = sqrt(emc));
c = 0.5 * (a + emc);
if (abs(a - emc) <= CA * a) break;
emc = a - emc;
a = c;
}
u *= c;
sn = sin(u);
cn = cos(u);
if (sn != 0.0) {
a = cn / sn;
c = a;
for (ii = l; ii >= 0; ii--) {
b = em[ii];
a = c * b;
c = dn * b;
dn = (en[ii] + a) / (b + a);
a = c / b;
}
a = 1.0 / sqrt(c * c + 1.0);
sn = (sn >= 0.0 ? a : -a);
cn = c * sn;
}
if (bo) {
a = dn;
dn = cn;
cn = a;
sn /= d;
}
} else {
cn = 1.0 / cosh(u);
dn = cn;
sn = tanh(u);
}
}
参考文献
Erdélyi, A., Magnus, W., Oberhettinger, F., and Tricomi, F.G. 1953, Higher Transcendental Functions, Vol. II, (New York: McGraw-Hill).[1]
Gradshteyn, I.S., and Ryzhik, I.W. 1980, Table of Integrals, Series, and Products (New York: Academic Press).[2]
Carlson, B.C. 1977, "Elliptic Integrals of the First Kind," SIAM Journal on Mathematical Analysis, vol. 8, pp. 231–242.[3]
Carlson, B.C. 1987, "A Table of Elliptic Integrals of the Second Kind," Mathematics of Computation, vol. 49, pp. 595–606[4]; 1988, "A Table of Elliptic Integrals of the Third Kind," op. cit., vol. 51, pp. 267–280[5]; 1989, "A Table of Elliptic Integrals: Cubic Cases," op. cit., vol. 53, pp. 327–333[6]; 1991, "A Table of Elliptic Integrals: One Quadratic Factor," op. cit., vol. 56, pp. 267–280.[7]
Carlson, B.C., and FitzSimons, J. 2000, "Reduction Theorems for Elliptic Integrands with the Square Root of Two Quadratic Factors," Journal of Computational and Applied Mathematics, vol. 118, pp. 71–85.[8]
Bulirsch, R. 1965, "Numerical Calculation of Elliptic Integrals and Elliptic Functions," Numerische Mathematik, vol. 7, pp. 78–90; 1965, op. cit., vol. 7, pp. 353–354; 1969, op. cit., vol. 13, pp. 305–315.[9]
Carlson, B.C. 1979, "Computing Elliptic Integrals by Duplication," Numerische Mathematik, vol. 33, pp. 1–16.[10]
Carlson, B.C., and Notis, E.M. 1981, "Algorithms for Incomplete Elliptic Integrals," ACM Transactions on Mathematical Software, vol. 7, pp. 398–403.[11]
Carlson, B.C. 1978, "Short Proofs of Three Theorems on Elliptic Integrals," SIAM Journal on Mathematical Analysis, vol. 9, pp. 524–528.[12]
Abramowitz, M., and Stegun, I.A. 1964, Handbook of Mathematical Functions (Washington: National Bureau of Standards); reprinted 1968 (New York: Dover); online at http://www.nr.com/aands, Chapter 17.[13]
Mathews, J., and Walker, R.L. 1970, Mathematical Methods of Physics, 2nd ed. (Reading, MA: W.A. Benjamin/Addison-Wesley), pp. 78–79.
6.13 超几何函数
如 §5.14 中所述,要为复超几何函数 编写一个快速且通用的例程是困难甚至不可能的。该函数定义为超几何级数的解析延拓:
该级数仅在单位圆 内收敛(参见 [1]),但人们对这一函数的兴趣并不局限于该区域。
第 5.14 节讨论了通过在复平面上直接路径积分来计算该函数的方法。此处仅列出由此得到的例程。
函数 hypgeo 的实现非常直接,程序中的注释已对其进行了说明。第 17 章中用于积分微分方程的例程 Odeint 所涉及的机制侵入性极小,甚至无需完全理解:使用 Odeint 仅需一次对构造函数的调用(要求导数例程 Hypperiev 采用规定的格式),随后调用 integrate 方法即可。
当然,当 的值过于接近奇点 1 时,函数 hypgeo 会失效。(若需逼近该奇点或无穷远处的奇点,请使用文献 [1] 中 §15.3 节所述的“线性变换公式”。)在远离 且 取值适中的情况下,积分方程所需的步数往往少得令人惊讶,通常只需六步左右。
hypgeo.h
Complex hypgeo(const Complex &a, const Complex &b, const Complex &c, const Complex &z)
通过在复平面上直接积分超几何方程,计算复参数 和复变量 的复超几何函数 。其分支切割线取为实轴上 的部分。
{
const Doub atol = 1.0e-14, rtol = 1.0e-14;
Complex ans, dz, z0, y[2];
VecDoub yy(4);
if (norm(z) <= 0.25) {
hypser(a, b, c, z, ans, y[1]);
return ans;
}
// ... 或者选择路径积分的起点。
else if (real(z) < 0.0) z0 = Complex(-0.5, 0.0);
else if (real(z) <= 1.0) z0 = Complex(0.5, 0.0);
else z0 = Complex(0.0, imag(z) >= 0.0 ? 0.5 : -0.5);
dz = z - z0;
hyper(a, b, c, z0, y[0], y[1]);
yy[0] = real(y[0]);
yy[1] = imag(y[0]);
yy[2] = real(y[1]);
yy[3] = imag(y[1]);
Hypervisor d(a, b, c, z0, dz);
Output out;
Odeint<StepperBS<Hypervisor>> ode(yy, 0.0, 1.0, atol, rtol, 0.1, 0.0, out, d);
// Odeint 的参数依次为:自变量向量、因变量的起始值和终止值、精度参数、步长的初始猜测值、最小步长,以及输出对象和导数对象的名称。
// 积分由 Bulirsch-Stoer 步进例程执行。
ode.integrate();
y[0] = Complex(yy[0], yy[1]);
return y[0];
}
void hypser(const Complex &a, const Complex &b, const Complex &c, const Complex &z, Complex &series, Complex &deriv)
返回超几何级数 及其导数,迭代至机器精度。当 时,收敛速度相当快。
{
deriv = 0.0;
Complex fac = 1.0;
Complex temp = fac;
Complex aa = a;
Complex bb = b;
Complex cc = c;
for (Int n = 1; n <= 1000; n++) {
fac *= ((aa * bb) / cc);
deriv += fac;
fac *= ((1.0 / n) * z);
series = temp + fac;
if (series == temp) return;
temp = series;
aa += 1.0;
bb += 1.0;
cc += 1.0;
}
throw("convergence failure in hypser");
}
struct Hypervisor {
// 用于计算超几何方程的导数;参见正文公式 (5.14.4)。
Complex a, b, c, z0, dz;
Hypervisor(const Complex &aa, const Complex &bb,
const Complex &cc, const Complex &z00,
const Complex &ddz) : a(aa), b(bb), c(cc), z0(z00), dz(ddz) {}
void operator()(const Doub s, VecDoub_I &yy, VecDoub_O &dyyds) {
Complex z, y[2], dyds[2];
y[0] = Complex(yy[0], yy[1]);
y[1] = Complex(yy[2], yy[3]);
z = z0 + s * dz;
dyds[0] = y[1] * dz;
dyds[1] = (a * b * y[0] - (c - (a + b + 1.0) * z) * y[1]) * dz / (z * (1.0 - z));
dyyds[0] = real(dyds[0]);
dyyds[1] = imag(dyds[0]);
dyyds[2] = real(dyds[1]);
dyyds[3] = imag(dyds[1]);
}
};
参考文献
Abramowitz, M., and Stegun, I.A. 1964, Handbook of Mathematical Functions (Washington: National Bureau of Standards); 1968 年重印 (New York: Dover); 在线版见 http://www.nr.com/aands。[1]
6.14 统计函数
某些特殊函数因其与常见的一元统计分布(即单变量的概率密度函数)相关而被频繁使用。本节以统一的方式综述若干此类常见分布,针对每种分布,均提供计算概率密度函数 、累积分布函数(cdf,记为 )以及累积分布函数的反函数 的例程。后一函数用于在显著性检验中求取与指定百分位点或分位数对应的 值,例如 0.5%、5%、95% 或 99.5% 分位点。
本节重点在于定义和计算这些统计函数。§7.3 节讨论了如何从本节所述分布中生成随机偏差,与本节内容密切相关。至于这些分布在统计检验中的实际应用,则留待第 14 章讨论。
6.14.1 正态(高斯)分布
若 服从均值为 、标准差为 的正态分布,则记为
其中 为概率密度函数。注意本节中符号“”的特殊用法,可读作“服从某分布”。该分布的方差显然为 。
累积分布函数表示取值 的概率。对于正态分布,其可用互补误差函数表示为
因此,cdf 的反函数可通过 erfc 的反函数计算:
以下结构体实现了上述关系。
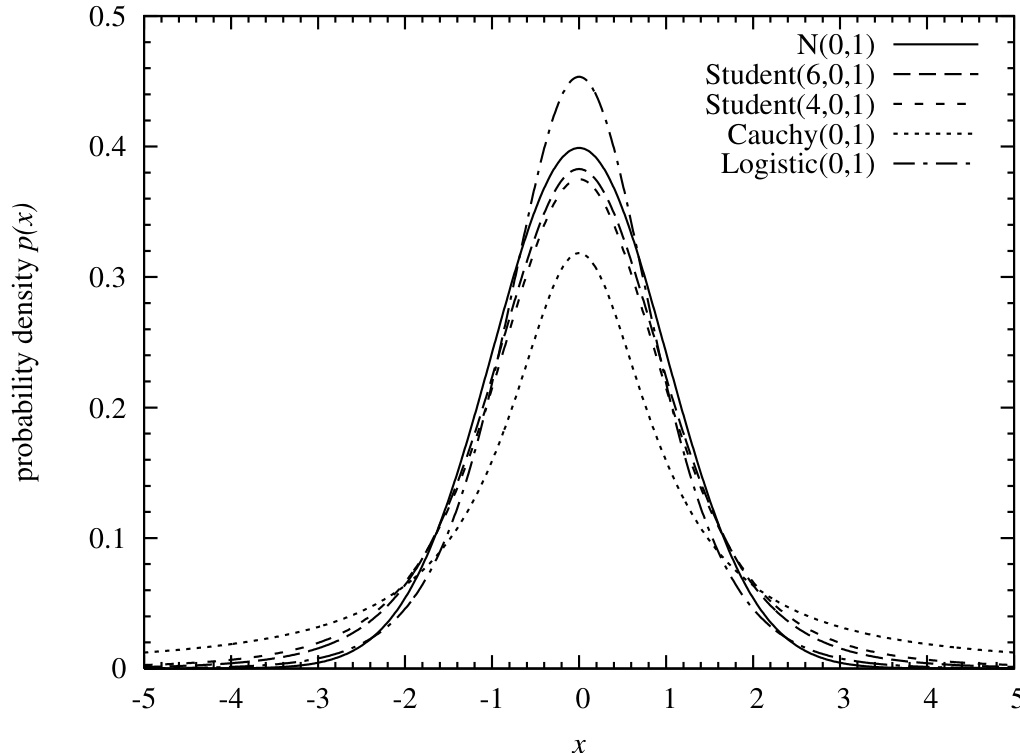
图 6.14.1. 实轴上对称且中心峰值的分布示例。这些分布均可作为正态分布的替代,用于近似或稳健估计等应用。它们的主要区别在于尾部衰减速率。
struct Normaldist : Erf {
// 正态分布,继承自误差函数 Erf。
Doub mu, sig;
Normaldist(Doub mmu = 0., Doub ssig = 1.) : mu(mmu), sig(ssig) {
// 构造函数。用 $\mu$ 和 $\sigma$ 初始化。无参默认构造为 N(0,1)。
if (sig <= 0.) throw("bad sig in Normaldist");
}
Doub p(Doub x) {
// 返回概率密度函数。
return (0.398942280401432678 / sig) * exp(-0.5 * SQR((x - mu) / sig));
}
Doub cdf(Doub x) {
// 返回累积分布函数。
return 0.5 * erfc(-0.707106781186547524 * (x - mu) / sig);
}
Doub invcdf(Doub p) {
// 返回累积分布函数的反函数。
if (p <= 0. || p >= 1.) throw("bad p in Normaldist");
return -1.41421356237309505 * sig * inverfc(2. * p) + mu;
}
};
本节所有分布均遵循上述代码的约定:分布的参数(此处为 和 )由构造函数设定,成员函数按需引用。密度函数恒为 p(),cdf 为 cdf(),cdf 的反函数为 invcdf()。通常我们会对概率函数的参数进行有效性检查,因为许多程序错误会表现为概率值超出 [0, 1] 范围等问题。
6.14.2 柯西分布
与正态分布类似,柯西分布也是一种中心峰值对称的分布,具有一个指定其中心位置的参数 和一个指定其宽度的参数 。然而,与正态分布不同的是,柯西分布在无穷远处的尾部衰减非常缓慢,按 的速率衰减,以至于高于零阶矩(即曲线下面积)的矩甚至不存在。因此,严格来说,参数 并不是均值,参数 在技术上也不是标准差。但这两个参数可以作为中心位置和宽度的度量,替代这些矩的作用。
其定义的概率密度函数为:
若 Cauchy(0,1),则 Cauchy(0,1),且 Cauchy()。
累积分布函数(cdf)为:
逆累积分布函数为:
图 6.14.1 展示了柯西分布 Cauchy(0, 1) 与正态分布 N(0, 1) 的对比,以及下文将讨论的几种其他形状相似的分布。
柯西分布有时也被称为洛伦兹分布。
// distributions.h
struct Cauchydist {
// 柯西分布。
Doub mu, sig;
Cauchydist(Doub mmu = 0., Doub ssig = 1.) : mu(mmu), sig(ssig) {
// 构造函数。用 $\mu$ 和 $\sigma$ 初始化。无参数时默认为 Cauchy(0, 1)。
if (sig <= 0.) throw("bad sig in Cauchydist");
}
Doub p(Doub x) {
// 返回概率密度函数。
return 0.318309886183790671/(sig*(1.+SQR((x-mu)/sig)));
}
Doub cdf(Doub x) {
// 返回累积分布函数。
return 0.5+0.318309886183790671*atan2(x-mu,sig);
}
Doub invcdf(Doub p) {
// 返回逆累积分布函数。
if (p <= 0. || p >= 1.) throw("bad p in Cauchydist");
return mu + sig*tan(3.14159265358979324*(p-0.5));
}
};
6.14.3 学生 t 分布
柯西分布的一个推广是学生 t 分布,以 20 世纪初的统计学家 William Gosset 命名,他以“Student”为笔名发表论文,因为其雇主 Guinness 酿酒厂要求他使用化名。与柯西分布类似,学生 t 分布在无穷远处也具有幂律尾部,但它多了一个参数 ,用于指定尾部衰减速率,即按 衰减。当 为整数时,包括零阶矩在内的收敛矩的个数即为 。
其定义的概率密度函数(习惯上用变量 而非 表示)为:
当 时,即得到柯西分布;而在 的极限情况下,则得到正态分布。在计算机出现之前,这是各种正态分布近似方法的基础,如今这些方法大多已不再使用。图 6.14.1 展示了 (即柯西分布)、 和 时的学生 t 分布示例,可以看出其向正态分布逼近的趋势。
Student(, , ) 的均值(由对称性)为 。其方差并非 ,而是:
关于更高阶矩及其他性质,参见 [1]。
累积分布函数由不完全贝塔函数给出。若令
则
逆累积分布函数由逆不完全贝塔函数给出(具体形式见下文代码)。
在实际应用中,上述形式的学生 t 分布累积分布函数很少直接使用,因为大多数使用学生 t 分布的统计检验都是双侧的。通常,双尾函数 仅针对 且 的情况定义为:
其中 如上所述。统计量 常用于检验两个观测分布是否具有相同的均值。下文代码实现了公式 (6.14.10) 和 (6.14.11) 及其逆函数。
struct Studenttdist : Beta {
// 学生 t 分布,派生自贝塔函数 Beta。
Doub nu, mu, sig, np, fac;
Studenttdist(Doub nnu, Doub mmu = 0., Doub ssig = 1.)
: nu(nnu), mu(mmu), sig(ssig) {
// 构造函数。用 $\nu$、$\mu$ 和 $\sigma$ 初始化。单参数默认为 Student($\nu$, 0, 1)。
if (sig <= 0. || nu <= 0.) throw("bad sig, nu in Studenttdist");
np = 0.5*(nu + 1);
fac = gammln(np)-gammln(0.5*nu);
}
Doub p(Doub t) {
// 返回概率密度函数。
return exp(-np*log(1.+SQR((t-mu)/sig)/nu)+fac)
/(sqrt(3.14159265358979324*nu)*sig);
}
Doub cdf(Doub t) {
// 返回累积分布函数。
Doub p = 0.5*beta1(0.5*nu, 0.5, nu/(nu+SQR((t-mu)/sig)));
if (t >= mu) return 1. - p;
else return p;
}
Doub invcdf(Doub p) {
// 返回逆累积分布函数。
if (p <= 0. || p >= 1.) throw("bad p in Studenttdist");
Doub x = invbeta1(2.*MIN(p,1.-p), 0.5*nu, 0.5);
x = sig*sqrt(nu*(1.-x)/x);
return (p >= 0.5? mu+x : mu-x);
}
Doub aa(Doub t) {
// 返回双尾累积分布函数 $A(t|\nu)$。
if (t < 0.) throw("bad t in Studenttdist");
return 1.-beta1(0.5*nu, 0.5, nu/(nu+SQR(t)));
}
Doub invaa(Doub p) {
// 返回逆函数,即满足 $p = A(t|\nu)$ 的 $t$。
if (p < 0. || p >= 1.) throw("bad p in Studenttdist");
Doub x = invbeta1(1.-p, 0.5*nu, 0.5);
return sqrt(nu*(1.-x)/x);
}
};
6.14.4 Logistic 分布
Logistic 分布是另一种对称、中心尖峰的分布,可以替代正态分布使用。其尾部呈指数衰减,但仍比正态分布的“平方指数”衰减得慢得多。
其定义的概率密度函数为:
这三种形式在代数上是等价的,但为了避免溢出,对正的 值应使用负指数形式,对负的 值应使用正指数形式。
该分布(6.14.12)的方差为 。由于通常希望参数 和 具有均值和标准差的传统含义,因此常用标准化的 Logistic 分布替代公式(6.14.12):
这等价于使用正负指数形式的表达式(见下文代码)。
累积分布函数(cdf)为:
逆累积分布函数为:
struct Logisticdist {
// Logistic 分布。
Doub mu, sig;
Logisticdist(Doub mmu = 0., Doub ssig = 1.) : mu(mmu), sig(ssig) {
// 构造函数。用 $\mu$ 和 $\sigma$ 初始化。无参数时默认为 Logistic(0,1)。
if (sig <= 0.) throw("bad sig in Logisticdist");
}
Doub p(Doub x) {
// 返回概率密度函数。
Doub e = exp(-abs(1.81379936423421785*(x-mu)/sig));
return 1.81379936423421785*e/(sig*SQR(1.+e));
}
Doub cdf(Doub x) {
// 返回累积分布函数。
Doub e = exp(-abs(1.81379936423421785*(x-mu)/sig));
if (x >= mu) return 1./(1.+e);
else return e/(1.+e);
}
Doub invcdf(Doub p) {
// 返回逆累积分布函数。
if (p <= 0. || p >= 1.) throw("bad p in Logisticdist");
return mu + 0.551328895421792049*sig*log(p/(1.-p));
}
};
Logistic 分布与 logit 变换密切相关。logit 变换通过以下关系将开区间 映射到实数轴 :
在统计学家依赖查表和计算尺的时代,logit 变换被用来将区间上的过程近似为实数轴上解析上更简单的过程。区间上的均匀分布经 logit 变换后,会映射为实数轴上的 Logistic 分布。如今,计算机可以直接计算区间上的分布(例如 Beta 分布),这种动机已不复存在。
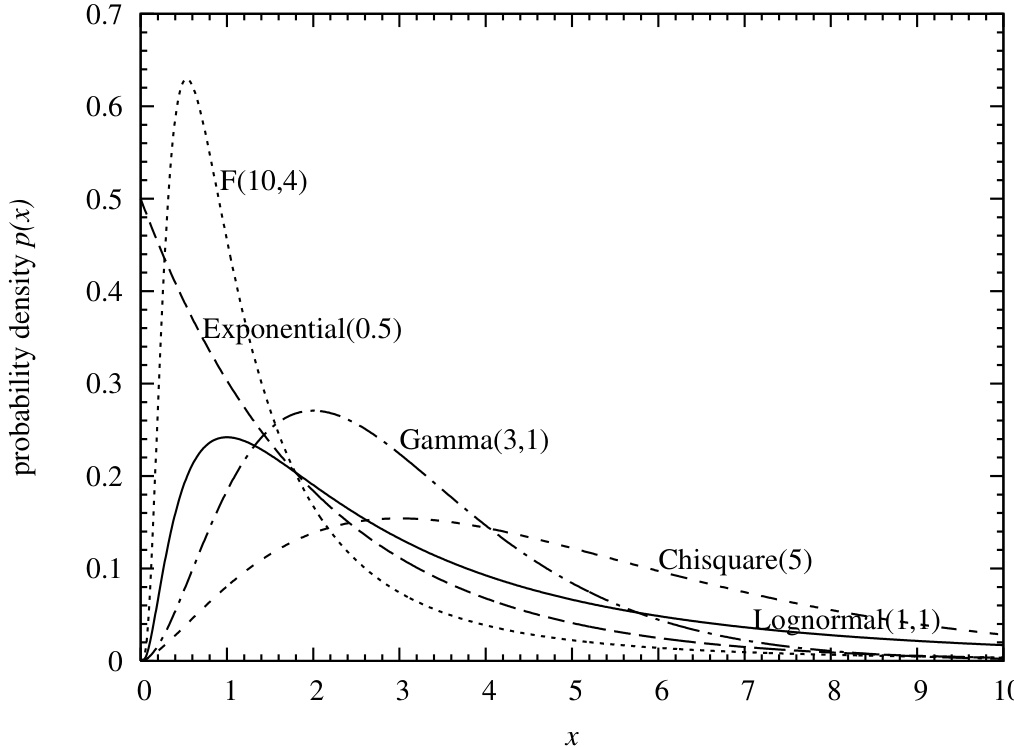
图 6.14.2. 半直线 上常见分布的示例
另一个“亲戚”是 Logistic 方程:
这是一个描述某量 增长的微分方程:初始阶段呈指数增长,但渐近地趋近于某个值 。该方程的解(在缩放下)与 Logistic 分布的累积分布函数完全相同。
6.14.5 指数分布
现在我们转向定义在正实轴 上的常见分布函数。图 6.14.2 展示了我们将讨论的几种分布的示例。其中指数分布最为简单。它有一个参数 ,可控制其宽度(成反比关系),但其众数始终位于零点:
指数分布的均值和标准差均为 ,中位数为 。参考文献 [1] 对指数分布的讨论之详尽,远超你的想象。
struct Expondist {
// 指数分布。
Doub bet;
Expondist(Doub bbet) : bet(bbet) {
// 构造函数。用 $\beta$ 初始化。
if (bet <= 0.) throw("bad bet in Expondist");
}
Doub p(Doub x) {
// 返回概率密度函数。
if (x < 0.) throw("bad x in Expondist");
return bet*exp(-bet*x);
}
Doub cdf(Doub x) {
// 返回累积分布函数。
if (x < 0.) throw("bad x in Expondist");
return 1.-exp(-bet*x);
}
Doub invcdf(Doub p) {
// 返回逆累积分布函数。
if (p < 0. || p >= 1.) throw("bad p in Expondist");
return -log(1.-p)/bet;
}
};
6.14.6 Weibull 分布
Weibull 分布以一种在风险、生存或可靠性研究中常用的方式推广了指数分布。当某物品的寿命(失效时间)服从指数分布时,若该物品尚未失效,则其单位时间内失效的概率是恒定的。也就是说,
指数分布寿命的物品不会老化;它们只是不断地掷相同的骰子,直到某一天“轮到”它们失效为止。然而,在许多其他情况下,人们观察到物品的危险率(如上所定义)会随时间变化,例如遵循幂律:
由此产生的分布是威布尔分布(Weibull distribution),以瑞典物理学家瓦洛迪·威布尔(Waloddi Weibull)命名,他早在1939年就已使用该分布。当 时,危险率随时间增加,这适用于会逐渐磨损的部件;当 时,危险率随时间减小,这适用于经历“早期失效”(infant mortality)的部件。
我们称
其概率密度函数为
累积分布函数(cdf)为
逆累积分布函数为
当 时,该分布在 处具有一个无穷大(但可积)的尖点,并且单调递减。指数分布对应于 的情形。当 时,分布在 处为零,并在 处取得唯一极大值。
其均值和方差分别为
经正确归一化后,式 (6.14.22) 变为
6.14.7 对数正态分布(Lognormal Distribution)
许多定义在正实数轴上的过程,自然地可以用对数坐标轴(即 轴,其中 )上的正态分布来近似。一个简单但重要的例子是乘法随机游走:它从某个正初值 开始,然后通过如下递推关系生成新值:
其中 是某个小的固定常数。
这些考虑引出了如下定义:
或等价地定义为
注意指数函数前必须包含额外的因子 :所谓“正态”的密度实际上是 。
虽然 和 是 空间中的均值和标准差,但它们并不是 空间中的均值和标准差。实际上,
其累积分布函数为
累积分布函数(CDF)的反函数涉及互补误差函数的反函数,
struct Lognormaldist : Erf {
// 对数正态分布,由误差函数 Erf 派生。
Doub mu, sig;
Lognormaldist(Doub mmu = 0., Doub ssig = 1.) : mu(mmu), sig(ssig) {
if (sig <= 0.) throw("bad sig in Lognormaldist");
}
Doub p(Doub x) {
// 返回概率密度函数。
if (x < 0.) throw("bad x in Lognormaldist");
if (x == 0.) return 0;
return (0.398942280401432678/(sig*x))*exp(-0.5*SQR((log(x)-mu)/sig));
}
Doub cdf(Doub x) {
// 返回累积分布函数。
if (x < 0.) throw("bad x in Lognormaldist");
if (x == 0.) return 0;
return 0.5*erfc(-0.707106781186547524*(log(x)-mu)/sig);
}
Doub invcdf(Doub p) {
// 返回累积分布函数的反函数。
if (p <= 0. || p >= 1.) throw("bad p in Lognormaldist");
return exp(-1.41421356237309505*sig*inverfc(2.*p)+mu);
}
};
类似于式 (6.14.29) 的乘性随机游走和对数正态分布是有效市场经济学理论的关键组成部分,由此导出了(除其他众多结果外)著名的 Black-Scholes 公式,用于描述经过一段时间 后投资价格的概率分布。Black-Scholes 推导中的一个关键点隐含在式 (6.14.32) 中:如果一项投资的平均收益率为零(在零风险极限下可能成立),那么其价格不能简单地表现为一个具有固定 和不断增大的 的展宽对数正态分布,因为其期望值会发散至无穷大!因此,实际的 Black-Scholes 公式同时定义了 如何随时间增长(基本上按 增长)以及 如何相应地随时间减小,以保持整体均值可控。Black-Scholes 公式的简化形式可写作
其中 是股票在时间 的价格, 是其预期(年化)收益率,而 现在被重新定义为股票的(年化)波动率。波动率的定义是:对于较小的 ,股票价格的相对方差为 。你可以验证,若 ,则式 (6.14.35) 对所有 都满足期望值 。一个很好的参考文献是 [3]。
6.14.8 卡方分布
卡方(或 )分布具有一个参数 ,该参数同时控制其峰值的位置和宽度。在大多数应用中, 为整数,并被称为自由度(参见 §14.3)。
其定义的概率密度为
此处我们写出微分 仅是为了强调 (而非 )应被视为自变量。
其均值和方差分别为
当 时,分布具有唯一众数,位于 。
卡方分布实际上是下文所述伽马分布的一个特例,因此其累积分布函数(CDF)可用不完全伽马函数 表示:
人们也经常使用 CDF 的补函数,它既可通过不完全伽马函数 计算,也可通过其补函数 计算(当 非常接近 1 时,后者通常更精确):
CDF 的反函数可通过 关于其第二个参数的反函数表示,此处记为 :
struct Chisqdist : Gamma {
// $\chi^{2}$ 分布,由伽马函数 Gamma 派生。
Doub nu, fac;
Chisqdist(Doub nnu) : nu(nnu) {
// 构造函数。用 $\nu$ 初始化。
if (nu <= 0.) throw("bad nu in Chisqdist");
fac = 0.693147180559945309*(0.5*nu)+gammln(0.5*nu);
}
Doub p(Doub x2) {
// 返回概率密度函数。
if (x2 <= 0.) throw("bad x2 in Chisqdist");
return exp(-0.5*(x2-(nu-2.)*log(x2))-fac);
}
Doub cdf(Doub x2) {
// 返回累积分布函数。
if (x2 < 0.) throw("bad x2 in Chisqdist");
return gammp(0.5*nu,0.5*x2);
}
Doub invcdf(Doub p) {
// 返回累积分布函数的反函数。
if (p < 0. || p >= 1.) throw("bad p in Chisqdist");
return 2.*invamp(p,0.5*nu);
}
};
6.14.9 伽马分布
伽马分布定义为
指数分布是 时的特例。卡方分布则是 且 时的特例。
其均值和方差分别为
当 时,分布具有唯一众数,位于 。
显然,其累积分布函数(CDF)即为不完全伽马函数。
而其逆累积分布函数(inverse cdf)则通过 对其第二个参数的逆函数给出:
struct Gammadist : Gamma {
// Gamma distribution, derived from the gamma function Gamma.
Doub alpha, bet, fac;
Gammadist(Doub aalph, Doub bbet = 1.) : alpha(aalph), bet(bbet) {
// Constructor. Initialize with α and β.
if (alpha <= 0. || bet <= 0.) throw("bad alpha,bet in Gammadist");
fac = alpha * log(bet) - gammln(alpha);
}
Doub p(Doub x) {
// Return probability density function.
if (x <= 0.) throw("bad x in Gammadist");
return exp(-bet * x + (alpha - 1.) * log(x) + fac);
}
Doub cdf(Doub x) {
// Return cumulative distribution function.
if (x < 0.) throw("bad x in Gammadist");
return gammp(alpha, bet * x);
}
Doub invcdf(Doub p) {
// Return inverse cumulative distribution function.
if (p < 0. || p >= 1.) throw("bad p in Gammadist");
return invgammp(p, alpha) / bet;
}
};
6.14.10 F 分布
分布由两个正数参数 和 参数化,通常(但不总是)为整数。
其定义的概率密度函数为:
其中 表示 beta 函数。其均值和方差分别为:
当 时,分布具有唯一的众数(mode):
对于固定的 ,若 ,则 分布趋近于卡方分布,即:
其中符号 “” 表示 “分布相同”。
分布的累积分布函数(cdf)可通过不完全 beta 函数 表示为:
而其逆累积分布函数则通过 对其下标参数的逆函数给出:
分布的一个常见用途是检验两个观测样本是否具有相同的方差。
struct Fdist : Beta {
// F distribution, derived from the beta function Beta.
Doub nu1, nu2;
Doub fac;
Fdist(Doub nuu1, Doub nnu2) : nu1(nuu1), nu2(nnu2) {
// Constructor. Initialize with ν₁ and ν₂.
if (nu1 <= 0. || nu2 <= 0.) throw("bad nu1,nu2 in Fdist");
fac = 0.5 * (nu1 * log(nu1) + nu2 * log(nu2)) + gammln(0.5 * (nu1 + nu2))
- gammln(0.5 * nu1) - gammln(0.5 * nu2);
}
Doub p(Doub f) {
// Return probability density function.
if (f <= 0.) throw("bad f in Fdist");
return exp((0.5 * nu1 - 1.) * log(f) - 0.5 * (nu1 + nu2) * log(nu2 + nu1 * f) + fac);
}
Doub cdf(Doub f) {
// Return cumulative distribution function.
if (f < 0.) throw("bad f in Fdist");
return betai(0.5 * nu1, 0.5 * nu2, nu1 * f / (nu2 + nu1 * f));
}
Doub invcdf(Doub p) {
// Return inverse cumulative distribution function.
if (p <= 0. || p >= 1.) throw("bad p in Fdist");
Doub x = invbeta1(p, 0.5 * nu1, 0.5 * nu2);
return nu2 * x / (nu1 * (1. - x));
}
};
6.14.11 Beta 分布
Beta 分布定义在单位区间 上:
其均值和方差分别为:
当 且 时,分布具有唯一的众数 。当 且 时,分布呈“U 形”,在该值处取得最小值。其他情况下,分布既无最大值也无最小值。
当 固定而 时,Beta 分布的所有概率质量向 集中,其密度函数趋近于 Gamma 分布。更精确地:
累积分布函数(cdf)是不完全贝塔函数:
而其反函数则通过 对下标参数的反函数给出:
struct Betadist : Beta {
// Beta 分布,由贝塔函数 Beta 推导而来。
Doub alpha, bet, fac;
Betadist(Doub aalph, Doub bbet) : alpha(aalph), bet(bbet) {
// 构造函数。用 α 和 β 初始化。
if (alpha <= 0. || bet <= 0.) throw("bad alpha,bet in Betadist");
fac = gammln(alpha+bet)-gammln(alpha)-gammln(bet);
}
Doub p(Doub x) {
// 返回概率密度函数。
if (x <= 0. || x >= 1.) throw("bad x in Betadist");
return exp((alpha-1.)*log(x)+(bet-1.)*log(1.-x)+fac);
}
Doub cdf(Doub x) {
// 返回累积分布函数。
if (x < 0. || x > 1.) throw("bad x in Betadist");
return betai(alpha,bet,x);
}
Doub invcdf(Doub p) {
// 返回反累积分布函数。
if (p < 0. || p > 1.) throw("bad p in Betadist");
return invbetai(p,alpha,bet);
}
};
6.14.12 柯尔莫哥洛夫-斯米尔诺夫分布(Kolmogorov-Smirnov Distribution)
柯尔莫哥洛夫-斯米尔诺夫(KS)分布定义于正数 ,是 §14.3 中讨论的重要统计检验的关键。其概率密度函数并不直接用于该检验,几乎从未被显式写出。通常需要计算的是累积分布函数(cdf),记为 ,或其补函数 。
cdf 由以下级数定义:
或等价地(虽然并不显然)由以下级数定义:
其极限值符合对名为“P”和“Q”的 cdf 的预期:
上述两个级数(6.14.56)和(6.14.57)对所有 均收敛。此外,对任意 ,总有一个级数收敛极快,只需不超过三项即可达到 IEEE 双精度的相对精度。在 处切换使用两个级数是一个较好的选择。这使得 KS 函数可通过单次指数运算和少量算术运算计算(见下文代码)。
求反函数 和 (即由 或 值返回 值)则稍复杂一些。对于 (即 ),基于(6.14.56)的迭代效果良好:
当 时,只需取 的前两项幂即可。
对于更大的 值(即 ),所需 的幂次数迅速变得过多。一种有效的方法是将(6.14.57)改写为:
若能对 给出足够好的初始猜测,即可通过 Halley 方法的变体求解(6.14.60)中的第一个方程:在(6.14.60)右侧使用上一次迭代的 值,仅对 项使用 Halley 方法,从而使一阶和二阶导数成为解析形式的简单函数。
一个良好的初始猜测是使用 的反函数(即 §6.11 中的 invxlogx 函数),其参数为 。在 invxlogx 函数和 Halley 循环中的迭代次数均不超过六次,通常更少。KS 函数及其反函数的代码如下。
struct KSDist {
// 柯尔莫哥洛夫-斯米尔诺夫累积分布函数及其反函数。
Doub pks(Doub z) {
// 返回累积分布函数。
if (z < 0.) throw("bad z in KSDist");
if (z == 0.) return 0.;
if (z < 1.18) {
Doub y = exp(-1.23370055013616983/SQR(z));
return 2.25675833419102515*sqrt(-log(y))
*(y + pow(y,9) + pow(y,25) + pow(y,49));
} else {
Doub x = exp(-2.*SQR(z));
return 1. - 2.*(x - pow(x,4) + pow(x,9));
}
}
Doub qks(Doub z) {
// 返回互补累积分布函数。
if (z < 0.) throw("bad z in KSDist");
if (z == 0.) return 1.;
if (z < 1.18) return 1.-pks(z);
Doub x = exp(-2.*SQR(z));
return 2.*(x - pow(x,4) + pow(x,9));
}
Doub invqks(Doub q) {
// 返回互补累积分布函数的反函数。
Doub y, logy, yp, x, xp, ff, u, t;
if (q <= 0. || q > 1.) throw("bad q in KSDist");
if (q == 1.) return 0.;
if (q > 0.3) {
Doub f = -0.392699081698724155*SQR(1.-q);
y = invxlogx(f); // 初始猜测。
do {
yp = y;
logy = log(y);
ff = f/SQR(1.+ pow(y,4)+ pow(y,12));
u = (y*logy-ff)/(1.+logy); // 牛顿法修正。
y = y - (t=u/MAX(0.5,1.-0.5*u/(y*(1.+logy)))); // Halley 方法。
} while (abs(t/y)>1.e-15);
return 1.57079632679489662/sqrt(-log(y));
} else {
Doub x = 0.03;
do {
xp = x;
x = 0.5*q+pow(x,4)-pow(x,9);
if (x > 0.06) x += pow(x,16)-pow(x,25);
} while (abs((x-xp)/x)>1.e-15);
return sqrt(-0.5*log(x));
}
}
Doub invpks(Doub p) { return invqks(1.-p); } // 返回累积分布函数的反函数。
};
6.14.13 泊松分布(Poisson Distribution)
泊松分布由泊松于 1837 年推导得出。它适用于离散且互不相关的事件以单位时间内的某个平均速率发生的过程。对于给定时间段,若 是事件的平均期望次数,则恰好观测到 个事件()的概率分布可写为:
显然 ,因为(6.14.61)中与 相关的因子正是 的级数展开。
泊松分布(Poisson())的均值和方差均为 。其众数唯一,位于 ,即 向下取整后的整数值。
泊松分布的累积分布函数(cdf)可用不完全伽马函数 表示:
由于 是离散的, 与 显然不同,后者由下式给出:
一些特定取值如下:
涉及不完全伽马函数 和 的其他关系式包括:
由于 的离散性,cdf 的反函数需谨慎定义:给定一个值 ,我们定义 为满足下式的整数:
为简洁起见,下面的代码在实现时稍作放宽,允许右侧的 变为 。如果你提供的 值恰好等于某个 ,则需要同时检查返回的 和 。(对于像 0.95、0.99 这类“规整”的 值,这种情况基本上不会发生。)
struct Poissondist : Gamma {
// 泊松分布,由伽马函数 Gamma 派生。
Doub lam;
Poissondist(Doub llam) : lam(llam) {
// 构造函数。用 $\lambda$ 初始化。
if (lam <= 0.) throw("bad lam in Poissondist");
}
Doub p(Int n) {
// 返回概率密度函数。
if (n < 0) throw("bad n in Poissondist");
return exp(-lam + n*log(lam) - gammln(n+1));
}
Doub cdf(Int n) {
// 返回累积分布函数。
if (n < 0) throw("bad n in Poissondist");
if (n == 0) return 0;
return gammq((Doub)n, lam);
}
Int invcdf(Doub p) {
// 给定参数 $P$,返回整数 $n$,使得 $P(<n) \leq P \leq P(<n+1)$。
Int n, nl, nu, inc = 1;
if (p <= 0. || p >= 1.) throw("bad p in Poissondist");
if (p < exp(-lam)) return 0;
n = (Int)MAX(sqrt(lam), 5);
if (p < cdf(n)) {
do {
n = MAX(n - inc, 0);
inc *= 2;
} while (p < cdf(n));
nl = n; nu = n + inc / 2;
} else {
do {
n += inc;
inc *= 2;
} while (p > cdf(n));
nu = n; nl = n - inc / 2;
}
while (nu - nl > 1) {
n = (nl + nu) / 2;
if (p < cdf(n)) nu = n;
else nl = n;
}
return nl;
}
};
6.14.14 二项分布
与泊松分布类似,二项分布也是定义在 上的离散分布。它有两个参数:,即“样本大小”或 可取非零值的最大值;以及 ,即“事件概率”(注意不要与 ,即特定 值的概率混淆)。我们记作:
其中 当然就是二项式系数。
其均值和方差分别为:
分布具有唯一的众数,该众数 满足:
当且仅当 时,分布是对称的;否则,若 ,分布正偏斜;若 ,则负偏斜。更多性质参见 [2]。
当 、 且 保持有限时,二项分布趋近于泊松分布。更精确地:
二项分布的累积分布函数(cdf)可通过不完全贝塔函数 计算:
因此我们也有(与泊松分布类似):
一些特定取值为:
逆累积分布函数(inverse cdf)的定义与上文泊松分布的情形完全相同,并附有相同的关于代码实现的小警告。
struct Binomialdist : Beta {
// 二项分布,由 Beta 函数派生而来。
Int n;
Doub pe, fac;
Binomialdist(Int nn, Doub ppe) : n(nn), pe(ppe) {
// 构造函数。用 $n$(样本大小)和 $p$(事件概率)进行初始化。
if (n <= 0 || pe <= 0. || pe >= 1.) throw("bad args in Binomialdist");
fac = gammln(n+1);
}
Doub p(Int k) {
// 返回概率密度函数。
if (k < 0) throw("bad k in Binomialdist");
if (k > n) return 0;
return exp(k*log(pe) + (n-k)*log(1.-pe)
+ fac - gammln(k+1) - gammln(n-k+1));
}
Doub cdf(Int k) {
// 返回累积分布函数。
if (k < 0) throw("bad k in Binomialdist");
if (k == 0) return 0;
if (k > n) return 1;
return 1. - betai((Doub)k, n-k+1., pe);
}
Int invcdf(Doub p) {
// 给定参数 $P$,返回整数 $n$,使得 $P(<n) \leq P \leq P(<n+1)$。
Int k, kl, ku, inc = 1;
if (p <= 0. || p >= 1.) throw("bad p in Binomialdist");
k = MAX(0, MIN(n, (Int)(n*pe)));
if (p < cdf(k)) {
do {
k = MAX(k - inc, 0);
inc *= 2;
} while (p < cdf(k));
kl = k; ku = k + inc / 2;
} else {
do {
k = MIN(k + inc, n + 1);
inc *= 2;
} while (p > cdf(k));
ku = k; kl = k - inc / 2;
}
while (ku - kl > 1) {
k = (kl + ku) / 2;
if (p < cdf(k)) ku = k;
else kl = k;
}
return kl;
}
};
参考文献
Johnson, N.L. and Kotz, S. 1970, Continuous Univariate Distributions, 2 vols. (Boston: Houghton Mifflin).[1]
Johnson, N.L. and Kotz, S. 1969, Discrete Distributions (Boston: Houghton Mifflin).[2]
Gelman, A., Carlin, J.B., Stern, H.S., and Rubin, D.B. 2003, Bayesian Data Analysis, 2nd ed. (Boca Raton, FL: Chapman & Hall/CRC), Appendix A.
Lyuu, Y-D. 2002, Financial Engineering and Computation (Cambridge, UK: Cambridge University Press).[3]