数值计算相关论文&书籍中文翻译

2.0 引言

线性代数中最基本的任务，或许也是整个科学计算中最基本的任务，就是求解一组线性代数方程中的未知数。一般来说，一组线性代数方程具有如下形式：

$$\begin{array}{rlr}& & a_{00}{x}_0+a_{01}{x}_1+a_{02}{x}_2+\cdots +a_{0,N-1}{x}_{N-1}=b_0\\ & & a_{10}{x}_0+a_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1,N-1}{x}_{N-1}=b_1\\ & & a_{20}{x}_0+a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2,N-1}{x}_{N-1}=b_2\\ & & \cdots \\ & & \cdots \\ & & a_{M-1,0}{x}_0+a_{M-1,1}{x}_1+\cdots +a_{M-1,N-1}{x}_{N-1}=b_{M-1}\end{array}$$

这里，$N$ 个未知数 $x_j$（$j=0,1,\dots ,N-1$）由 $M$ 个方程关联起来。系数 $a_{ij}$（其中 $i=0,1,\dots ,M-1$，$j=0,1,\dots ,N-1$）是已知的数值，右侧的量 $b_i$（$i=0,1,\dots ,M-1$）也是已知的。

若 $N=M$，则方程个数与未知数个数相等，此时很可能存在唯一解 $\{x_j\}$。否则，若 $N\ne M$，情况会更加有趣；我们将在下文进一步讨论。

若将系数 $a_{ij}$ 写成一个矩阵，将右侧的 $b_i$ 写成一个列向量：

$$\mathbf{A}=\left[\begin{array}{llll}{a}_{00}& a_{01}& \dots & a_{0,N-1}\\ a_{10}& a_{11}& \dots & a_{1,N-1}\\ \dots & \dots & & \\ a_{M-1,0}& a_{M-1,1}& \dots & a_{M-1,N-1}\end{array}\right]$$

$$\mathbf{b}=\left[\begin{array}{l}{b}_0\\ b_1\\ \dots \\ b_{M-1}\end{array}\right]$$

则方程 (2.0.1) 可以写成矩阵形式：

$$\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$$

本书中（包括此处），我们使用上标点（raised dot）表示矩阵乘法、矩阵与向量的乘法，或两个向量的点积。

这种用法是非标准的，但我们认为它能增加清晰度：在所有这些情况下，点都表示对某一对指标的求和（即缩并操作），例如：

$$\begin{array}{rl}\mathbf{C}=\mathbf{A}\cdot \mathbf{B}& ⟺c_{ik}={\sum }_j{a}_{ij}{b}_{jk}\\ \mathbf{b}=\mathbf{A}\cdot \mathbf{x}& ⟺b_i={\sum }_j{a}_{ij}{x}_j\\ \mathbf{d}=\mathbf{x}\cdot \mathbf{A}& ⟺d_j={\sum }_i{x}_i{a}_{ij}\\ q=\mathbf{x}\cdot \mathbf{y}& ⟺q={\sum }_i{x}_i{y}_i\end{array}$$

按照惯例，在矩阵中，元素 $a_{ij}$ 的第一个下标表示其所在行，第二个下标表示其所在列。在大多数情况下，你无需关心矩阵在计算机物理内存中是如何存储的；你只需通过其二维地址引用矩阵元素，例如 $a_{34}=\text{a}[3][4]$。实际上，这种 C++ 表示法可以隐藏多种微妙而灵活的物理存储方案，详见 §1.4 和 §1.5。

2.0.1 非奇异方程组与奇异方程组

你可能会疑惑，为什么在上面 $M=N$ 的情形下，我们只说有“较好”的机会求解未知数。从解析角度看，若 $M$ 个方程中有一个或多个是其余方程的线性组合（称为行退化），或者所有方程中某些变量总是以完全相同的线性组合形式出现（称为列退化），则可能不存在解（或唯一解）。对于方阵而言，行退化意味着列退化，反之亦然。这种退化的方程组称为奇异的。我们将在 §2.6 中详细讨论奇异矩阵。

从数值角度看，至少还有两个因素会阻碍我们获得良好的解：

• 尽管方程之间并非精确的线性组合，但某些方程可能非常接近线性相关，以至于机器中的舍入误差在求解过程的某个阶段使其变为线性相关。此时，你的数值方法会失败，并能告诉你它已失败。

• 求解过程中累积的舍入误差可能淹没真实解。当 $N$ 过大时，这个问题尤为突出。此时数值方法在算法上并未失败，但它返回的 $x$ 值是错误的，可通过将其直接代回原方程验证。方程组越接近奇异，这种情况越可能发生，因为在求解过程中会出现越来越接近的相消。事实上，前一种情况可视为舍入误差导致有效数字完全丢失的特例。

精心编写的“线性方程求解软件包”的大部分复杂性都用于检测和/或修正上述两种病态情况。很难给出何时需要这种复杂性的明确准则，因为不存在“典型”的线性问题。但这里有一个粗略的参考：若 $N$ 不超过 20 或 50 且方程组不接近奇异，则这类线性方程组属于常规问题；即使仅使用单精度（即 float），通常也无需比最直接的方法更复杂的技术。若使用双精度，这一规模可轻松扩展到 $N$ 约为 1000；此后，限制因素通常变为机器时间而非精度。

当系数矩阵稀疏（即大部分元素为零）时，即使 $N$ 达到数千或数百万，也可利用稀疏性求解。我们将在 §2.7 中进一步讨论。

不幸的是，人们经常会遇到本质上接近奇异的线性问题。此时，即使 $N=10$（尽管 $N=5$ 时很少见），也可能需要采用复杂的方法。奇异值分解（§2.6）是一种有时能将奇异问题转化为非奇异问题的技术，此时额外的复杂性就不再必要了。

2.0.2 计算线性代数的任务

线性代数远不止求解单个右端项的单一方程组。以下列出本章涉及的主要主题。（第 11 章将继续讨论特征值/特征向量问题。）

当 $M=N$ 时：

• 求解矩阵方程 $\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$ 中的未知向量 $\mathbf{x}$（§2.1 – §2.10）。

• 求解多个矩阵方程 $\mathbf{A}\cdot {\mathbf{x}}_j={\mathbf{b}}_j$，其中 ${\mathbf{x}}_j$（$j=0,1,\dots$）是一组向量，每个对应一个不同的已知右端项向量 ${\mathbf{b}}_j$。此任务的关键简化在于矩阵 $\mathbf{A}$ 保持不变，仅右端项 $\mathbf{b}$ 改变（§2.1 – §2.10）。

• 计算方阵 $\mathbf{A}$ 的逆矩阵 ${\mathbf{A}}^{-1}$，即满足 $\mathbf{A}\cdot {\mathbf{A}}^{-1}={\mathbf{A}}^{-1}\cdot \mathbf{A}=1$ 的矩阵，其中 $1$ 为单位矩阵（对角线元素为 1，其余为 0）。对于 $N\times N$ 矩阵 $\mathbf{A}$，此任务等价于前一任务中取 $N$ 个不同的 ${\mathbf{b}}_j$（$j=0,1,\dots ,N-1$），即单位向量（${\mathbf{b}}_j$ 除第 $j$ 个分量为 1 外，其余均为 0）。对应的 $\mathbf{x}$ 即为 ${\mathbf{A}}^{-1}$ 的各列（§2.1 和 §2.3）。

• 计算方阵 $\mathbf{A}$ 的行列式（§2.3）。

若 $M<N$，或 $M=N$ 但方程退化，则有效方程数少于未知数。此时可能无解，或存在多个解向量 $\mathbf{x}$。后一种情况下，解空间由一个特解 ${\mathbf{x}}_p$ 加上（通常）$N-M$ 个向量的任意线性组合构成（这些向量称为矩阵 $\mathbf{A}$ 的零空间中的向量）。求 $\mathbf{A}$ 的解空间的任务涉及

• 矩阵 A 的奇异值分解（§2.6）。

当方程个数多于未知数个数（即 $M>N$）时，方程 (2.0.1) 通常不存在解向量 $\mathbf{x}$，此时称该方程组为超定方程组（overdetermined）。然而，经常需要寻找一个最佳的“折中”解，即使得所有方程尽可能同时被满足。若以最小二乘意义来定义“接近程度”，即最小化方程 (2.0.1) 左右两边之差的平方和，则该超定线性问题可转化为一个（通常）可解的线性问题，称为：

• 线性最小二乘问题。

该问题可简化为如下 $N\times N$ 的方程组：

$$({\mathbf{A}}^{\mathbf{T}}\cdot \mathbf{A})\cdot \mathbf{x}=({\mathbf{A}}^T\cdot \mathbf{b})$$

其中 ${\mathbf{A}}^T$ 表示矩阵 $\mathbf{A}$ 的转置。方程 (2.0.5) 被称为线性最小二乘问题的正规方程（normal equations）。奇异值分解与线性最小二乘问题之间存在紧密联系，后者也在 §2.6 中讨论。需要注意的是，直接求解正规方程 (2.0.5) 通常并不是求解最小二乘问题的最佳方法。

本章还涉及以下其他主题：

• 解的迭代改进（§2.5）
• 各种特殊形式：对称正定（§2.9）、三对角（§2.4）、带状对角（§2.4）、Toeplitz（§2.8）、Vandermonde（§2.8）、稀疏矩阵（§2.7）
• Strassen 的“快速矩阵求逆”（§2.11）

2.0.3 线性代数软件

除了本书所能涵盖的内容之外，目前已有若干优秀的线性代数软件包，尽管它们并不总是提供 C++ 版本。LAPACK 是经典软件包 LINPACK 的后继者，由阿贡国家实验室（Argonne National Laboratories）开发，因其公开发布、文档齐全且可免费使用而值得特别提及。ScaLAPACK 是适用于并行架构的版本。商业软件包包括 IMSL 和 NAG 库中的相关模块。

这些高级软件包主要面向非常大规模的线性系统，因此不仅努力减少运算次数，还极力压缩所需存储空间。针对不同任务，通常会提供多个版本的例程，对应输入系数矩阵可能具有的各种简化形式：对称、三角、带状、正定等。如果你的大型矩阵属于这些特殊形式之一，务必利用相应例程所提供的更高效率，而不要仅使用适用于一般矩阵的形式。

此外，还存在一个重要的分界线，将直接法（即在可预测的运算次数内完成）与迭代法（即通过若干步迭代逐步逼近所需解）区分开来。当由于 $N$ 过大或问题接近奇异而导致数值精度严重损失的风险较高时，迭代法往往更为可取。本书仅部分涉及迭代法，相关内容见 §2.7 以及第 19 和 20 章。这些方法虽然重要，但大多超出了本书的范围。不过，我们将详细讨论一种介于直接法与迭代法之间的技术，即对通过直接法获得的解进行迭代改进（§2.5）。

参考文献

Golub, G.H., and Van Loan, C.F. 1996, Matrix Computations, 3rd ed. (Baltimore: Johns Hopkins University Press).

Gill, P.E., Murray, W., and Wright, M.H. 1991, Numerical Linear Algebra and Optimization, vol. 1 (Redwood City, CA: Addison-Wesley).

Stoer, J., and Bulirsch, R. 2002, Introduction to Numerical Analysis, 3rd ed. (New York: Springer), Chapter 4.

Ueberhuber, C.W. 1997, Numerical Computation: Methods, Software, and Analysis, 2 vols. (Berlin: Springer), Chapter 13.

Coleman, T.F., and Van Loan, C. 1988, Handbook for Matrix Computations (Philadelphia: S.I.A.M.).
Forsythe, G.E., and Moler, C.B. 1967, Computer Solution of Linear Algebraic Systems (Englewood Cliffs, NJ: Prentice-Hall).

Wilkinson, J.H., and Reinsch, C. 1971, Linear Algebra, vol. II of Handbook for Automatic Computation (New York: Springer).

Westlake, J.R. 1968, A Handbook of Numerical Matrix Inversion and Solution of Linear Equations (New York: Wiley).

Johnson, L.W., and Riess, R.D. 1982, Numerical Analysis, 2nd ed. (Reading, MA: Addison-Wesley), Chapter 2.

Ralston, A., and Rabinowitz, P. 1978, A First Course in Numerical Analysis, 2nd ed.; reprinted 2001 (New York: Dover), Chapter 9.

2.1 高斯-约当消元法

高斯-约当消元法（Gauss-Jordan elimination）可能是你在高中时学习求解线性方程组的方法。（你可能学过它被称为“高斯消元法”，但严格来说，该术语指的是 §2.2 中讨论的略有不同的方法。）其基本思想是通过对给定方程进行线性组合的加减运算，直到每个方程仅包含一个未知数，从而直接得到解。你可能也学过用相同的方法计算矩阵的逆。

对于求解线性方程组，高斯-约当消元法不仅能对一个或多个右端向量 $\mathbf{b}$ 求出方程组的解，还能同时得到矩阵的逆 ${\mathbf{A}}^{-1}$。然而，该方法的主要缺点是：(i) 它要求所有右端向量必须同时存储并参与运算；(ii) 当不需要求矩阵逆时，对于单个线性方程组，高斯-约当法的速度比最佳替代方法（§2.3）慢三倍。该方法的主要优点在于其数值稳定性与其他直接法相当，甚至在使用全主元（full pivoting）时可能略胜一筹（见 §2.1.2）。

对于矩阵求逆，高斯-约当消元法的效率与其他直接法大致相当。如果你确定真正需要的是矩阵的逆，那么没有理由不在此应用中使用该方法。

你可能会对上述缺点 (i) 产生疑问：既然我们已经得到了矩阵的逆，难道不能用它乘以一个新的右端向量来获得额外的解吗？这确实可行，但所得结果对舍入误差极为敏感，其精度远不如在最初就将该新向量包含在右端向量集合中进行求解。

因此，高斯-约当消元法不应作为求解线性方程组的首选方法。§2.3 中介绍的分解方法更为优越。那么，我们为何还要讨论高斯-约当法呢？因为它思路清晰、稳健可靠，并且是我们引入主元选择（pivoting）这一重要概念的良好起点，而主元选择在后续方法中同样至关重要。

对后面描述的方法非常重要。高斯-约当消元法中实际执行的操作顺序，与接下来两节中例程所执行的操作顺序密切相关。

2.1.1 列增广矩阵上的消元

为了清晰起见，并避免无休止地书写省略号（$\cdots$），我们仅写出四个方程、四个未知数的情形，并假设有三个预先已知的不同右侧向量。你可以写出更大的矩阵，并以完全类似的方式将方程推广到 $N\times N$ 矩阵、$M$ 组右侧向量的情形。当然，下面 §2.1.2 中实现的例程是通用的。

考虑线性矩阵方程

$$\begin{array}{rl}\left[\begin{array}{llll}{a}_{00}& a_{01}& a_{02}& a_{03}\\ a_{10}& a_{11}& a_{12}& a_{13}\\ a_{20}& a_{21}& a_{22}& a_{23}\\ a_{30}& a_{31}& a_{32}& a_{33}\end{array}\right]\cdot \left[\begin{array}{l}{x}_{00}\\ x_{10}\\ x_{20}\\ x_{30}\end{array}\right|\begin{array}{l}{x}_{01}\\ x_{11}\\ x_{21}\\ x_{31}\end{array}|\begin{array}{l}{x}_{02}\\ x_{12}\\ x_{22}\\ x_{32}\end{array}|\begin{array}{l}{y}_{00}\\ y_{10}\\ y_{20}\\ y_{30}\end{array}|\begin{array}{l}{y}_{01}\\ y_{11}\\ y_{21}\\ y_{31}\end{array}|\begin{array}{l}{y}_{02}\\ y_{12}\\ y_{22}\\ y_{32}\end{array}|\begin{array}{l}{b}_{00}\\ b_{10}\\ b_{20}\\ b_{30}\end{array}|\begin{array}{l}{b}_{01}\\ b_{11}\\ b_{21}\\ b_{31}\end{array}|\begin{array}{l}{b}_{02}\\ b_{12}\\ b_{22}\\ b_{32}\end{array}|\begin{array}{l}1\\ 0\\ 0\\ 0\end{array}|\begin{array}{l}0\\ 1\\ 0\\ 0\end{array}|\begin{array}{l}0\\ 0\\ 1\\ 0\end{array}|\begin{array}{l}0\\ 0\\ 0\\ 1\end{array}]& (\mathrm{2.1.1})\end{array}$$

此处的中心点（·）表示矩阵乘法，而运算符 $\bigsqcup$ 仅表示列增广，即去掉相邻的括号，将 $\bigsqcup$ 运算符的操作数合并成一个更宽的矩阵。

你很快就能写出方程 (2.1.1)，并看出它实际上说明：$x_{ij}$ 是第 $j$ 个右侧向量（$j=0,1,2$）对应解向量的第 $i$ 个分量（$i=0,1,2,3$），该右侧向量的系数为 $b_{ij}$（$i=0,1,2,3$）；而未知系数矩阵 $y_{ij}$ 则是 $a_{ij}$ 的逆矩阵。换句话说，矩阵方程

$$[\mathbf{A}]\cdot [{\mathbf{x}}_0\bigsqcup {\mathbf{x}}_1\bigsqcup {\mathbf{x}}_2\bigsqcup \mathbf{Y}]=[{\mathbf{b}}_0\bigsqcup {\mathbf{b}}_1\bigsqcup {\mathbf{b}}_2\bigsqcup 1]$$

其中 $\mathbf{A}$ 和 $\mathbf{Y}$ 为方阵，${\mathbf{b}}_i$ 和 ${\mathbf{x}}_i$ 为列向量，$1$ 为单位矩阵，同时求解了以下线性方程组：

$$\mathbf{A}\cdot {\mathbf{x}}_0={\mathbf{b}}_0\mathbf{A}\cdot {\mathbf{x}}_1={\mathbf{b}}_1\mathbf{A}\cdot {\mathbf{x}}_2={\mathbf{b}}_2$$

以及

$$\mathbf{A}\cdot \mathbf{Y}=1$$

现在，关于 (2.1.1) 还有一些基本事实很容易验证：

• 交换 $\mathbf{A}$ 的任意两行，同时交换 $\mathbf{b}$ 和 $1$ 中对应的行，不会改变（或以任何方式打乱）解 $\mathbf{x}$ 和 $\mathbf{Y}$。这仅仅相当于以不同的顺序书写同一组线性方程。

• 同样，如果我们用某一行与另一行的线性组合来替换 $\mathbf{A}$ 中的任意一行（只要对 $\mathbf{b}$ 和 $1$ 的行进行相同的线性组合），解集也不会改变或被打乱（当然，此时 $1$ 不再是单位矩阵）。

• 交换 $\mathbf{A}$ 的任意两列，只有在同时交换 $\mathbf{x}$ 和 $\mathbf{Y}$ 中对应的行时，才能得到相同的解集。换句话说，这种交换会打乱解中行的顺序。如果这样做，我们需要通过将行恢复到原始顺序来“解乱”解。

高斯-约当消元法利用上述一个或多个操作，将矩阵 $\mathbf{A}$ 化简为单位矩阵。一旦完成此操作，右侧即成为解集，这从 (2.1.2) 可以立即看出。

2.1.2 选主元（Pivoting）

在“无选主元的高斯-约当消元法”中，仅使用上述列表中的第二种操作。首先将第 0 行除以元素 $a_{00}$（这相当于第 0 行与其他行的线性组合，其他行的系数为零）。然后从其他各行中减去适当倍数的第 0 行，使得所有剩余的 $a_{i0}$（$i>0$）变为零。此时 $\mathbf{A}$ 的第 0 列已与单位矩阵一致。接着处理第 1 列：将第 1 行除以 $a_{11}$，然后从第 0、2、3 行中减去适当倍数的第 1 行，使它们在第 1 列的元素变为零。第 1 列现在也化为单位形式。依此类推，处理第 2 列和第 3 列。在对 $\mathbf{A}$ 执行这些操作的同时，当然也要对 $\mathbf{b}$ 和 $1$ 执行相应的操作（此时 $1$ 已完全不像单位矩阵了！）。

显然，如果在需要除以对角线元素时，遇到（当前）对角线上的零元素，就会出现问题。（顺便提一下，我们用来除的元素称为主元或枢纽元（pivot）。）不太明显但确实成立的是：即使没有遇到零主元，在存在舍入误差的情况下，不选主元的高斯-约当消元法（即不使用上述列表中的第一或第三种操作）在数值上是不稳定的。你绝不能在不选主元的情况下执行高斯-约当消元法（或高斯消元法；见下文）！

那么，这种神奇的选主元究竟是什么呢？不过是交换行（部分选主元）或交换行和列（完全选主元），以便将一个特别理想的元素放到即将选择主元的对角位置上。由于我们不想打乱已经构建好的单位矩阵部分，因此只能在满足以下两个条件的元素中选择：(i) 位于即将被归一化的行及其下方的行中；(ii) 位于即将被消去的列及其右侧的列中。部分选主元比完全选主元更简单，因为我们不需要跟踪解向量的置换。部分选主元只能在当前列中已有的元素中选择主元。事实证明，部分选主元“几乎”和完全选主元一样好，这一点可以严格数学化（但此处无需深究；参见 [1] 的讨论和参考文献）。为了向你展示两种变体，本节的例程使用完全选主元，而 §2.3 使用部分选主元。

接下来需要说明如何识别一个特别理想的主元。理论上对此尚无完全明确的答案。但理论和实践都表明，简单地选择（绝对值）最大的可用元素作为主元是一个非常好的选择。然而，这种方法的一个奇特之处在于，主元的选择依赖于方程原始的缩放比例。例如，如果我们把原始方程组中的第三个方程乘以一百万，几乎可以肯定它会提供第一个主元；但方程的底层解并不会因这一乘法而改变！因此，有时会看到一些例程选择主元的方式是：假设原始方程都被缩放，使得其最大系数归一化为 1，然后在此假设下选择最大的元素作为主元。这称为隐式选主元（implicit pivoting）。为此需要额外记录各行本应乘以的缩放因子。（§2.3 中的例程包含隐式选主元，但本节的例程不包含。）

最后，我们考虑该方法的存储需求。稍加思考即可发现，在算法的每个阶段，$\mathbf{A}$ 中的某个元素要么可预测地为 1 或 0（如果它已处于被化简为单位矩阵的部分），要么其在初始为 $1$ 的矩阵中完全对应位置的元素可预测地为 1 或 0（如果 $\mathbf{A}$ 中对应的元素尚未被化简为单位形式）。因此，$1$ 无需作为独立存储存在：$\mathbf{A}$ 的逆矩阵在原始 $\mathbf{A}$ 被逐步销毁的同时，逐渐在 $\mathbf{A}$ 的存储空间中构建起来。同样，解向量 $\mathbf{x}$ 可以逐步替换右侧向量 $\mathbf{b}$，并共享相同的存储空间，因为在 $\mathbf{A}$ 中每消去一列后，$\mathbf{b}$ 中对应的行元素就不再被使用。

以下是一个执行完全选主元高斯-约当消元的例程，它将输入矩阵替换为所需的答案。紧随其后的是一个重载版本，用于没有右侧向量的情形，即仅需求矩阵逆的情形。

void gaussj(MatDoub_IO &a, MatDoub_IO &b)

通过高斯-约当消元法求解线性方程组，对应上述方程 (2.1.1)。输入矩阵为 a[0..n-1][0..n-1]。b[0..n-1][0..m-1] 输入包含 $m$ 个右侧向量。输出时，a 被替换为其矩阵逆，b 被替换为对应的解向量集。

Int i, icol, irow, j, k, l, ll, n = a.nrows(), m = b.ncols();
Doub big, dum, pivinv;
VecInt indxc(n), indxr(n), ipiv(n);

for (j=0;j<n;j++) ipiv[j]=0;

for (i=0;i<n;i++) {
    big=0.0;
    for (j=0;j<n;j++) {
        if (ipiv[j] != 1)
            for (k=0;k<n;k++) {
            if (ipiv[k] == 0) {
                if (abs(a[j][k]) >= big) {
                big=abs(a[j][k]);
                irow=j;
                icol=k;
                }
            }
        }
    }
}
++(ipiv[icol]);

我们现在得到了主元元素，因此如有必要，交换行以将主元元素放到对角线上。列并不实际交换，仅重新标记：indexc[i] 是第 (i+1) 个主元元素所在的列，即第 (i+1) 个被消元的列；而 indexr[i] 是该主元元素最初所在的行。如果 indexr[i] ≠ indexc[i]，则意味着发生了列交换。通过这种记录方式，解向量 b 最终会处于正确的顺序，而逆矩阵的列则会被打乱。

现在我们准备用主元元素（位于 irow 和 icol）去除主元行。

indexc[i]=icol;
if (a[icol][icol] == 0.0) throw("gaussj: 奇异矩阵");
pivinv=1.0/a[icol][icol];
a[icol][icol]=1.0;
for (l=0;l<n;l++) a[icol][l] *= pivinv;
for (l=0;l<m;l++) b[icol][l] *= pivinv;
for (ll=0;ll<n;ll++) // 接下来，我们消去其他行...
if (ll != icol) {
    dum=a[ll][icol];
    a[ll][icol]=0.0;
    for (l=0;l<n;l++) a[ll][l] -= a[icol][l]*dum;
    for (l=0;l<m;l++) b[ll][l] -= b[icol][l]*dum;
    }
}

这是按列进行消元的主循环的结束。现在只需根据列交换的情况对解向量进行还原。我们通过按构造置换的逆序交换列对来实现这一点。

for (l=n-1;l>=0;l--) {
    if (indexr[l] != indexc[l])
        for (k=0;k<n;k++) SWAP(a[k][indexr[l]],a[k][indexc[l]]);
    }
}

void gaussj(MatDoub_IO &a) // 无右端项的重载版本，将 a 替换为其逆矩阵。 { MatDoub b(a.nrows(),0); gaussj(a,b); }

2.1.3 行消元与列消元策略

上述讨论可以通过少量形式化方法加以扩展。对矩阵 $\mathbf{A}$ 的行操作对应于左乘（即前置）某个简单矩阵 $\mathbf{R}$。例如，具有如下分量的矩阵 $\mathbf{R}$：

$$R_{ij}=\{\begin{array}{ll}1& \mathrm{若}i=j\mathrm{且}i\ne 2,4\\ 1& \mathrm{若}i=2,j=4\\ 1& \mathrm{若}i=4,j=2\\ 0& \mathrm{其他情况}\end{array}$$

实现了第 2 行与第 4 行的交换。仅使用行操作（包括部分主元选取的可能性）的高斯-约当消元法由一系列这样的左乘操作组成，依次得到：

$$\begin{array}{rl}& \mathbf{A}\cdot \mathbf{x}=\mathbf{b}\\ & (\cdots {\mathbf{R}}_2\cdot {\mathbf{R}}_1\cdot {\mathbf{R}}_0\cdot \mathbf{A})\cdot \mathbf{x}=\cdots {\mathbf{R}}_2\cdot {\mathbf{R}}_1\cdot {\mathbf{R}}_0\cdot \mathbf{b}\\ & (1)\cdot \mathbf{x}=\cdots {\mathbf{R}}_2\cdot {\mathbf{R}}_1\cdot {\mathbf{R}}_0\cdot \mathbf{b}\end{array}$$

关键点在于，由于 $\mathbf{R}$ 矩阵是从右向左累积的，因此右端项在每个阶段仅是从一个向量变换为另一个向量。

另一方面，列操作对应于右乘（即后置）简单矩阵，记为 $\mathbf{C}$。若将方程 (2.1.5) 中的矩阵右乘到矩阵 $\mathbf{A}$ 上，将交换 $\mathbf{A}$ 的第 2 列和第 4 列。列操作消元法（概念上）需要在矩阵 $\mathbf{A}$ 与未知向量 $\mathbf{x}$ 之间插入一个列操作矩阵及其逆矩阵：

$$\begin{array}{rlr}& & \mathbf{A}\cdot \mathbf{x}=\mathbf{b}\\ & & \mathbf{A}\cdot {\mathbf{C}}_0\cdot {\mathbf{C}}_0^{-1}\cdot \mathbf{x}=\mathbf{b}\\ & & \mathbf{A}\cdot {\mathbf{C}}_0\cdot {\mathbf{C}}_1\cdot {\mathbf{C}}_1^{-1}\cdot {\mathbf{C}}_0^{-1}\cdot \mathbf{x}=\mathbf{b}\\ & & (\mathbf{A}\cdot {\mathbf{C}}_0\cdot {\mathbf{C}}_1\cdot {\mathbf{C}}_2\cdots )\cdots {\mathbf{C}}_2^{-1}\cdot {\mathbf{C}}_1^{-1}\cdot {\mathbf{C}}_0^{-1}\cdot \mathbf{x}=\mathbf{b}\\ & & (1)\cdots {\mathbf{C}}_2^{-1}\cdot {\mathbf{C}}_1^{-1}\cdot {\mathbf{C}}_0^{-1}\cdot \mathbf{x}=\mathbf{b}\end{array}$$

这（逐个剥离 ${\mathbf{C}}^{-1}$）意味着解为：

$$\mathbf{x}={\mathbf{C}}_0\cdot {\mathbf{C}}_1\cdot {\mathbf{C}}_2\cdots \mathbf{b}$$

注意方程 (2.1.8) 与方程 (2.1.6) 的本质区别。在后一种情况下，$\mathbf{C}$ 必须以与它们被获知时相反的顺序作用于 $\mathbf{b}$。也就是说，它们必须在过程中全部被存储下来。这一要求大大降低了列操作的实用性，通常将其限制为简单的置换操作，例如用于完全主元选取。

参考文献

Wilkinson, J.H. 1965, The Algebraic Eigenvalue Problem (New York: Oxford University Press).[1] Carnahan, B., Luther, H.A., and Wilkes, J.O. 1969, Applied Numerical Methods (New York: Wiley), Example 5.2, p. 282.

Bevington, P.R., and Robinson, D.K. 2002, Data Reduction and Error Analysis for the Physical Sciences, 3rd ed. (New York: McGraw-Hill), p. 247.

Westlake, J.R. 1968, A Handbook of Numerical Matrix Inversion and Solution of Linear Equations (New York: Wiley).

Ralston, A., and Rabinowitz, P. 1978, A First Course in Numerical Analysis, 2nd ed.; reprinted 2001 (New York: Dover), §9.3–1.

2.2 带回代的高斯消元法

任何关于带回代的高斯消元法的讨论主要是教学性质的。该方法介于高斯-约当等完全消元方案与下一节将讨论的三角分解方案之间。高斯消元法并不将矩阵完全化为单位矩阵，而只进行到一半，得到一个对角线及其上方（例如）元素仍非平凡的矩阵。现在我们来看看这种方法有何优势。

假设在执行 §2.1 中描述的高斯-约当消元时，我们在每个阶段仅用当前主元元素下方的行进行消元。例如，当 $a_{11}$ 为主元元素时，我们将第 1 行除以其值（如前所述），但现在仅用主元行将 $a_{21}$ 和 $a_{31}$ 归零，而不处理 $a_{01}$（参见方程 2.1.1）。同时，我们仅使用部分主元选取，从不交换列，因此未知数的顺序无需修改。

那么，当我们对所有主元都完成此操作后，将得到如下形式的简化方程（以单个右端向量为例）：

$$\begin{array}{r}\left[\begin{array}{llll}{a}_{00}^{\prime }& a_{01}^{\prime }& a_{02}^{\prime }& a_{03}^{\prime }\\ 0& a_{11}^{\prime }& a_{12}^{\prime }& a_{13}^{\prime }\\ 0& 0& a_{22}^{\prime }& a_{23}^{\prime }\\ 0& 0& 0& a_{33}^{\prime }\end{array}\right]\cdot \left[\begin{array}{l}{x}_0\\ x_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{l}{b}_0^{\prime }\\ b_1^{\prime }\\ b_2^{\prime }\\ b_3^{\prime }\end{array}\right]\end{array}$$

此处的撇号表示 $a$ 和 $b$ 不再具有其原始数值，而是已被到目前为止消元过程中所有的行变换所修改。到此为止的步骤称为高斯消元法。

2.2.1 回代

但我们如何求解未知数 $x$ 呢？最后一个未知数（在此例中为 $x_3$）已经被分离出来，即

$$x_3=b_3^{\prime }/a_{33}^{\prime }$$

一旦已知最后一个 $x$，我们就可以求解倒数第二个 $x$：

$$x_2=\frac{1}{a_{22}^{\prime }}[b_2^{\prime }-x_3{a}_{23}^{\prime }]$$

然后继续向前求解前一个 $x$。一般步骤为：

$$x_i=\frac{1}{a_{ii}^{\prime }}[b_i^{\prime }-\sum _{j=i+1}^N{a}_{ij}^{\prime }{x}_j]$$

由式 (2.2.4) 所定义的步骤称为回代（backsubstitution）。高斯消元法与回代相结合，即可求得方程组的解。

高斯消元法加回代相较于高斯-若尔当消元法的优势仅在于其原始运算量更少：高斯-若尔当消元法最内层循环（每次包含一次减法和一次乘法）的执行次数为 $N^3$ 次和 $N^{2}m$ 次（其中 $N$ 为方程与未知数的个数，$m$ 为不同右侧向量的个数）。而高斯消元法对应的循环仅执行 $\frac{1}{3}{N}^3$ 次（仅需化简一半矩阵，且随着可预测零元素的增多，运算量进一步降至三分之一）和 $\frac{1}{2}{N}^{2}m$ 次。每次对一个右侧向量进行回代需要执行 $\frac{1}{2}{N}^2$ 次类似的循环（一次乘法加一次减法）。当 $m\ll N$（即右侧向量很少）时，高斯消元法的速度大约是高斯-若尔当消元法的三倍。（若在高斯-若尔当方法中不计算逆矩阵，则此优势可降至 1.5 倍。）

对于计算逆矩阵的情形（可视为 $m=N$ 个右侧向量的情形，即单位矩阵的 $N$ 个列向量），乍看之下，高斯消元法加回代需要 $\frac{1}{3}{N}^3$（矩阵约简）$+\frac{1}{2}{N}^3$（右侧向量处理）$+\frac{1}{2}{N}^3$（$N$ 次回代）$=\frac{4}{3}{N}^3$ 次循环操作，多于高斯-若尔当法的 $N^3$ 次。然而，单位向量非常特殊，其中除一个元素外其余全为零。若考虑这一特性，右侧向量的处理可减少至仅 $\frac{1}{6}{N}^3$ 次循环操作。因此，在矩阵求逆问题上，两种方法的效率实际上是相同的。

高斯消元法和高斯-若尔当消元法都有一个共同缺点：所有右侧向量必须事先已知。下一节介绍的 $LU$ 分解法则没有这一缺陷，并且在求解任意数量右侧向量或矩阵求逆时，其运算量同样很小。

参考文献

Ralston, A., and Rabinowitz, P. 1978, A First Course in Numerical Analysis, 2nd ed.; reprinted 2001 (New York: Dover), §9.3–1.

Isaacson, E., and Keller, H.B. 1966, Analysis of Numerical Methods; reprinted 1994 (New York: Dover), §2.1.

Johnson, L.W., and Riess, R.D. 1982, Numerical Analysis, 2nd ed. (Reading, MA: Addison-Wesley), §2.2.1.

Westlake, J.R. 1968, A Handbook of Numerical Matrix Inversion and Solution of Linear Equations (New York: Wiley).

2.3 LU 分解及其应用

假设我们可以将矩阵 $\mathbf{A}$ 写成两个矩阵的乘积：

$$\mathbf{L}\cdot \mathbf{U}=\mathbf{A}$$

其中 $\mathbf{L}$ 是下三角矩阵（仅在对角线及其下方有非零元素），$\mathbf{U}$ 是上三角矩阵（仅在对角线及其上方有非零元素）。例如，对于一个 $4\times 4$ 的矩阵 $\mathbf{A}$，式 (2.3.1) 可表示为：

$$\left[\begin{array}{llll}{\alpha }_{00}& 0& 0& 0\\ {\alpha }_{10}& {\alpha }_{11}& 0& 0\\ {\alpha }_{20}& {\alpha }_{21}& {\alpha }_{22}& 0\\ {\alpha }_{30}& {\alpha }_{31}& {\alpha }_{32}& {\alpha }_{33}\end{array}\right]\cdot \left[\begin{array}{llll}{\beta }_{00}& {\beta }_{01}& {\beta }_{02}& {\beta }_{03}\\ 0& {\beta }_{11}& {\beta }_{12}& {\beta }_{13}\\ 0& 0& {\beta }_{22}& {\beta }_{23}\\ 0& 0& 0& {\beta }_{33}\end{array}\right]=\left[\begin{array}{llll}{a}_{00}& a_{01}& a_{02}& a_{03}\\ a_{10}& a_{11}& a_{12}& a_{13}\\ a_{20}& a_{21}& a_{22}& a_{23}\\ a_{30}& a_{31}& a_{32}& a_{33}\end{array}\right]$$

我们可以利用如 (2.3.1) 所示的分解来求解线性方程组：

$$\mathbf{A}\cdot \mathbf{x}=(\mathbf{L}\cdot \mathbf{U})\cdot \mathbf{x}=\mathbf{L}\cdot (\mathbf{U}\cdot \mathbf{x})=\mathbf{b}$$

首先求解向量 $\mathbf{y}$，使得

$$\mathbf{L}\cdot \mathbf{y}=\mathbf{b}$$

然后再求解

$$\mathbf{U}\cdot \mathbf{x}=\mathbf{y}$$

将一个线性方程组拆分为两个连续的三角方程组有什么优势呢？其优势在于，求解三角形方程组非常简单，因为

我们已经在 §2.2 中见过（见公式 2.2.4）。因此，公式 (2.3.4) 可通过前向代入法求解，如下所示：

$$\begin{array}{rl}& y_0=\frac{b_0}{{\alpha }_{00}}\\ & y_i=\frac{1}{{\alpha }_{ii}}[b_i-{\sum }_{j=0}^{i-1}{\alpha }_{ij}{y}_j]i=1,2,\dots ,N-1\end{array}$$

而 (2.3.5) 则可通过回代法求解，其形式与公式 (2.2.2)–(2.2.4) 完全相同：

$$\begin{array}{rl}& x_{N-1}=\frac{y_{N-1}}{{\beta }_{N-1,N-1}}\\ & x_i=\frac{1}{{\beta }_{ii}}[y_i-{\sum }_{j=i+1}^{N-1}{\beta }_{ij}{x}_j]i=N-2,N-3,\dots ,0\end{array}$$

公式 (2.3.6) 和 (2.3.7) 对每个右端向量 $\mathbf{b}$ 总共需要执行 $N^2$ 次内层循环，每次循环包含一次乘法和一次加法。如果我们有 $N$ 个右端向量，且它们是单位列向量（即我们在对矩阵求逆的情形），那么考虑到前导零的存在，(2.3.6) 的总执行次数将从 $\frac{1}{\gamma }{N}^3$ 减少到 $\frac{1}{\kappa }{N}^3$，而 (2.3.7) 的执行次数仍保持为 $\frac{1}{\gamma }{N}^3$。

注意，一旦我们得到了矩阵 $\mathbf{A}$ 的 $LU$ 分解，就可以依次求解任意多个右端向量。这相对于 §2.1 和 §2.2 中的方法是一个明显的优势。

2.3.1 执行 LU 分解

那么，给定 $\mathbf{A}$，我们如何求解 $\mathbf{L}$ 和 $\mathbf{U}$ 呢？首先，我们写出公式 (2.3.1) 或 (2.3.2) 的第 $i,j$ 个分量。该分量总是一个以如下形式开始的求和式：

$${\alpha }_{i0}{\beta }_{0j}+\cdots =a_{ij}$$

然而，求和项的数量取决于 $i$ 和 $j$ 中哪个更小。实际上，我们有以下三种情形：

$$\begin{array}{rl}i<j:& {\alpha }_{i0}{\beta }_{0j}+{\alpha }_{i1}{\beta }_{1j}+\cdots +{\alpha }_{ii}{\beta }_{ij}=a_{ij}\\ i=j:& {\alpha }_{i0}{\beta }_{0j}+{\alpha }_{i1}{\beta }_{1j}+\cdots +{\alpha }_{ii}{\beta }_{jj}=a_{ij}\\ i>j:& {\alpha }_{i0}{\beta }_{0j}+{\alpha }_{i1}{\beta }_{1j}+\cdots +{\alpha }_{ij}{\beta }_{jj}=a_{ij}\end{array}$$

公式 (2.3.8)–(2.3.10) 总共提供了 $N^2$ 个方程，用于求解 $N^2+N$ 个未知数 $\alpha$ 和 $\beta$（对角线元素被重复计算了一次）。由于未知数多于方程数，我们可以任意指定其中 $N$ 个未知数，然后尝试求解其余未知数。事实上，正如我们将看到的，总是可以取

$${\alpha }_{ii}\equiv 1i=0,\dots ,N-1$$

现在介绍一种令人惊讶的方法——克劳特算法（Crout's algorithm），它通过将方程按特定顺序排列，就能非常简单地求解全部 $N^2+N$ 个方程 $(\mathrm{2.3.8})-(\mathrm{2.3.11})$，从而得到所有的 $\alpha$ 和 $\beta$。该顺序如下：

• 设 ${\alpha }_{ii}=1,i=0,\dots ,N-1$（公式 2.3.11）。

• 对每个 $j=0,1,2,\dots ,N-1$，执行以下两个步骤：
  首先，对 $i=0,1,\dots ,j$，利用 (2.3.8)、(2.3.9) 和 (2.3.11) 求解 ${\beta }_{ij}$，即

$${\beta }_{ij}=a_{ij}-\sum _{k=0}^{i-1}{\alpha }_{ik}{\beta }_{kj}$$

（当 $i=0$ 时，公式 2.3.12 中的求和项视为零。）
其次，对 $i=j+1,j+2,\dots ,N-1$，利用 (2.3.10) 求解 ${\alpha }_{ij}$，即

$${\alpha }_{ij}=\frac{1}{{\beta }_{jj}}\left(a_{ij}-\sum _{k=0}^{j-1}{\alpha }_{ik}{\beta }_{kj}\right)$$

务必在进入下一个 $j$ 之前完成这两个步骤。

如果你手动执行上述过程的几次迭代，就会发现公式 (2.3.12) 和 (2.3.13) 右侧出现的 $\alpha$ 和 $\beta$ 在需要时已经被计算出来了。你还会发现每个 $a_{ij}$ 仅被使用一次，之后就不再需要。这意味着对应的 ${\alpha }_{ij}$ 或 ${\beta }_{ij}$ 可以直接存储在原来 $a_{ij}$ 所在的位置：分解是“原地”进行的。[对角线上的单位元素 ${\alpha }_{ii}$（公式 2.3.11）根本不需要存储。] 简而言之，克劳特方法按列从左到右、每列内从上到下（见图 2.3.1）填充如下所示的 $\alpha$ 和 $\beta$ 的组合矩阵：

$$\left[\begin{array}{llll}{\beta }_{00}& {\beta }_{01}& {\beta }_{02}& {\beta }_{03}\\ {\alpha }_{10}& {\beta }_{11}& {\beta }_{12}& {\beta }_{13}\\ {\alpha }_{20}& {\alpha }_{21}& {\beta }_{22}& {\beta }_{23}\\ {\alpha }_{30}& {\alpha }_{31}& {\alpha }_{32}& {\beta }_{33}\end{array}\right]$$

那么选主元（pivoting）呢？选主元（即为公式 2.3.13 中的除法选择一个合适的主元）对于克劳特方法的数值稳定性至关重要。只有部分选主元（即行交换）能够高效地实现，但这已足以保证方法的稳定性。顺便提一下，这意味着我们实际上并不是将矩阵 $\mathbf{A}$ 分解为 $LU$ 形式，而是将 $\mathbf{A}$ 的某一行置换后的矩阵进行分解。（只要我们记录下该置换，这种分解与原始分解同样有用。）

在克劳特算法中，选主元的操作稍显微妙。关键在于注意到：当 $i=j$ 时（即公式 2.3.12 的最后一次应用），它与公式 2.3.13 完全相同，唯一的区别是后者包含一次除法；在这两种情形下，求和的上限都是 $k=j-1$（即 $i-1$）。这意味着我们无需预先决定对角线元素 ${\beta }_{jj}$ 是否就是最初落在对角线上的那个元素，还是该列中其下方某个（未除的）${\alpha }_{ij}$（$i=j+1,\dots ,N-1$）将被“提升”为对角线上的 $\beta$。这个决定可以在该列所有候选元素都计算出来之后再做。正如你现在可能已经猜到的那样，我们会选择其中绝对值最大的那个作为对角线上的 $\beta$（即主元），

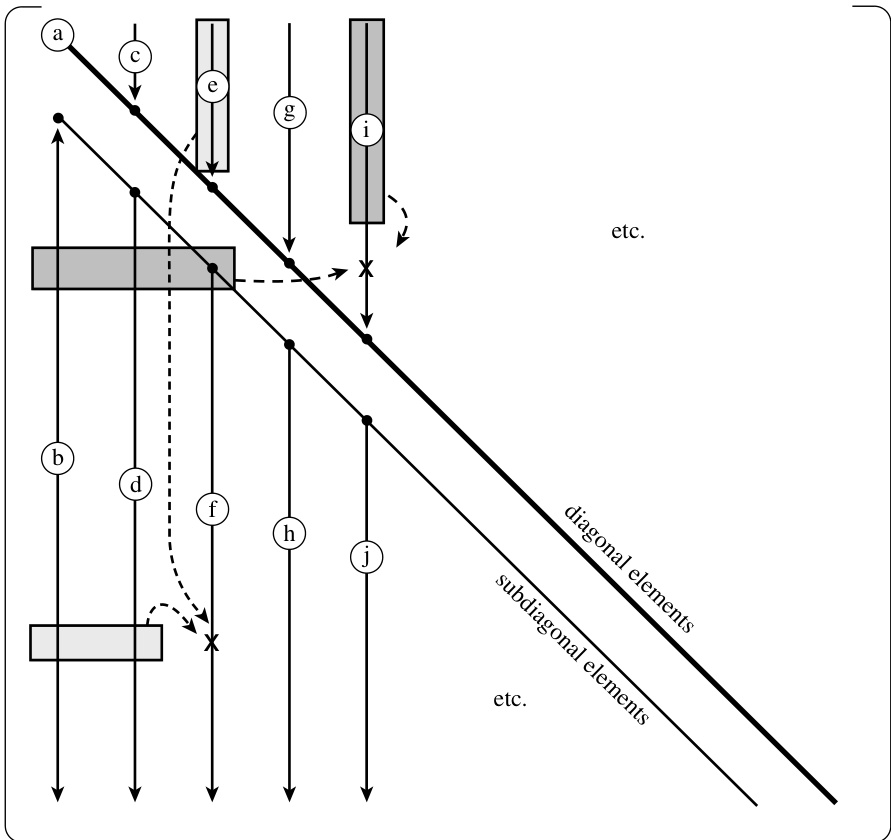
图 2.3.1. 矩阵 $LU$ 分解的克劳特算法。原始矩阵的元素按小写字母 a, b, c 等所示顺序被修改。阴影框显示了在修改两个典型元素（各用一个“X”标出）时所用到的先前已修改的元素。

然后一次性用该主元进行所有除法运算。这就是带部分选主元的克劳特方法。我们的实现还有一个额外的细节：它首先找出每行中的最大元素，随后（在寻找最大主元时）对比较进行缩放，就好像我们最初已将所有方程缩放，使得其最大系数等于 1；这就是 §2.1 中提到的隐式选主元。

$LU$ 分解的内层循环，即公式 (2.3.12) 和 (2.3.13)，类似于矩阵乘法的内层循环。它包含对指标 $i$、$j$ 和 $k$ 的三重循环。这三重循环共有六种排列顺序。克劳特算法的直接实现对应于 $jik$ 顺序，即从最外层到最内层的循环顺序依次为 $j$、$i$、$k$。在具有多级缓存的现代处理器上，且当矩阵按行存储时，通常 $kij$ 或 $ikj$ 的顺序执行速度最快。由于 $kij$ 顺序更便于实现选主元，因此我们采用这种实现方式。Golub 和 Van Loan [1] 将其称为“外积高斯消去法”。

$LU$ 分解非常适合以对象（类或结构体）的形式实现。构造函数执行分解，对象本身存储分解结果。随后，可以调用一个前向和回代方法一次或多次，以求解一个或多个右端向量。其他附加功能的方法也易于加入。该对象的声明如下所示：

udcmp.h struct LUcmp

使用 $LU$ 分解求解线性方程组 $\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$ 的对象及相关函数。

{
    Int n;
    MatDoub lu;
    VecInt idx;
    Doub d;
    LUdcmp(MatDoub_I &a);
    void solve(VecDoub_I &b, VecDoub_O &x);
    void solve(VecDoub_I &b, MatDoub_O &x);
    void inverse(MatDoub_O &ainv);
    Doub det();
    void mprove(VecDoub_I &b, VecDoub_IO &x);
    MatDoub_I &aref;
};

以下是构造函数的实现，其参数为待进行 $LU$ 分解的输入矩阵。输入矩阵不会被修改；程序会创建一个副本，并在该副本上执行外积形式的高斯消元（原地操作）。

LUdcmp::LUdcmp(MatDoub_I &a) : n(a.nrows()), lu(a), aref(a), idx(n) {
    // 给定一个矩阵 a[0..n-1][0..n-1]，此例程将其替换为自身某行置换后的 LU 分解。
    // a 为输入矩阵。输出时，其结构如上文公式 (2.3.14) 所示；
    // idx[0..n-1] 为输出向量，记录了部分主元选取过程中所执行的行置换；
    // d 输出为 ±1，分别对应行交换次数为偶数或奇数。
    // 此例程与 solve 联合使用，用于求解线性方程组或矩阵求逆。

    const Doub TINY = 1.0e-40;
    Int i, imax, j, k;
    Doub big, temp;
    VecDoub vv(n);
    d = 1.0;
    for (i = 0; i < n; i++) {
        big = 0.0;
        for (j = 0; j < n; j++)
            if ((temp = abs(lu[i][j])) > big) big = temp;
        if (big == 0.0) throw("Singular matrix in LUDCMP");
        // 没有非零的最大元素。
        vv[i] = 1.0 / big;
    }
    for (k = 0; k < n; k++) {
        big = 0.0;
        for (i = k; i < n; i++) {
            temp = vv[i] * abs(lu[i][k]);
            if (temp > big) {
                big = temp;
                imax = i;
            }
        }
        if (k != imax) {
            for (j = 0; j < n; j++) {
                temp = lu[imax][j];
                lu[imax][j] = lu[k][j];
                lu[k][j] = temp;
            }
            d = -d;
            vv[imax] = vv[k];
        }
        idx[k] = imax;
        if (lu[k][k] == 0.0) lu[k][k] = TINY;
        // 如果主元为零，则矩阵是奇异的（至少在算法精度范围内如此）。
        // 对某些奇异矩阵的应用，用 TINY 替代零是可取的。
        for (i = k + 1; i < n; i++) {
            temp = lu[i][k] / lu[k][k];  // 除以主元。
            for (j = k + 1; j < n; j++)  // 最内层循环：消去剩余子矩阵。
                lu[i][j] -= temp * lu[k][j];
        }
    }
}

一旦构造了 LUdcmp 对象，便可使用两个函数分别实现公式 (2.3.6) 和 (2.3.7) 来求解线性方程组。第一个函数求解单个右侧向量 $\mathbf{b}$ 对应的解向量 $\mathbf{x}$。第二个函数可同时求解多个右侧向量（以矩阵 $\mathbf{B}$ 的列形式给出），即计算矩阵 ${\mathbf{A}}^{-1}\cdot \mathbf{B}$。

void LUdcmp::solve(VecDoub_I &b, VecDoub_O &x)

使用已存储的 $\mathbf{A}$ 的 $LU$ 分解求解 $n$ 个线性方程 $\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$。输入向量 $\mathbf{b}[\mathrm{0..}n-1]$ 为右侧向量，解向量 $\mathbf{x}$ 通过 x 返回；b 和 x 可引用同一向量，此时解将覆盖输入。该例程考虑了 $\mathbf{b}$ 开头可能包含多个零元素的情况，因此在矩阵求逆时效率较高。

{
    Int i, ii = 0, ip, j;
    Doub sum;
    if (b.size() != n || x.size() != n)
        throw("LUdcmp::solve bad sizes");
    for (i = 0; i < n; i++) x[i] = b[i];
    for (i = 0; i < n; i++) {
        ip = idx[i];
        sum = x[ip];
        x[ip] = x[i];
        if (ii != 0)
            for (j = ii - 1; j < i; j++) sum -= lu[i][j] * x[j];
        else if (sum != 0.0)
            ii = i + 1;
        x[i] = sum;
    }
    for (i = n - 1; i >= 0; i--) {
        sum = x[i];
        for (j = i + 1; j < n; j++) sum -= lu[i][j] * x[j];
        x[i] = sum / lu[i][i];  // 存储解向量 X 的一个分量。
    }
}

void LUdcmp::solve(MatDoub_I &b, MatDoub_O &x)

使用已存储的 $\mathbf{A}$ 的 $LU$ 分解求解 $\mathbf{m}$ 组 $n$ 元线性方程 $\mathbf{A}\cdot \mathbf{X}=\mathbf{B}$。矩阵 $\mathbf{b}[\mathrm{0..}n-1][\mathrm{0..}m-1]$ 输入右侧项，$\mathbf{x}[\mathrm{0..}n-1][\mathrm{0..}m-1]$ 返回解 ${\mathbf{A}}^{-1}\cdot \mathbf{B}$。$\mathbf{b}$ 和 $\mathbf{x}$ 可引用同一矩阵，此时解将覆盖输入。

{
    Int i, j, m = b.ncols();
    if (b.nrows() != n || x.nrows() != n || b.ncols() != x.ncols())
        throw("LUdcmp::solve bad sizes");
    VecDoub xx(n);
    for (j = 0; j < m; j++) {
        for (i = 0; i < n; i++) xx[i] = b[i][j];
        solve(xx, xx);
        for (i = 0; i < n; i++) x[i][j] = xx[i];
    }
}

LUdcmp 中的 $LU$ 分解大约需要 $\frac{1}{3}{N}^3$ 次内层循环（每次包含一次乘法和一次加法）。因此，这是求解一个（或少数几个）右侧项的操作量，比 §2.1 中给出的高斯-约当消元法 gaussj 快 3 倍，也比不计算逆矩阵的高斯-约当法（未给出）快 1.5 倍。对于矩阵求逆，总操作量（包括上文公式 2.3.7 后讨论的前代和回代）为 $(\frac{1}{3}+\frac{1}{6}+\frac{1}{6})N^3=N^3$，与 gaussj 相同。

总结：求解线性方程组 $A\cdot x=b$ 的推荐方法如下：

const Int n = ...;
MatDoub a(n, n);
VecDoub b(n), x(n);
...
LUdcmp alu(a);
alu.solve(b, x);

结果将返回在 x 中。原始矩阵 a 和向量 b 不会被修改。若需释放 alu 对象占用的存储空间，可在声明 alu 前用 “{” 开始一个临时作用域，并在需要销毁 alu 时用 “}” 结束该作用域。

若后续需用相同的 $A$ 但不同的右侧向量 $b$ 求解方程组，只需重复调用：

alu.solve(b, x);

2.3.2 矩阵的逆

LUdcmp 提供了一个成员函数用于计算矩阵 $A$ 的逆。该函数简单地构造一个单位矩阵，然后调用相应的 solve 方法。

void LUdcmp::inverse(MatDoub_O &ainv)

利用已存储的 $LU$ 分解，在 ainv 中返回矩阵逆 ${\mathbf{A}}^{-1}$。

{
    Int i, j;
    ainv.resize(n, n);
    for (i = 0; i < n; i++) {
        for (j = 0; j < n; j++) ainv[i][j] = 0.0;
        ainv[i][i] = 1.0;
    }
    solve(ainv, ainv);
}

此时矩阵 ainv 将包含原始矩阵 a 的逆。或者，也可以直接使用类似 gaussj（§2.1）的高斯-约当法对矩阵原地求逆（会破坏原始矩阵）。两种方法的实际操作量基本相同。

2.3.3 矩阵的行列式

一个经过 $LU$ 分解的矩阵的行列式就是其对角线元素的乘积：

$$\det =\prod _{j=0}^{N-1}{\beta }_{jj}$$

需要提醒的是，我们并不是对原始矩阵进行分解，而是对其行置换后的矩阵进行分解。幸运的是，我们已经记录了行交换次数是偶数还是奇数，因此只需在乘积前加上相应的符号即可。（你现在终于明白 LUdcmp 结构中 d 的用途了。）

ludcmp.h

Doub LUdcmp::det()

利用已存储的 $LU$ 分解，返回矩阵 $\mathbf{A}$ 的行列式。

{
    Doub dd = d;
    for (Int i = 0; i < n; i++) dd *= lu[i][i];
    return dd;
}

对于任何规模较大的矩阵，其行列式很可能超出计算机浮点数的动态范围，导致上溢或下溢。在这种情况下，你可以轻松地添加另一个成员函数，例如通过除以 10 的幂次来单独跟踪数量级，或者分别累加各因子绝对值的对数之和与符号。

2.3.4 复数方程组

如果你的矩阵 $\mathbf{A}$ 是实矩阵，但右端向量是复数，例如 $\mathbf{b}+i\mathbf{d}$，那么可以按以下步骤求解：(i) 用常规方法对 $\mathbf{A}$ 进行 $LU$ 分解；(ii) 对 $\mathbf{b}$ 进行回代，得到解向量的实部；(iii) 对 $\mathbf{d}$ 进行回代，得到解向量的虚部。

如果矩阵本身是复数，即需要求解如下方程组：

$$\begin{array}{r}(\mathbf{A}+i\mathbf{C})\cdot (\mathbf{x}+i\mathbf{v})=(\mathbf{b}+i\mathbf{d})\end{array}$$

此时有两种处理方法。最佳方法是使用复数运算重写 LUdcmp。在构造缩放向量 vv 以及寻找最大主元时，用复数模代替绝对值。其余部分则自然地使用复数算术进行处理。

另一种快速但粗糙的方法是将式 (2.3.16) 的实部与虚部分开，得到：

$$\begin{array}{r}\mathbf{A}\cdot \mathbf{x}-\mathbf{C}\cdot \mathbf{y}=\mathbf{b}\\ \mathbf{C}\cdot \mathbf{x}+\mathbf{A}\cdot \mathbf{v}=\mathbf{d}\end{array}$$

这可以写成一个 $2N\times 2N$ 的实数方程组：

$$\left(\begin{array}{cc}\mathbf{A}& -\mathbf{C}\\ \mathbf{C}& \mathbf{A}\end{array}\right)\cdot \left(\begin{array}{c}\mathbf{x}\\ \mathbf{y}\end{array}\right)=\left(\begin{array}{c}\mathbf{b}\\ \mathbf{d}\end{array}\right)$$

然后直接使用现有的 LUdcmp 例程进行求解。这种方法在存储上效率降低了一半，因为 $\mathbf{A}$ 和 $\mathbf{C}$ 被存储了两次；在计算时间上也降低了一半，因为复数乘法在复数版本的例程中每次需要 4 次实数乘法，而求解一个 $2N\times 2N$ 的问题所需的工作量是求解 $N\times N$ 问题的 8 倍。如果你能接受这种两倍的低效，那么式 (2.3.18) 就是一种简便的处理方式。

参考文献

Golub, G.H., and Van Loan, C.F. 1996, Matrix Computations, 3rd ed. (Baltimore: Johns Hopkins University Press), Chapter 4.[1]

Anderson, E., et al. 1999, LAPACK User's Guide, 3rd ed. (Philadelphia: S.I.A.M.). Online with software at 2007+, http://www.netlib.org/lapack.

Forsythe, G.E., Malcolm, M.A., and Moler, C.B. 1977, Computer Methods for Mathematical Computations (Englewood Cliffs, NJ: Prentice-Hall), §3.3, and p. 50.

Forsythe, G.E., and Moler, C.B. 1967, Computer Solution of Linear Algebraic Systems (Englewood Cliffs, NJ: Prentice-Hall), Chapters 9, 16, and 18.

Westlake, J.R. 1968, A Handbook of Numerical Matrix Inversion and Solution of Linear Equations (New York: Wiley).

Stoer, J., and Bulirsch, R. 2002, Introduction to Numerical Analysis, 3rd ed. (New York: Springer), §4.1.

Ralston, A., and Rabinowitz, P. 1978, A First Course in Numerical Analysis, 2nd ed.; reprinted 2001 (New York: Dover), §9.11.

Horn, R.A., and Johnson, C.R. 1985, Matrix Analysis (Cambridge: Cambridge University Press).

2.4 三对角与带状对角方程组

线性方程组中一种常见特殊情况是三对角系统，即非零元素仅出现在主对角线及其上下相邻的一列上。另一种常见情况是带状对角系统，其非零元素仅出现在主对角线附近几条对角线上（主对角线上方和下方）。

对于三对角矩阵，$LU$ 分解、前向代入和回代这三个步骤各自仅需 $O(N)$ 次运算，整个求解过程可以非常简洁地编码。由此得到的子程序 tridag 将在后续章节中使用。

自然地，我们不会为完整的 $N\times N$ 矩阵分配存储空间，而仅存储非零元素，这些元素以三个向量的形式保存。待求解的方程组为：

$$\left[\begin{array}{llllllc}{b}_0& c_0& 0& \cdots & 0& 0& \\ a_1& b_1& c_1& \cdots & 0& 0& \\ 0& a_2& b_2& \cdots & 0& 0& \\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮& \\ 0& 0& 0& \cdots & a_{N-2}& b_{N-2}& c_{N-2}\\ 0& 0& 0& \cdots & 0& a_{N-1}& b_{N-1}\end{array}\right]\cdot \left[\begin{array}{l}{u}_0\\ u_1\\ ⋮\\ u_{N-2}\\ u_{N-1}\end{array}\right]=\left[\begin{array}{l}{r}_0\\ r_1\\ ⋮\\ r_{N-2}\\ r_{N-1}\end{array}\right]$$

注意：$a_0$ 和 $c_{N-1}$ 是未定义的，后续的例程也不会引用它们。

tridag.h

void tridag(VecDoub_I &a, VecDoub_I &b, VecDoub_I &c, VecDoub_I &r, VecDoub_O &u);

求解由方程 (2.4.1) 给出的三对角线性方程组，得到向量 $u[\mathrm{0..}n-1]$。输入向量 $a[\mathrm{0..}n-1]$、$b[\mathrm{0..}n-1]$、$c[\mathrm{0..}n-1]$ 和 $r[\mathrm{0..}n-1]$ 不会被修改。

如果出现这种情况，你应该将方程组改写为一个 $N-1$ 阶的方程组，并直接消去 $u_1$。

分解与前向代入。

tridag 中没有使用选主元策略。正因如此，即使原始矩阵是非奇异的，tridag 仍可能失败：即使对于非奇异矩阵，也可能遇到零主元。但在实践中，这通常不是需要担心的问题。导致三对角线性方程组的问题通常具有额外的性质，可以保证 tridag 中的算法成功。例如，若满足

$$|b_j|>|a_j|+|c_j|j=0,\dots ,N-1$$

（称为对角占优），则可以证明该算法不会遇到零主元。

可以构造一些特殊例子，其中由于算法中缺乏选主元而导致数值不稳定。然而在实践中，这种不稳定性几乎从未遇到过——这与一般矩阵问题中选主元至关重要形成鲜明对比。

三对角算法是少数几种在实践中比理论预期更为稳健的算法之一。当然，如果你确实遇到了 tridag 失败的问题，可以改用下面描述的更通用的带状对角系统求解方法（Bandec 对象）。

还有一些其他矩阵形式，它们在三对角的基础上仅增加少量额外元素（例如右上角和左下角），也可以快速求解；参见 §2.7。

2.4.1 三对角系统的并行求解

三对角系统可以在许多操作上实现并行求解。我们以 $N=7$ 的特例进行说明：

$$\left[\begin{array}{lllllll}{b}_0& c_0& 0& 0& 0& 0& 0\\ a_1& b_1& c_1& 0& 0& 0& 0\\ 0& a_2& b_2& c_2& 0& 0& 0\\ 0& 0& a_3& b_3& c_3& 0& 0\\ 0& 0& 0& a_4& b_4& c_4& 0\\ 0& 0& 0& 0& a_5& b_5& c_5\\ 0& 0& 0& 0& 0& a_6& b_6\end{array}\right]\cdot \left[\begin{array}{l}{u}_0\\ u_1\\ u_2\\ u_3\\ u_4\\ u_5\\ u_6\end{array}\right]=\left[\begin{array}{l}{r}_0\\ r_1\\ r_2\\ r_3\\ r_4\\ r_5\\ r_6\end{array}\right]$$

基本思想是将问题划分为偶数和奇数索引的元素，递归求解后者，然后并行求解前者。具体来说，我们首先通过置换方程 (2.4.3) 的行和列，将其重写为：

$$\left[\begin{array}{ccccccc}{b}_0& 0& c_0& 0& 0& 0& 0\\ 0& b_2& a_2& c_2& 0& 0& 0\\ 0& 0& b_4& a_4& c_4& 0& 0\\ 0& 0& 0& b_6& a_6& 0& 0\\ a_1& c_1& 0& 0& 0& b_1& 0\\ 0& a_3& c_3& 0& 0& 0& b_3\\ 0& 0& a_5& c_5& 0& 0& 0\end{array}\right]\cdot \left[\begin{array}{l}{u}_0\\ u_2\\ u_4\\ u_6\\ u_1\\ u_3\\ u_5\end{array}\right]=\left[\begin{array}{l}{r}_0\\ r_2\\ r_4\\ r_6\\ r_1\\ r_3\\ r_5\end{array}\right]$$

现在观察到，通过对最后三行分别减去前四行的适当倍数，我们可以将左下象限的所有非零元素消去。代价是在右下象限引入了一些新元素，我们将这些非零元素记为 $x$、$y$ 和 $z$。同时，我们将修改后的右侧向量记为 $q$。变换后的问题变为：

$$\left[\begin{array}{cccc}{b}_0& c_0& 0& 0\\ a_2& b_2& c_2& 0\\ 0& a_4& b_4& c_4\\ 0& 0& a_6& b_6\end{array}\right]\cdot \left[\begin{array}{c}{u}_0\\ u_2\\ u_4\\ u_6\end{array}\right]=\left[\begin{array}{c}{r}_0\\ r_2\\ r_4\\ r_6\end{array}\right]$$

$$\left[\begin{array}{ccc}{y}_0& x_1& z_1\\ x_2& y_2& z_2\\ 0& x_3& y_3\end{array}\right]\cdot \left[\begin{array}{c}{u}_1\\ u_3\\ u_5\end{array}\right]=\left[\begin{array}{c}{q}_0\\ q_1\\ q_2\end{array}\right]$$

注意到最后三行构成了一个新的、更小的三对角问题，我们可以简单地通过递归求解。一旦其解已知，前四行就可以通过一种简单且可并行化的代入方法求解。关于此方法及相关并行化三对角系统的其他方法的讨论及文献参考，见 [2]。

2.4.2 带状对角系统

三对角系统仅在主对角线及其上下各一条对角线上有非零元素，而带状对角系统则稍更一般：它在主对角线左侧（下方）有 $m_1\ge 0$ 个非零元素，在右侧（上方）有 $m_2\ge 0$ 个非零元素。当然，只有当 $m_1$ 和 $m_2$ 都远小于 $N$ 时，这种分类才有意义。在这种情况下，通过 $LU$ 分解求解线性系统所需的时间和存储空间都远少于一般的 $N\times N$ 情形。

带状对角矩阵（元素为 $a_{ij}$）的精确定义是：

$$a_{ij}=0\mathrm{当}j>i+m_2\mathrm{或}i>j+m_1$$

带状对角矩阵以所谓的紧凑形式存储和操作：将矩阵顺时针旋转 $45^{\circ }$，使其非零元素位于一个具有 $m_1+1+m_2$ 列和 $N$ 行的细长矩阵中。以下例子最能说明这一点：带状对角矩阵

$$\left(\begin{array}{lllllll}3& 1& 0& 0& 0& 0& 0\\ 4& 1& 5& 0& 0& 0& 0\\ 9& 2& 6& 5& 0& 0& 0\\ 0& 3& 5& 8& 9& 0& 0\\ 0& 0& 7& 9& 3& 2& 0\\ 0& 0& 0& 3& 8& 4& 0\\ 0& 0& 0& 0& 2& 4& 0\end{array}\right)$$

其中 $N=7$，$m_1=2$，$m_2=1$，其紧凑存储形式为一个 $7\times 4$ 的矩阵：

$$\left(\begin{array}{llll}x& x& 3& 1\\ x& 4& 1& 5\\ 9& 2& 6& 5\\ 3& 5& 8& 9\\ 7& 9& 3& 2\\ 3& 8& 4& x\\ 2& 4& 4& x\end{array}\right)$$

此处 $x$ 表示紧凑格式中被浪费的空间元素；这些元素不会被任何操作引用，可以取任意值。注意，原矩阵的对角线出现在第 $m_1$ 列中，其左侧为次对角线元素，右侧为超对角线元素。

对以紧凑格式存储的带状对角矩阵最简单的操作是将其右乘一个向量。尽管该操作在算法上很简单，但你可能仍希望研究以下例程，以了解如何以有序的方式从紧凑存储格式中提取非零元素 $a_{ij}$。

void banmul(MatDoub_I &a, const Int m1, const Int m2, VecDoub_I &x, VecDoub_O &b)
// banded.h
// 矩阵乘法 b = A·x，其中 A 是带状对角矩阵，对角线下方有 m1 行，上方有 m2 行。
// 输入向量为 x[0..n-1]，输出向量为 b[0..n-1]。
// 数组 a[0..n-1][0..m1+m2] 按如下方式存储 A：
// 对角线元素位于 a[0..n-1][m1]。
// 次对角线元素位于 a[j..n-1][0..m1-1]，其中 j>0 且与每条次对角线上元素数量相适应。
// 超对角线元素位于 a[0..j][m1+1..m1+m2]，其中 j<n-1 且与每条超对角线上元素数量相适应。
{
    Int i, j, k, traploop, n = a.nrows();
    for (i = 0; i < n; i++) {
        k = i - m1;
        traploop = MIN(m1 + m2 + 1, Int(n - k));
        b[i] = 0.0;
        for (j = MAX(0, -k); j < traploop; j++) b[i] += a[i][j] * x[j + k];
    }
}

无法将带状对角矩阵 $\mathbf{A}$ 的 $LU$ 分解以与 $\mathbf{A}$ 本身紧凑格式完全相同的紧凑程度进行存储。该分解（本质上采用 Crout 方法；参见 §2.3）会产生额外的非零“填充项”。一种直接的存储方案是：将上三角因子（$U$）存储在一个与 $\mathbf{A}$ 形状相同的空间中，而将下三角因子（$L$）存储在一个大小为 $N\times m_1$ 的独立紧凑矩阵中。$U$ 的对角线元素（其乘积乘以 $\mathrm{d}=\pm 1$ 即得行列式）位于 $U$ 的第一列中。

以下是与 §2.3 中 LUdcmp 类似的对象，用于求解带状对角线性方程组：

// banded.h
// 用于求解带状对角矩阵 A 的线性方程组 A·x = b，使用 LU 分解。
// 构造函数的参数为紧凑存储的矩阵 A 以及整数 m1 和 m2。
// （当然可以定义一个“带状对角矩阵对象”来封装这些量，
// 但在此简要讨论中，我们希望保持简单。）

Bandec::Bandec(MatDoub_I &a, const Int mm1, const Int mm2)
// banded.h
// : n(a.nrows()), au(a), m1(mm1), m2(mm2), al(n, m1), idx(n)
// 构造函数。给定一个 n×n 的带状对角矩阵 A，其有 m1 条次对角线和 m2 条超对角线，
// 并以如 banmul 例程注释所述的紧凑格式存储于数组 a[0..n-1][0..m1+m2] 中，
// 构造 A 的行置换后的 LU 分解。
// 上三角和下三角矩阵分别存储在 au 和 al 中。
// 存储的向量 idx[0..n-1] 记录了部分主元选取所引起的行置换；
// d 为 ±1，分别对应行交换次数为偶数或奇数。
{
    const Doub TINY = 1.0e-40;
    Int i, j, k, l, mm;
    Doub dum;
    mm = m1 + m2 + 1;
    l = m1;
    for (i = 0; i < m1; i++) {
        for (j = m1 - i; j < mm; j++) au[i][j - 1] = au[i][j];
        l--;
        for (j = mm - l - 1; j < mm; j++) au[i][j] = 0.0;
    }

    d = 1.0;
    l = m1;
    for (k = 0; k < n; k++) {
        dum = au[k][0];
        i = k;
        if (l < n) l++;
        for (j = k + 1; j < l; j++) {
            // 寻找主元元素。
            if (abs(au[j][0]) > abs(dum)) {
                dum = au[j][0];
                i = j;
            }
        }
        idx[k] = i + 1;
        if (dum == 0.0) au[k][0] = TINY;
        // 矩阵在算法上是奇异的，但仍以 TINY 作为主元继续（在某些应用中是可取的）。
        if (i != k) {
            d = -d;
            for (j = 0; j < mm; j++) SWAP(au[k][j], au[i][j]);
        }
        for (i = k + 1; i < l; i++) {
            dum = au[i][0] / au[k][0];
            al[k][i - k - 1] = dum;
            for (j = 1; j < mm; j++) au[i][j - 1] = au[i][j] - dum * au[k][j];
            au[i][mm - 1] = 0.0;
        }
    }
}

在 Bandec 的存储限制内可以进行一定程度的主元选取，上述例程利用了这一机会。通常，当 $U$ 的对角线元素返回为 TINY 时，原始矩阵（可能受舍入误差影响）实际上是奇异的。在这方面，Bandec 比前面的 tridag 更加稳健，因为 tridag 即使对于非奇异矩阵也可能在算法上失败；因此，Bandec（当 $m_1=m_2=1$ 时）对于某些病态的三对角系统也很有用。

一旦矩阵 $\mathbf{A}$ 被分解，就可以通过反复调用 solve 方法来依次求解任意多个右端项，该方法是前代和回代例程，与 §2.3 中同名例程类似。

void Bandec::solve(VecDoub_I &b, VecDoub_O &x)
// 给定右端向量 b[0..n-1]，求解带状对角线性方程组 A·x = b。
// 解向量 x 以 x[0..n-1] 的形式返回。
{
    Int i, j, k, l, mm;
    Doub dum;
    mm = m1 + m2 + 1;
    l = m1;
    for (k = 0; k < n; k++) x[k] = b[k];
    for (k = 0; k < n; k++) {
        j = idx[k] - 1;
        if (j != k) SWAP(x[k], x[j]);
        if (l < n) l++;
        for (j = k + 1; j < l; j++) x[j] -= al[k][j - k - 1] * x[k];
    }
    l = 1;
    for (i = n - 1; i >= 0; i--) {
        dum = x[i];
        for (k = 1; k < l; k++) dum -= au[i][k] * x[k + i];
        x[i] = dum / au[i][0];
        if (l < mm) l++;
    }
}

最后，提供一个计算行列式的方法：

Doub Bandec::det() {
    // 利用已存储的分解结果，返回矩阵 A 的行列式。
    Doub dd = d;
    for (int i = 0; i < n; i++) dd *= au[i][0];
    return dd;
}

Bandec 中的例程基于文献 [1] 中的 Handbook 例程 bandet1 和 bansol1。

参考文献

Keller, H.B. 1968, Numerical Methods for Two-Point Boundary-Value Problems; reprinted 1991 (New York: Dover), p. 74.

Dahlquist, G., and Bjorck, A. 1974, Numerical Methods (Englewood Cliffs, NJ: Prentice-Hall); reprinted 2003 (New York: Dover), Example 5.4.3, p. 166.

Ralston, A., and Rabinowitz, P. 1978, A First Course in Numerical Analysis, 2nd ed.; reprinted 2001 (New York: Dover), §9.11.

Wilkinson, J.H., and Reinsch, C. 1971, Linear Algebra, vol. II of Handbook for Automatic Computation (New York: Springer), Chapter I/6.[1]

Golub, G.H., and Van Loan, C.F. 1996, Matrix Computations, 3rd ed. (Baltimore: Johns Hopkins University Press), §4.3.

Hockney, R.W., 和 Jesshope, C.R. 1988，《并行计算机 2：体系结构、编程与算法》（布里斯托尔和费城：Adam Hilger），§5.4。[2]

2.5 线性方程组解的迭代改进

显然，线性方程组解的精度不可能超过计算机浮点字长的精度。不幸的是，对于大型线性方程组，有时甚至难以获得与计算机精度极限相等或相近的精度。在直接解法中，舍入误差会累积，并且当矩阵接近奇异时，这些误差会被放大。即使你认为矩阵离奇异还很远，也可能轻易损失两到三位有效数字。

如果你遇到这种情况，有一种巧妙的方法可以恢复完整的机器精度，称为解的迭代改进。其理论非常直接（见图 2.5.1）：假设向量 $\mathbf{x}$ 是线性方程组

$$\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$$

的精确解。

然而，你并不知道 $\mathbf{x}$，只知道某个稍有偏差的解 $\mathbf{x}+\delta \mathbf{x}$，其中 $\delta \mathbf{x}$ 是未知的误差。将这个稍有偏差的解乘以矩阵 $\mathbf{A}$，会得到一个与期望右端项 $\mathbf{b}$ 稍有偏差的结果，即

$$\mathbf{A}\cdot (\mathbf{x}+\delta \mathbf{x})=\mathbf{b}+\delta \mathbf{b}$$

用 (2.5.2) 减去 (2.5.1) 得到

$$\mathbf{A}\cdot \delta \mathbf{x}=\delta \mathbf{b}$$

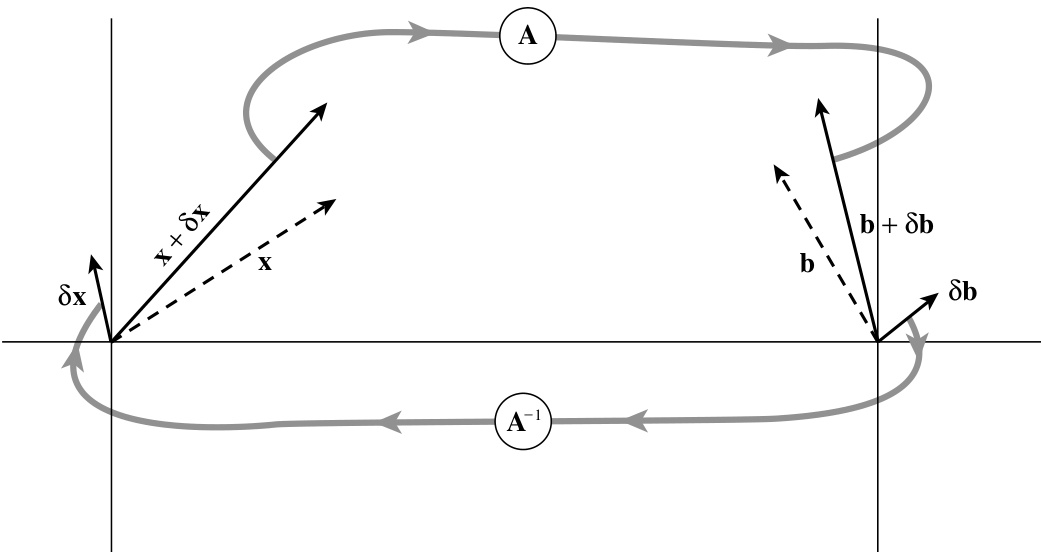
图 2.5.1. 对 $\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$ 的解进行迭代改进。初始猜测 $\mathbf{x}+\delta \mathbf{x}$ 乘以 $\mathbf{A}$ 得到 $\mathbf{b}+\delta \mathbf{b}$。减去已知向量 $\mathbf{b}$，得到 $\delta \mathbf{b}$。以该右端项求解线性方程组，得到 $\delta \mathbf{x}$。将其从初始猜测中减去，得到改进后的解 $\mathbf{x}$。

但 (2.5.2) 也可以直接解出 $\delta \mathbf{b}$。将其代入 (2.5.3) 得到

$$\mathbf{A}\cdot \delta \mathbf{x}=\mathbf{A}\cdot (\mathbf{x}+\delta \mathbf{x})-\mathbf{b}$$

在此方程中，右边是完全已知的，因为 $\mathbf{x}+\delta \mathbf{x}$ 正是你希望改进的错误解。如果可能的话，最好以比原始解更高的精度计算右边，因为在 $\mathbf{b}$ 的减法过程中会出现大量抵消。然后，我们只需解 (2.5.4) 得到误差 $\delta \mathbf{x}$，再将其从错误解中减去，即可得到改进后的解。

如果我们通过 $LU$ 分解得到了原始解，那么还有一个重要的额外好处。在这种情况下，我们已经拥有矩阵 $\mathbf{A}$ 的 $LU$ 分解形式，因此解 (2.5.4) 所需做的只是计算右边项，然后进行前代和回代。

由于 LUdcmp 中已经包含了大量必要的机制，我们将迭代改进实现为该类的一个成员函数。由于迭代改进需要矩阵 $\mathbf{A}$（及其 $LU$ 分解），我们事先已让 LUdcmp 保存对其构造所用矩阵 $\mathbf{a}$ 的引用。如果你计划使用迭代改进，则不得修改 $\mathbf{a}$ 或使其超出作用域。（LUdcmp 中的其他方法均未使用此对 $\mathbf{a}$ 的引用。）

void LUdcmp::mprove(VecDoub_I &b, VecDoub_IO &x)

改进线性方程组 $\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$ 的解向量 $\mathbf{x}[\mathrm{0..}n-1]$。输入向量 $\mathbf{b}[\mathrm{0..}n-1]$ 和 $\mathbf{x}[\mathrm{0..}n-1]$。输出时，$\mathbf{x}[\mathrm{0..}n-1]$ 被修改为一组改进后的值。

{
    Int i,j;
    VecDoub r(n);
    for (i=0;i<n;i++) {
        Ldoub sdp = -b[i];
        for (j=0;j<n;j++) {
            sdp += (Ldoub)aref[i][j] * (Ldoub)x[j];
        }
        r[i]=sdp;
    }
    solve(r,r);
    for (i=0;i<n;i++) x[i] -= r[i];
}

强烈推荐使用迭代改进：它仅需 $N^2$ 阶运算（向量乘矩阵、前代和回代——参见 2.3.7 式后的讨论）；它绝不会带来负面影响；而且如果它能挽救一个原本因舍入误差而失效的解（而你已在该解上花费了 $N^3$ 阶的运算），那么它将物超所值。

如果你愿意，可以连续多次调用 mprove。除非初始解离真实解非常远，通常一次调用就足够了；但第二次调用以验证收敛性会让人更放心。

如果你无法以更高精度计算 (2.5.4) 式中的右端项，迭代改进通常仍能改善解的质量，尽管在某些情况下效果不如使用更高精度时显著。许多教科书持相反观点，但你可以在 [1] 中找到证明。

2.5.1 关于迭代改进的进一步讨论

为 (2.5.4) 式提供一个更坚实的分析基础（这在本书后续内容中也会有用），并给出一些附加结果，是很有启发性的。前面的讨论隐含了这样一个概念：解向量 $\mathbf{x}+\delta \mathbf{x}$ 包含一个误差项；但我们忽略了 $\mathbf{A}$ 的 $LU$ 分解本身也不是精确的这一事实。

另一种分析方法从某个矩阵 ${\mathbf{B}}_0$ 出发，假设它是矩阵 $\mathbf{A}$ 的近似逆，因此 ${\mathbf{B}}_0\cdot \mathbf{A}$ 近似于单位矩阵 $1$。定义 ${\mathbf{B}}_0$ 的残差矩阵 $\mathbf{R}$ 为

$$\mathbf{R}\equiv 1-{\mathbf{B}}_0\cdot \mathbf{A}$$

它被认为是“小”的（我们稍后会更精确地说明）。注意，因此有

$${\mathbf{B}}_0\cdot \mathbf{A}=1-\mathbf{R}$$

接下来考虑以下形式化操作：

$$\begin{array}{r}{\mathbf{A}}^{-1}={\mathbf{A}}^{-1}\cdot ({\mathbf{B}}_0^{-1}\cdot {\mathbf{B}}_0)=({\mathbf{A}}^{-1}\cdot {\mathbf{B}}_0^{-1})\cdot {\mathbf{B}}_0=({\mathbf{B}}_0\cdot \mathbf{A}{)}^{-1}\cdot {\mathbf{B}}_0\\ =(1-\mathbf{R}{)}^{-1}\cdot {\mathbf{B}}_0=(1+\mathbf{R}+{\mathbf{R}}^2+{\mathbf{R}}^3+\cdots )\cdot {\mathbf{B}}_0\end{array}$$

我们可以将最后一个表达式的第 $n$ 项部分和定义为

$${\mathbf{B}}_n\equiv (1+\mathbf{R}+\cdots +{\mathbf{R}}^n)\cdot {\mathbf{B}}_0$$

使得若极限存在，则有 ${\mathbf{B}}_{\infty }\to {\mathbf{A}}^{-1}$。

现在很容易验证方程 (2.5.8) 满足一些有趣的递推关系。关于求解线性方程组 $A\cdot x=b$（其中 $x$ 和 $b$ 为向量），定义

$${\mathbf{x}}_n\equiv {\mathbf{B}}_n\cdot \mathbf{b}$$

则很容易证明

$${\mathbf{x}}_{n+1}={\mathbf{x}}_n+{\mathbf{B}}_0\cdot (\mathbf{b}-\mathbf{A}\cdot {\mathbf{x}}_n)$$

这显然就是方程 (2.5.4)，其中 $-\delta \mathbf{x}={\mathbf{x}}_{n+1}-{\mathbf{x}}_n$，且 ${\mathbf{B}}_0$ 扮演了 ${\mathbf{A}}^{-1}$ 的角色。因此我们看到，方程 (2.5.4) 并不要求 $\mathbf{A}$ 的 $LU$ 分解是精确的，而仅要求隐含的残差 $\mathbf{R}$ 足够小。粗略地说，

如果残差小于计算机舍入误差的平方根，那么在应用一次方程 (2.5.10)（即从 ${\mathbf{x}}_0\equiv {\mathbf{B}}_0\cdot \mathbf{b}$ 到 ${\mathbf{x}}_1$）之后，被忽略的首项（阶数为 ${\mathbf{R}}^2$）将小于舍入误差。此外，与方程 (2.5.4) 类似，方程 (2.5.10) 也可以多次应用，因为它仅使用 ${\mathbf{B}}_0$，而不涉及更高阶的 $\mathbf{B}$。

从方程 (2.5.8) 还可以导出一个更令人惊讶的递推关系，它在每一步都将阶数 $n$ 提升一倍以上：

$${\mathbf{B}}_{2n+1}=2{\mathbf{B}}_n-{\mathbf{B}}_n\cdot \mathbf{A}\cdot {\mathbf{B}}_{n}n=0,1,3,7,\dots$$

从一个合适的初始矩阵 ${\mathbf{B}}_0$ 出发，反复应用方程 (2.5.11) 将以二次收敛速度逼近未知的逆矩阵 ${\mathbf{A}}^{-1}$（“二次收敛”的定义见 §9.4）。方程 (2.5.11) 有多种名称，包括 Schultz 方法和 Hotelling 方法；参见 Pan 和 Reif [2] 的参考文献。事实上，方程 (2.5.11) 本质上就是用于求根的 Newton-Raphson 迭代法（见 §9.4）在矩阵求逆问题上的直接应用。

然而，在你对方程 (2.5.11) 过于兴奋之前，应注意它在每次迭代中都涉及两次完整的矩阵乘法。每次矩阵乘法都需要 $N^3$ 次加法和乘法运算。但我们在 §2.1–§2.3 中已经看到，直接求逆 $\mathbf{A}$ 总共只需要 $N^3$ 次加法和 $N^3$ 次乘法。因此，只有当特殊情形使得方程 (2.5.11) 的计算速度远快于一般矩阵时，该方法才是实用的。我们将在 §13.10 中遇到这样的情况。

本着延迟满足的精神，我们仍继续探讨两个相关问题：方程 (2.5.7) 中的级数何时收敛？以及什么样的初始猜测 ${\mathbf{B}}_0$ 是合适的（例如，当初始的 $LU$ 分解不可行时）？

我们可以将矩阵的范数定义为它对任意向量所能引起的最大长度放大倍数：

$$\Vert \mathbf{R}\Vert \equiv \underset{\mathbf{v}\ne 0}{\max }\frac{|\mathbf{R}\cdot \mathbf{v}|}{|\mathbf{v}|}$$

如果让方程 (2.5.7) 作用于某个任意的右端项 $\mathbf{b}$（这正是我们希望矩阵逆所做的事情），显然级数收敛的一个充分条件是

$$\Vert \mathbf{R}\Vert <1$$

Pan 和 Reif [2] 指出，${\mathbf{B}}_0$ 的一个合适初始猜测是取一个足够小的常数 $ϵ$ 乘以 $\mathbf{A}$ 的转置矩阵，即

$${\mathbf{B}}_0=ϵ{\mathbf{A}}^T\text{或}\mathbf{R}=1-ϵ{\mathbf{A}}^T\cdot \mathbf{A}$$

要理解这一点需要用到第 11 章的概念；这里仅给出最简要的说明：${\mathbf{A}}^T\cdot \mathbf{A}$ 是一个对称正定矩阵，因此具有实的正特征值。在其对角化表示下，$\mathbf{R}$ 具有如下形式：

$$\mathbf{R}=\mathrm{diag}(1-ϵ{\lambda }_0,1-ϵ{\lambda }_1,\dots ,1-ϵ{\lambda }_{N-1})$$

其中所有 ${\lambda }_i$ 均为正数。显然，任何满足 $0<ϵ<2/({\max }_i{\lambda }_i)$ 的 $ϵ$ 都将保证 $\Vert \mathbf{R}\Vert <1$。不难证明，使方程 (2.5.11) 收敛最快的最优 $ϵ$ 为

$$ϵ=2/(\underset{i}{\max }{\lambda }_i+\underset{i}{\min }{\lambda }_i)$$

通常我们并不知道方程 (2.5.16) 中 ${\mathbf{A}}^T\cdot \mathbf{A}$ 的特征值。Pan 和 Reif 推导出了若干有趣的界，这些界可直接从 $\mathbf{A}$ 计算得到。以下选择可保证当 $n\to \infty$ 时 ${\mathbf{B}}_n$ 收敛：

$$ϵ\le 1/\sum _{j,k}{a}_{jk}^2\text{或}ϵ\le 1/(\underset{i}{\max }\sum _j|a_{ij}|\times \underset{j}{\max }\sum _i|a_{ij}|)$$

后一个表达式确实是一个非凡的公式，Pan 和 Reif 通过注意到方程 (2.5.12) 中的向量范数不必是通常的 $L_2$ 范数，而可以是 $L_{\infty }$（最大值）范数或 $L_1$（绝对值）范数而推导出该结果。详情请参见他们的工作。

另一种我们曾取得一定成功的方法是通过统计方式估计最大特征值：对若干个在 $N$ 维空间中随机方向的单位向量 ${\mathbf{v}}_i$，计算 $s_i\equiv |\mathbf{A}\cdot {\mathbf{v}}_i{|}^2$。然后最大特征值 $\lambda$ 可由 $\max (2\max s_i,2N\text{Var}(s_i)/\mu (s_i))$ 给出上界，其中 $\text{Var}$ 和 $\mu$ 分别表示样本方差和样本均值。

参考文献

Johnson, L.W., and Riess, R.D. 1982, Numerical Analysis, 2nd ed. (Reading, MA: Addison-Wesley), §2.3.4, p. 55.

Golub, G.H., and Van Loan, C.F. 1996, Matrix Computations, 3rd ed. (Baltimore: Johns Hopkins University Press), §3.5.3.

Dahlquist, G., and Bjorck, A. 1974, Numerical Methods (Englewood Cliffs, NJ: Prentice-Hall); reprinted 2003 (New York: Dover), §5.5.6, p. 183.

Forsythe, G.E., and Moler, C.B. 1967, Computer Solution of Linear Algebraic Systems (Englewood Cliffs, NJ: Prentice-Hall), Chapter 13.

Ralston, A., and Rabinowitz, P. 1978, A First Course in Numerical Analysis, 2nd ed.; reprinted 2001 (New York: Dover), §9.5, p. 437.

Higham, N.J. 1997, "Iterative Refinement for Linear Systems and LAPACK," IMA Journal of Numerical Analysis, vol. 17, pp. 495–509.[1]

Pan, V., and Reif, J. 1985, "Efficient Parallel Solution of Linear Systems," in Proceedings of the Seventeenth Annual ACM Symposium on Theory of Computing (New York: Association for Computing Machinery).[2]

2.6 奇异值分解

存在一套非常强大的技术，可用于处理奇异或数值上非常接近奇异的方程组或矩阵。在许多高斯消元法和 $LU$ 分解无法给出满意结果的情形下，这套被称为奇异值分解（Singular Value Decomposition, SVD）的技术能够精确地诊断出问题所在。在某些情况下，SVD不仅能诊断问题，还能解决问题——即给出一个有用的数值解，尽管如我们将看到的，这个解未必是你原本期望得到的“那个”解。

SVD 也是求解大多数线性最小二乘问题的首选方法。我们将在本节概述相关理论，但将 SVD 在该应用中的详细讨论推迟到第 15 章，该章的主题是数据的参数建模。

SVD 方法基于线性代数中的如下定理，其证明超出了本书范围：任意 $M\times N$ 矩阵 $\mathbf{A}$ 都可以分解为一个 $M\times N$ 列正交矩阵 $\mathbf{U}$、一个 $N\times N$ 对角矩阵 $\mathbf{W}$（其对角元素为非负的奇异值）以及一个 $N\times N$ 正交矩阵 $\mathbf{V}$ 的转置的乘积。这些矩阵的不同形状通过表格形式展示会更清晰。若 $M>N$（即方程个数多于未知数的超定情形），分解形式如下：

$$\mathbf{A}=\mathbf{U}\cdot \left(\begin{array}{cccc}{w}_0& & & \\ & w_1& & \\ & & \ddots & \\ & & & w_{N-1}\end{array}\right)\cdot {\mathbf{V}}^T$$

若 $M<N$（即方程个数少于未知数的欠定情形），分解形式如下：

$$\mathbf{A}=\mathbf{U}\cdot \left(\begin{array}{cccc}{w}_0& & & \\ & w_1& & \\ & & \ddots & \\ & & & w_{M-1}\\ & & & \\ & & & \end{array}\right)\cdot {\mathbf{V}}^T$$

矩阵 $\mathbf{V}$ 是正交的，即其列向量是标准正交的：

$$\sum _{i=0}^{N-1}{V}_{ik}{V}_{in}={\delta }_{kn}\begin{array}{l}0\le k\le N-1\\ 0\le n\le N-1\end{array}$$

即 ${\mathbf{V}}^T\cdot \mathbf{V}=\mathbf{I}$。由于 $\mathbf{V}$ 是方阵，其行向量也是标准正交的，即 $\mathbf{V}\cdot {\mathbf{V}}^T=\mathbf{I}$。

当 $M\ge N$ 时，矩阵 $\mathbf{U}$ 也是列正交的：

$$\sum _{i=0}^{M-1}{U}_{ik}{U}_{in}={\delta }_{kn}\begin{array}{l}0\le k\le N-1\\ 0\le n\le N-1\end{array}$$

即 ${\mathbf{U}}^T\cdot \mathbf{U}=\mathbf{I}$。然而，当 $M<N$ 时，会发生两件事：(i) 对于 $j=M,\dots ,N-1$，奇异值 $w_j$ 全为零；(ii) $\mathbf{U}$ 中对应的列也为零。此时，式 (2.6.4) 仅对 $k,n\le M-1$ 成立。

分解式 (2.6.1) 或 (2.6.2) 总是可以实现的，无论矩阵多么奇异，且该分解“几乎”是唯一的。也就是说，其唯一性允许以下两种操作：(i) 对 $\mathbf{U}$ 的列、$\mathbf{W}$ 的元素以及 $\mathbf{V}$ 的列（或 ${\mathbf{V}}^T$ 的行）进行相同的置换；(ii) 对 $\mathbf{W}$ 中对应元素恰好相等的 $\mathbf{U}$ 和 $\mathbf{V}$ 的任意列集进行正交旋转。（一个特例是将 $\mathbf{U}$ 的任意一列及其对应的 $\mathbf{V}$ 列同时乘以 $-1$。）由于置换自由度的存在，在 $M<N$ 的情形下，数值算法返回的零奇异值 $w_j$ 不一定位于标准位置 $j=M,\dots ,N-1$；这 $N-M$ 个零奇异值可能散布在所有位置 $j=0,1,\dots ,N-1$ 中，因此需要进行排序以获得标准顺序。无论如何，通常习惯将所有奇异值按降序排列。

一篇网络附注 [1] 给出了实际对任意矩阵 $\mathbf{A}$ 执行 SVD 并得到 $\mathbf{U}$、$\mathbf{W}$ 和 $\mathbf{V}$ 的例程细节。该例程基于 Forsythe 等人 [2] 的例程，而后者又基于 Golub 和 Reinsch 的原始例程，该例程以不同形式出现在 [4–6] 及其他文献中。这些参考文献对所用算法有详尽讨论。尽管我们通常不喜欢使用黑箱例程，但此处不得不请您接受这一例程，因为在此详述其所需背景知识会偏离主题太远。该算法非常稳定，极少出现异常行为。算法中涉及的多数概念（如 Householder 变换化为双对角形式、带位移的 $QR$ 过程对角化等）将在第 11 章进一步讨论。

与 $LU$ 分解类似，我们将奇异值分解及其相关方法封装到一个名为 SVD 的对象中。此处给出其声明，本节其余部分将详细介绍如何使用它。

struct SVD {
    // 用于矩阵 A 的奇异值分解及相关函数的对象。
    Int m, n;
    MatDoub u, v;
    VecDoub w;
    Doub eps, tsh;

    SVD(MatDoub_I &a) : m(a.nrows()), n(a.ncols()), u(a), v(n, n), w(n) {
        // 构造函数。唯一参数是 A。SVD 计算由 decompose 完成，结果由 reorder 排序。
        eps = numeric_limits<Doub>::epsilon();
        decompose();
        reorder();
        tsh = 0.5 * sqrt(m + n + 1) * w[0] * eps;
    }

    void solve(VecDoub_I &b, VecDoub_O &x, Doub thresh);
    void solve(MatDoub_I &b, MatDoub_O &x, Doub thresh);
    // 对一个或多个右端项求解（应用伪逆）。

    Int rank(Doub thresh);
    Int nullity(Doub thresh);
    MatDoub range(Doub thresh);
    MatDoub nullspace(Doub thresh);

    Doub inv_condition() {
        return (w[0] <= 0. || w[n-1] <= 0.) ? 0. : w[n-1] / w[0]; // A 的条件数的倒数。
    }

    void decompose();
    void reorder();
    Doub pythag(const Doub a, const Doub b);
};

2.6.1 值域、零空间及其他相关概念

考虑熟悉的联立方程组：

$$\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$$

其中 $\mathbf{A}$ 是一个 $M\times N$ 矩阵，$\mathbf{x}$ 和 $\mathbf{b}$ 分别是 $N$ 维和 $M$ 维向量。式 (2.6.5) 将 $\mathbf{A}$ 定义为从 $N$ 维向量空间到（通常为）$M$ 维向量空间的线性映射。但该映射可能只能到达 $M$ 维空间的一个低维子空间，该子空间称为 $\mathbf{A}$ 的值域（range）。值域的维数称为 $\mathbf{A}$ 的秩（rank）。$\mathbf{A}$ 的秩等于其线性无关列的数目，也（或许不那么显然地）等于其线性无关行的数目。若 $\mathbf{A}$ 不全为零，则其秩至少为 1，至多为 $\min (M,N)$。

有时存在非零向量 $\mathbf{x}$ 使得 $\mathbf{A}\cdot \mathbf{x}=0$，即被 $\mathbf{A}$ 映射为零。所有此类向量构成的空间（$\mathbf{x}$ 所在的 $N$ 维空间的一个子空间）称为 $\mathbf{A}$ 的零空间（nullspace），其维数称为 $\mathbf{A}$ 的零度（nullity）。零度的取值范围为 0 到 $N$。秩-零度定理指出，对任意 $\mathbf{A}$，其秩与零度之和等于 $N$（即列数）。

一个重要的特殊情况是 $M=N$，此时 $\mathbf{A}$ 是一个 $N\times N$ 的方阵。如果 $\mathbf{A}$ 的秩为 $N$（即其可能的最大值），那么 $\mathbf{A}$ 是非奇异且可逆的：对于任意 $\mathbf{b}$，方程 $\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$ 都有唯一解，并且只有零向量被映射为零。在这种情况下，通常首选使用 $LU$ 分解（§2.3）来求解 $\mathbf{x}$。然而，如果 $\mathbf{A}$ 的秩小于 $N$（即零度大于零），则会发生两件事：(i) 对于大多数右端向量 $\mathbf{b}$，方程无解；(ii) 但某些 $\mathbf{b}$ 会有多个解（实际上是一整个子空间的解）。我们将在下文进一步讨论这种情况。

这一切与奇异值分解（SVD）有什么关系呢？SVD 显式地为矩阵的零空间和值域构造了标准正交基！具体来说，$\mathbf{U}$ 中对应非零奇异值 $w_j$ 的列向量构成值域的一组标准正交基；而 $\mathbf{V}$ 中对应零奇异值 $w_j$ 的列向量则构成零空间的一组标准正交基。我们的 SVD 对象提供了返回矩阵秩或零度（整数）的方法，同时也提供了返回值域和零空间的方法，这些子空间均以矩阵形式返回，其列向量构成对应子空间的标准正交基。

在将小于阈值 thresh 的奇异值置零后，返回 $\mathbf{A}$ 的零度。默认阈值如上所述。

以返回矩阵的列向量形式给出 $\mathbf{A}$ 值域的一组标准正交基。阈值 thresh 同上。

Int i, j, nr = 0;
MatDoub rnge(m, rank(thresh));
for (j = 0; j < n; j++) {
    if (w[j] > tsh) {
        for (i = 0; i < m; i++) rnge[i][nr] = u[i][j];
        nr++;
    }
}
return rnge;

MatDoub SVD::nullspace(Doub thresh = -1) {
    // 以返回矩阵的列向量形式给出 A 零空间的一组标准正交基。阈值 thresh 同上。
    Int j, jj, nn = 0;
    MatDoub nullsp(n, nullity(thresh));
    for (j = 0; j < n; j++) {
        if (w[j] <= tsh) {
            for (jj = 0; jj < n; jj++) nullsp[jj][nn] = v[jj][j];
            nn++;
        }
    }
    return nullsp;
}

可选参数 thresh 的含义将在下文讨论。

2.6.2 方阵的奇异值分解

我们回到 $N\times N$ 方阵 $\mathbf{A}$ 的情形。此时 $\mathbf{U}$、$\mathbf{V}$ 和 $\mathbf{W}$ 也是同样大小的方阵。它们的逆矩阵也很容易计算：$\mathbf{U}$ 和 $\mathbf{V}$ 是正交矩阵，因此它们的逆等于它们的转置；$\mathbf{W}$ 是对角矩阵，其逆矩阵即为对角元素取倒数后的对角矩阵。由 (2.6.1) 式可立即得出 $\mathbf{A}$ 的逆矩阵为：

$${\mathbf{A}}^{-1}=\mathbf{V}\cdot \left[\mathrm{diag}\left(1/w_i\right)\right]\cdot {\mathbf{U}}^T$$

这种构造唯一可能出现的问题是某个 $w_j$ 为零，或者（在数值计算中）其值过小以至于被舍入误差所主导，从而无法准确获知。如果有多个 $w_j$ 出现此问题，则矩阵更加奇异。因此，SVD 首先能清晰地诊断出这种情况。

形式上，矩阵的条件数定义为其最大奇异值（绝对值）与最小奇异值之比。若条件数为无穷大，则矩阵是奇异的；若条件数过大（即其倒数接近机器浮点精度，例如对于 double 类型小于约 $10^{-15}$），则称矩阵是病态的。SVD 中实现了一个返回条件数（更准确地说，是其倒数，以避免溢出）的函数。

现在我们再来看看当 $\mathbf{A}$ 奇异时如何求解线性方程组 (2.6.5)。我们已经知道，对于齐次方程组（即 $\mathbf{b}=0$），SVD 可立即给出解：即上述 nullspace 方法返回的列向量的任意线性组合。

当右端向量 $\mathbf{b}$ 非零时，关键问题是 $\mathbf{b}$ 是否位于 $\mathbf{A}$ 的值域中。如果在，则该奇异方程组确实存在解 $\mathbf{x}$；事实上，它有无穷多个解，因为可以将零空间中的任意向量（即 $\mathbf{V}$ 中对应零奇异值 $w_j$ 的列向量）以任意线性组合加到 $\mathbf{x}$ 上。

如果我们希望从这个解集中选出一个特定的代表向量，可能会选择长度 $|\mathbf{x}{|}^2$ 最小的那个。使用 SVD 可按如下方式找到该向量：只需将 $1/w_j$ 在 $w_j=0$ 时替换为零。（这可是难得有机会将 $\infty =0$！）然后从右至左计算：

$$\mathbf{x}=\mathbf{V}\cdot \left[\mathrm{diag}\left(1/w_i\right)\right]\cdot ({\mathbf{U}}^T\cdot \mathbf{b})$$

该向量即为长度最小的解；$\mathbf{V}$ 中属于零空间的列向量则完整描述了整个解集。

证明：考虑 $|\mathbf{x}+{\mathbf{x}}^{\prime }|$，其中 ${\mathbf{x}}^{\prime }$ 属于零空间。若 ${\mathbf{W}}^{-1}$ 表示将 $\mathbf{W}$ 中某些元素置零后的修正逆矩阵，则有：

$$\begin{array}{rl}& \\ & \left|\mathbf{x}+{\mathbf{x}}^{\prime }\right|=\left|\mathbf{V}\cdot {\mathbf{W}}^{-1}\cdot {\mathbf{U}}^T\cdot \mathbf{b}+{\mathbf{x}}^{\prime }\right|\\ & =\left|\mathbf{V}\cdot ({\mathbf{W}}^{-1}\cdot {\mathbf{U}}^T\cdot \mathbf{b}+{\mathbf{V}}^T\cdot {\mathbf{x}}^{\prime })\right|\\ & =\left|{\mathbf{W}}^{-1}\cdot {\mathbf{U}}^T\cdot \mathbf{b}+{\mathbf{V}}^T\cdot {\mathbf{x}}^{\prime }\right|\end{array}$$

第一个等式来自 (2.6.7)，后两个等式则源于 $\mathbf{V}$ 的标准正交性。现在考察右侧和式中的两项：第一项仅在 $w_j\ne 0$ 处有非零分量，而第二项由于 ${\mathbf{x}}^{\prime }$ 属于零空间，仅在 $w_j=0$ 处有非零分量。因此，当 ${\mathbf{x}}^{\prime }=0$ 时长度最小，证毕。

如果 $\mathbf{b}$ 不在奇异矩阵 $\mathbf{A}$ 的值域中，则方程组 (2.6.5) 无解。但这里有个好消息：即使 $\mathbf{b}$ 不在 $\mathbf{A}$ 的值域中，仍可使用 (2.6.7) 式构造一个“解”向量 $\mathbf{x}$。该向量 $\mathbf{x}$ 虽不能精确满足 $\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$，但在所有可能的 $\mathbf{x}$ 中，它在最小二乘意义下是最优的。换句话说，(2.6.7) 式求得的是：

$$\mathbf{x}\text{使得}r\equiv |\mathbf{A}\cdot \mathbf{x}-\mathbf{b}|\text{最小}$$

该数值 $r$ 称为解的残差。

证明类似于 (2.6.8)：假设我们通过加上某个任意 ${\mathbf{x}}^{\prime }$ 来修改 $\mathbf{x}$，则 $\mathbf{A}\cdot \mathbf{x}-\mathbf{b}$ 将增加 ${\mathbf{b}}^{\prime }\equiv \mathbf{A}\cdot {\mathbf{x}}^{\prime }$。显然 ${\mathbf{b}}^{\prime }$ 属于 $\mathbf{A}$ 的值域。于是有：

$$\begin{array}{rl}& \left|\mathbf{A}\cdot \mathbf{x}-\mathbf{b}+{\mathbf{b}}^{\prime }\right|=\left|(\mathbf{U}\cdot \mathbf{W}\cdot {\mathbf{V}}^T)\cdot (\mathbf{V}\cdot {\mathbf{W}}^{-1}\cdot {\mathbf{U}}^T\cdot \mathbf{b})-\mathbf{b}+{\mathbf{b}}^{\prime }\right|\\ & =\left|(\mathbf{U}\cdot \mathbf{W}\cdot {\mathbf{W}}^{-1}\cdot {\mathbf{U}}^T-1)\cdot \mathbf{b}+{\mathbf{b}}^{\prime }\right|\\ & =\left|\mathbf{U}\cdot \left[(\mathbf{W}\cdot {\mathbf{W}}^{-1}-1)\cdot {\mathbf{U}}^T\cdot \mathbf{b}+{\mathbf{U}}^T\cdot {\mathbf{b}}^{\prime }\right]\right|\\ & =\left|(\mathbf{W}\cdot {\mathbf{W}}^{-1}-1)\cdot {\mathbf{U}}^T\cdot \mathbf{b}+{\mathbf{U}}^T\cdot {\mathbf{b}}^{\prime }\right|\end{array}$$

现在，$(\mathbf{W}\cdot {\mathbf{W}}^{-1}-1)$ 是一个对角矩阵，仅在 $w_j=0$ 处有非零分量；而 ${\mathbf{U}}^T{\mathbf{b}}^{\prime }$ 由于 ${\mathbf{b}}^{\prime }$ 属于 $\mathbf{A}$ 的值域，仅在 $w_j\ne 0$ 处有非零分量。因此，当 ${\mathbf{b}}^{\prime }=0$ 时取得最小值，证毕。

因此，(2.6.7) 式（同时也是结合律应用于 $\mathbf{b}$ 的 (2.6.6) 式）具有很强的普适性：若所有 $w_j$ 非零，则它求解一个非奇异线性方程组；若某些 $w_j$ 为零，并将其倒数置零，则它给出一个“最优”解——要么是众多解中长度最短者，要么是在无精确解时残差最小者。将奇异值 $1/w_j$ 置零后的 (2.6.6) 式称为 $\mathbf{A}$ 的 Moore-Penrose 逆或伪逆。

(2.6.7) 式在 SVD 对象中通过 solve 方法实现。（与 LUDcmp 类似，我们也提供了重载形式，可同时求解多个右端向量。）参数 thresh 输入一个阈值，低于该值的 $w_j$ 被视为零；若省略此参数或设为负值，则程序使用基于预期舍入误差的默认值。

void SVD::solve(VecDoub_I &b, VecDoub_O &x, Doub thresh = -1) {
    // 使用 SVD 得到的 A 的伪逆求解 A · x = b。
    // 若 thresh 为正，则作为判断奇异值是否为零的阈值；
    // 若 thresh 为负，则使用基于预期舍入误差的默认值。
}

Int i, j, jj;
Doub s;
if (b.size() != m || x.size() != n) throw("SVD::solve bad sizes");
VecDoub tmp(n);
tsh = (thresh >= 0. ? thresh : 0.5 * sqrt(m + n + 1.) * w[0] * eps);
for (j = 0; j < n; j++) {
    // 计算 $U^T B$。
    s = 0.0;
    if (w[j] > tsh) {
        // 仅当 $w_j$ 非零时才有非零结果。
        for (i = 0; i < m; i++) s += u[i][j] * b[i];
        s /= w[j];
    }
    tmp[j] = s;
}
for (j = 0; j < n; j++) {
    // 通过矩阵乘法乘以 $V$ 得到答案。
    s = 0.0;
    for (jj = 0; jj < n; jj++) s += v[j][jj] * tmp[jj];
    x[j] = s;
}

void SVD::solve(MatDoub_I &b, MatDoub_O &x, Doub thresh = -1.)
// 使用 A 的伪逆求解 m 组 n 元方程 A · X = B。
// 右端项以 b[0..n-1][0..m-1] 输入，解返回在 x[0..n-1][0..m-1] 中。
// thresh 含义同上。
{
    int i, j, m = b.ncols();
    if (b.nrows() != n || x.nrows() != n || b.ncols() != x.ncols())
        throw("SVD::solve bad sizes");
    VecDoub xx(n);
    for (j = 0; j < m; j++) {
        // 依次复制并求解每一列。
        for (i = 0; i < n; i++) xx[i] = b[i][j];
        solve(xx, xx, thresh);
        for (i = 0; i < n; i++) x[i][j] = xx[i];
    }
}

图 2.6.1 总结了方阵 SVD 的情形。

有时你可能希望将 thresh 的值设为大于其默认值。（你可以通过成员变量 tsh 获取默认值。）在式 (2.6.5) 之后的讨论中，我们一直假设矩阵要么奇异，要么非奇异。然而在数值计算中，更常见的情形是某些 $w_j$ 非常小但非零，导致矩阵病态。此时，LU 分解或高斯消元等直接解法可能确实给出方程组的形式解（即未遇到零主元）；但解向量可能包含极大分量，这些分量在与矩阵 $\mathbf{A}$ 相乘时通过代数相消，可能对右端向量 $\mathbf{b}$ 给出非常差的近似。在这种情况下，通过将小的 $w_j$ 置零后再使用式 (2.6.7) 得到的解向量 $\mathbf{x}$，通常比直接法解和保留小 $w_i$ 非零的 SVD 解更好（即残差 $|\mathbf{A}\cdot \mathbf{x}-\mathbf{b}|$ 更小）。

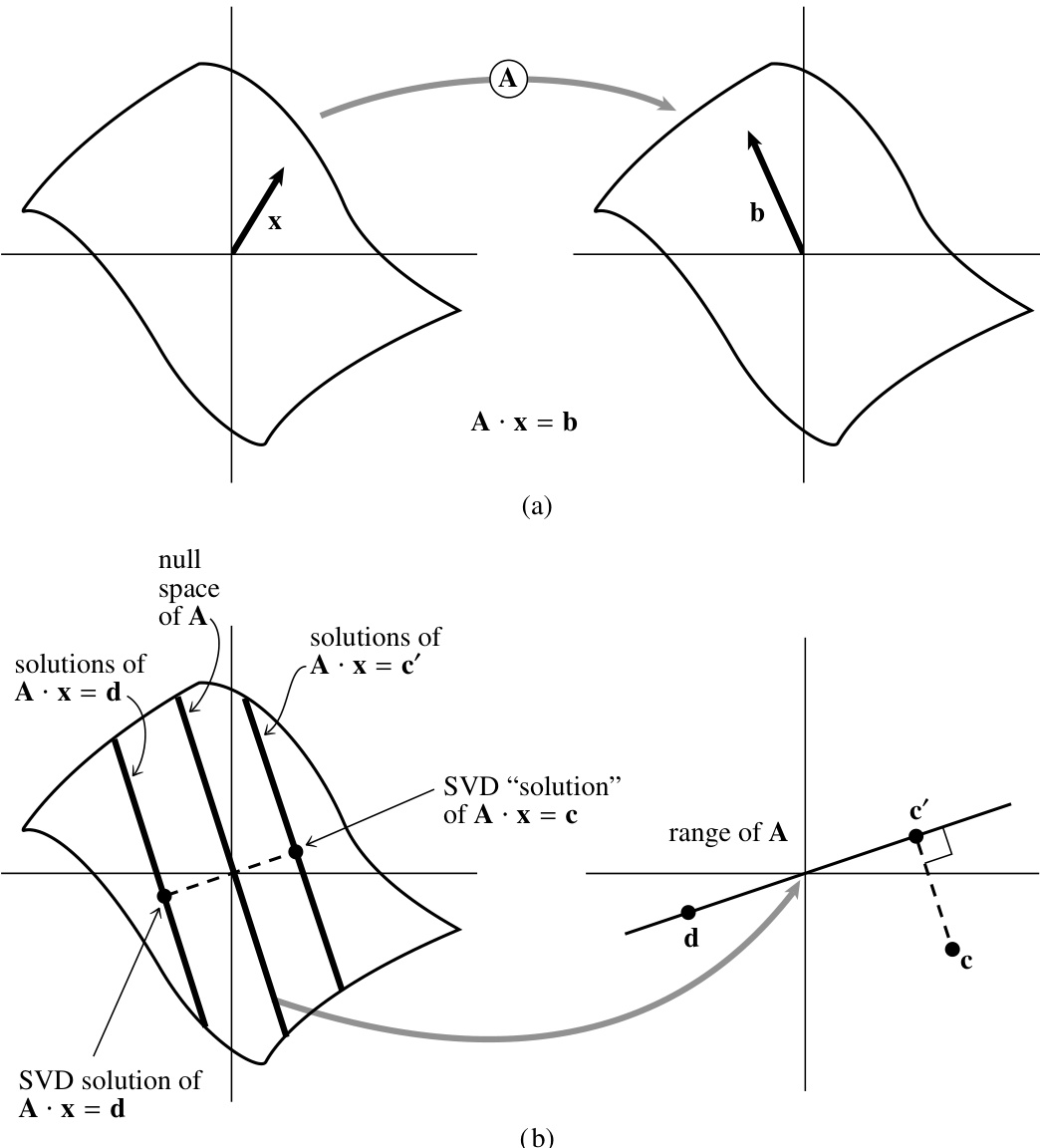
图 2.6.1. (a) 非奇异矩阵 $\mathbf{A}$ 将一个向量空间映射到同维空间。向量 $\mathbf{x}$ 被映射为 $\mathbf{b}$，因此 $\mathbf{x}$ 满足方程 $\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$。(b) 奇异矩阵 $\mathbf{A}$ 将一个向量空间映射到更低维空间，此处将一个平面映射为一条直线，称为 $\mathbf{A}$ 的“值域”。$\mathbf{A}$ 的“零空间”被映射为零。方程 $\mathbf{A}\cdot \mathbf{x}=\mathbf{d}$ 的解由任一特解加上零空间中的任意向量构成，此处形成一条与零空间平行的直线。奇异值分解（SVD）选择离零最近的特解，如图所示。点 $\mathbf{c}$ 位于 $\mathbf{A}$ 的值域之外，因此 $\mathbf{A}\cdot \mathbf{x}=\mathbf{c}$ 无解。SVD 找到最小二乘意义下的最佳折中解，即求解 $\mathbf{A}\cdot \mathbf{x}={\mathbf{c}}^{\prime }$，如图所示。

这看似矛盾，因为将一个奇异值置零相当于丢弃了我们试图求解的方程组中的一个线性组合。然而，这种矛盾的解释在于：我们丢弃的恰恰是被舍入误差严重污染、至多无用的方程组合；通常它比无用更糟，因为它会将解向量沿某个接近零空间向量的方向“拉”向无穷远。这样做会加剧舍入误差问题，使残差 $|\mathbf{A}\cdot \mathbf{x}-\mathbf{b}|$ 更大。

因此，你可以根据对可接受的计算残差 $|\mathbf{A}\cdot \mathbf{x}-\mathbf{b}|$ 大小的判断，自行决定在何种阈值下将小的 $w_j$ 置零。

关于矩阵的奇异值分解与其特征值和特征向量的关系，参见 §11.0.6。

2.6.3 未知数多于方程数的 SVD

若线性方程数 $M$ 少于未知数 $N$，则通常不期望得到唯一解。一般会有 $N-M$ 维的解族（即零度，假设无其他退化），但维数也可能更高。若你想找出整个解空间，SVD 可轻松完成此任务：用 solve 得到一个（最短）特解，再用 nullspace 得到零空间的一组基向量。你的通解即为该特解加上后者的任意线性组合。

2.6.4 未知数少于方程数的 SVD

这种情况将在第 15 章出现，当我们希望求超定线性方程组的最小二乘解时。用表格形式表示，待解方程为

$$\left(\begin{array}{c}\\ \\ \\ \end{array}\right)\cdot \left(\begin{array}{c}\\ \\ \\ \end{array}\right)=\left(\begin{array}{c}\\ \\ \\ \\ \end{array}\right)$$

前面针对方阵情形给出的证明可直接应用于未知数少于方程数的情形。最小二乘解向量 $\mathbf{x}$ 由伪逆 (2.6.7) 给出，对于非方阵，其形式如下：

$$\mathbf{x}=\mathbf{V}\cdot \mathrm{diag}(1/w_j)\cdot {\mathbf{U}}^T\cdot \mathbf{b}$$

通常矩阵 $\mathbf{W}$ 不会奇异，无需将任何 $w_j$ 置零。但偶尔 $\mathbf{A}$ 可能存在列退化。此时你仍需将某些小的 $w_j$ 置零。$\mathbf{V}$ 中对应的列给出了 $\mathbf{x}$ 的线性组合，即使在超定方程组下该组合仍无法确定。

有时，尽管出于计算原因无需置零任何 $w_j$，你仍可能关注那些异常小的 $w_j$：其对应的 $\mathbf{V}$ 列是 $\mathbf{x}$ 的线性组合，对你的数据不敏感。实际上，你可能希望通过增大 thresh 值来置零这些 $w_j$，以减少拟合中的自由参数数量。这些问题将在第 15 章详细讨论。

2.6.5 构造标准正交基

假设你在 $M$ 维向量空间中有 $N$ 个向量，且 $N\le M$。这 $N$ 个向量张成全空间的一个子空间。通常你希望构造一组 $N$ 个标准正交向量，使其张成相同的子空间。教科书中的基本方法是 Gram-Schmidt 正交化，从一个向量开始，逐维扩展子空间。然而，由于舍入误差的累积，朴素的 Gram-Schmidt 正交化在数值上效果极差。

构造子空间标准正交基的正确方法是使用 SVD：构造一个 $M\times N$ 矩阵 $\mathbf{A}$，其 $N$ 列即为你的向量。由该矩阵构造一个 SVD 对象。矩阵 $\mathbf{U}$ 的列即为你所需的标准正交基向量。

你还应检查 $w_j$ 是否有零值。若存在，则所张成的子空间实际上并非 $N$ 维；对应零 $w_j$ 的 $\mathbf{U}$ 列应从标准正交基中剔除。range 方法可完成此操作。

§2.10 讨论的 $QR$ 分解也能构造标准正交基；参见 [3]。

2.6.6 矩阵近似

注意式 (2.6.1) 可重写为将任意矩阵 $A_{ij}$ 表示为 $\mathbf{U}$ 的列与 ${\mathbf{V}}^T$ 的行的外积之和，其“权重因子”即为奇异值 $w_i$：

$$A_{ij}=\sum _{k=0}^{N-1}{w}_k{U}_{ik}{V}_{jk}$$

若你遇到矩阵 $\mathbf{A}$ 的大多数奇异值 $w_j$ 都非常小的情形，则 $\mathbf{A}$ 可由和式 (2.6.13) 中的少数几项很好地近似。这意味着你只需存储 $\mathbf{U}$ 和 $\mathbf{V}$ 的少数几列（相同的 $k$ 列），即可高精度地重构整个矩阵。

此外，用这样的近似矩阵乘以向量 $\mathbf{x}$ 非常高效：只需将 $\mathbf{x}$ 与每个存储的 $\mathbf{V}$ 列做点积，将结果标量乘以对应的 $w_k$，再累加对应 $\mathbf{U}$ 列的该倍数即可。若你的矩阵仅需 $K$ 个奇异值近似，则计算 $\mathbf{A}\cdot \mathbf{x}$ 仅需约 $K(M+N)$ 次乘法，而非完整矩阵的 $MN$ 次。

2.6.7 更新的算法

类似于§11.4.4中提到的对称三对角矩阵特征值的新方法，SVD（奇异值分解）也有新的方法。其中一种是分治算法（divide-and-conquer algorithm），在LAPACK中以dgesdd实现，对于大型矩阵，通常比我们给出的算法（类似于LAPACK例程dgesvd）快约5倍。另一种基于MRRR算法（参见§11.4.4）的例程有望表现更佳，但截至2006年尚未包含在LAPACK中，未来将以例程dbdscr的形式出现。

参考文献

Numerical Recipes Software 2007, "SVD Implementation Code," Numerical Recipes Webnote No. 2, at http://www.nr.com/webnotes?2 [1]

Forsythe, G.E., Malcolm, M.A., and Moler, C.B. 1977, Computer Methods for Mathematical Computations (Englewood Cliffs, NJ: Prentice-Hall), Chapter 9.[2]

Golub, G.H., and Van Loan, C.F. 1996, Matrix Computations, 3rd ed. (Baltimore: Johns Hopkins University Press), §8.6 and Chapter 12 (SVD). QR decomposition is discussed in §5.2.6.[3]

Lawson, C.L., and Hanson, R. 1974, Solving Least Squares Problems (Englewood Cliffs, NJ: Prentice-Hall); reprinted 1995 (Philadelphia: S.I.A.M.), Chapter 18.

Wilkinson, J.H., and Reinsch, C. 1971, Linear Algebra, vol. II of Handbook for Automatic Computation (New York: Springer), Chapter I.10 by G.H. Golub and C. Reinsch.[4]

Anderson, E., et al. 1999, LAPACK User's Guide, 3rd ed. (Philadelphia: S.I.A.M.). Online with software at 2007+, http://www.netlib.org/lapack.[5]

Smith, B.T., et al. 1976, Matrix Eigensystem Routines — EISPACK Guide, 2nd ed., vol. 6 of Lecture Notes in Computer Science (New York: Springer).

Stoer, J., and Bulirsch, R. 2002, Introduction to Numerical Analysis, 3rd ed. (New York: Springer), §6.7.[6]

2.7 稀疏线性方程组

如果一个线性方程组的矩阵中仅有相对较少的元素 $a_{ij}$ 非零，则称该方程组为稀疏的。对这类问题使用通用的线性代数方法是浪费的，因为求解方程组或矩阵求逆所需的 $O(N^3)$ 次算术运算中，大部分涉及的是零操作数。此外，你可能希望处理规模大到接近内存极限的问题，而为无用的零元素预留存储空间也是浪费的。需要注意的是，任何稀疏矩阵方法通常有两个不同的（且并不总是一致的）目标：节省时间 和/或 节省空间。

我们在§2.4中讨论过一种典型的稀疏形式：带状对角矩阵。例如，在三对角情形下，我们看到可以同时节省时间（从 $N^3$ 降至 $N$ 阶）和空间（从 $N^2$ 降至 $N$ 阶）。其求解方法在原理上与通用的 $LU$ 分解方法并无不同，只是巧妙地应用了该方法，并仔细处理了零元素的记录问题。许多处理稀疏问题的实用方案也具有这种特性：它们本质上是分解方案，或者是类似于高斯-约当消元法的消去方案，但经过精心优化，以尽量减少所谓的

填充元（fill-ins）——即在求解过程中原本为零但必须变为非零的元素，这些元素需要预留存储空间。

因此，直接求解稀疏方程组的方法严重依赖于矩阵稀疏模式的具体结构。那些频繁出现的稀疏模式，或在化简更一般形式过程中有用的中间模式，已有专门的名称和对应的求解方法。此处无法详细综述这些内容。本节末尾列出的参考文献可为你提供进入专门文献的入口，而以下术语列表（以及图2.7.1）至少能让你在鸡尾酒会上应对自如：

• 三对角（tridiagonal）
• 带宽为 $M$ 的带状对角（或带状）（band-diagonal (or banded) with bandwidth $M$）
• 带状三角（band triangular）
• 块对角（block diagonal）
• 块三对角（block tridiagonal）
• 块三角（block triangular）
• 循环带状（cyclic banded）
• 单（或双）边界块对角（singly (or doubly) bordered block diagonal）
• 单（或双）边界块三角（singly (or doubly) bordered block triangular）
• 单（或双）边界带状对角（singly (or doubly) bordered band-diagonal）
• 单（或双）边界带状三角（singly (or doubly) bordered band triangular）
• 其他（!）

你还应了解在二维或更高维偏微分方程求解中出现的一些特殊稀疏形式。参见第20章。

如果你的稀疏模式并不简单，那么你可能希望尝试一种“分析/分解/运算”（analyze/factorize/operate）软件包，它能自动确定如何最小化填充元。分析阶段对每种稀疏模式只需执行一次；分解阶段对符合该模式的每个具体矩阵执行一次；运算阶段则对每个与该矩阵配合使用的右端项执行一次。有关这方面的参考文献，见[2,3]。NAG库[4]具备分析/分解/运算功能。IMSL[5]也提供了大量稀疏矩阵计算例程，即耶鲁稀疏矩阵包（Yale Sparse Matrix Package）[6]。

你应当意识到，稀疏矩阵方法为最小化填充元和算术运算而规定的特殊交换与消元顺序，通常会降低方法的数值稳定性（与例如带主元选取的常规 $LU$ 分解相比）。若可能，将问题进行缩放，使非零矩阵元素具有相近的量级，有时可缓解这一问题。

在本节的其余部分，我们将介绍一些适用于某些一般稀疏矩阵类别的概念，这些概念并不一定依赖于稀疏模式的具体细节。

2.7.1 Sherman-Morrison 公式

假设你已经通过艰苦卓绝的努力得到了一个方阵 $\mathbf{A}$ 的逆矩阵 ${\mathbf{A}}^{-1}$。现在你想对 $\mathbf{A}$ 做一个“小”的修改，例如改变一个元素 $a_{ii}$、几个元素、一行或一列。有没有什么办法可以在不重复你艰苦工作的情况下，计算出 ${\mathbf{A}}^{-1}$ 相应的变化？答案是肯定的，前提是你的修改具有如下形式：

$$\mathbf{A}\to (\mathbf{A}+\mathbf{u}\otimes \mathbf{v})$$

其中 $\mathbf{u}$ 和 $\mathbf{v}$ 是某些向量。（回忆一下，$\mathbf{u}\otimes \mathbf{v}$ 是一个矩阵，其第 $i,j$ 个元素是 $\mathbf{u}$ 的第 $i$ 个分量与 $\mathbf{v}$ 的第 $j$ 个分量的乘积。）如果 $\mathbf{u}$ 是单位向量 ${\mathbf{e}}_i$，那么 (2.7.1) 将 $\mathbf{v}$ 的分量加到第 $i$ 行；如果 $\mathbf{v}$ 是单位向量 ${\mathbf{e}}_j$，那么 (2.7.1) 将 $\mathbf{u}$ 的分量加到第 $j$ 列；如果 $\mathbf{u}$ 和 $\mathbf{v}$ 分别与单位向量 ${\mathbf{e}}_i$ 和 ${\mathbf{e}}_j$ 成比例，则仅在元素 $a_{ij}$ 上增加一项。

Sherman-Morrison 公式给出了 $(\mathbf{A}+\mathbf{u}\otimes \mathbf{v}{)}^{-1}$，其简要推导如下：

$$\begin{array}{rl}& (\mathbf{A}+\mathbf{u}\otimes \mathbf{v}{)}^{-1}=(1+{\mathbf{A}}^{-1}\cdot \mathbf{u}\otimes \mathbf{v}{)}^{-1}\cdot {\mathbf{A}}^{-1}\\ & =(1-{\mathbf{A}}^{-1}\cdot \mathbf{u}\otimes \mathbf{v}+{\mathbf{A}}^{-1}\cdot \mathbf{u}\otimes \mathbf{v}\cdot {\mathbf{A}}^{-1}\cdot \mathbf{u}\otimes \mathbf{v}-\dots )\cdot {\mathbf{A}}^{-1}\\ & ={\mathbf{A}}^{-1}-{\mathbf{A}}^{-1}\cdot \mathbf{u}\otimes \mathbf{v}\cdot {\mathbf{A}}^{-1}\left(1-\lambda +{\lambda }^2-\dots \right)\\ & ={\mathbf{A}}^{-1}-\frac{({\mathbf{A}}^{-1}\cdot \mathbf{u})\otimes (\mathbf{v}\cdot {\mathbf{A}}^{-1})}{1+\lambda }\end{array}\text{\hspace{1em}(2.7)}$$

其中

$$\lambda \equiv \mathbf{v}\cdot {\mathbf{A}}^{-1}\cdot \mathbf{u}$$

(2.7.2) 的第二行是一个形式上的幂级数展开。第三行利用了外积和内积的结合律，将标量 $\lambda$ 提取出来。

(2.7.2) 的使用方法如下：给定 ${\mathbf{A}}^{-1}$ 以及向量 $\mathbf{u}$ 和 $\mathbf{v}$，我们只需进行两次矩阵乘法和一次向量点积：

$$\mathbf{z}\equiv {\mathbf{A}}^{-1}\cdot \mathbf{u}\mathbf{w}\equiv ({\mathbf{A}}^{-1}{)}^T\cdot \mathbf{v}\lambda =\mathbf{v}\cdot \mathbf{z}$$

即可得到逆矩阵的所需变化：

$${\mathbf{A}}^{-1}\to {\mathbf{A}}^{-1}-\frac{\mathbf{z}\otimes \mathbf{w}}{1+\lambda }$$

整个过程仅需 $3N^2$ 次乘法和大致相同数量的加法（如果 $\mathbf{u}$ 或 $\mathbf{v}$ 是单位向量，则计算量更少）。

Sherman-Morrison 公式可以直接应用于一类稀疏问题。如果你已经有一种快速计算 ${\mathbf{A}}^{-1}$ 的方法（例如三对角矩阵或其他标准稀疏形式），那么通过 (2.7.4)–(2.7.5) 可以逐步构建出相关但更复杂的形式，例如逐行或逐列地添加修正项。注意，你可以多次连续应用 Sherman-Morrison 公式，在每一步都使用最新更新的 ${\mathbf{A}}^{-1}$（见公式 2.7.5）。当然，如果你需要修改每一行，那么你又回到了 $N^3$ 的方法。此时 $N^3$ 前面的常数仅比更好的直接方法差几倍，但你失去了选主元带来的数值稳定性优势——因此要谨慎使用。

对于另一些稀疏问题，Sherman-Morrison 公式无法直接应用，原因很简单：存储整个逆矩阵 ${\mathbf{A}}^{-1}$ 是不可行的。如果你只想添加一个形如 $\mathbf{u}\otimes \mathbf{v}$ 的修正项，并求解线性系统

$$(\mathbf{A}+\mathbf{u}\otimes \mathbf{v})\cdot \mathbf{x}=\mathbf{b}$$

那么你可以按如下方式进行。利用假定已有的针对矩阵 $\mathbf{A}$ 的快速方法，求解两个辅助问题：

$$\mathbf{A}\cdot \mathbf{y}=\mathbf{b}\mathbf{A}\cdot \mathbf{z}=\mathbf{u}$$

得到向量 $\mathbf{y}$ 和 $\mathbf{z}$。于是解为

$$\mathbf{x}=\mathbf{y}-\left[\frac{\mathbf{v}\cdot \mathbf{y}}{1+(\mathbf{v}\cdot \mathbf{z})}\right]\mathbf{z}$$

这一点可以通过将 (2.7.2) 右乘 $\mathbf{b}$ 得到。

2.7.2 循环三对角系统

所谓的循环三对角系统经常出现，是上述 Sherman-Morrison 公式应用方式的一个良好示例。这类方程组具有如下形式：

$$\left[\begin{array}{lllll}{b}_0& c_0& 0& \cdots & \beta \\ a_1& b_1& c_1& \cdots & 0\\ 0& a_2& b_2& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ \alpha & 0& \cdots & a_{N-1}& b_{N-1}\end{array}\right]\cdot \left[\begin{array}{l}{x}_0\\ x_1\\ x_2\\ ⋮\\ x_{N-1}\end{array}\right]=\left[\begin{array}{l}{r}_0\\ r_1\\ r_2\\ ⋮\\ r_{N-1}\end{array}\right]$$

这是一个三对角系统，只是在矩阵的角落多了元素 $\alpha$ 和 $\beta$。这种形式通常由具有周期性边界条件的微分方程的有限差分离散化产生（见 §20.4）。

我们使用 Sherman-Morrison 公式，将该系统视为三对角矩阵加上一个修正项。按照方程 (2.7.6) 的记号，定义向量 $\mathbf{u}$ 和 $\mathbf{v}$ 为

$$\mathbf{u}=\left[\begin{array}{l}\gamma \\ 0\\ ⋮\\ 0\\ \alpha \end{array}\right]\mathbf{v}=\left[\begin{array}{l}1\\ 0\\ ⋮\\ 0\\ \beta /\gamma \end{array}\right]$$

此处 $\gamma$ 暂时是任意的。于是矩阵 $\mathbf{A}$ 是 (2.7.9) 式中矩阵的三对角部分，但其中两项被修改为：

$$b_0^{\prime }=b_0-\gamma ,b_{N-1}^{\prime }=b_{N-1}-\alpha \beta /\gamma$$

我们现在用标准的三对角算法求解方程 (2.7.7)，然后通过方程 (2.7.8) 得到解。

下面的 cyclic 例程实现了该算法。我们选择任意参数 $\gamma =-b_0$，以避免在 (2.7.11) 式的第一个方程中因相减而损失精度。如果这种选择（不太可能）导致第二个方程出现精度损失，你可以另选其他值。

void cyclic(VecDoub_I &a, VecDoub_I &b, VecDoub_I &c, const Doub alpha, const Doub beta, VecDoub_I &r, VecDoub_O &x)

求解由 (2.7.9) 式给出的“循环”线性方程组，得到向量 $x[\mathrm{0..}n-1]$。输入向量 $a$、$b$、$c$ 和 $r$ 的维数均为 $[\mathrm{0..}n-1]$，而 $\alpha$ 和 $\beta$ 是矩阵的两个角点元素。输入数据不会被修改。

{
    Int i, n = a.size();
    Doub fact, gamma;
    if (n <= 2) throw("n too small in cyclic");
}

VecDoub bb(n), u(n), z(n);
gamma = -b[0];
bb[0] = b[0] - gamma;
bb[n-1] = b[n-1] - alpha * beta / gamma;
for (i = 1; i < n - 1; i++) bb[i] = b[i];
tridag(a, bb, c, r, x);
u[0] = gamma;
u[n-1] = alpha;
for (i = 1; i < n - 1; i++) u[i] = 0.0;
tridag(a, bb, c, u, z);
fact = (x[0] + beta * x[n-1] / gamma) / (1.0 + z[0] + beta * z[n-1] / gamma);
for (i = 0; i < n; i++) x[i] -= fact * z[i]; // Now get the solution vector x.

2.7.3 Woodbury 公式

如果你想添加不止一个修正项，就不能重复使用 (2.7.8) 式，因为在第一步之后，若不存储新的 ${\mathbf{A}}^{-1}$，你将无法高效地求解辅助问题 (2.7.7)。此时你需要 Woodbury 公式，它是 Sherman-Morrison 公式的分块矩阵版本：

$$\begin{array}{rl}& (\mathbf{A}+\mathbf{U}\cdot {\mathbf{V}}^T{)}^{-1}\\ & ={\mathbf{A}}^{-1}-\left[{\mathbf{A}}^{-1}\cdot \mathbf{U}\cdot (\mathbf{I}+{\mathbf{V}}^T\cdot {\mathbf{A}}^{-1}\cdot \mathbf{U}{)}^{-1}\cdot {\mathbf{V}}^T\cdot {\mathbf{A}}^{-1}\right]\end{array}$$

这里 $\mathbf{A}$ 仍是 $N\times N$ 矩阵，而 $\mathbf{U}$ 和 $\mathbf{V}$ 是 $N\times P$ 矩阵，其中 $P<N$，通常 $P\ll N$。若将修正项的内部部分写成如下形式，其结构会更清晰：

$$\left[\begin{array}{c}\mathbf{U}\\ \nabla \end{array}\right]\cdot {\left[\mathbf{I}+{\mathbf{V}}^T\cdot {\mathbf{A}}^{-1}\cdot \mathbf{U}\right]}^{-1}\cdot \left[\begin{array}{c}\nabla \\ \nabla \end{array}\right]$$

从中可以看出，需要求逆的矩阵仅为 $P\times P$，而非 $N\times N$。

Woodbury 公式与 Sherman-Morrison 公式多次应用之间的关系可通过以下观察得以澄清：若 $\mathbf{U}$ 是由 $P$ 个向量 ${\mathbf{u}}_0,\dots ,{\mathbf{u}}_{P-1}$ 作为列构成的矩阵，$\mathbf{V}$ 是由 $P$ 个向量 ${\mathbf{v}}_0,\dots ,{\mathbf{v}}_{P-1}$ 作为列构成的矩阵，

$$\mathbf{U}\equiv \left[\begin{array}{l}{\mathbf{u}}_0\\ ⋮\end{array}\right]\cdots \left[\begin{array}{l}{\mathbf{u}}_{P-1}\\ ⋮\end{array}\right]\mathbf{V}\equiv \left[\begin{array}{l}{\mathbf{v}}_0\\ ⋮\end{array}\right]\cdots \left[\begin{array}{l}{\mathbf{v}}_{P-1}\\ ⋮\end{array}\right]$$

则对 $\mathbf{A}$ 的同一修正有两种等价表达方式：

$$\left(\mathbf{A}+\sum _{k=0}^{P-1}{\mathbf{u}}_k\otimes {\mathbf{v}}_k\right)=(\mathbf{A}+\mathbf{U}\cdot {\mathbf{V}}^T)$$

（注意：$\mathbf{u}$ 和 $\mathbf{v}$ 的下标并非表示分量，而是用于区分不同的列向量。）

方程 (2.7.15) 表明，如果你已将 ${\mathbf{A}}^{-1}$ 存储在内存中，那么你可以选择以下两种方式之一进行 $P$ 次修正：要么利用 (2.7.12) 式一次性完成，并对一个 $P\times P$ 矩阵求逆；要么连续 $P$ 次应用 (2.7.5) 式。

如果你没有足够的存储空间保存 ${\mathbf{A}}^{-1}$，则必须按如下方式使用 (2.7.12) 式：为求解线性方程

$$\left(\mathbf{A}+\sum _{k=0}^{P-1}{\mathbf{u}}_k\otimes {\mathbf{v}}_k\right)\cdot \mathbf{x}=\mathbf{b}$$

首先求解 $P$ 个辅助问题：

$$\begin{array}{rl}& \mathbf{A}\cdot {\mathbf{z}}_0={\mathbf{u}}_0\\ & \mathbf{A}\cdot {\mathbf{z}}_1={\mathbf{u}}_1\\ & \cdots \end{array}$$

$$\mathbf{A}\cdot {\mathbf{z}}_{P-1}={\mathbf{u}}_{P-1}$$

并用所得到的 $\mathbf{z}$ 向量按列构造矩阵 $\mathbf{Z}$：

$$\mathbf{Z}\equiv \left[\begin{array}{l}{\mathbf{z}}_0\\ ⋮\\ {\mathbf{z}}_{P-1}\end{array}\right]$$

接下来，进行 $P\times P$ 矩阵求逆：

$$\mathbf{H}\equiv (\mathbf{I}+{\mathbf{V}}^T\cdot \mathbf{Z}{)}^{-1}$$

最后，再求解一个辅助问题：

$$\mathbf{A}\cdot \mathbf{y}=\mathbf{b}$$

用上述这些量表示，解为：

$$\mathbf{x}=\mathbf{y}-\mathbf{Z}\cdot \left[\mathbf{H}\cdot ({\mathbf{V}}^T\cdot \mathbf{y})\right]$$

2.7.4 分块求逆

偶尔你会遇到一个矩阵（甚至不一定稀疏），可以通过分块方法高效地求逆。假设 $N\times N$ 的矩阵 $\mathbf{A}$ 被分块为：

$$\mathbf{A}=\left[\begin{array}{ll}\mathbf{P}& \mathbf{Q}\\ \mathbf{R}& \mathbf{S}\end{array}\right]$$

其中 $\mathbf{P}$ 和 $\mathbf{S}$ 分别是 $p\times p$ 和 $s\times s$ 的方阵（$p+s=N$）。矩阵 $\mathbf{Q}$ 和 $\mathbf{R}$ 不一定是方阵，其大小分别为 $p\times s$ 和 $s\times p$。

若 $\mathbf{A}$ 的逆矩阵也按相同方式分块：

$${\mathbf{A}}^{-1}=\left[\begin{array}{ll}\mathbf{P}& \mathbf{Q}\\ \mathbf{R}& \mathbf{S}\end{array}\right]$$

则 $\tilde{\mathbf{P}}$、$\tilde{\mathbf{Q}}$、$\tilde{\mathbf{R}}$、$\tilde{\mathbf{S}}$（其大小分别与 $\mathbf{P}$、$\mathbf{Q}$、$\mathbf{R}$、$\mathbf{S}$ 相同）可通过以下公式之一求得：

$$\begin{array}{rl}& \mathbf{P}=(\mathbf{P}-\mathbf{Q}\cdot {\mathbf{S}}^{-1}\cdot \mathbf{R}{)}^{-1}\\ & \mathbf{Q}=-(\mathbf{P}-\mathbf{Q}\cdot {\mathbf{S}}^{-1}\cdot \mathbf{R}{)}^{-1}\cdot (\mathbf{Q}\cdot {\mathbf{S}}^{-1})\\ & \mathbf{R}=-({\mathbf{S}}^{-1}\cdot \mathbf{R})\cdot (\mathbf{P}-\mathbf{Q}\cdot {\mathbf{S}}^{-1}\cdot \mathbf{R}{)}^{-1}\\ & \mathbf{S}={\mathbf{S}}^{-1}+({\mathbf{S}}^{-1}\cdot \mathbf{R})\cdot (\mathbf{P}-\mathbf{Q}\cdot {\mathbf{S}}^{-1}\cdot \mathbf{R}{)}^{-1}\cdot (\mathbf{Q}\cdot {\mathbf{S}}^{-1})\end{array}$$

或者通过以下等价公式：

$$\begin{array}{rl}& \mathbf{P}={\mathbf{P}}^{-1}+({\mathbf{P}}^{-1}\cdot \mathbf{Q})\cdot (\mathbf{S}-\mathbf{R}\cdot {\mathbf{P}}^{-1}\cdot \mathbf{Q}{)}^{-1}\cdot (\mathbf{R}\cdot {\mathbf{P}}^{-1})\\ & \mathbf{Q}=-({\mathbf{P}}^{-1}\cdot \mathbf{Q})\cdot (\mathbf{S}-\mathbf{R}\cdot {\mathbf{P}}^{-1}\cdot \mathbf{Q}{)}^{-1}\\ & \mathbf{R}=-(\mathbf{S}-\mathbf{R}\cdot {\mathbf{P}}^{-1}\cdot \mathbf{Q}{)}^{-1}\cdot (\mathbf{R}\cdot {\mathbf{P}}^{-1})\\ & \mathbf{S}=(\mathbf{S}-\mathbf{R}\cdot {\mathbf{P}}^{-1}\cdot \mathbf{Q}{)}^{-1}\end{array}$$

公式 (2.7.24) 和 (2.7.25) 中的括号突出了可能只需计算一次的重复因子。（当然，根据结合律，你可以按任意顺序进行矩阵乘法。）选择使用公式 (2.7.24) 还是 (2.7.25)，取决于你希望 $\tilde{\mathbf{P}}$ 或 $\tilde{\mathbf{S}}$ 具有更简单的表达式；或者取决于重复表达式 $(\mathbf{S}-\mathbf{R}\cdot {\mathbf{P}}^{-1}\cdot \mathbf{Q}{)}^{-1}$ 是否比 $(\mathbf{P}-\mathbf{Q}\cdot {\mathbf{S}}^{-1}\cdot \mathbf{R}{)}^{-1}$ 更容易计算；或者取决于 $\mathbf{P}$ 和 $\mathbf{S}$ 的相对大小；或者取决于 ${\mathbf{P}}^{-1}$ 或 ${\mathbf{S}}^{-1}$ 是否已经已知。

另一个有时有用的公式是分块矩阵的行列式：

$$\det \mathbf{A}=\det \mathbf{P}\det (\mathbf{S}-\mathbf{R}\cdot {\mathbf{P}}^{-1}\cdot \mathbf{Q})=\det \mathbf{S}\det (\mathbf{P}-\mathbf{Q}\cdot {\mathbf{S}}^{-1}\cdot \mathbf{R})$$

2.7.5 稀疏矩阵的索引存储

我们已经看到（§2.4），三对角或带状矩阵可以采用一种紧凑格式存储，仅分配非零元素所需的空间，可能还会额外分配少量空间以简化管理。那么更一般的稀疏矩阵呢？当一个 $M\times N$ 的稀疏矩阵仅包含若干倍于 $M$ 或 $N$ 的非零元素（这是典型情况）时，为所有 $MN$ 个元素分配存储空间显然是低效的——甚至常常在物理上不可行。即使分配了这样的存储空间，在所有元素中循环搜索非零元素也会在机器时间上造成低效甚至不可接受的开销。

显然，需要某种索引存储方案，该方案仅存储非零矩阵元素，并附带足够的辅助信息，以确定每个元素的逻辑位置，以及在常见矩阵运算中如何遍历这些元素。不幸的是，目前并没有一种被普遍采用的标准方案。每种方案都有其优缺点，具体取决于应用场景。

在讨论稀疏矩阵之前，先考虑更简单的稀疏向量问题。显然的数据结构是：一个非零值列表和另一个对应位置的列表：

行数。
非零元素的最大数量。

VecInt row_ind;
VecDoub val;
NRsparseCol(Int m, Int nnvals) : nrows(m), nvals(nnvals),
    row_ind(nnvals, 0), val(nnvals, 0.0) {}
// 构造函数。将向量初始化为零。

NRsparseCol() : nrows(0), nvals(0), row_ind(), val() {}
// 默认构造函数。

void resize(Int m, Int nnvals) {
    nrows = m;
    nvals = nnvals;
    row_ind.assign(nnvals, 0);
    val.assign(nnvals, 0.0);
}

虽然我们将其视为定义一个列向量，但你也可以完全使用相同的数据结构表示行向量——只需在概念上交换变量中行和列的含义即可。然而对于矩阵，我们必须事先决定使用行导向还是列导向的存储方式。

一种简单的方案是使用稀疏列的向量：

NRvector<NRsparseCol*> a;
for (i = 0; i < n; i++) {
    nvals = ...;
    a[i] = new NRsparseCol(m, nvals);
}

每一列通过如下语句填充：

count = 0;
for (j = ...) {
    a[i]->row_ind[count] = ...;
    a[i]->val[count] = ...;
    count++;
}

该数据结构适用于主要处理矩阵列的算法，但当需要遍历矩阵所有元素时效率不高。

一种良好的通用存储方案是压缩列存储格式（compressed column storage format）。该格式有时也称为 Harwell-Boeing 格式，得名于最早系统性地为研究目的提供标准稀疏矩阵集合的两个大型机构。在此方案中，使用三个向量：val 存储按列优先顺序遍历得到的非零值，row_ind 存储每个非零值对应的行索引，colptr 存储每列在前两个数组中的起始位置。换句话说，若 val[k] = a[i][j]，则 row_ind[k] = i。第 j 列的第一个非零元素位于 colptr[j]，最后一个位于 colptr[j+1] - 1。注意 colptr[0] 始终为 0，且按惯例定义 colptr[n] 等于非零元素总数。还需注意 colptr 数组的维度是 $N+1$，而非 $N$。该方案的优点是仅需约两倍于非零矩阵元素数量的存储空间。（其他方法可能需要三倍甚至五倍的存储空间。）

例如，考虑如下矩阵：

$$\left[\begin{array}{lllll}3.0& 0.0& 1.0& 2.0& 0.0\\ 0.0& 4.0& 0.0& 0.0& 0.0\\ 0.0& 7.0& 5.0& 9.0& 0.0\\ 0.0& 0.0& 0.0& 0.0& 0.0\\ 0.0& 0.0& 0.0& 6.0& 5.0\end{array}\right]$$

在压缩列存储模式下，矩阵 (2.7.27) 由两个长度为 9 的数组和一个长度为 6 的数组表示，如下所示：

index k	0	1	2	3	4	5	6	7	8
val[k]	3.0	4.0	7.0	1.0	5.0	2.0	9.0	6.0	5.0
row_ind[k]	0	1	2	0	2	0	2	4	4

index i	0	1	2	3	4	5
colptr[i]	0	1	3	5	8	9

注意，根据存储规则，$N$（即 5）是 colptr 中有效的最大索引。colptr[5] 的值为 9，即另外两个数组的长度。例如，第 2 列中的元素 1.0 和 5.0 位于位置 colptr[2] $\le k<\text{colptr}[3]$。

以下是用于处理此存储方案的数据结构：

NRsparseMat();
NRsparseMat(Int m, Int n, Int nnvals);
VecDoub ax(const VecDoub &x) const;
VecDoub atx(const VecDoub &x) const;
NRsparseMat transpose() const;

• 默认构造函数。
• 构造函数。将向量初始化为零。
• 计算 $\mathbf{A}$ 与向量 x[0..ncols-1] 的乘积。
• 计算 ${\mathbf{A}}^T$ 与向量 x[0..nrows-1] 的乘积。
• 构造 ${\mathbf{A}}^T$。

构造函数的代码是标准的：

NRsparseMat::NRsparseMat() : nrows(0), ncols(0), nvals(0), colptr(), row_ind(), val() {}
NRsparseMat::NRsparseMat(Int m, Int n, Int nnvals) : nrows(m), ncols(n), nvals(nnvals), colptr(n+1, 0), row_ind(nnvals, 0), val(nnvals, 0.0) {}

在压缩列存储模式下，矩阵最重要的用途是右乘一个向量。不要通过遍历 $\mathbf{A}$ 的行来实现此操作，因为在此存储模式下效率极低。正确的方法如下：

VecDoub NRsparseMat::ax(const VecDoub &x) const {
    VecDoub y(nrows, 0.0);
    for (Int j = 0; j < ncols; j++) {
        for (Int i = colptr[j]; i < colptr[j+1]; i++) {
            y[row_ind[i]] += val[i] * x[j];
        }
    }
    return y;
}

由于间接寻址，会存在一些效率损失。尽管存在其他能最小化此问题的存储模式，但它们也有自身的缺点。

右乘矩阵转置与向量也很简单，因为我们直接遍历列即可。（仍需间接寻址。）注意，这里并未实际构造转置矩阵。

VecDoub NRsparseMat::atx(const VecDoub &x) const {
    VecDoub y(ncols, 0.0);
    for (Int i = 0; i < ncols; i++) {
        for (Int j = colptr[i]; j < colptr[i+1]; j++) {
            y[i] += val[j] * x[row_ind[j]];
        }
    }
    return y;
}

由于压缩列存储对行和列的处理方式差异很大，若给定一个以压缩列存储的矩阵，构造其转置矩阵是一个相当复杂的过程。当无法避免此操作时，可采用如下方法：

NRsparseMat NRsparseMat::transpose() const {
    Int i, j, k, index, m = nrows, n = ncols;
    NRsparseMat at(n, m, nvals); // initialized to zero.
    // First find the column lengths for A^T, i.e., the row lengths of A.
    VecInt count(m, 0); // Temporary counters for each row of A.
    for (i = 0; i < n; i++) {
        for (j = colptr[i]; j < colptr[i+1]; j++) {
            k = row_ind[j];
            count[k]++;
        }
    }
    // Now set at.colptr. 0th entry stays 0.
    for (j = 0; j < m; j++) {
        at.colptr[j+1] = at.colptr[j] + count[j];
    }
    for (j = 0; j < m; j++) {
        count[j] = 0;
    }
    // Main loop.
    for (i = 0; i < n; i++) {
        for (j = colptr[i]; j < colptr[i+1]; j++) {
            k = row_ind[j];
            index = at.colptr[k] + count[k];
            at.row_ind[index] = i;
            at.val[index] = val[j];
            count[k]++;
        }
    }
    return at;
}

我们仅提供一种稀疏矩阵-矩阵乘法例程，用于计算乘积 ${\mathbf{ADA}}^T$，其中 $\mathbf{D}$ 是对角矩阵。该乘积用于线性规划内点法中构造所谓的正规方程（$\S$10.11）。我们将该算法封装在独立的结构 ADAT 中：

算法分为两步。首先，通过调用构造函数确定 $\mathbf{A}{\mathbf{A}}^T$ 的非零模式。由于 $\mathbf{D}$ 是对角矩阵，${\mathbf{ADA}}^T$ 与 $\mathbf{A}{\mathbf{A}}^T$ 具有相同的非零结构。使用 ADAT 的算法通常同时拥有 $\mathbf{A}$ 和 ${\mathbf{A}}^T$，因此我们将两者都传递给构造函数，而不是从 $\mathbf{A}$ 重新计算 ${\mathbf{A}}^T$。构造函数分配存储空间，并为 colptr 和 row_ind 赋值。ADAT 的结构以列排序的形式返回，因为 $\S$10.11 中使用的 AMD 排序等例程需要此格式。

ADAT::ADAT(const NRsparseMat &A, const NRsparseMat &AT) : a(A), at(AT) {
    Int i, j, k, l, nvals, m = AT.ncols;
    VecInt done(m);
    // First pass: Count nonzeros.
    for (i = 0; i < m; i++) {
        done[i] = -1;
    }
    nvals = 0;
    for (j = 0; j < m; j++) {
        for (i = at.colptr[j]; i < at.colptr[j+1]; i++) {
            k = at.row_ind[i];
            for (l = a.colptr[k]; l < a.colptr[k+1]; l++) {
                h = a.row_ind[l];
                if (done[h] != j) {
                    done[h] = j;
                    nvals++;
                }
            }
        }
    }

    adat = new NRsparseMat(m, m, nvals);
    // Second pass: Determine columns of adat.
    for (i = 0; i < m; i++) {
        done[i] = -1;
    }
    nvals = 0;
    for (j = 0; j < m; j++) {
        adat->colptr[j] = nvals;
        for (i = at.colptr[j]; i < at.colptr[j+1]; i++) {
            k = at.row_ind[i];
            for (l = a.colptr[k]; l < a.colptr[k+1]; l++) {
                h = a.row_ind[l];
                if (done[h] != j) {
                    done[h] = j;
                    adat->row_ind[nvals] = h;
                    nvals++;
                }
            }
        }
    }
    adat->colptr[m] = nvals;

    // Sort each column.
    for (j = 0; j < m; j++) {
        Int i_start = adat->colptr[j];
        Int size = adat->colptr[j+1] - i_start;
        if (size > 1) {
            VecInt col(size, &adat->row_ind[i_start]);
            sort(col);
            for (k = 0; k < size; k++) {
                adat->row_ind[i_start + k] = col[k];
            }
        }
    }
}

下一个例程 updateD 实际填充 val 数组中的值。对于固定的 $\mathbf{A}$，可重复调用此例程以更新 ${\mathbf{ADA}}^T$。

void ADAT::updateD(const VecDoub &D) {
    Int i, j, k, l, m = a.nrows, n = a.ncols;
    VecDoub temp(n), temp2(m, 0.0);
    for (i = 0; i < m; i++) {
        // Compute temp = D * A^T(:, i)
        for (j = at.colptr[i]; j < at.colptr[i+1]; j++) {
            k = at.row_ind[j];
            temp[k] = at.val[j] * D[k];
        }
        // Compute temp2 = A * temp
        for (j = at.colptr[i]; j < at.colptr[i+1]; j++) {
            k = at.row_ind[j];
            for (l = a.colptr[k]; l < a.colptr[k+1]; l++) {
                h = a.row_ind[l];
                temp2[h] += temp[k] * a.val[l];
            }
        }
        // Store temp2 in column i of adat
        for (j = adat->colptr[i]; j < adat->colptr[i+1]; j++) {
            k = adat->row_ind[j];
            adat->val[j] = temp2[k];
            temp2[k] = 0.0;
        }
    }
}

最后两个函数很简单。ref 例程返回对结构中存储的矩阵 ${\mathbf{ADA}}^T$ 的引用，供其他可能需要处理该矩阵的例程使用。析构函数则释放存储空间。

NRsparseMat & ADAT::ref() {
    return *adat;
}

ADAT::~ADAT() { delete adat; }

顺便提一下，如果你用不同的矩阵 $\mathbf{A}$ 和 ${\mathbf{B}}^T$ 调用 ADAT，只要 $\mathbf{A}$ 和 $\mathbf{B}$ 具有相同的非零元模式，一切都会正常工作。

在《Numerical Recipes》第二版中，我们介绍了一种相关的稀疏矩阵存储方式：先存储矩阵的对角线元素，再存储非对角线元素。我们现在认为，对于本书中的任何用途而言，这种方案增加的复杂性并不值得。关于这种及其他存储方案的讨论，参见 [7,8]。若想了解如何在压缩列存储格式下处理对角线元素，请参看本节末尾的 asolve 函数代码。

2.7.6 稀疏系统的共轭梯度法

所谓的共轭梯度法为求解 $N\times N$ 线性方程组

$$\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$$

提供了一种相当通用的手段。

对于大型稀疏系统而言，这些方法的吸引力在于：它们仅通过矩阵 $\mathbf{A}$ 与向量的乘法（或其转置与向量的乘法）来引用 $\mathbf{A}$。正如我们所见，对于适当存储的稀疏矩阵，这些运算可以非常高效。作为矩阵 $\mathbf{A}$ 的“所有者”，你可以提供尽可能高效的稀疏矩阵乘法函数。而我们这些“宏观策略制定者”则提供一个抽象基类 Linbcg（见下文），其中包含了利用你提供的函数来求解线性方程组 (2.7.29) 的方法。

最简单的“普通”共轭梯度算法 [9–11] 仅在 $\mathbf{A}$ 对称且正定时才能求解 (2.7.29)。该算法基于最小化如下函数的思想：

$$\begin{array}{r}f(\mathbf{x})=\frac{1}{2}\mathbf{x}\cdot \mathbf{A}\cdot \mathbf{x}-\mathbf{b}\cdot \mathbf{x}\end{array}$$

当该函数的梯度

$$\nabla f=\mathbf{A}\cdot \mathbf{x}-\mathbf{b}$$

为零时，函数取得最小值，这等价于方程 (2.7.29)。最小化过程通过生成一系列搜索方向 ${\mathbf{p}}_k$ 和改进的极小值点 ${\mathbf{x}}_k$ 来实现。在每一步中，找到一个标量 ${\alpha }_k$ 使得 $f({\mathbf{x}}_k+{\alpha }_k{\mathbf{p}}_k)$ 最小，并将 ${\mathbf{x}}_{k+1}$ 设为新点 ${\mathbf{x}}_k+{\alpha }_k{\mathbf{p}}_k$。${\mathbf{p}}_k$ 和 ${\mathbf{x}}_k$ 的构造方式保证了 ${\mathbf{x}}_{k+1}$ 同时也是函数 $f$ 在已取方向所张成的整个向量空间 $\{{\mathbf{p}}_0,{\mathbf{p}}_1,\cdots ,{\mathbf{p}}_{k-1}\}$ 上的极小值点。经过 $N$ 次迭代后，即可得到整个向量空间上的极小值点，即方程 (2.7.29) 的解。

稍后在 §10.8 中，我们将把这种“普通”共轭梯度算法推广到任意非线性函数的最小化问题。而在这里，我们的兴趣在于求解线性方程组（不一定正定或对称），此时另一种推广更为重要，即双共轭梯度法（biconjugate gradient method）。该方法通常与函数最小化没有简单的联系。它构造了四组向量序列：${\mathbf{r}}_k$、${\overline{\mathbf{r}}}_k$、${\mathbf{p}}_k$、${\overline{\mathbf{p}}}_k$（$k=0,1,\dots$）。你提供初始向量 ${\mathbf{r}}_0$ 和 ${\overline{\mathbf{r}}}_0$，并设 ${\mathbf{p}}_0={\mathbf{r}}_0$、${\overline{\mathbf{p}}}_0={\overline{\mathbf{r}}}_0$。然后执行以下递推关系：

$$\begin{array}{r}{\alpha }_k=\frac{{\overline{\mathbf{r}}}_k\cdot {\mathbf{r}}_k}{{\overline{\mathbf{p}}}_k\cdot \mathbf{A}\cdot {\mathbf{p}}_k}\\ {\mathbf{r}}_{k+1}={\mathbf{r}}_k-{\alpha }_k\mathbf{A}\cdot {\mathbf{p}}_k\\ {\overline{\mathbf{r}}}_{k+1}={\overline{\mathbf{r}}}_k-{\alpha }_k{\mathbf{A}}^T\cdot {\overline{\mathbf{p}}}_k\\ {\beta }_k=\frac{{\overline{\mathbf{r}}}_{k+1}\cdot {\mathbf{r}}_{k+1}}{{\overline{\mathbf{r}}}_k\cdot {\mathbf{r}}_k}\\ {\mathbf{p}}_{k+1}={\mathbf{r}}_{k+1}+{\beta }_k{\mathbf{p}}_k\\ {\overline{\mathbf{p}}}_{k+1}={\overline{\mathbf{r}}}_{k+1}+{\beta }_k{\overline{\mathbf{p}}}_k\end{array}$$

这些向量序列满足双正交条件（biorthogonality condition）：

$$\begin{array}{r}{\overline{\mathbf{r}}}_i\cdot {\mathbf{r}}_j={\mathbf{r}}_i\cdot {\overline{\mathbf{r}}}_j=0,j<i\end{array}$$

以及双共轭条件（biconjugacy condition）：

$$\begin{array}{r}{\overline{\mathbf{p}}}_i\cdot \mathbf{A}\cdot {\mathbf{p}}_j={\mathbf{p}}_i\cdot {\mathbf{A}}^T\cdot {\overline{\mathbf{p}}}_j=0,j<i\end{array}$$

此外还有互正交性（mutual orthogonality）：

$$\begin{array}{r}{\overline{\mathbf{r}}}_i\cdot {\mathbf{p}}_j={\mathbf{r}}_i\cdot {\overline{\mathbf{p}}}_j=0,j<i\end{array}$$

这些性质的证明可通过直接归纳法完成 [12]。只要递推过程中分母不为零（即未提前中断），该过程必在 $m\le N$ 步后终止，此时 ${\mathbf{r}}_m={\overline{\mathbf{r}}}_m=0$。这本质上是因为在最多 $N$ 步之后，你已无法再构造出与已有向量正交的新方向。

要使用该算法求解方程组 (2.7.29)，首先对解给出一个初始猜测 ${\mathbf{x}}_0$。令 ${\mathbf{r}}_0$ 为残差：

$${\mathbf{r}}_0=\mathbf{b}-\mathbf{A}\cdot {\mathbf{x}}_0$$

并选择 ${\overline{\mathbf{r}}}_0={\mathbf{r}}_0$。然后生成一系列改进的近似解：

$${\mathbf{x}}_{k+1}={\mathbf{x}}_k+{\alpha }_k{\mathbf{p}}_k$$

同时执行递推关系 (2.7.32)。方程 (2.7.37) 保证了递推得到的 ${\mathbf{r}}_{k+1}$ 实际上就是对应于 ${\mathbf{x}}_{k+1}$ 的残差 $\mathbf{b}-\mathbf{A}\cdot {\mathbf{x}}_{k+1}$。由于 ${\mathbf{r}}_m=0$，因此 ${\mathbf{x}}_m$ 即为方程 (2.7.29) 的解。

尽管对于一般的 $\mathbf{A}$，无法保证整个过程不会中断或变得不稳定，但在实践中这种情况很少发生。更重要的是，最多 $N$ 次迭代后精确终止的性质仅在精确算术下成立。舍入误差意味着你应该将该过程视为一种真正的迭代方法，并在满足某种适当的误差判据时停止迭代。

当 $\mathbf{A}$ 对称且选择 ${\overline{\mathbf{r}}}_0={\mathbf{r}}_0$ 时，普通共轭梯度算法即为双共轭梯度算法的特例。此时对所有 $k$ 都有 ${\overline{\mathbf{r}}}_k={\mathbf{r}}_k$ 且 ${\overline{\mathbf{p}}}_k={\mathbf{p}}_k$；你可以省略它们的计算，使算法工作量减半。这种共轭梯度版本可解释为最小化方程 (2.7.30)。如果 $\mathbf{A}$ 除了对称外还是正定的，则该算法理论上不会中断。下面的求解例程 Linbcg 在输入对称矩阵 $\mathbf{A}$ 时确实会退化为普通共轭梯度法，但它仍会执行所有冗余计算。

该通用算法的另一种变体对应于对称但非正定的 $\mathbf{A}$，此时选择 ${\overline{\mathbf{r}}}_0=\mathbf{A}\cdot {\mathbf{r}}_0$ 而非 ${\overline{\mathbf{r}}}_0={\mathbf{r}}_0$。在这种情况下，对所有 $k$ 都有 ${\overline{\mathbf{r}}}_k=\mathbf{A}\cdot {\mathbf{r}}_k$ 且 ${\overline{\mathbf{p}}}_k=\mathbf{A}\cdot {\mathbf{p}}_k$。因此，该算法等价于普通共轭梯度算法，但所有点积 $\mathbf{a}\cdot \mathbf{b}$ 均被替换为 $\mathbf{a}\cdot \mathbf{A}\cdot \mathbf{b}$。它被称为最小残差算法（minimum residual algorithm），因为它对应于对如下函数的连续最小化：

$$\begin{array}{r}\Phi (\mathbf{x})=\frac{1}{2}\mathbf{r}\cdot \mathbf{r}=\frac{1}{2}|\mathbf{A}\cdot \mathbf{x}-\mathbf{b}{|}^2\end{array}$$

其中，连续迭代向量 ${\mathbf{x}}_k$ 在共轭梯度法生成的相同搜索方向集 ${\mathbf{p}}_k$ 上最小化 $\Phi$。该算法已针对非对称矩阵以多种方式进行了推广。广义最小残差法（GMRES；参见 [13,14]）可能是这些方法中最稳健的一种。

注意，式 (2.7.38) 给出

$$\nabla \Phi (\mathbf{x})={\mathbf{A}}^T\cdot (\mathbf{A}\cdot \mathbf{x}-\mathbf{b})$$

对于任意非奇异矩阵 $\mathbf{A}$，${\mathbf{A}}^T\cdot \mathbf{A}$ 是对称正定的。因此，你可能会想通过对如下问题应用普通共轭梯度算法来求解方程 (2.7.29)：

$$({\mathbf{A}}^{\mathbf{T}}\cdot \mathbf{A})\cdot \mathbf{x}={\mathbf{A}}^{\mathbf{T}}\cdot \mathbf{b}$$

不要这样做！矩阵 ${\mathbf{A}}^T\cdot \mathbf{A}$ 的条件数是 $\mathbf{A}$ 的条件数的平方（条件数的定义见 §2.6）。较大的条件数不仅会增加所需的迭代次数，还会限制解所能达到的精度。几乎总是更优的做法是对原始矩阵 $\mathbf{A}$ 应用双共轭梯度法。

到目前为止，我们尚未讨论这些方法的收敛速率。普通共轭梯度法适用于良态矩阵，即“接近”单位矩阵的矩阵。这提示我们将这些方法应用于方程 (2.7.29) 的预处理形式：

$$({\mathrm{A}}^{-1}\cdot \mathrm{A})\cdot \mathrm{x}={\mathrm{A}}^{-1}\cdot \mathrm{b}$$

其思想是：你可能已经能够轻松求解某个与 $\mathbf{A}$ 接近的矩阵 $\tilde{\mathbf{A}}$ 对应的线性系统，此时 ${\tilde{\mathbf{A}}}^{-1}\cdot \mathbf{A}\approx 1$，从而使算法在更少的步骤内收敛。矩阵 $\tilde{\mathbf{A}}$ 被称为预处理器 [9]，此处给出的整体方案称为预处理双共轭梯度法（PBCG）。在下面的代码中，用户提供的例程 atimes 执行稀疏矩阵 $\mathbf{A}$ 与向量的乘法，而用户提供的例程 asolve 执行预处理器 ${\tilde{\mathbf{A}}}^{-1}$ 与向量的乘法。

为高效实现，PBCG 算法引入了额外的两组向量 ${\mathbf{z}}_k$ 和 ${\overline{\mathbf{z}}}_k$，其定义为

$$\mathbf{A}\cdot {\mathbf{z}}_k={\mathbf{r}}_k\mathrm{且}{\mathbf{A}}^T\cdot {\overline{\mathbf{z}}}_k={\overline{\mathbf{r}}}_k$$

并修改了式 (2.7.32) 中 ${\alpha }_k$、${\beta }_k$、${\mathbf{p}}_k$ 和 ${\overline{\mathbf{p}}}_k$ 的定义：

$$\begin{array}{r}{\alpha }_k=\frac{{\overline{\mathbf{r}}}_k\cdot {\mathbf{z}}_k}{{\overline{\mathbf{p}}}_k\cdot \mathbf{A}\cdot {\mathbf{p}}_k}\\ {\beta }_k=\frac{{\overline{\mathbf{r}}}_{k+1}\cdot {\mathbf{z}}_{k+1}}{{\overline{\mathbf{r}}}_k\cdot {\mathbf{z}}_k}\\ {\mathbf{p}}_{k+1}={\mathbf{z}}_{k+1}+{\beta }_k{\mathbf{p}}_k\\ {\overline{\mathbf{p}}}_{k+1}={\overline{\mathbf{z}}}_{k+1}+{\beta }_k{\overline{\mathbf{p}}}_k\end{array}$$

要使用下面的 Linbcg，你需要提供求解辅助线性系统 (2.7.42) 的例程。如果你不知道该用什么作为预处理器 $\tilde{\mathbf{A}}$，那么可以使用 $\mathbf{A}$ 的对角部分，甚至单位矩阵；此时收敛的负担将完全落在双共轭梯度法本身上。

下面的 Linbcg::solve 例程基于 Anne Greenbaum 最初编写的程序。（参见 [11] 获取另一种较不复杂的实现。）有几点细节你需要了解。

何为“良好”的收敛在很大程度上取决于具体应用。因此，solve 例程提供了四种可能性，通过输入参数 itol 进行选择。若 itol=1，当量 $|\mathbf{A}\cdot \mathbf{x}-\mathbf{b}|/|\mathbf{b}|$ 小于输入量 tol 时迭代停止。若 itol=2，所需判据为

$$|{\tilde{\mathbf{A}}}^{-1}\cdot (\mathbf{A}\cdot \mathbf{x}-\mathbf{b})|/|{\tilde{\mathbf{A}}}^{-1}\cdot \mathbf{b}|<\mathrm{tol}$$

若 itol=3，例程使用其自身对 $\mathbf{x}$ 误差的估计，并要求该误差的模除以 $\mathbf{x}$ 的模小于 tol。itol=4 的设置与 itol=3 相同，只是使用误差和 $\mathbf{x}$ 中绝对值最大的分量（即 $L_{\infty }$ 范数）而非向量模（即 $L_2$ 范数）。你可能需要通过实验来确定哪种收敛判据最适合你的问题。

输出时，err 是实际达到的容差。如果返回的迭代次数 iter 未表明已超过允许的最大迭代次数 itmax，则 err 应小于 tol。如果你想继续迭代，只需保留所有返回量不变并再次调用该例程。然而，该例程在调用之间会丢失其对已张成的共轭梯度子空间的记忆，因此你不应强迫它过于频繁地返回（例如，每 $N$ 次迭代返回一次即可）。

linbca.h

struct Linbcg {
    // 用于通过预处理双共轭梯度法求解稀疏线性方程组的抽象基类。
    // 使用时，需声明一个派生类，在其中为你的问题定义方法 atimes 和 asolve，
    // 以及它们所需的所有数据。然后调用 solve 方法。

    virtual void asolve(VecDoub_I &b, VecDoub_O &x, const Int itrnsp) = 0;

    Doub snrm(VecDoub_I &sx, const Int itol);
    // solve 所用的工具函数。
};

void Linbcg::solve(VecDoub_I &b, VecDoub_IO &x, const Int itol, const Doub tol,
                   const Int itmax, Int &iter, Doub &err)

通过迭代双共轭梯度法求解 $\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$，其中给定 $b[\mathrm{0..}n-1]$，求解 $x[\mathrm{0..}n-1]$。输入时，$x[\mathrm{0..}n-1]$ 应设为解的初始猜测（或全零）；itol 为 1、2、3 或 4，指定应用哪种收敛测试（见正文）；itmax 为允许的最大迭代次数；tol 为期望的收敛容差。输出时，$x[\mathrm{0..}n-1]$ 被更新为改进后的解，iter 为实际执行的迭代次数，err 为估计的误差。矩阵 $\mathbf{A}$ 仅通过用户提供的例程 atimes（计算 $\mathbf{A}$ 或其转置与向量的乘积）和 asolve（求解 $\tilde{\mathbf{A}}\cdot \mathbf{x}=\mathbf{b}$ 或 ${\tilde{\mathbf{A}}}^T\cdot \mathbf{x}=\mathbf{b}$，其中 $\tilde{\mathbf{A}}$ 为某个预处理器矩阵，可能是 $\mathbf{A}$ 的平凡对角部分）进行引用。该例程可重复调用（itmax $\le$ n），以监控 err 的下降情况；也可一次性调用并设置足够大的 itmax 值，以确保达到 tol 的收敛精度。

Doub ak, akden, bk, bkden = 1.0, bknum, bnrm, dxnrm, xnrm, znrm, zm1nrm;
const Doub EPS = 1.0e-14;
Int j, n = b.size();
VecDoub p(n), pp(n), r(n), rr(n), z(n), zz(n);
iter = 0;
atimes(x, r, 0);
for (j = 0; j < n; j++) {
    r[j] = b[j] - r[j];
    rr[j] = r[j];
}

// atimes(r, rr, 0);
if (itol == 1) {
    bnrm = snrm(b, itol);
    asolve(r, z, 0);
} else if (itol == 2) {
    asolve(b, z, 0);
    bnrm = snrm(z, itol);
    asolve(r, z, 0);
} else if (itol == 3 || itol == 4) {
    asolve(b, z, 0);
    bnrm = snrm(z, itol);
    asolve(r, z, 0);
}
// 取消注释此行以获得算法的“最小残差”变体。

// asolve 的输入为 r[0..n-1]，输出为 z[0..n-1]；
// 最后的 0 表示应使用矩阵 $\widetilde{\mathbf{A}}$（而非其转置）。

else if (itol <= 2) {
    asolve(b, z, 0);
    bnorm = snr(m, z, itol);
    asolve(r, z, 0);
    bnorm = snr(m, z, itol);
    asolve(r, z, 0);
}
x[j] += ak * k * pp[j];
x[j] += ak * k * pp[j];
r[j] -= ak * k * zz[j];
rr[j] -= ak * k * zz[j];
}
asolve(r, z, 0);
if (itol <= 1)
    err = snr(m, r, itol) / bnrm;
else if (itol <= 2)
    err = snr(m, z, itol) / bnrm;
else if (abs(zminrm - znrm) > EPS * znrm) {
    dxnrm = abs(ak) * snrm(p, itol);
    err = znrm / abs(zminrm - znrm) * dxnrm;
} else {
    err = znr / mbnrm;
    continue;
}
xnrm = snr(m, x, itol);
if (err <= 0.5 * xnrm) err >= xnrm;
else {
    err = znrm / bnrm;
    continue;
}

求解例程使用这个简短的工具函数来计算向量范数：

下面是一个派生类的示例，用于求解形如 $\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$ 的线性方程组，其中矩阵 $\mathbf{A}$ 采用 ${\mathbb{NR}}_{\text{sparseMat}}$ 的压缩列稀疏格式。该示例使用了一个简单的对角预条件子。

struct NRsparseLinbcg : Linbcg {
    NRsparseMat &mat;
    Int n;
    NRsparseLinbcg(NRsparseMat &matrix) : mat(matrix), n(mat.nrows) {}

构造函数仅绑定对稀疏矩阵的引用，使其在 asolve 和 atimes 中可用。要对某个右端项进行求解，只需调用该对象从基类继承的 solve 方法。

    void atimes(VecDoub_I &x, VecDoub_O &r, const Int itrnsp) {
        if (itrnsp) r = mat.atx(x);
        else r = mat.ax(x);
    }
    void asolve(VecDoub_I &b, VecDoub_O &x, const Int itrnsp) {
        Int i, j;
        Doub diag;
        for (i = 0; i < n; i++) {
            diag = 0.0;
            for (j = mat.col_tr[i]; j < mat.col_tr[i + 1]; j++)
                if (mat.row_ind[j] == i) {
                    diag = mat.val[j];
                    break;
                }
            x[i] = (diag != 0.0 ? b[i] / diag : b[i]);
        }
    }
};

矩阵 $\tilde{\mathbf{A}}$ 是 $\mathbf{A}$ 的对角部分。由于转置矩阵具有相同的对角线元素，因此在此示例中未使用标志 itrnsp。

有关使用从 Linbcg 派生的类求解稀疏矩阵问题的另一个示例，请参见 §3.8。

参考文献

Tewarson, R.P. 1973, Sparse Matrices (New York: Academic Press).[1]

Jacobs, D.A.H. (ed.) 1977, The State of the Art in Numerical Analysis (London: Academic Press), Chapter I.3 (by J.K. Reid).[2]

George, A., and Liu, J.W.H. 1981, Computer Solution of Large Sparse Positive Definite Systems (Englewood Cliffs, NJ: Prentice-Hall).[3]

NAG Fortran Library (Oxford, UK: Numerical Algorithms Group), see 2007+, http://www.nag.co.uk.[4]

IMSL Math/Library Users Manual (Houston: IMSL Inc.), see 2007+, http://www.vni.com/products/imsl.[5]

Eisenstat, S.C., Gursky, M.C., Schultz, M.H., and Sherman, A.H. 1977, Yale Sparse Matrix Package, Technical Reports 112 and 114 (Yale University Department of Computer Science).[6]

Bai, Z., Demmel, J., Dongarra, J., Ruhe, A., and van der Vorst, H. (eds.) 2000, Templates for the Solution of Algebraic Eigenvalue Problems: A Practical Guide Ch. 10 (Philadelphia: S.I.A.M.). Online at URL in http://www.cs.ucdavis.edu/~bai/ET/contents.html.[7]

SPARSKIT, 2007+, at http://www-users.cs.umn.edu/~saad/software/SPARSKIT/sparskit.html.[8]

Golub, G.H., and Van Loan, C.F. 1996, Matrix Computations, 3rd ed. (Baltimore: Johns Hopkins University Press), Chapters 4 and 10, particularly §10.2–§10.3.[9]

Stoer, J., and Bulirsch, R. 2002, Introduction to Numerical Analysis, 3rd ed. (New York: Springer), Chapter 8.[10]

Baker, L. 1991, More C Tools for Scientists and Engineers (New York: McGraw-Hill).[11]

Fletcher, R. 1976, in Numerical Analysis Dundee 1975, Lecture Notes in Mathematics, vol. 506, A. Dold and B. Eckmann, eds. (Berlin: Springer), pp. 73–89.[12]

PCGPAK User's Guide (New Haven: Scientific Computing Associates, Inc.).[13]

Saad, Y., and Schulz, M. 1986, SIAM Journal on Scientific and Statistical Computing, vol. 7, pp. 856–869.[14]

Ueberhuber, C.W. 1997, Numerical Computation: Methods, Software, and Analysis, 2 vols. (Berlin: Springer), Chapter 13.

Bunch, J.R., and Rose, D.J. (eds.) 1976, Sparse Matrix Computations (New York: Academic Press).

Duff, I.S., and Stewart, G.W. (eds.) 1979, Sparse Matrix Proceedings 1978 (Philadelphia: S.I.A.M.).

2.8 范德蒙矩阵与托普利茨矩阵

在 §2.4 中，我们特别处理了三对角矩阵的情形，因为这种特殊的线性方程组只需 $O(N)$ 次运算即可求解，而一般的线性问题则需要 $O(N^3)$ 次运算。当存在这类特殊形式时，了解它们非常重要。如果你恰好遇到一个涉及合适特殊类型的矩阵的问题，计算量的节省可能是巨大的。

本节讨论两种特殊类型的矩阵，它们可以在 $O(N^2)$ 次运算内求解——虽不如三对角矩阵高效，但远优于一般情形。（除了运算量之外，这两种类型并无其他共同点。）第一类矩阵称为范德蒙矩阵（Vandermonde matrices），出现在多项式拟合、由矩重构分布以及其他一些问题中。例如，本书 §3.5 中就出现了一个范德蒙问题。第二类矩阵称为托普利茨矩阵（Toeplitz matrices），通常出现在反卷积和信号处理问题中。在本书中，§13.7 就遇到了一个托普利茨问题。

这些并非唯一值得了解的特殊矩阵类型。希尔伯特矩阵（Hilbert matrices）的元素形式为 $a_{ij}=1/(i+j+1)$，其中 $i,j=0,\dots ,N-1$，可通过精确的整数算法求逆，而用其他方法则非常困难，因为它们是著名的病态矩阵（详见 [1]）。§2.7 中讨论的 Sherman-Morrison 和 Woodbury 公式有时可用于将新的特殊形式转化为已知形式。参考文献 [2] 给出了一些其他特殊形式。但我们发现，这些额外的形式不如我们现在讨论的两种常见。

2.8.1 范德蒙矩阵

一个 $N\times N$ 的范德蒙矩阵完全由 $N$ 个任意数 $x_0,x_1,\dots ,x_{N-1}$ 确定，其 $N^2$ 个元素为整数幂 $x_i^j$，其中 $i,j=0,\dots ,N-1$。显然，根据将 $i$ 视为行索引还是列索引，存在两种可能的形式。在前一种情况下，得到的线性方程组如下所示：

$$\left[\begin{array}{lllll}1& x_0& x_0^2& \cdots & x_0^{N-1}\\ 1& x_1& x_1^2& \cdots & x_1^{N-1}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& x_{N-1}& x_{N-1}^2& \cdots & x_{N-1}^{N-1}\end{array}\right]\cdot \left[\begin{array}{l}{c}_0\\ c_1\\ ⋮\\ c_{N-1}\end{array}\right]=\left[\begin{array}{l}{y}_0\\ y_1\\ ⋮\\ y_{N-1}\end{array}\right]$$

执行矩阵乘法后，你会发现该方程求解的是未知系数 $c_i$，这些系数使得一个多项式能够拟合给定的 $N$ 对横纵坐标 $(x_j,y_j)$。这一问题将在 §3.5 中出现，那里给出的例程将使用我们即将描述的方法来求解方程 (2.8.1)。

另一种对行和列的识别方式会导出如下方程组：

$$\left[\begin{array}{llll}1& 1& \cdots & 1\\ x_0^1& x_1^1& \cdots & x_{N-1}^1\\ x_0^2& x_1^2& \cdots & x_{N-1}^2\\ ⋮& ⋮& \ddots & ⋮\\ x_0^{N-1}& x_1^{N-1}& \cdots & x_{N-1}^{N-1}\end{array}\right]\cdot \left[\begin{array}{l}{w}_0\\ w_1\\ w_2\\ ⋮\\ w_{N-1}\end{array}\right]=\left[\begin{array}{l}{q}_0\\ q_1\\ q_2\\ ⋮\\ q_{N-1}\end{array}\right]$$

将其展开后，你会发现它与矩问题（problem of moments）相关：给定 $N$ 个点 $x_i$ 的值，求未知的权重 $w_i$，使得它们能够匹配前 $N$ 阶矩的给定值 $q_j$。（关于该问题的更多内容，请参阅 [3]。）本节给出的例程用于求解方程 (2.8.2)。

方程 (2.8.1) 和 (2.8.2) 的求解方法与拉格朗日（Lagrange）多项式插值公式密切相关，尽管我们直到 §3.2 才会正式介绍该公式。不过，下面的推导应当是可以理解的：

令 $P_j(x)$ 为如下定义的 $N-1$ 次多项式：

$$P_j(x)=\prod _{n=0}^{N-1}\frac{x-x_n}{x_j-x_n}=\sum _{k=0}^{N-1}{A}_{jk}{x}^k$$

此处最后一个等号的含义是：当乘积展开并合并同类项后，所得到的系数即定义为矩阵 $A_{ij}$ 的元素。

多项式 $P_j(x)$ 通常是关于 $x$ 的函数。但你会注意到，它被特别设计为在所有 $x_i$（其中 $i\ne j$）处取值为零，而在 $x=x_j$ 处取值为 1。换言之，

$$P_j\left(x_i\right)={\delta }_{ij}=\sum _{k=0}^{N-1}{A}_{jk}{x}_i^k$$

但 (2.8.4) 表明，$A_{jk}$ 正是 (2.8.2) 中出现的矩阵 $x_i^k$（下标为列索引）的逆矩阵。因此，(2.8.2) 的解就是该逆矩阵乘以右侧向量：

$$w_j=\sum _{k=0}^{N-1}{A}_{jk}{q}_k$$

至于转置问题 (2.8.1)，我们可以利用“转置的逆等于逆的转置”这一事实，因此有：

$$c_j=\sum _{k=0}^{N-1}{A}_{kj}{y}_k$$

§3.5 中的例程正是基于此实现的。

接下来需要找到一种高效的方法，将 (2.8.3) 中的单项式项展开，以获得矩阵 $A_{jk}$ 的元素。这本质上是一个簿记（bookkeeping）问题，我们将让你自行阅读例程代码，以了解其具体实现方式。其中的一个技巧是定义一个主多项式 $P(x)$：

$$P(x)\equiv \prod _{n=0}^{N-1}(x-x_n)$$

先计算出它的系数，然后通过对多余的单项 $(x-x_j)$ 进行综合除法（synthetic division），得到各个特定 $P_j(x)$ 的分子和分母。（有关综合除法的更多内容，参见 §5.1。）由于每次除法的计算量仅为 $O(N)$，因此整个过程的复杂度为 $O(N^2)$。

需要提醒的是，范德蒙（Vandermonde）系统本质上是严重病态的。（顺便提一下，这与 §5.8 中将要讨论的内容相关：其原因与切比雪夫（Chebyshev）拟合之所以异常精确的原因相同——存在一些高阶多项式，它们在整体上非常接近于零。因此，舍入误差可能会引入这些多项式高阶项的相当大的系数。）因此，建议始终以双精度或更高精度来计算范德蒙问题。

下面用于求解 (2.8.2) 的例程归功于 G.B. Rybicki。

void vander(VecDoub_I &x, VecDoub_O &w, VecDoub_I &q)

求解范德蒙线性方程组 ${\sum }_{i=0}^{N-1}{x}_i^k{w}_i=q_k$（$k=0,\dots ,N-1$）。输入为向量 x[0..n-1] 和 q[0..n-1]；输出为向量 w[0..n-1]。

Int i,j,k,n=q.size();
Doub b,s,t,xx;
VecDoub c(n);
if (n == 1) w[0]=q[0];
else {
    for (i=0;i<n;i++) c[i]=0.0;
    c[n-1] = -x[0];
    for (i=1;i<n;i++) {
        xx = -x[i];
        for (j=(n-1-i);j<(n-1);j++) c[j] += xx*c[j+1];
        c[n-1] += xx;
    }
    for (i=0;i<n;i++) {
        // 依次处理每个子因子
    }
}

2.8.2 Toeplitz 矩阵

一个 $N\times N$ 的 Toeplitz 矩阵由 $2N-1$ 个数 $R_k$ 确定，其中索引 $k$ 的取值范围为 $k=-N+1,\dots ,-1,0,1,\dots ,N-1$。这些数被放置在矩阵中，使得每条从左上到右下的对角线上的元素均为常数：

$$\left[\begin{array}{llllll}{R}_0& R_{-1}& R_{-2}& \cdots & R_{-(N-2)}& R_{-(N-1)}\\ R_1& R_0& R_{-1}& \cdots & R_{-(N-3)}& R_{-(N-2)}\\ R_2& R_1& R_0& \cdots & R_{-(N-4)}& R_{-(N-3)}\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ R_{N-2}& R_{N-3}& R_{N-4}& \cdots & R_0& R_{-1}\\ R_{N-1}& R_{N-2}& R_{N-3}& \cdots & R_1& R_0\end{array}\right]$$

因此，线性 Toeplitz 问题可写作：

$$\sum _{j=0}^{N-1}{R}_{i-j}{x}_j=y_i(i=0,\dots ,N-1)$$

其中 $x_i$（$j=0,\dots ,N-1$）是待求解的未知数。

若对所有 $k$ 均有 $R_k=R_{-k}$，则 Toeplitz 矩阵是对称的。Levinson [4] 提出了一种通过“加边法”（bordering method）快速求解对称 Toeplitz 问题的算法。该方法是一种递归过程，依次求解 $(M+1)$ 维的 Toeplitz 问题：

$$\sum _{i=0}^M{R}_{i-j}{x}_j^{(M)}=y_i(i=0,\dots ,M)$$

其中 $M$ 从 0 开始，依次取 $M=0,1,\dots$，直到最终达到 $M=N-1$，即得到所求结果。向量 $x_j^{(M)}$ 是第 $M$ 步的结果，只有当 $M=N-1$ 时才成为最终答案。

Levinson 方法在标准教材中已有详细记载（例如 [5]）。然而，该方法可推广至非对称情形这一有用事实似乎较少为人所知。因此，为避免过度简略，我们在此给出 G.B. Rybicki 提出的推导过程。

在从第 $M$ 步递推到第 $M+1$ 步时，我们发现当前的解 $x^{(M)}$ 按如下方式变化：

$$\sum _{i=0}^M{R}_{i-j}{x}_j^{(M)}=y_{i}i=0,\dots ,M$$

变为

$$\sum _{j=0}^M{R}_{i-j}{x}_j^{(M+1)}+R_{i-(M+1)}{x}_{M+1}^{(M+1)}=y_{i}i=0,\dots ,M+1$$

通过消去 $y_i$，我们得到

$$\sum _{j=0}^M{R}_{i-j}\left(\frac{x_j^{(M)}-x_j^{(M+1)}}{x_{M+1}^{(M+1)}}\right)=R_{i-(M+1)}i=0,\dots ,M$$

或者通过变量替换 $i\to M-i$ 和 $j\to M-j$，得到

$$\sum _{j=0}^M{R}_{j-i}{G}_j^{(M)}=R_{-(i+1)}$$

其中

$$G_j^{(M)}\equiv \frac{x_{M-j}^{(M)}-x_{M-j}^{(M+1)}}{x_{M+1}^{(M+1)}}$$

换一种说法，

$$x_{M-i}^{(M+1)}=x_{M-i}^{(M)}-x_{M+1}^{(M+1)}{G}_i^{(M)}i=0,\dots ,M$$

因此，如果我们能通过递推得到 $M$ 阶量 $x^{(M)}$ 和 $G^{(M)}$，以及单个 $M+1$ 阶量 $x_{M+1}^{(M+1)}$，那么其余所有的 $x_j^{(M+1)}$ 都可以随之确定。幸运的是，量 $x_{M+1}^{(M+1)}$ 可由方程 (2.8.12) 在 $i=M+1$ 时得到：

$$\sum _{j=0}^M{R}_{M+1-j}{x}_j^{(M+1)}+R_0{x}_{M+1}^{(M+1)}=y_{M+1}$$

对于未知的 $M+1$ 阶量 $x_j^{(M+1)}$，我们可以利用前一阶的 $G$ 量进行替换，因为

$$G_{M-j}^{(M)}=\frac{x_j^{(M)}-x_j^{(M+1)}}{x_{M+1}^{(M+1)}}$$

该操作的结果为

$$x_{M+1}^{(M+1)}=\frac{{\sum }_{j=0}^M{R}_{M+1-j}{x}_j^{(M)}-y_{M+1}}{{\sum }_{j=0}^M{R}_{M+1-j}{G}_{M-j}^{(M)}-R_0}$$

剩下的唯一问题是建立 $G$ 的递推关系。然而，在此之前，我们应指出：对于非对称矩阵的原始线性问题，实际上存在两组不同的解，即我们一直在讨论的右端解（right-hand solutions）和左端解（left-hand solutions）$z_i$。左端解的形式体系仅在于处理如下方程：

$$\sum _{j=0}^M{R}_{j-i}{z}_j^{(M)}=y_{i}i=0,\dots ,M$$

对这组方程执行相同的推导步骤，可得

$$\sum _{j=0}^M{R}_{i-j}{H}_j^{(M)}=R_{i+1}$$

其中

$$H_j^{(M)}\equiv \frac{z_{M-j}^{(M)}-z_{M-j}^{(M+1)}}{z_{M+1}^{(M+1)}}$$

（与式 (2.8.14)–(2.8.15) 对比）。之所以在此提及左端解，是因为根据式 (2.8.21)，$H_j$ 满足的方程与 $x_j$ 的方程完全相同，只是方程右边将 $y_i$ 替换为 $R_{i+1}$。因此，我们可以直接从式 (2.8.19) 推出

$$H_{M+1}^{(M+1)}=\frac{{\sum }_{j=0}^M{R}_{M+1-j}{H}_j^{(M)}-R_{M+2}}{{\sum }_{j=0}^M{R}_{M+1-j}{G}_{M-j}^{(M)}-R_0}$$

同理，$G$ 满足与 $z$ 相同的方程，只需将 $y_i$ 替换为 $R_{-(i+1)}$。由此得到

$$G_{M+1}^{(M+1)}=\frac{{\sum }_{j=0}^M{R}_{j-M-1}{G}_j^{(M)}-R_{-M-2}}{{\sum }_{j=0}^M{R}_{j-M-1}{H}_{M-j}^{(M)}-R_0}$$

同样的“同态”变换也将方程 (2.8.16) 及其关于 $z$ 的对应方程转化为最终形式：

$$\begin{array}{r}{G}_j^{(M+1)}=G_j^{(M)}-G_{M+1}^{(M+1)}{H}_{M-j}^{(M)}\\ H_i^{(M+1)}=H_i^{(M)}-H_{M+1}^{(M+1)}{G}_{M-j}^{(M)}\end{array}$$

现在，从初始值

$$x_0^{(0)}=y_0/R_0{G}_0^{(0)}=R_{-1}/R_0{H}_0^{(0)}=R_1/R_0$$

出发，我们可以递归地进行计算。在每一阶段 $M$，我们利用方程 (2.8.23) 和 (2.8.24) 求出 $H_{M+1}^{(M+1)}$ 和 $G_{M+1}^{(M+1)}$，然后利用方程 (2.8.25) 求出 $H^{(M+1)}$ 和 $G^{(M+1)}$ 的其余分量。由此可轻松计算出向量 $x^{(M+1)}$ 和/或 $z^{(M+1)}$。

下面的程序实现了这一过程。它将 (2.8.25) 中的第二个方程改写为

$$H_{M-i}^{(M+1)}=H_{M-i}^{(M)}-H_{M+1}^{(M+1)}{G}_i^{(M)}$$

以便能够“原地”完成计算。

注意，若 $R_0=0$，上述算法将失效。事实上，由于边界法不允许选主元，只要原始 Toeplitz 矩阵的任意一个对角主子式为零，算法就会失败。（可与 §2.4 中关于三对角算法的讨论进行比较。）如果算法失败，你的矩阵未必是奇异的——你可能只需要改用更慢但更通用的算法，例如带选主元的 $LU$ 分解。

实现方程 (2.8.23)–(2.8.27) 的例程同样归功于 Rybicki。注意，该例程中的 r[n-1+j] 对应于上文的 $R_j$，因此数组 r 的下标范围为 $0$ 到 $2N-2$。

toeplz.h

求解 Toeplitz 方程组 ${\sum }_{j=0}^{N-1}{R}_{(N-1+i-j)}{x}_j=y_i$（$i=0,\dots ,N-1$）。Toeplitz 矩阵无需对称。输入数组为 $y[\mathrm{0..}n-1]$ 和 $r[\mathrm{0..2}\ast n-2]$；输出数组为 $x[\mathrm{0..}n-1]$。

$$n1=\mathrm{n}-1$$

if (r[n1] == 0.0) throw("toeplz-1 singular principal minor");
x[0] = y[0] / r[n1]; // 初始化递归
if (n1 == 0) return;
VecDoub g(n1), h(n1);
g[0] = r[n1 - 1] / r[n1];
h[0] = r[n1 + 1] / r[n1];
for (m = 0; m < n1; m++) {
    m1 = m + 1;
    sxn = -y[m1];
    sd = -r[n1];
    for (j = 0; j < m1; j++) {
        sxn += r[n1 + m1 - j] * x[j];
        sd += r[n1 + m1 - j] * g[m - j];
    }
    if (sd == 0.0) throw("toeplz-2 singular principal minor");
    x[m1] = sxn / sd;
    for (j = 0; j < m1; j++) {
        x[j] -= x[m1] * g[m - j];
    }
    if (m1 == n1) return;
    sgn = -r[n1 - m1 - 1];
    shn = -r[n1 + m1 + 1];
    sgd = -r[n1];
    for (j = 0; j < m1; j++) {
        sgn += r[n1 + j - m1] * g[j];
        shn += r[n1 + m1 - j] * h[j];
        sgd += r[n1 + j - m1] * h[m - j];
    }
    if (sgd == 0.0) throw("toeplz-3 singular principal minor");
    g[m1] = sgn / sgd;
    h[m1] = shn / sd;
    k = m;
    m2 = (m + 2) >> 1;
    pp = g[m1];
    qq = h[m1];
    for (j = 0; j < m2; j++) {
        pt1 = g[j];
        pt2 = g[k];
        qt1 = h[j];
        qt2 = h[k];
        g[j] = pt1 - pp * qt2;
        g[k] = pt2 - pp * qt1;
        h[j] = qt1 - qq * pt2;
        h[k--] = qt2 - qq * pt1;
    }
}
throw("toeplz - should not arrive here!");

如果你需要求解非常大的 Toeplitz 方程组，应了解所谓的“新快速”算法，其计算复杂度仅为 $N(\log N{)}^2$ 量级，而 Levinson 方法的复杂度为 $N^2$。这些方法过于复杂，此处不予介绍。Bunch [6] 和 de Hoog [7] 的论文可作为进一步阅读的入口。

参考文献

Golub, G.H., and Van Loan, C.F. 1996, Matrix Computations, 3rd ed. (Baltimore: Johns Hopkins University Press), Chapter 5 [also treats some other special forms].

Forsythe, G.E., and Moler, C.B. 1967, Computer Solution of Linear Algebraic Systems (Englewood Cliffs, NJ: Prentice-Hall), §19.[1]

Westlake, J.R. 1968, A Handbook of Numerical Matrix Inversion and Solution of Linear Equations (New York: Wiley).[2]

von Mises, R. 1964, Mathematical Theory of Probability and Statistics (New York: Academic Press), pp. 394ff.[3]

Levinson, N., Appendix B of N. Wiener, 1949, Extrapolation, Interpolation and Smoothing of Stationary Time Series (New York: Wiley).[4]

Robinson, E.A., and Treitel, S. 1980, Geophysical Signal Analysis (Englewood Cliffs, NJ: Prentice Hall), pp. 163ff.[5]

Bunch, J.R. 1985, "Stability of Methods for Solving Toeplitz Systems of Equations," SIAM Journal on Scientific and Statistical Computing, vol. 6, pp. 349–364.[6]

de Hoog, F. 1987, “A New Algorithm for Solving Toeplitz Systems of Equations,” Linear Algebra and Its Applications, vol. 88/89, pp. 123–138.[7]

2.9 Cholesky 分解

若一个方阵 $A$ 恰好是对称且正定的，则它具有特殊的、更高效的三角分解。对称意味着对所有 $i,j=0,\dots ,N-1$，有 $a_{ij}=a_{ji}$；正定意味着对所有非零向量 $\mathbf{v}$，

$$\mathbf{v}\cdot \mathbf{A}\cdot \mathbf{v}>0$$

（在第11章中，我们将看到“正定”具有等价的解释：矩阵 $\mathbf{A}$ 的所有特征值均为正。）尽管对称正定矩阵相当特殊，但在某些应用中却频繁出现，因此了解其特有的分解方法——即 Cholesky 分解——是很有用的。当你能使用它时，Cholesky 分解求解线性方程组的速度大约比其他方法快一倍。

Cholesky 分解并非寻找任意的下三角和上三角因子 $\mathbf{L}$ 和 $\mathbf{U}$，而是构造一个下三角矩阵 $\mathbf{L}$，使其转置 ${\mathbf{L}}^T$ 本身即可作为上三角部分。换句话说，我们将方程 (2.3.1) 替换为：

$$\mathbf{L}\cdot {\mathbf{L}}^T=\mathbf{A}$$

这种分解有时被称为对矩阵 $\mathbf{A}$ “开平方根”，但由于涉及转置，它并非字面意义上的平方根。${\mathbf{L}}^T$ 的元素与 $\mathbf{L}$ 的元素显然满足如下关系：

$$L_{ij}^T=L_{ji}$$

将方程 (2.9.2) 按分量展开，可直接得到类似于方程 (2.3.12)–(2.3.13) 的表达式：

$$L_{ii}={\left(a_{ii}-\sum _{k=0}^{i-1}{L}_{ik}^2\right)}^{1/2}$$

以及

$$L_{ji}=\frac{1}{L_{ii}}\left(a_{ij}-\sum _{k=0}^{i-1}{L}_{ik}{L}_{jk}\right)j=i+1,i+2,\dots ,N-1$$

若按 $i=0,1,\dots ,N-1$ 的顺序应用方程 (2.9.4) 和 (2.9.5)，你会发现右侧出现的 $L$ 元素在需要时早已被确定。此外，仅引用满足 $j\ge i$ 的 $a_{ij}$ 元素。（由于 $\mathbf{A}$ 是对称的，这些元素已包含完整信息。）若存储空间紧张，可以让因子 $\mathbf{L}$ 覆盖 $\mathbf{A}$ 的次对角线部分（即下三角部分但不含对角线），同时保留 $\mathbf{A}$ 的上三角输入值；此时还需一个长度为 $N$ 的额外向量来存储 $\mathbf{L}$ 的对角线部分。该算法的运算量为 $N^3/6$ 次内层循环（每次包含一次乘法和一次减法），外加 $N$ 次平方根运算。如前所述，这比对 $\mathbf{A}$ 进行 LU 分解（此时忽略其对称性）的效率大约高一倍。

你可能会对选主元（pivoting）产生疑问。令人欣慰的是，Cholesky 分解在数值上极其稳定，完全不需要选主元。若分解失败，则表明矩阵 $\mathbf{A}$（或考虑舍入误差后某个非常接近的矩阵）不是正定的。事实上，这是一种高效检验对称矩阵是否正定的方法。（在此应用场景中，你可能希望将下述代码中的 throw 替换为某种不那么剧烈的错误提示方式。）

到目前为止，你应该已经熟悉（即使尚未感到厌倦）我们关于实现分解方法的对象的约定，因此我们将 Cholesky 对象一次性完整列出。其中的方法 elmult 和 elsolve 利用矩阵 $\mathbf{L}$ 执行操作：前者对给定的 $\mathbf{y}$ 计算 $\mathbf{L}\cdot \mathbf{y}=\mathbf{c}$ 并返回 $\mathbf{c}$；后者则对给定的 $\mathbf{c}$ 求解同一方程并返回 $\mathbf{y}$。这些操作在多元高斯分布（§7.4 和 §16.5）及协方差矩阵分析（§15.6）等场景中非常有用。

struct Cholesky {
    // Object for Cholesky decomposition of a matrix A, and related functions.
    Int n;
    MatDoub el;

    Cholesky(MatDoub_I &a) : n(a.nrows()), el(a) {
        // 构造。给定一个正定对称矩阵 a[0..n-1][0..n-1]，构造并存储其 Cholesky 分解 A = L·L^T。
        Int i, j, k;
        VecDoub tmp;
        Doub sum;
        if (el.ncols() != n) throw("need square matrix");
        for (i = 0; i < n; i++) {
            for (j = i; j < n; j++) {
                for (sum = el[i][j], k = i - 1; k >= 0; k--) sum -= el[i][k] * el[j][k];
                if (i == j) {
                    if (sum <= 0.0)
                        // A（考虑舍入误差后）不是正定的
                        throw("Cholesky failed");
                    el[i][i] = sqrt(sum);
                } else
                    el[j][i] = sum / el[i][i];
            }
        }
        for (i = 0; i < n; i++)
            for (j = 0; j < i; j++)
                el[j][i] = 0.;
    }

    void solve(VecDoub_I &b, VecDoub_O &x) {
        // 求解 n 个线性方程 A·x = b，其中 A 是一个正定对称矩阵，其 Cholesky 分解已存储。
        // b[0..n-1] 为输入的右侧向量，解向量返回在 x[0..n-1] 中。
        Int i, k;
        Doub sum;
        if (b.size() != n || x.size() != n) throw("bad lengths in Cholesky");
        for (i = 0; i < n; i++) {
            // 求解 L·y = b，将 y 存入 x。
            for (sum = b[i], k = i - 1; k >= 0; k--) sum -= el[i][k] * x[k];
            x[i] = sum / el[i][i];
        }
        for (i = n - 1; i >= 0; i--) {
            // 求解 L^T·x = y。
            for (sum = x[i], k = i + 1; k < n; k++) sum -= el[k][i] * x[k];
            x[i] = sum / el[i][i];
        }
    }

    void elmult(VecDoub_I &y, VecDoub_O &b) {
        // 计算 L·y = b，其中 L 是存储的 Cholesky 分解中的下三角矩阵。
        // y[0..n-1] 为输入，结果返回在 b[0..n-1] 中。
        Int i, j;
        if (b.size() != n || y.size() != n) throw("bad lengths");
        for (i = 0; i < n; i++) {
            b[i] = 0;
            for (j = 0; j <= i; j++) b[i] += el[i][j] * y[j];
        }
    }

    void elsolve(VecDoub_I &b, VecDoub_O &y) {
        // 求解 L·y = b，其中 L 是存储的 Cholesky 分解中的下三角矩阵。
        // b[0..n-1] 为输入的右侧向量，解向量返回在 y[0..n-1] 中。
        Int i, j;
        Doub sum;
        if (b.size() != n || y.size() != n) throw("bad lengths");
        for (i = 0; i < n; i++) {
            for (sum = b[i], j = 0; j < i; j++) sum -= el[i][j] * y[j];
            y[i] = sum / el[i][i];
        }
    }

    void inverse(MatDoub_O &ainv) {
        // 将 ainv[0..n-1][0..n-1] 设为 A 的矩阵逆，其中 A 是已存储其 Cholesky 分解的矩阵。
        Int i, j, k;
        Doub sum;
        ainv.resize(n, n);
        for (i = 0; i < n; i++)
            for (j = 0; j <= i; j++) {
                sum = (i == j ? 1. : 0.);
                for (k = i - 1; k >= j; k--) sum -= el[i][k] * ainv[j][k];
                ainv[j][i] = sum / el[i][i];
            }
        for (i = n - 1; i >= 0; i--)
            for (j = 0; j <= i; j++) {
                sum = (i < j ? 0. : ainv[j][i]);
                for (k = i + 1; k < n; k++) sum -= el[k][i] * ainv[j][k];
                ainv[j][i] = sum / el[i][i];
            }
    }

    Doub logdet() {
        // 返回 A 的行列式的对数，其中 A 是已存储其 Cholesky 分解的矩阵。
        Doub sum = 0.;
        for (Int i = 0; i < n; i++) sum += log(el[i][i]);
        return 2. * sum;
    }
};

参考文献

Wilkinson, J.H., and Reinsch, C. 1971, Linear Algebra, vol. II of Handbook for Automatic Computation (New York: Springer), Chapter I/1.

Gill, P.E., Murray, W., and Wright, M.H. 1991, Numerical Linear Algebra and Optimization, vol. 1 (Redwood City, CA: Addison-Wesley), §4.9.2.

Dahlquist, G., and Bjorck, A. 1974, Numerical Methods (Englewood Cliffs, NJ: Prentice-Hall); reprinted 2003 (New York: Dover), §5.3.5.

Golub, G.H., and Van Loan, C.F. 1996, Matrix Computations, 3rd ed. (Baltimore: Johns Hopkins University Press), §4.2.

2.10 QR 分解

还有一种矩阵分解有时非常有用，即所谓的 QR 分解：

$$\mathbf{A}=\mathbf{Q}\cdot \mathbf{R}$$

其中 $\mathbf{R}$ 是上三角矩阵，而 $\mathbf{Q}$ 是正交矩阵，即满足：

$${\mathbf{Q}}^T\cdot \mathbf{Q}=\mathbf{I}$$

这里 ${\mathbf{Q}}^T$ 是 $\mathbf{Q}$ 的转置矩阵。尽管该分解对一般的矩形矩阵也存在，但我们仅限于讨论所有矩阵均为 $N\times N$ 方阵的情形。

与我们之前遇到的其他矩阵分解方法（如 $LU$、SVD、Cholesky）一样，$QR$ 分解也可用于求解线性方程组。为求解

$$\mathbf{A}\cdot \mathbf{x}=\mathbf{b}$$

首先计算 ${\mathbf{Q}}^T\cdot \mathbf{b}$，然后通过回代法求解

$$\mathbf{R}\cdot \mathbf{x}={\mathbf{Q}}^T\cdot \mathbf{b}$$

由于 $QR$ 分解所需的运算量大约是 $LU$ 分解的两倍，因此它通常不用于一般的线性方程组求解。然而，我们将会遇到一些特殊情况，此时 $QR$ 分解是首选方法。

标准的 $QR$ 分解算法涉及一系列 Householder 变换（将在 §11.3 中详细讨论）。我们将 Householder 矩阵写成 $1-\mathbf{u}\otimes \mathbf{u}/c$ 的形式，其中 $c=\frac{1}{2}\mathbf{u}\cdot \mathbf{u}$。对给定矩阵应用一个适当的 Householder 矩阵，可以将该矩阵某一列中位于选定元素之下的所有元素置零。因此，我们选择第一个 Householder 矩阵 ${\mathbf{Q}}_0$，将 $\mathbf{A}$ 的第 0 列中第 0 个元素以下的所有元素置零。类似地，${\mathbf{Q}}_1$ 将第 1 列中第 1 个元素以下的所有元素置零，依此类推，直到 ${\mathbf{Q}}_{n-2}$。于是有

$$\mathbf{R}={\mathbf{Q}}_{n-2}\cdots {\mathbf{Q}}_0\cdot \mathbf{A}$$

由于 Householder 矩阵是正交的，

$$\mathbf{Q}=({\mathbf{Q}}_{n-2}\cdots {\mathbf{Q}}_0{)}^{-1}={\mathbf{Q}}_0\cdots {\mathbf{Q}}_{n-2}$$

在许多应用中，并不需要显式地构造 $\mathbf{Q}$，仅存储其分解形式（2.10.6）就足够了。（不过，在下面的代码中，我们确实存储了 $\mathbf{Q}$，更准确地说是其转置。）除非矩阵 $\mathbf{A}$ 非常接近奇异，通常不需要选主元。文献 [1] 给出了包含选主元的矩形矩阵通用 $QR$ 算法。对于方阵且不使用选主元的情形，其实现如下：

struct QRdcmp {
    // Object for QR decomposition of a matrix $\mathbf{A}$, and related functions.
    Int n;
    MatDoub qt, r;
    Bool sing;
    QRdcmp(MatDoub_I &a);
    void solve(VecDoub_I &b, VecDoub_O &x);
    void qtmult(VecDoub_I &b, VecDoub_O &x);
    void rsolve(VecDoub_I &b, VecDoub_O &x);
    void update(VecDoub_I &u, VecDoub_I &v);
    void rotate(const Int i, const Doub a, const Doub b);
    // Used by update.
};

与往常一样，构造函数执行实际的分解：

构造矩阵 a[0..n-1][0..n-1] 的 $QR$ 分解。上三角矩阵 $\mathbf{R}$ 和正交矩阵 $\mathbf{Q}$ 的转置被存储起来。如果在分解过程中遇到奇异性，则将 sing 设为 true，但分解仍会完成；否则将其设为 false。

for (k=0; k<n-1; k++) {
    scale = 0.0;
    for (i=k; i<n; i++) scale = MAX(scale, abs(r[i][k])); // Singular case.
    if (scale == 0.0) {
        sing = true;
        c[k] = d[k] = 0.0;
    } else {
        for (i=k; i<n; i++) r[i][k] /= scale;
        Doub sum = 0.0;
        for (i=k; i<n; i++) sum += SQR(r[i][k]);
        Doub sigma = SIGN(sqrt(sum), r[k][k]);
        r[k][k] += sigma;
        c[k] = sigma * r[k][k];
        d[k] = -scale * sigma;
        for (j=k+1; j<n; j++) {
            sum = 0.0;
            for (i=k; i<n; i++) sum += r[i][k] * r[i][j];
            Doub tau = sum / c[k];
            for (i=k; i<n; i++) r[i][j] -= tau * r[i][k];
        }
    }
}
d[n-1] = r[n-1][n-1];
if (d[n-1] == 0.0) sing = true;

// Initialize qt as identity matrix
for (i=0; i<n; i++) {
    for (j=0; j<n; j++) qt[i][j] = 0.0;
    qt[i][i] = 1.0;
}

for (k=0; k<n-1; k++) {
    if (c[k] != 0.0) {
        for (j=0; j<n; j++) {
            Doub sum = 0.0;
            for (i=k; i<n; i++) sum += r[i][k] * qt[i][j];
            sum /= c[k];
            for (i=k; i<n; i++) qt[i][j] -= sum * r[i][k];
        }
    }
}

// Form R explicitly
for (i=0; i<n; i++) {
    r[i][i] = d[i];
    for (j=0; j<i; j++) r[i][j] = 0.0;
}

下一组成员函数用于求解线性方程组。在许多应用中，仅需算法的 (2.10.4) 部分，因此我们将乘法 ${\mathbf{Q}}^T\cdot \mathbf{b}$ 和对 $\mathbf{R}$ 的回代分别放在不同的例程中。

void QRdcmp::rsolve(VecDoub_I &b, VecDoub_O &x) {
    // Solve the triangular set of n linear equations $\mathbf{R} \cdot \mathbf{x} = \mathbf{b}$.
    // b[0..n-1] is input as the right-hand side vector, and x[0..n-1] is returned as the solution vector.

    Int i, j;
    Doub sum;
    if (sing) throw("attempting solve in a singular QR");
    for (i = n-1; i >= 0; i--) {
        sum = b[i];
        for (j = i+1; j < n; j++) sum -= r[i][j] * x[j];
        x[i] = sum / r[i][i];
    }
}

关于如何使用 $QR$ 分解构造正交基以及求解最小二乘问题的细节，请参见 [2]。（出于在病态情形下更强的诊断能力，我们更倾向于使用 SVD，见 §2.6。）

2.10.1 更新 $QR$ 分解

某些数值算法需要依次求解一系列线性方程组，其中每个方程组仅与其前一个略有不同。与其每次都从头开始进行 $O(N^3)$ 次运算来求解方程，不如以 $O(N^2)$ 次运算更新矩阵分解，并利用新的分解来求解下一组线性方程。由于选主元的存在，$LU$ 分解的更新较为复杂。然而，对于一种非常常见的更新形式，

$$\mathbf{A}\to \mathbf{A}+\mathbf{s}\otimes \mathbf{t}$$

（参见公式 2.7.1），$QR$ 分解的更新却相当简单。

在实际应用中，使用等价形式更为方便：

$$\mathbf{A}=\mathbf{Q}\cdot \mathbf{R}\to {\mathbf{A}}^{\prime }={\mathbf{Q}}^{\prime }\cdot {\mathbf{R}}^{\prime }=\mathbf{Q}\cdot (\mathbf{R}+\mathbf{u}\otimes \mathbf{v})$$

利用 $\mathbf{Q}$ 的正交性，可以在公式 (2.10.7) 和 (2.10.8) 之间相互转换，得到

$$\mathbf{t}=\mathbf{v}\text{且}\mathbf{s}=\mathbf{Q}\cdot \mathbf{u}\text{或}\mathbf{u}={\mathbf{Q}}^T\cdot \mathbf{s}$$

该算法 [2] 分为两个阶段。第一阶段应用 $N-1$ 次 Jacobi 旋转（§11.1），将 $\mathbf{R}+\mathbf{u}\otimes \mathbf{v}$ 化为上 Hessenberg 形式。再通过另外 $N-1$ 次 Jacobi 旋转，将该上 Hessenberg 矩阵转化为新的上三角矩阵 ${\mathbf{R}}^{\prime }$。矩阵 ${\mathbf{Q}}^{\prime }$ 即为 $\mathbf{Q}$ 与这 $2(N-1)$ 次 Jacobi 旋转的乘积。在实际应用中，我们通常需要的是 ${\mathbf{Q}}^T$，因此算法被设计为直接操作该矩阵（存储在 QRdcmp 对象中），而非 $\mathbf{Q}$。

void QRdcmp::update(VecDoub_I &u, VecDoub_I &v) {
    // Starting from the stored QR decomposition $\mathbf{A} = \mathbf{Q} \cdot \mathbf{R}$,
    // update it to be the QR decomposition of the matrix $\mathbf{Q} \cdot (\mathbf{R} + \mathbf{u} \otimes \mathbf{v})$.
    // Input quantities are u[0..n-1], and v[0..n-1].

    Int i, k;
    VecDoub w(u);
    for (k = n-1; k >= 0; k--)
        if (w[k] != 0.0) break;
    if (k < 0) k = 0;
    for (i = k-1; i >= 0; i--) {
        rotate(i, w[i], -w[i+1]);
        if (w[i] == 0.0)
            w[i] = abs(w[i+1]);
        else if (abs(w[i]) > abs(w[i+1]))
            w[i] = abs(w[i]) * sqrt(1.0 + SQR(w[i+1]/w[i]));
        else
            w[i] = abs(w[i+1]) * sqrt(1.0 + SQR(w[i]/w[i+1]));
    }

    for (i = 0; i < n; i++) r[0][i] += w[0] * v[i];
    for (i = 0; i < k; i++) {
        rotate(i, r[i][i], -r[i+1][i]);
        if (r[i][i] == 0.0) sing = true;
    }
}

void QRdcmp::rotate(const Int i, const Doub a, const Doub b)

由 update 使用的工具函数。给定矩阵 r[0..n-1][0..n-1] 和 qt[0..n-1][0..n-1]，对这两个矩阵的第 i 行和第 i+1 行执行 Jacobi 旋转。参数 a 和 b 定义了旋转：$\cos \theta =a/\sqrt{a^2+b^2}$，$\sin \theta =b/\sqrt{a^2+b^2}$。

Int j;
Doub c,fact,s,w,y;
if (a == 0.0) {
    c=0.0;
    s=(b >= 0.0 ? 1.0 : -1.0);
} else if (abs(a) > abs(b)) {
    fact=b/a;
    c=SIGN(1.0/sqrt(1.0+(fact*fact)),a);
    s=fact*c;
}
else {
    fact=a/b;
    s=SIGN(1.0/sqrt(1.0+(fact*fact)),b);
    c=fact*s;
}
for (j=i;j<n;j++) {
    y=r[i][j];
    w=r[i+1][j];
    r[i][j]=c*y-s*w;
    r[i+1][j]=s*y+c*w;
}
for (j=0;j<n;j++) {
    y=qt[i][j];
    w=qt[i+1][j];
    qt[i][j]=c*y-s*w;
    qt[i+1][j]=s*y+c*w;
}

我们将在 §9.7 中使用 QR 分解及其更新方法。

参考文献

Wilkinson, J.H., and Reinsch, C. 1971, Linear Algebra, vol. II of Handbook for Automatic Computation (New York: Springer), Chapter I/8.[1]

Golub, G.H., and Van Loan, C.F. 1996, Matrix Computations, 3rd ed. (Baltimore: Johns Hopkins University Press), §5.2, §5.3, §12.5.[2]

2.11 矩阵求逆是一个 $N^3$ 过程吗？

我们以一段轻松的内容结束本章，这是一种算法上的巧妙技巧，它更深入地探讨了矩阵求逆的问题。我们从一个看似简单的问题开始：

计算两个 $2\times 2$ 矩阵相乘需要多少次单独的乘法运算？

$$\begin{array}{r}\left(\begin{array}{ll}{a}_{00}& a_{01}\\ a_{10}& a_{11}\end{array}\right)\cdot \left(\begin{array}{ll}{b}_{00}& b_{01}\\ b_{10}& b_{11}\end{array}\right)=\left(\begin{array}{ll}{c}_{00}& c_{01}\\ c_{10}& c_{11}\end{array}\right)\end{array}$$

八次，对吧？下面是显式写出的乘法：

$$\begin{array}{rl}& c_{00}=a_{00}\times b_{00}+a_{01}\times b_{10}\\ & c_{01}=a_{00}\times b_{01}+a_{01}\times b_{11}\\ & c_{10}=a_{10}\times b_{00}+a_{11}\times b_{10}\\ & c_{11}=a_{10}\times b_{01}+a_{11}\times b_{11}\end{array}$$

你是否认为可以用仅七次乘法写出计算 $c$ 的公式？（在继续阅读之前，自己尝试一下。）

事实上，Strassen [1] 发现了这样一组公式。这些公式是：

$$\begin{array}{rl}& Q_0\equiv (a_{00}+a_{11})\times (b_{00}+b_{11})\\ & Q_1\equiv (a_{10}+a_{11})\times b_{00}\\ & Q_2\equiv a_{00}\times (b_{01}-b_{11})\\ & Q_3\equiv a_{11}\times (-b_{00}+b_{10})\\ & Q_4\equiv (a_{00}+a_{01})\times b_{11}\\ & Q_5\equiv (-a_{00}+a_{10})\times (b_{00}+b_{01})\\ & Q_6\equiv (a_{01}-a_{11})\times (b_{10}+b_{11})\end{array}$$

利用这些中间量，结果为：

$$\begin{array}{r}{c}_{00}=Q_0+Q_3-Q_4+Q_6\\ c_{10}=Q_1+Q_3\\ c_{01}=Q_2+Q_4\\ c_{11}=Q_0+Q_2-Q_1+Q_5\end{array}$$

这有什么用呢？与公式 (2.11.2) 相比，这里少了一次乘法，但多了许多加法和减法。目前还不清楚是否真的有所收益。但请注意，在 (2.11.3) 中，$a$ 和 $b$ 从未交换位置。因此，当 $a$ 和 $b$ 本身是矩阵时，(2.11.3) 和 (2.11.4) 依然成立。现在，两个非常大的矩阵（阶数为 $N=2^m$，其中 $m$ 为整数）相乘的问题可以通过递归地将矩阵划分为四分之一、十六分之一等来解决。关键点在于：节省的不仅仅是“7/8”的因子；而是在递归的每一层都节省了这个因子。总体而言，这将矩阵乘法的复杂度从 $N^3$ 降低到了 $N^{{\log }_{2}7}$。

那么 (2.11.3) – (2.11.4) 中额外的加法呢？它们会不会抵消掉减少乘法带来的优势？对于大的 $N$，(2.11.3) – (2.11.4) 所隐含的加法次数大约是乘法次数的六倍。但是，如果 $N$ 非常大，这个常数因子无法与指数从 $N^3$ 变为 $N^{{\log }_{2}7}$ 所带来的优势相抗衡。

利用这种“快速”矩阵乘法，Strassen 还得到了矩阵求逆的一个令人惊讶的结果 [1]。假设矩阵

$$\begin{array}{r}\left(\begin{array}{ll}{a}_{00}& a_{01}\\ a_{10}& a_{11}\end{array}\right)\mathrm{和}\left(\begin{array}{ll}{c}_{00}& c_{01}\\ c_{10}& c_{11}\end{array}\right)\end{array}$$

互为逆矩阵。那么可以通过以下操作从 $a$ 得到 $c$（参见公式 2.7.11 和 2.7.25）：

$$\begin{array}{rl}& R_0=\mathrm{Inverse}(a_{00})\\ & R_1=a_{10}\times R_0\\ & R_2=R_0\times a_{01}\\ & R_3=a_{10}\times R_2\\ & R_4=R_3-a_{11}\\ & R_5=\mathrm{Inverse}(R_4)\\ & c_{01}=R_2\times R_5\\ & c_{10}=R_5\times R_1\\ & R_6=R_2\times c_{10}\\ & c_{00}=R_0-R_6\\ & c_{11}=-R_5\end{array}$$

在 (2.11.6) 中，“Inverse” 操作仅出现两次。当 $a$ 和 $c$ 是标量时，应将其解释为倒数；当 $a$ 和 $c$ 本身是子矩阵时，则解释为矩阵求逆。想象一下，通过递归地将一个非常大的矩阵（阶数为 $N=2^m$）每次划分为两半来进行求逆。每一步将阶数减半，会使求逆操作的数量翻倍。但这意味着总共只有 $N$ 次除法！因此，在递归使用 (2.11.6) 时，除法并不会成为主导操作。实际上，(2.11.6) 由其中的 6 次乘法主导。既然这些乘法可以用 $N^{{\log }_{2}7}$ 算法完成，那么矩阵求逆也可以！

这很有趣，但我们来看看实际应用：如果你估算一下 $N$ 需要多大，才能使指数从 3 变为 ${\log }_{2}7=2.807$ 所带来的优势足以抵消 Strassen 递归算法复杂性所带来的额外开销，你会发现 $LU$ 分解在短期内并不会被淘汰。然而，快速矩阵乘法例程本身已开始出现在 BLAS 等库中，通常用于 $N\gtrsim 100$ 的情况。

Strassen 最初的矩阵乘法结果已被不断改进。目前已知最快的算法 [2] 的渐近复杂度为 $N^{2.376}$，但实现起来可能并不实际。

如果你喜欢这类趣味问题，可以试试以下两个：(1) 你能否仅用三次实数乘法计算复数 $(a+ib)$ 和 $(c+id)$ 的乘积？[答案：见 §5.5。] (2) 你能否在对许多不同的 $x$ 值求一个一般的四次多项式时，每次求值仅用三次乘法？[答案：见 §5.1。]

参考文献

Coppersmith, D., and Winograd, S. 1990, "Matrix Multiplications via Arithmetic Progressions," Journal of Symbolic Computation, vol. 9, pp. 251–280.[2]

Kronsjö, L. 1987, Algorithms: Their Complexity and Efficiency, 2nd ed. (New York: Wiley).

Winograd, S. 1971, “On the Multiplication of 2 by 2 Matrices,” *Linear Algebra and Its Applications*, vol. 4, pp. 381–388.

Pan, V. Ya. 1980, “New Fast Algorithms for Matrix Operations,” *SIAM Journal on Computing*, vol. 9, pp. 321–342.

Pan, V. 1984, *How to Multiply Matrices Faster*, Lecture Notes in Computer Science, vol. 179 (New York: Springer).

Pan, V. 1984, “How Can We Speed Up Matrix Multiplication?”, *SIAM Review*, vol. 26, pp. 393–415.

[本章解析PDF](/Numerical_Recipes_3rd/Chapter02/model.pdf)