数值计算相关论文&书籍中文翻译

3.0 引言

我们有时知道一个函数 $f(x)$ 在一组点 $x_0,x_1,\dots ,x_{N-1}$（假设 $x_0<\dots <x_{N-1}$）处的值，但却没有一个解析表达式可以让我们计算该函数在任意点的值。例如，这些 $f(x_i)$ 的值可能来自于某些物理测量，或者来自于无法简化为简单函数形式的复杂数值计算。通常这些 $x_i$ 是等间距的，但也不一定。

现在的问题是，以某种方式“画出”一条平滑曲线穿过（甚至延伸超出）这些 $x_i$ 点，从而估计任意 $x$ 处的 $f(x)$ 值。如果所求的 $x$ 位于 $x_i$ 的最大值和最小值之间，则称为插值；如果 $x$ 超出该范围，则称为外推，后者要危险得多（许多前投资分析师可以作证这一点）。

插值和外推方案必须通过某种合理的函数形式来对已知点之间或之外的函数进行建模。这种形式应足够通用，以便能够近似实践中可能出现的大量函数类别。在所使用的函数形式中，多项式（§3.2）是最常见的。有理函数（多项式的商）也被证明极其有用（§3.4）。三角函数（正弦和余弦）则引出了三角插值及相关傅里叶方法，我们将其推迟到第12章和第13章讨论。

数学文献中有大量关于哪些函数能被哪些插值函数良好近似的定理。遗憾的是，这些定理在日常工作中几乎完全无用：如果我们对函数了解得足够多，以至于能应用某个强有力的定理，那我们通常就不会陷入只能根据函数值表格进行插值的窘境！

插值与函数逼近相关，但又有所不同。函数逼近的任务是寻找一个近似但易于计算的函数来替代更复杂的函数。在插值问题中，函数 $f$ 在哪些点上的值是给定的，并非由我们选择；而在函数逼近问题中，我们可以自由选择在哪些点上计算 $f$ 的值，以构建我们的近似。函数逼近将在第5章讨论。

很容易找到一些病态函数，它们会使任何插值方案失效。例如，考虑函数

$$f(x)=3x^2+\frac{1}{{\pi }^4}\ln \left[(\pi -x{)}^2\right]+1$$

该函数在除 $x=\pi$ 外的所有地方都表现良好，在 $x=\pi$ 处仅有轻微的奇异性，但除此之外却能取到所有正负值。任何基于 $x=3.13,3.14,3.15,3.16$ 这些点的插值，对于 $x=3.1416$ 的值都会给出严重错误的结果，尽管绘制这五个点的图形看起来相当平滑！（不妨一试。）

由于病态行为可能潜伏在任何地方，因此非常希望插值和外推程序能提供对其自身误差的估计。当然，这种误差估计绝不可能万无一失。我们可能遇到一个函数，出于只有其创造者才知道的原因，在两个表格点之间突然剧烈且意外地变化。插值总是假设被插值函数具有某种程度的光滑性，但在这一假设框架内，偏离光滑性的行为是可以被检测到的。

从概念上讲，插值过程包含两个阶段：(1)（一次性）拟合一个插值函数到给定的数据点；(2)（可多次）在目标点 $x$ 处计算该插值函数。

然而，这种两阶段方法在实践中通常并不是最佳选择。通常，每次直接从 $N$ 个表格值构造函数估计 $f(x)$ 的方法在计算上更高效，且对舍入误差更不敏感。许多实用方案从一个邻近点 $f(x_i)$ 开始，然后依次加上一系列（希望是递减的）修正项，这些修正项利用了其他邻近点 $f(x_i)$ 的信息。这类过程通常需要 $O(M^2)$ 次运算，其中 $M\ll N$ 是所用局部点的数量。如果一切表现良好，最后一次修正将是最小的，可作为误差的一个非正式（但非严格）上界。在这种方案中，我们也可以说有两个阶段，但现在它们是：(1) 在表格中找到合适的起始位置（$x_i$ 或索引 $i$）；(2) 使用 $M$ 个邻近值（例如以 $x_i$ 为中心）进行插值。

在多项式插值中，有时插值多项式的系数本身是有意义的，尽管用它们来计算插值函数是不推荐的。我们在 §3.5 中讨论这种情况。

使用 $M$ 个最近邻点的局部插值，通常得到的插值函数 $f(x)$ 在一阶或更高阶导数上并不连续。这是因为当 $x$ 越过表格点 $x_i$ 时，插值方案会切换哪些表格点被视为“局部”点。（如果这种切换被允许发生在其他任何位置，那么插值函数本身在该点就会出现不连续。这是个糟糕的主意！）

在需要导数连续性的场合，必须使用所谓的样条函数所提供的“更刚硬”的插值。样条函数在每对表格点之间是一个多项式，但其系数是“略微”非局部地确定的。这种非局部性旨在保证插值函数在全球范围内直到某阶导数都是光滑的。三次样条（§3.3）是最流行的。它们产生的插值函数在二阶导数上是连续的。样条通常比多项式更稳定，在表格点之间出现剧烈振荡的可能性更小。

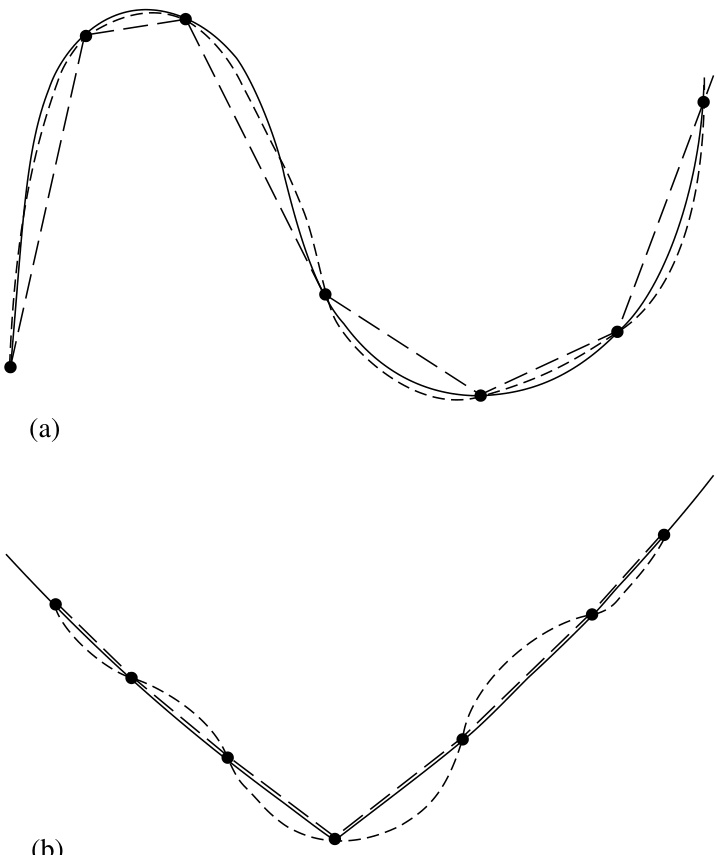
图 3.0.1. (a) 一个光滑函数（实线）用高阶多项式（示意为点线）插值比用低阶多项式（分段线性虚线）更准确。(b) 对于有尖角或高阶导数快速变化的函数，高阶多项式（点线）因过于“刚硬”而不如低阶多项式（虚线）逼近得准确。甚至某些光滑函数，如指数函数或有理函数，也可能被高阶多项式严重误逼近。

插值方案中所用点数 $M$ 减 1 称为插值的阶数。增加阶数并不一定提高精度，尤其是在多项式插值中。如果新增的点远离目标点 $x$，那么得到的高阶多项式由于受到更多约束点的限制，往往会在表格值之间剧烈振荡。这种振荡可能与“真实”函数的行为毫无关系（见图 3.0.1）。当然，增加靠近目标点的点通常会有帮助，但这意味着需要更细密的网格，即更大的函数值表格，而这并不总是可用的。

对于多项式插值而言，最糟糕的 $x_i$ 排列方式恰恰是等间距排列。不幸的是，这恰恰是表格数据最常被采集或呈现的方式。在等间距数据上进行高阶多项式插值是病态的：数据的微小变化可能导致点间振荡的巨大差异。如果被插值的是一个解析函数，且该函数在复平面上某个特定椭圆区域内存在极点（该椭圆的长轴为 $M$ 个点的区间），那么问题尤其严重。即使函数本身在附近没有极点，舍入误差也可能在效果上产生附近的极点，从而导致巨大的插值误差。在 §5.8 中我们会看到，如果你能自由选择一组最优的 $x_i$，这些问题就会消失。但当你拿到一个现成的函数值表格时，这种选择权并不存在。

随着阶数的增加，插值误差通常会先减小，但仅到某一点为止。更高的阶数反而会导致误差急剧增大。

鉴于上述原因，对高阶插值应持谨慎态度。我们强烈推荐使用 3 或 4 个点的多项式插值；对 5 或 6 个点或许可以容忍；但除非有非常严格的误差估计监控，否则我们很少使用更高阶的插值。本章中的大多数插值方法都是分段应用的，每次仅使用 $M$ 个点，因此阶数固定为 $M-1$，无论 $N$ 有多大。如前所述，样条（§3.3）是一种特殊情况，它要求函数及其若干阶导数在相邻区间之间连续，但阶数仍被固定为一个较小的值（通常为 3）。

在 §3.4 中，我们将讨论有理函数插值。在许多（但非全部）情况下，有理函数插值更为稳健，允许使用更高阶数以获得更高精度。然而，标准算法允许在实轴上或复平面附近存在极点。（这不一定是坏事：你可能正试图逼近一个本身就具有此类极点的函数。）一种较新的方法——重心有理插值（§3.4.1）——则抑制了所有附近的极点。这是本章中唯一一种我们可能鼓励尝试高阶（例如 > 6）的方法。重心有理插值与样条相比极具竞争力：其误差通常更小，且得到的近似是无限光滑的（而样条不是）。

下面介绍的插值方法也可用于外推。第17章中的一个重要应用是将其用于常微分方程的积分。在那里，对误差的监控非常谨慎。否则，外推的危险性再怎么强调也不为过：插值函数必然是外推函数，当自变量 $x$ 超出表格值范围（通常超出表格点典型间距的量级，甚至更少）时，它往往会变得完全失控。

插值也可以在多于一维的情况下进行，例如对于函数 $f(x,y,z)$。多维插值通常通过一系列一维插值来实现，但也存在适用于散乱数据的其他技术。我们在 §3.6 – §3.8 中讨论多维方法。

参考文献

Abramowitz, M., and Stegun, I.A. 1964, Handbook of Mathematical Functions (Washington: National Bureau of Standards); 1968年重印 (New York: Dover); 在线版见 http://www.nr.com/aands, §25.2。

Ueberhuber, C.W. 1997, Numerical Computation: Methods, Software, and Analysis, vol. 1 (Berlin: Springer), 第9章。

Stoer, J., and Bulirsch, R. 2002, Introduction to Numerical Analysis, 3rd ed. (New York: Springer), 第2章。

Acton, F.S. 1970, Numerical Methods That Work, 1990, corrected edition (Washington, DC: Mathematical Association of America), Chapter 3.

Johnson, L.W., and Riess, R.D. 1982, Numerical Analysis, 2nd ed. (Reading, MA: Addison-Wesley), Chapter 5.

Ralston, A., and Rabinowitz, P. 1978, A First Course in Numerical Analysis, 2nd ed.; reprinted 2001 (New York: Dover), Chapter 3.

Isaacson, E., and Keller, H.B. 1966, Analysis of Numerical Methods; reprinted 1994 (New York: Dover), Chapter 6.

3.1 预备知识：在有序表中搜索

我们希望定义一个插值对象，该对象了解插值的所有内容，唯独不知道如何实际进行插值！这样，我们就可以将数学上不同的插值方法插入该对象，从而得到具有相同用户接口的不同对象。在此框架中，所有对象共有的一个关键任务是：给定某个特定的值 $x$（即希望计算函数值的位置），在 $x_i$ 表中找到自己的位置。高效地完成这一任务是值得投入精力的；否则，你很容易花费比实际插值更多的时间在表中搜索。

我们用于一维插值的最高层对象是一个抽象基类，其中仅包含一个供用户调用的函数：interp(x) 返回在 $x$ 处的插值函数值。该基类通过声明一个虚函数 rawinterp(jlo, x) “承诺”：每个派生的插值类都将提供一种局部插值方法，该方法在给定表中适当的局部起始点（偏移量 jlo）时进行插值。因此，interp 与 rawinterp 之间的接口必须是一种根据 $x$ 计算 jlo 的方法，即表搜索方法。事实上，我们将使用两种这样的方法。

Int n, mm, jsav, cor, dk;
const Doub *xx, *yy;
Baseinterp(VecDoub_I &x, const Doub *y, Int m)
// 构造函数：为长度为 m 的 x 和 y 表设置插值。通常由派生类调用，而非用户直接调用。
: n(x.size()), mm(m), jsav(0), cor(0), xx(&x[0]), yy(y) {
    j = MIN(1, (int)pow(Doub(n), 0.25));
}
Doub interp(Doub x) {
    // 给定一个值 x，使用 xx 和 yy 指向的数据返回插值结果。
    Int jlo = cor ? hunt(x) : locate(x);
    return rawinterp(jlo, x);
}
Int locate(const Doub x);
Int hunt(const Doub x);
virtual Doub rawinterp(Int jlo, Doub x) = 0;
// 派生类提供此函数作为实际的插值方法。

形式上，问题如下：给定一个横坐标数组 $x_j$（$j=0,\dots ,N-1$），其中横坐标单调递增或单调递减；给定一个整数 $M\le N$ 和一个数值 $x$，求一个整数 $j_{\mathrm{lo}}$，使得 $x$ 在 $M$ 个横坐标 $x_{j_{\mathrm{lo}}},\dots ,x_{j_{\mathrm{lo}}+M-1}$ 中尽可能居中。所谓“居中”是指 $x$ 尽可能位于 $x_m$ 与 $x_{m+1}$ 之间，其中

$$m=j_{\mathrm{lo}}+\lfloor \frac{M-2}{2}\rfloor$$

“尽可能”是指 $j_{\mathrm{lo}}$ 不应小于零，且 $j_{\mathrm{lo}}+M-1$ 不应大于 $N-1$。

在大多数情况下，最终很难比二分法做得更好，因为二分法大约只需 ${\log }_{2}N$ 次尝试即可在表中找到正确位置。

// 给定一个值 x，返回一个值 j，使得 x（尽可能）居中于子范围 xx[j..j+mm-1] 中，
// 其中 xx 是存储的指针。xx 中的值必须是单调的（递增或递减）。
// 返回值不小于 0，也不大于 n-1。
Int ju, jm, jl;
if (n < 2 || mm < 2 || mm > n) throw("locate size error");
Bool ascnd = (xx[n-1] >= xx[0]);
jl = 0;
ju = n-1;
while (ju - jl > 1) {
    jm = (ju + jl) >> 1;
    if ((x >= xx[jm]) == ascnd)
        jl = jm;
    else
        ju = jm;
}
cor = abs(jl - jsav) > DJ ? 0 : 1;
jsav = jl;
return MAX(0, MIN(n - mm, jl - ((mm - 2) >> 1)));

上述 locate 例程通过基类存储的指针访问值数组 xx[]。这种较为原始的访问方式（避免使用如 VecDoub 这样的高级向量类）在此处更可取，原因有二：(1) 通常速度更快；(2) 对于二维插值，我们稍后需要直接指向矩阵的某一行。这种设计选择的风险在于，它假设向量的连续值在内存中连续存储，矩阵单行的连续值也是如此。详见 §1.4.2 的讨论。

3.1.1 相关值的搜索

经验表明，在许多（甚至可能是大多数）应用中，插值例程在连续调用时使用的横坐标几乎相同。例如，你可能正在生成一个用于微分方程右侧的函数：正如我们将在第 17 章看到的，大多数微分方程积分器在求值点上会略有来回跳跃，但其趋势会缓慢地沿积分方向移动。

在这种情况下，每次调用都从头开始进行完整的二分搜索是浪费的。更理想的做法是赋予基类一点智能：如果它发现两次调用“接近”，就预期下一次调用也会接近。当然，如果预测错误，也不应付出过大的代价。

hunt 方法从表中的一个猜测位置开始。它首先以 1、2、4 等步长“搜索”（向上或向下），直到将目标值括入某个区间，然后在该区间内进行二分。最坏情况下，该例程比上述 locate 慢约 2 倍（如果搜索阶段扩展到整个表）。最好情况下，如果目标点通常非常接近输入猜测值，则可比 locate 快 ${\log }_{2}n$ 倍。图 3.1.1 比较了这两种例程。

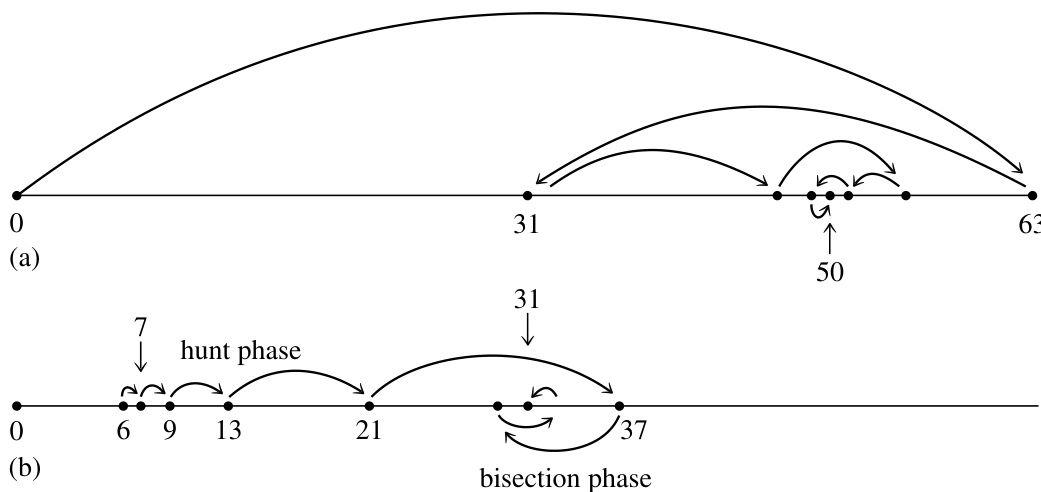
图 3.1.1. 通过二分法查找表项。(a) 在长度为 64 的表中收敛到元素 50 的步骤序列。(b) hunt 例程从表中先前已知的位置开始，以递增步长搜索，然后通过二分收敛。此处展示了一个特别不利的例子：从元素 6 收敛到元素 31。有利的例子是收敛到靠近 6 的元素（如 8），仅需三次“跳跃”。

// 给定一个值 x，返回一个值 j，使得 x（尽可能）居中于子范围 xx[j..j+mm-1] 中，
// 其中 xx 是存储的指针。xx 中的值必须是单调的（递增或递减）。
// 返回值不小于 0，也不大于 n-1。
Int jlsav, jm, ju, inc = 1;
if (n < 2 || mm < 2 || mm > n) throw("hunt size error");
Bool ascnd = (xx[n-1] >= xx[0]);
if (jl < 0 || jl > n-1) {
    jl = 0;
    ju = n-1;
} else {
    if ((x >= xx[jl]) == ascnd) {
        for (;;) {
            ju = jl + inc;
            if (ju >= n-1) { ju = n-1; break; }
            else if ((x < xx[ju]) == ascnd) break;
            else {
                jl = ju;
                inc += inc;
            }
        }
    } else {
        for (;;) {
            jl = jl - inc;
            if (jl <= 0) { jl = 0; break; }
            else if ((x >= xx[jl]) == ascnd) break;
            // 找到括入区间。
            else {
                ju = jl;
                inc += inc;
            }
        }
    }
}
while (ju - jl > 1) {
    jm = (ju + jl) >> 1;
    if ((x >= xx[jm]) == ascnd)
        jl = jm;
    else
        ju = jm;
}
cor = abs(jl - jsav) > DJ ? 0 : 1;
jsav = jl;
return MAX(0, MIN(n - mm, jl - ((mm - 2) >> 1)));

locate 和 hunt 方法都会更新基类中的布尔变量 cor，以指示连续调用是否相关。然后，interp 使用该变量决定下次调用时使用 locate 还是 hunt。当然，这对用户是完全透明的。

3.1.2 示例：线性插值

你可能会认为，到目前为止，我们已经远离了插值方法的主题。为了证明我们仍在正轨上，下面是一个高效实现分段线性插值的类。

你可以通过声明一个实例并传入已填充的横坐标向量 $x_i$ 和函数值向量 $y_i=f(x_i)$ 来构造一个线性插值对象：

Int n = ...;
VecDoub xx(n), yy(n);
...
Linearinterp myfunc(xx, yy);

在幕后，基类构造函数以 $M=2$ 被调用，因为线性插值仅使用包围某个值的两个点。同时，指向数据的指针也被保存下来。（你必须确保向量 xx 和 yy 在 myfunc 被使用期间不会超出作用域。）

当你需要一个插值结果时，只需简单地写：

Doub x, y;
... 
y = myfunc.interp(x);

如果你有多个函数需要插值，则为每个函数分别声明一个 Linear_interp 的实例。

我们现在将使用相同的接口来实现更高级的插值方法。

参考文献

Knuth, D.E. 1997, Sorting and Searching, 3rd ed., vol. 3 of The Art of Computer Programming (Reading, MA: Addison-Wesley), §6.2.1.

3.2 多项式插值与外推

任意两点确定一条唯一的直线；任意三点确定一条唯一的二次曲线；依此类推。通过 $M$ 个点 $y_0=f(x_0),y_1=f(x_1),\dots ,y_{M-1}=f(x_{M-1})$ 的 $M-1$ 次插值多项式可由拉格朗日经典公式显式给出：

$$\begin{array}{rl}& P(x)=\frac{(x-x_1)(x-x_2)\cdots (x-x_{M-1})}{(x_0-x_1)(x_0-x_2)\cdots (x_0-x_{M-1})}{y}_0\\ & +\frac{(x-x_0)(x-x_2)\cdots (x-x_{M-1})}{(x_1-x_0)(x_1-x_2)\cdots (x_1-x_{M-1})}{y}_1+\cdots \\ & +\frac{(x-x_0)(x-x_1)\cdots (x-x_{M-2})}{(x_{M-1}-x_0)(x_{M-1}-x_1)\cdots (x_{M-1}-x_{M-2})}{y}_{M-1}\end{array}$$

该公式包含 $M$ 项，每一项都是一个 $M-1$ 次多项式，并且每一项在除某一个 $x_i$ 之外的所有 $x_i$ 处均为零，而在该点处其值为 $y_i$。

直接实现拉格朗日公式并非大错，但也并不理想。由此得到的算法无法提供误差估计，且编程实现也较为繁琐。一个更好的算法（用于构造相同的、唯一的插值多项式）是 Neville 算法，它与 Aitken 算法密切相关，有时甚至被混淆；而后者如今已被视为过时。

令 $P_0$ 表示通过点 $(x_0,y_0)$ 的零次多项式（即常数）在 $x$ 处的值；因此 $P_0=y_0$。类似地定义 $P_1,P_2,\dots ,P_{M-1}$。再令 $P_{01}$ 表示通过点 $(x_0,y_0)$ 和 $(x_1,y_1)$ 的一次多项式在 $x$ 处的值。类似地定义 $P_{12},P_{23},\dots ,P_{(M-2)(M-1)}$。类似地，对于更高阶的多项式，直到 $P_{012\dots (M-1)}$，即通过全部 $M$ 个点的唯一插值多项式在 $x$ 处的值，也就是我们所求的结果。这些 $P$ 值构成一个“表”，左侧是“祖先”，最终汇聚到最右侧的一个“后代”。例如，当 $M=4$ 时，

$$\begin{array}{rl}{x}_0:& y_0=P_0\\ & P_{01}\\ x_1:& y_1=P_1\\ & P_{12}\\ x_2:& y_2=P_2\\ & P_{123}\\ x_3:& y_3=P_3\end{array}$$

Neville 算法是一种递归方法，按列从左到右依次填充表中的数值。其基础是“子代” $P$ 与其两个“父代”之间的关系：

$$P_{i(i+1)\dots (i+m)}=\frac{(x-x_{i+m})P_{i(i+1)\dots (i+m-1)}+(x_i-x)P_{(i+1)(i+2)\dots (i+m)}}{x_i-x_{i+m}}$$

该递推关系成立，是因为两个父代在点 $x_{i+1},\dots ,x_{i+m-1}$ 处已经一致。

对递推式 (3.2.3) 的一种改进是跟踪父代与子代之间的微小差异，即定义（对于 $m=1,2,\dots ,M-1$）：

$$\begin{array}{r}{C}_{m,i}\equiv P_{i\dots (i+m)}-P_{i\dots (i+m-1)}\\ D_{m,i}\equiv P_{i\dots (i+m)}-P_{(i+1)\dots (i+m)}.\end{array}$$

由此可从 (3.2.3) 推导出以下关系：

$$\begin{array}{r}{D}_{m+1,i}=\frac{(x_{i+m+1}-x)(C_{m,i+1}-D_{m,i})}{x_i-x_{i+m+1}}\\ C_{m+1,i}=\frac{(x_i-x)(C_{m,i+1}-D_{m,i})}{x_i-x_{i+m+1}}\end{array}$$

在每一层 $m$，$C$ 和 $D$ 是使插值精度提高一阶的修正量。最终结果 $P_{0\dots (M-1)}$ 等于任意一个 $y_i$ 加上一组 $C$ 和/或 $D$，这些修正量构成了一条从家族树通向最右侧子代的路径。

以下是实现多项式插值或外推的类。其所有“支撑基础设施”均位于基类 Base_interp 中，它只需提供一个包含 Neville 算法的 rawinterp 方法。

struct Polyinterp : Base_interp

多项式插值对象。构造时传入向量 x 和 y，以及局部使用的点数 $M$（即多项式阶数加一），然后调用 interp 获取插值结果。

{
    Doub dy;
    Polyinterp(VecDoub_I &xv, VecDoub_I &yv, Int m)
        : Base_interp(xv, &yv[0], m), dy(0.) {}
    Doub rawinterp(Int j1, Doub x);
};

Doub Polyinterp::rawinterp(Int j1, Doub x)

给定一个值 x，并利用指向数据 xx 和 yy 的指针，此例程返回插值结果 y，并存储误差估计 dy。返回值通过对子区间 xx[j1..j1+mm-1] 上的 mm 点多项式插值得到。

{
    Int i, m, ns = 0;
    Doub y, den, dif, dift, ho, hp, w;
    const Doub *xa = &xx[j1], *ya = &yy[j1];
    VecDoub c(mm), d(mm);
    dif = abs(x - xa[0]);
    for (i = 0; i < mm; i++) {
        if ((dift = abs(x - xa[i])) < dif) {
            ns = i;
            dif = dift;
        }
        c[i] = ya[i];
        d[i] = ya[i];
    }
    y = ya[ns--];
    for (m = 1; m < mm; m++) {
        // 填充表中的每一列
        for (i = 0; i < mm - m; i++) {
            ho = xa[i] - x;
            // ...（此处省略后续代码）
        }
    }
}

在表格（tableau）中每一列完成后，我们决定将修正量 $c$ 或 $d$ 加入到累积的 $y$ 值中，即决定在表格中选择哪条路径——向上分叉还是向下分叉。我们以这样的方式选择路径：尽可能沿“直线”穿过表格到达其顶点，并相应地更新 $ns$ 以跟踪当前位置。这条路径使得部分近似值尽可能围绕目标值 $x$ 居中。因此，最后加入的 $dy$ 即为误差指示。

Poly_interp 的用户接口与 Linear_interp（见 §3.1 末尾）几乎完全相同，唯一的区别是在构造函数中增加了一个参数用于设定 $M$，即所使用的点数（阶数加一）。一个三次插值器的用法如下所示：

Poly_interp myfunc(xx, yy, 4);

Poly_interp 会为最近一次调用其 interp 函数存储一个误差估计值 dy：

Doub x, y_err;
...
y = myfunc.interp(x);
err = myfunc.dy;

参考文献

Abramowitz, M., and Stegun, I.A. 1964, Handbook of Mathematical Functions (Washington: National Bureau of Standards); 1968年重印版 (New York: Dover); 在线版本见 http://www.nr.com/aands, §25.2。

Stoer, J., and Bulirsch, R. 2002, Introduction to Numerical Analysis, 3rd ed. (New York: Springer), §2.1。

Gear, C.W. 1971, Numerical Initial Value Problems in Ordinary Differential Equations (Englewood Cliffs, NJ: Prentice-Hall), §6.1。

3.3 三次样条插值

给定一个表格函数 $y_i=y(x_i)$，其中 $i=0\dots N-1$，我们聚焦于某一个特定区间，即 $x_j$ 与 $x_{j+1}$ 之间的区间。该区间内的线性插值公式为：

$$y=A{y}_j+B{y}_{j+1}$$

其中

$$A\equiv \frac{x_{j+1}-x}{x_{j+1}-x_j}B\equiv 1-A=\frac{x-x_j}{x_{j+1}-x_j}$$

公式 (3.3.1) 和 (3.3.2) 是通用拉格朗日插值公式 (3.2.1) 的一个特例。

由于它是（分段）线性的，公式 (3.3.1) 在每个区间内部的二阶导数为零，而在节点 $x_j$ 处二阶导数未定义（或为无穷大）。三次样条插值的目标是获得一个插值公式，使其一阶导数光滑、二阶导数连续，无论是在区间内部还是在区间边界处均满足这一性质。

假设（与事实相反）除了已知的函数值 $y_i$ 外，我们还知道函数二阶导数 $y^{\prime \prime }$ 的表格值，即一组数值 $y_i^{\prime \prime }$。那么，在每个区间内，我们可以在公式 (3.3.1) 的右侧加上一个三次多项式，其二阶导数从左侧的 $y_j^{\prime \prime }$ 线性变化到右侧的 $y_{j+1}^{\prime \prime }$。这样处理后，就能得到所需的连续二阶导数。如果我们进一步构造该三次多项式，使其在 $x_j$ 和 $x_{j+1}$ 处取值为零，那么加上它之后就不会破坏插值函数在端点 $x_j$ 和 $x_{j+1}$ 处与表格值 $y_j$ 和 $y_{j+1}$ 的一致性。

稍作推导即可发现，实现上述构造的方式是唯一的，即将 (3.3.1) 替换为：

$$y=A{y}_j+B{y}_{j+1}+C{y}_j^{\prime \prime }+D{y}_{j+1}^{\prime \prime }$$

其中 $A$ 和 $B$ 由 (3.3.2) 定义，而

$$C\equiv \frac{1}{6}(A^3-A)(x_{j+1}-x_j{)}^{2}D\equiv \frac{1}{6}(B^3-B)(x_{j+1}-x_j{)}^2$$

注意，在公式 (3.3.3) 和 (3.3.4) 中，对自变量 $x$ 的依赖完全通过 $A$ 和 $B$ 的线性 $x$-依赖关系体现，而 $C$ 和 $D$ 则通过 $A$ 和 $B$ 表现出对 $x$ 的三次依赖关系。

我们可以很容易验证 $y^{\prime \prime }$ 确实是新插值多项式的二阶导数。对公式 (3.3.3) 关于 $x$ 求导，并利用 $A$、$B$、$C$、$D$ 的定义计算 $dA/dx$、$dB/dx$、$dC/dx$ 和 $dD/dx$，可得一阶导数为：

$$\frac{dy}{dx}=\frac{y_{j+1}-y_j}{x_{j+1}-x_j}-\frac{3A^2-1}{6}(x_{j+1}-x_j)y_j^{\prime \prime }+\frac{3B^2-1}{6}(x_{j+1}-x_j)y_{j+1}^{\prime \prime }$$

二阶导数为：

$$\frac{d^{2}y}{d{x}^2}=A{y}_j^{\prime \prime }+B{y}_{j+1}^{\prime \prime }$$

由于在 $x_j$ 处 $A=1$、$B=0$，而在 $x_{j+1}$ 处则相反，公式 (3.3.6) 表明 $y^{\prime \prime }$ 正是我们所设定的表格二阶导数值，并且二阶导数在相邻区间（例如 $(x_{j-1},x_j)$ 与 $(x_j,x_{j+1})$）的边界处也是连续的。

现在唯一的问题在于，我们假设了 $y_i^{\prime \prime }$ 是已知的，但实际上它们是未知的。然而，我们尚未要求由公式 (3.3.5) 计算出的一阶导数在两个区间边界处连续。三次样条的核心思想正是要求这种连续性，并利用它来建立关于二阶导数 $y_i^{\prime \prime }$ 的方程组。

具体做法是：令公式 (3.3.5) 在区间 $(x_{j-1},x_j)$ 中取 $x=x_j$ 时的值，等于同一公式在区间 $(x_j,x_{j+1})$ 中取 $x=x_j$ 时的值。经过适当整理后，可得（对于 $j=1,\dots ,N-2$）：

$$\frac{x_j-x_{j-1}}{6}{y}_{j-1}^{\prime \prime }+\frac{x_{j+1}-x_{j-1}}{3}{y}_j^{\prime \prime }+\frac{x_{j+1}-x_j}{6}{y}_{j+1}^{\prime \prime }=\frac{y_{j+1}-y_j}{x_{j+1}-x_j}-\frac{y_j-y_{j-1}}{x_j-x_{j-1}}$$

这些方程构成了关于 $N$ 个未知数 $y_i^{\prime \prime }$（$i=0,\dots ,N-1$）的 $N-2$ 个线性方程。因此，存在一个含两个参数的解族。

为了得到唯一解，我们需要额外指定两个条件，通常是在端点 $x_0$ 和 $x_{N-1}$ 处的边界条件。最常见的做法是：

• 将 $y_0^{\prime \prime }$ 和 $y_{N-1}^{\prime \prime }$ 中的一个或两个设为零，从而得到所谓的自然三次样条（natural cubic spline），其在一个或两个边界处的二阶导数为零；或者

• 将 $y_0^{\prime \prime }$ 或 $y_{N-1}^{\prime \prime }$ 设为由公式 (3.3.5) 计算出的值，以使得插值函数的一阶导数在边界处具有指定的值。

尽管自然样条的边界条件被广泛使用，另一种可能性是从表格数据的前几个和后几个点估算端点处的一阶导数值。有关具体实现方法，请参见 §3.7 末尾。当然，最佳做法是能够解析地计算出端点处的一阶导数值。

三次样条之所以特别实用，原因之一是方程组 (3.3.7) 与两个附加边界条件不仅构成线性方程组，而且是三对角（tridiagonal）的。每个 $y_j^{\prime \prime }$ 仅与其相邻的 $j\pm 1$ 处的值耦合。因此，可以使用三对角算法（§2.4）在 $O(N)$ 次运算内求解该方程组。该算法足够简洁，可以直接嵌入构造函数所调用的函数中。

三次样条插值的对象如下所示：

struct Splineinterp : Base_interp
// 三次样条插值对象。用 x 和 y 向量（以及可选的端点一阶导数值）构造，然后调用 interp 获取插值结果。
{
    VecDoub y2;

    Splineinterp(VecDoub_I &xv, VecDoub_I &yv, Doub yp1=1.e99, Doub ypn=1.e99)
        : Base_interp(xv, &yv[0], 2), y2(xv.size())
    {
        sety2(&xv[0], &yv[0], yp1, ypn);
    }

    Splineinterp(VecDoub_I &xv, const Doub *yv, Doub yp1=1.e99, Doub ypn=1.e99)
        : Base_interp(xv, yv, 2), y2(xv.size())
    {
        sety2(&xv[0], yv, yp1, ypn);
    }

    void sety2(const Doub *xv, const Doub *yv, Doub yp1, Doub ypn);
    Doub rawinterp(Int j1, Doub xv);
};

目前你可以忽略第二个构造函数；它将在后续用于二维样条插值。

用户接口与之前的不同之处仅在于增加了两个构造函数参数，用于设置端点处的一阶导数值 $y_0^{\prime }$ 和 $y_{N-1}^{\prime }$。这些参数的默认值被编码为一个很大的数（$1\times 10^{99}$），表示你希望使用自然样条，因此在大多数情况下可以省略。两个构造函数都会调用 sety2 来实际计算并存储二阶导数值。

void Splineinterp::sety2(const Doub *xv, const Doub *yv, Doub yp1, Doub ypn)
// 该例程计算插值函数在由 xv 指向的表格点处的二阶导数，并将结果存储在数组 y2[0..n-1] 中，
// 其中 yv 指向函数值。如果 yp1 和/或 ypn 等于或大于 1e99，则表示在对应边界处使用自然样条边界条件（即二阶导数为零）；
// 否则，它们分别表示端点处的一阶导数值。
{
    Int i, k;
    Doub p, qn, sig, un;
    Int n = y2.size();
    VecDoub u(n - 1);
    if (yp1 > 0.99e99)
        y2[0] = u[0] = 0.0;
    else {
        y2[0] = -0.5;
        u[0] = (3.0 / (xv[1] - xv[0])) * ((yv[1] - yv[0]) / (xv[1] - xv[0]) - yp1);
    }
    for (i = 1; i < n - 1; i++) {
        sig = (xv[i] - xv[i - 1]) / (xv[i + 1] - xv[i - 1]); // 三对角算法。y2 和 u 用于临时存储分解后的因子。
        p = sig * y2[i - 1] + 2.0;
        y2[i] = (sig - 1.0) / p;
        u[i] = (yv[i + 1] - yv[i]) / (xv[i + 1] - xv[i]) - (yv[i] - yv[i - 1]) / (xv[i] - xv[i - 1]);
        u[i] = (6.0 * u[i] / (xv[i + 1] - xv[i - 1]) - sig * u[i - 1]) / p;
    }
    if (ypn > 0.99e99)
        qn = un = 0.0;
    else {
        qn = 0.5;
        un = (3.0 / (xv[n - 1] - xv[n - 2])) * (ypn - (yv[n - 1] - yv[n - 2]) / (xv[n - 1] - xv[n - 2]));
    }
    y2[n - 1] = (un - qn * u[n - 2]) / (qn * y2[n - 2] + 1.0);
    for (k = n - 2; k >= 0; k--)
        y2[k] = y2[k] * y2[k + 1] + u[k];
}

注意，与之前的 Poly_interp 对象不同，Splineinterp 在创建时会存储依赖于你的 $y_i$ 数组内容的数据——即整个向量 y2。虽然我们之前没有特别指出，但之前的插值对象实际上允许用户在运行时修改其 x 和 y 数组的内容（只要长度不变）。但如果你对 Splineinterp 这样做，将得到明显错误的结果！

用户从不直接调用的 rawinterp 方法使用存储的 y2 并实现公式 (3.3.3)：

Doub Splineinterp::rawinterp(Int j1, Doub x)
// 给定一个值 x，利用指向数据 xx 和 yy 的指针以及存储的二阶导数向量 y2，
// 该例程返回三次样条插值结果 y。
{
    Int klo = j1, khi = j1 + 1;
    Doub y, h, b, a;
    h = xx[khi] - xx[klo];
    if (h == 0.0) throw("Bad input to routine splint");
    a = (xx[khi] - x) / h;
    b = (x - xx[klo]) / h;
    y = a * yy[klo] + b * yy[khi] + ((a * a * a - a) * y2[klo] + (b * b * b - b) * y2[khi]) * (h * h) / 6.0;
    return y;
}

典型用法如下：

注意，此处没有可用的误差估计。

参考文献

De Boor, C. 1978, A Practical Guide to Splines (New York: Springer).

Ueberhuber, C.W. 1997, Numerical Computation: Methods, Software, and Analysis, vol. 1 (Berlin: Springer), 第9章。

Forsythe, G.E., Malcolm, M.A., and Moler, C.B. 1977, Computer Methods for Mathematical Computations (Englewood Cliffs, NJ: Prentice-Hall), §4.4 – §4.5。

Stoer, J., and Bulirsch, R. 2002, Introduction to Numerical Analysis, 3rd ed. (New York: Springer), §2.4。

Ralston, A., and Rabinowitz, P. 1978, A First Course in Numerical Analysis, 2nd ed.; 2001年重印版 (New York: Dover), §3.8。

3.4 有理函数插值与外推

某些函数用多项式难以很好地逼近，但用有理函数（即多项式的商）却可以很好地逼近。我们用 $R_{i(i+1)\dots (i+m)}$ 表示一个通过 $m+1$ 个点 $(x_i,y_i),\dots ,(x_{i+m},y_{i+m})$ 的有理函数。更明确地，设

$$R_{i(i+1)\dots (i+m)}=\frac{P_{\mu }(x)}{Q_{\nu }(x)}=\frac{p_0+p_{1}x+\cdots +p_{\mu }{x}^{\mu }}{q_0+q_{1}x+\cdots +q_{\nu }{x}^{\nu }}$$

由于存在 $\mu +\nu +1$ 个未知系数 $p$ 和 $q$（其中 $q_0$ 可任意设定），我们必须满足

$$m+1=\mu +\nu +1$$

在指定一个有理插值函数时，必须同时给出分子和分母的期望阶数。

粗略地说，有理函数有时优于多项式，是因为它们能够对具有极点（即公式 (3.4.1) 中分母的零点）的函数进行建模。这些极点可能出现在实数 $x$ 值处，如果被插值的函数本身就有极点的话。更常见的情况是，函数 $f(x)$ 对所有有限实数 $x$ 都是有限的，但其解析延拓在复平面上存在极点。这些极点本身会破坏多项式逼近的效果，即使该逼近仅限于实数 $x$，正如它们会破坏 $x$ 的无穷幂级数的收敛性一样。如果你在复平面上围绕你的 $m$ 个表格点画一个圆，那么除非最近的极点离该圆相当远，否则你不应期望多项式插值效果良好。相比之下，只要分母中有足够多的 $x$ 的幂次以抵消（消去）附近的极点，有理函数逼近就能保持“良好”。

对于插值问题，有理函数被构造为通过一组选定的表格函数值。不过，我们也应顺便提一下，有理函数逼近也可用于解析工作。有时人们通过如下准则构造有理函数逼近：使公式 (3.4.1) 中的有理函数自身的幂级数展开与目标函数 $f(x)$ 的幂级数展开的前 $m+1$ 项一致。这称为帕德（Padé）逼近，将在 §5.12 中讨论。

Bulirsch 和 Stoer 发现了一种类似于 Neville 型的算法，用于对表格数据进行有理函数外推。该算法逐列构建类似于公式 (3.2.2) 的表，最终得到一个结果和一个误差估计。Bulirsch-Stoer 算法生成所谓的对角有理函数：当 $m$ 为偶数时，分子和分母的次数相等；当 $m$ 为奇数时，分母的次数比分母大一（参见上面的公式 3.4.2）。关于该算法的推导，请参见 [1]。该算法可由一个递推关系总结，该递推关系与多项式逼近的公式 (3.2.3) 完全类似：

$$\begin{array}{r}{R}_{i(i+1)\dots (i+m)}=R_{(i+1)\dots (i+m)}\\ +\frac{R_{(i+1)\dots (i+m)}-R_{i\dots (i+m-1)}}{\left(\frac{x-x_i}{x-x_{i+m}}\right)\left(1-\frac{R_{(i+1)\dots (i+m)}-R_{i\dots (i+m-1)}}{R_{(i+1)\dots (i+m)}-R_{(i+1)\dots (i+m-1)}}\right)-1}\end{array}$$

此递推关系利用通过 $m$ 个点和（公式 3.4.3 中的项 $R_{(i+1)\dots (i+m-1)}$）$m-1$ 个点的有理函数，生成通过 $m+1$ 个点的有理函数。其初始条件为

$$R_i={\gamma }_i$$

以及

$$R\equiv [R_{i(i+1)\dots (i+m)}\mathrm{with}m=-1]=0$$

现在，与上面的公式 (3.2.4) 和 (3.2.5) 完全类似，我们可以将递推关系 (3.4.3) 转换为仅涉及小量差值的形式：

$$\begin{array}{r}{C}_{m,i}\equiv R_{i\dots (i+m)}-R_{i\dots (i+m-1)}\\ D_{m,i}\equiv R_{i\dots (i+m)}-R_{(i+1)\dots (i+m)}\end{array}$$

注意，这些量满足关系式

$$C_{m+1,i}-D_{m+1,i}=C_{m,i+1}-D_{m,i}$$

该关系在证明以下递推公式时很有用：

$$\begin{array}{r}{D}_{m+1,i}=\frac{C_{m,i+1}(C_{m,i+1}-D_{m,i})}{\left(\frac{x-x_i}{x-x_{i+m+1}}\right)D_{m,i}-C_{m,i+1}}\\ C_{m+1,i}=\frac{\left(\frac{x-x_i}{x-x_{i+m+1}}\right)D_{m,i}(C_{m,i+1}-D_{m,i})}{\left(\frac{x-x_i}{x-x_{i+m+1}}\right)D_{m,i}-C_{m,i+1}}\end{array}$$

有理函数插值的类在各方面都与多项式插值的类完全相同，当然，除了 rawinterp 中实现的方法不同。使用方法参见 §3.2 末尾。$M$ 的合理取值范围通常为 4 到 7。

给定一个值 $x$，并使用指向数据 $xx$ 和 $yy$ 的指针，该例程返回一个插值结果 $y$，并存储一个误差估计值 $dy$。返回值是通过对子区间 $xx[j\mathrm{1..}j1+mm-1]$ 上的 $mm$ 点对角有理函数插值得到的。

const Doub TINY = 1.0e-99;
Int m, i, ns = 0;
Doub y, w, t, hh, h, dd;
const Doub *xa = &xx[j1], *ya = &yy[j1];
VecDoub c(mm), d(mm);
hh = abs(x - xa[0]);
for (i = 0; i < mm; i++) {
    h = abs(x - xa[i]);
    if (h == 0.0) {
        dy = 0.0;
        return ya[i];
    } else if (h < hh) {
        ns = i;
        hh = h;
    }
    c[i] = ya[i];
    d[i] = ya[i] + TINY;
}
y = ya[ns];
for (m = 1; m < mm; m++) {
    for (i = 0; i < mm - m; i++) {
        w = c[i + 1] - d[i];
        h = xa[i + m] - x;
        t = (xa[i] - x) * d[i] / h;
        dd = t - c[i + 1];
        if (dd == 0.0) throw("Error in routine ratint");
        // 此错误条件表明插值函数在所请求的 x 值处存在极点。
        dd = w / dd;
        d[i] = c[i + 1] * dd;
        c[i] = t * dd;
    }
    y += (m % 2 == 0 ? c[0] : d[0]);
}
dy = (m % 2 == 0 ? d[0] : c[0]) - y;
return y;

3.4.1 重心有理插值

假设我们尝试使用上述算法，利用所有给定节点 $x_0,x_1,\dots ,x_{N-1}$ 构造整个数据表上的全局近似。一个潜在的缺点是，即使原始函数在该区间内没有极点，近似函数仍可能在插值区间内部出现极点（即公式 (3.4.1) 的分母为零的位置）。一个更严重（且相关）的问题是，我们允许近似的阶数增长到 $N-1$，这很可能过大。

可以推导出一种替代算法 [2]，该算法在整个实轴上均无极点，并且允许将实际近似阶数指定为任意小于 $N$ 的整数 $d$。其技巧在于令公式 (3.4.1) 中分子和分母的次数均为 $N-1$。这要求系数 $p$ 和 $q$ 不再相互独立，因此公式 (3.4.2) 不再成立。

该算法采用有理插值函数的重心形式：

$$R(x)=\frac{\sum _{i=0}^{N-1}\frac{w_i}{x-x_i}{y}_i}{\sum _{i=0}^{N-1}\frac{w_i}{x-x_i}}$$

可以证明，通过适当选择权重 $w_l$，任意有理插值函数均可表示为此形式；作为特例，多项式插值函数也可如此表示 [3]。事实证明，这种形式具有许多优良的数值性质。重心有理插值与样条插值相比极具竞争力：其误差通常更小，且所得近似函数无限光滑（而样条则不然）。

假设我们希望有理插值函数具有近似阶数 $d$，即当节点间距为 $O(h)$ 时，误差在 $h\to 0$ 时为 $O(h^{d+1})$。此时权重的计算公式为：

$$w_k=\sum _{\begin{array}{c}0\le i\le N-d-1\\ i\le k\le i+d\end{array}}(-1{)}^k\prod _{\begin{array}{c}j=i\\ j\ne k\end{array}}^{i+d}\frac{1}{x_k-x_j}$$

例如，

$$\begin{array}{rl}& w_k=(-1{)}^k,d=0\\ & w_k=(-1{)}^{k-1}\left[\frac{1}{x_k-x_{k-1}}+\frac{1}{x_{k+1}-x_k}\right],d=1\end{array}$$

在最后一个公式中，对于 $w_0$ 和 $w_{N-1}$，应省略涉及越界 $x_k$ 值的项。

以下例程实现了重心有理插值。给定 $N$ 个节点和期望阶数 $d$（其中 $d<N$），它首先计算权重 $w_k$。随后对 interp 的调用将使用公式 (3.4.9) 计算插值结果。注意，rawinterp 的参数 $j1$ 未被使用，因为该算法旨在一次性构造整个区间的近似。

计算权重的计算量为 $O(Nd)$ 次运算。对于较小的 $d$，这与样条插值相差不大。但需注意，后续每次插值计算的计算量为 $O(N)$，而非样条插值的 $O(d)$。

struct BaryRatinterp : Base_interp
// 重心有理插值对象。构造对象后，调用 interp 获取插值结果。
// 注意：不计算误差估计 dy。
{
    VecDoub w;
    Int d;
    BaryRatinterp(VecDoub_I &xv, VecDoub_I &yv, Int dd);
    Doub rawinterp(Int j1, Doub x);
    Doub interp(Doub x);
};

BaryRatinterp::BaryRatinterp(VecDoub_I &xv, VecDoub_I &yv, Int dd)
    : Base_interp(xv, &yv[0], xv.size()), w(n), d(dd)
// 构造函数参数为长度为 n 的 x 和 y 向量，以及期望近似的阶数 d。
{
    if (n <= d) throw("d too large for number of points in BaryRat_interp");
    for (Int k = 0; k < n; k++) {
        Int imin = MAX(k - d, 0);
        Int imax = (k >= n - d) ? n - d - 1 : k;
        Doub temp = (imin & 1) ? -1.0 : 1.0;
        Doub sum = 0.0;
        for (Int i = imin; i <= imax; i++) {
            Int jmax = MIN(i + d, n - 1);
            Doub term = 1.0;
            for (Int j = i; j <= jmax; j++) {
                if (j == k) continue;
                term *= (xx[k] - xx[j]);
            }
            term = temp / term;
            temp = -temp;
            sum += term;
        }
        w[k] = sum;
    }
}

Doub BaryRatinterp::rawinterp(Int j1, Doub x)
// 使用公式 (3.4.9) 计算重心有理插值结果。
// 注意：j1 未被使用，因为近似是全局的；
// 仅为了与 Base_interp 兼容而保留该参数。
{
    Doub num = 0.0, den = 0.0;
    for (Int i = 0; i < n; i++) {
        Doub h = x - xx[i];
        if (h == 0.0) {
            return yy[i];
        } else {
            Doub temp = w[i] / h;
            num += temp * yy[i];
            den += temp;
        }
    }
    return num / den;
}

Doub BaryRatinterp::interp(Doub x) {
    // 由于插值是全局的，无需调用 hunt 或 locate，
    // 因此重写 interp 以直接调用 rawinterp，并传入虚拟的 j1 值。
    return rawinterp(0, x);
}

建议先尝试较小的 $d$ 值，再尝试更大的值。

参考文献

Stoer, J., and Bulirsch, R. 2002, Introduction to Numerical Analysis, 3rd ed. (New York: Springer), §2.2.[1]

Floater, M.S., and Hormann, K. 2006+, "Barycentric Rational Interpolation with No Poles and High Rates of Approximation," at http://www.in.tu-clausthal.de/fileadmin/homes/techreports/ifi0606hormann.pdf.[2]

Berrut, J.-P., and Trefethen, L.N. 2004, "Barycentric Lagrange Interpolation," SIAM Review, vol. 46, pp. 501–517.[3]

Gear, C.W. 1971, Numerical Initial Value Problems in Ordinary Differential Equations (Englewood Cliffs, NJ: Prentice-Hall), §6.2.

Cuyt, A., and Wuytack, L. 1987, Nonlinear Methods in Numerical Analysis (Amsterdam: North-Holland), Chapter 3.

3.5 插值多项式的系数

有时你可能希望知道的不是通过（少量！）点的插值多项式的值，而是该多项式的系数。例如，这些系数的一个合理用途可能是同时计算函数及其若干阶导数的插值值（见§5.1），或者将表格函数的一段与另一个函数进行卷积，而该函数的各阶矩（即它与 $x$ 的各次幂的卷积）已知解析表达式。

然而，请务必确认你确实需要这些系数。通常，插值多项式的系数的精度远低于在指定横坐标处计算出的函数值的精度。因此，若只是为了计算插值值而先求出系数，这种做法并不明智。例如，这样计算出的值不会精确通过表格中的点，而§3.1–§3.3中例程计算出的值则会精确通过这些点。

此外，你不应将插值多项式（及其系数）与其“表亲”——数据集的最佳拟合多项式——混淆。拟合是一种平滑过程，因为拟合所用的系数数量通常远少于数据点的数量。因此，即使表格值中存在统计误差，拟合系数仍可被准确且稳定地确定（见§14.9）。而插值中，系数数量与表格点数量相等，它将表格值视为完全精确。如果这些值实际上包含统计误差，那么这些误差可能会在表格点之间被放大，导致插值多项式出现剧烈振荡。

与之前一样，我们设表格点为 $y_i\equiv y(x_i)$。若插值多项式写作

$$y=c_0+c_{1}x+c_2{x}^2+\cdots +c_{N-1}{x}^{N-1}$$

则系数 $c_i$ 需满足线性方程组

$$\begin{array}{r}\left[\begin{array}{llllc}1& x_0& x_0^2& \cdots & x_0^{N-1}\\ 1& x_1& x_1^2& \cdots & x_1^{N-1}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ 1& x_{N-1}& x_{N-1}^2& \cdots & x_{N-1}^{N-1}\end{array}\right]\cdot \left[\begin{array}{l}{c}_0\\ c_1\\ ⋮\\ c_{N-1}\end{array}\right]=\left[\begin{array}{l}{y}_0\\ y_1\\ ⋮\\ y_{N-1}\end{array}\right]\end{array}$$

这是一个范德蒙德（Vandermonde）矩阵，如§2.8所述。原则上，可以使用求解一般线性方程组的标准技术（§2.3）来解方程(3.5.2)；然而，§2.8中推导出的特殊方法效率要高得多，其计算量级约为 $N$ 倍，因此要好得多。

请记住，范德蒙德方程组可能非常病态。在这种情况下，任何数值方法都无法给出非常精确的答案。请注意，这种情况并不意味着使用§3.2中的方法计算插值值会遇到困难，而仅意味着求系数会遇到困难。

与§2.8中的例程一样，以下例程也归功于 G.B. Rybicki。

// polcoef.h

void polcoe(VecDoub_I &x, VecDoub_I &y, VecDoub_O &cof)

给定包含表格函数 $y_i=f(x_i)$ 的数组 x[0..n-1] 和 y[0..n-1]，该例程返回系数数组 cof[0..n-1]，使得 $y_i={\sum }_{j=0}^{n-1}{\text{cof}}_j{x}_i^j$。

{
    Int k, j, i, n = x.size();
    Doub phi, ff, b;
    VecDoub s(n);
    for (i = 0; i < n; i++) s[i] = cof[i] = 0.0;
    s[n-1] = -x[0];
    for (i = 1; i < n; i++) {
        for (j = n-1-i; j < i-1; j++)
            s[j] -= x[i] * s[j+1];
        s[n-1] -= x[i];
    }
    for (j = 0; j < n; j++) {
        phi = n;
        for (k = n-1; k > 0; k--)
            phi = k * s[k] + x[j] * phi;
        ff = y[j] / phi;
        b = 1.0;
        for (k = n-1; k >= 0; k--) {
            cof[k] += b * ff;
            b = s[k] + x[j] * b;
        }
    }
}

3.5.1 另一种方法

另一种技术是利用已给出的函数值插值例程（polint；§3.2）。如果我们对 $x=0$ 进行插值（或外推），显然得到的值就是 $c_0$。接着，我们可以从所有 $y_i$ 中减去 $c_0$，再分别除以其对应的 $x_i$。去掉一个点（例如 $x_i$ 最小的那个点是个不错的选择），重复此过程即可求得 $c_1$，依此类推。

这种方法的稳定性并非显而易见，但我们通常发现它比前述例程稍稳定一些。该方法的复杂度为 $O(N^3)$，而前一种方法为 $O(N^2)$。然而你会发现，由于范德蒙德问题固有的病态性，这两种方法在 $N$ 较大时效果都不佳。在单精度下，$N$ 最多到 8 或 10 是令人满意的；双精度下大约可翻倍。

void polcof(VecDoub_I &xa, VecDoub_I &ya, VecDoub_O &cof)

给定包含表格函数 $y{a}_i=f(x{a}_i)$ 的数组 xa[0..n-1] 和 ya[0..n-1]，该例程返回系数数组 cof[0..n-1]，使得 $y{a}_i={\sum }_{j=0}^{n-1}{\text{cof}}_{j}x{a}_i^j$。

{
    Int k, j, i, n = xa.size();
    Doub xmin;
    VecDoub x(n), y(n);
    for (j = 0; j < n; j++) {
        x[j] = xa[j];
        y[j] = ya[j];
    }
    for (j = 0; j < n; j++) {
        VecDoub x_t(n - j), y_t(n - j);
        for (k = 0; k < n - j; k++) {
            x_t[k] = x[k];
            y_t[k] = y[k];
        }
        Polyinterp interp(x_t, y_t);
        cof[j] = interp.rawinterp(0.0);
        xmin = 1.0e99;
        k = -1;
        for (i = 0; i < n - j; i++) {
            if (abs(x[i]) < xmin) {
                xmin = abs(x[i]);
                k = i;
            }
        }
        for (i = 0; i < n - j; i++) {
            if (x[i] != 0.0)
                y[i] = (y[i] - cof[j]) / x[i];
        }
        for (i = k + 1; i < n - j; i++) {
            y[i - 1] = y[i];
            x[i - 1] = x[i];
        }
    }
}

如果点 $x=0$ 不在（或至少不靠近）表格点 $x_i$ 的范围内，那么插值多项式的系数通常会变得非常大。然而，系数中真正的“信息含量”体现在与“平移引起”的大数值之间的微小差异上。这是病态性的一个来源，会导致有效数字的损失和系数难以准确确定。在这种情况下，你应该考虑重新定义问题的原点，将 $x=0$ 放在一个合理的位置。

另一种病态情况是：如果对一个光滑函数尝试使用过高阶的插值，插值多项式会试图利用其高阶系数，通过大数值且几乎精确抵消的组合，来匹配表格值直至机器精度的极限。这种效应与插值多项式在约束点之间剧烈振荡的固有倾向相同，即使机器的浮点精度无限高，这种现象依然存在。上述两个例程 polcoe 和 polcof 对可能出现的病态情况具有略微不同的敏感性。

你是否仍然确信使用系数是个好主意？

3.6 多维网格上的插值

在多维插值中，我们希望估计一个具有多个自变量的函数 $y(x_1,x_2,\dots ,x_n)$。关键区别在于：我们是否在 $n$ 维网格上拥有完整的表格值集合？还是仅知道 $n$ 维空间中某些散乱点上的函数值？在一维情况下，这个问题从未出现，因为任何一组 $x_i$ 值，只要按升序排列，就可视为有效的（不要求等间距的）一维网格。

随着维数 $n$ 增大，维持完整网格会因网格点数量的爆炸式增长而迅速变得不切实际。此时，§3.7中将讨论的散乱数据方法就成为首选。但不要误以为这类方法本质上比网格方法更精确。通常它们精度更低。就像那条三条腿的狗一样，它们之所以引人注目，是因为它们居然能工作，而不是因为它们一定工作得很好！

在二维情况下，两类方法都是实用的，还有一些其他方法。例如，有限元方法（其中三角剖分最为常见）试图在散乱点上施加某种几何规则结构，并利用该结构进行插值。我们将在§21.6中详细讨论基于三角剖分的二维插值；该节应视为此处讨论的延续。

在本节剩余部分，我们仅考虑网格上的插值情形，并且仅在代码中实现（最常见的）二维情况。所给出的所有方法均可直接推广到三维。在§3.7中实现散乱数据方法时，将处理一般的 $n$ 维情形。

在二维情况下，我们假定给定一个函数值矩阵 $y_{ij}$，其中 $i=0,\dots ,M-1$，$j=0,\dots ,N-1$。同时还给定一个 $x_1$ 值数组 $x_{1i}$ 和一个 $x_2$ 值数组 $x_{2j}$，其中 $i$ 和 $j$ 如前所述。这些输入量与底层函数 $y(x_1,x_2)$ 的关系为

$$y_{ij}=y(x_{1i},x_{2j})$$

我们希望通过插值来估计函数 $y$ 在某个未制表点 $(x_1,x_2)$ 处的值。

一个重要的概念是该点 $(x_1,x_2)$ 所落入的网格单元（grid square），即包围该内点的四个制表点。为方便起见，我们将这四个点按逆时针方向从左下角开始编号为 0 到 3。更精确地说，若

$$\begin{array}{r}{x}_{1i}\le x_1\le x_{1(i+1)}\\ x_{2j}\le x_2\le x_{2(j+1)}\end{array}$$

定义了 $i$ 和 $j$ 的取值，则

$$\begin{array}{rl}& y_0\equiv y_{ij}\\ & y_1\equiv y_{(i+1)j}\\ & y_2\equiv y_{(i+1)(j+1)}\\ & y_3\equiv y_{i(j+1)}\end{array}$$

二维中最简单的插值方法是双线性插值（bilinear interpolation），其公式为：

$$\begin{array}{r}t\equiv (x_1-x_{1i})/(x_{1(i+1)}-x_{1i})\\ u\equiv (x_2-x_{2j})/(x_{2(j+1)}-x_{2j})\end{array}$$

（因此 $t$ 和 $u$ 均在 0 到 1 之间），以及

$$y(x_1,x_2)=(1-t)(1-u)y_0+t(1-u)y_1+tu{y}_2+(1-t)u{y}_3$$

双线性插值通常“对政府工作来说已经足够好了”。当插值点从一个网格单元移动到另一个时，插值函数值是连续变化的。然而，插值函数的梯度在每个网格单元的边界处会发生不连续的变化。

我们可以轻松地通过复用一维插值类中的部分“机制”来实现一个双线性插值对象：

struct Bilininterp {
    // 用于矩阵上的双线性插值的对象。
    // 构造时传入 x1 值的向量、x2 值的向量，以及制表函数值 y_{ij} 的矩阵。
    // 然后调用 interp 获取插值结果。
    Int m, n;
    const MatDoub &y;
    Linearinterp x1terp, x2terp;

    Bilininterp(VecDoub_I &x1v, VecDoub_I &x2v, MatDoub_I &ym)
        : m(x1v.size()), n(x2v.size()), y(ym),
          x1terp(x1v, x1v), x2terp(x2v, x2v) {}
    // 构造两个虚拟的一维插值对象，仅用于其 locate 和 hunt 函数。

    Doub interp(Doub x1p, Doub x2p) {
        Int i, j;
        Doub yy, t, u;
        i = x1terp.cor ? x1terp.hunt(x1p) : x1terp.locate(x1p);
        j = x2terp.cor ? x2terp.hunt(x2p) : x2terp.locate(x2p);
        // 找到所在的网格单元。
        t = (x1p - x1terp.xx[i]) / (x1terp.xx[i+1] - x1terp.xx[i]); // 插值参数 t
        u = (x2p - x2terp.xx[j]) / (x2terp.xx[j+1] - x2terp.xx[j]); // 插值参数 u
        yy = (1.-t)*(1.-u)*y[i][j] + t*(1.-u)*y[i+1][j]
           + (1.-t)*u*y[i][j+1] + t*u*y[i+1][j+1];
        return yy;
    }
};

这里我们声明了两个 Linearinterp 实例，分别对应两个方向，仅用于对数组 $x_{1i}$ 和 $x_{2j}$ 进行簿记管理——特别是提供我们所依赖的“智能”查表机制。（构造函数中 x1v 和 x2v 的第二次出现只是一个占位符；实际上并不存在真正的一维“y”数组。）

Bilininterp 的使用方式正如你所预期的那样：

Int m = ..., n = ...;
MatDoub yy(m, n);
VecDoub x1(m), x2(n);
...
Bilininterp myfunc(x1, x2, yy);

随后（可多次）调用：

Doub x1, x2, y;
...
y = myfunc.interp(x1, x2);

除非你明确知道自己需要更复杂的方法，否则双线性插值是二维插值的一个良好起点。

在超越双线性插值、迈向更高阶方法时，主要有两个截然不同的方向：其一是使用更高阶方法以提高插值函数的精度（针对足够光滑的函数！），而不一定试图改善梯度及更高阶导数的连续性；其二是利用更高阶方法，在插值点跨越网格单元边界时，强制某些导数的光滑性。下面我们依次讨论这两个方向。

3.6.1 为提高精度而采用更高阶方法

基本思路是将问题分解为一系列一维插值。如果我们希望在 $x_1$ 方向上进行 $m-1$ 阶插值，在 $x_2$ 方向上进行 $n-1$ 阶插值，首先定位一个包含目标点 $(x_1,x_2)$ 的 $m\times n$ 子块。然后在该子块的每一行上进行 $m$ 次 $x_2$ 方向的一维插值，得到 $m$ 个点 $(x_{1i},x_2)$ 处的函数值。最后再在 $x_1$ 方向上进行一次插值，得到最终结果。

同样借助之前的一维插值机制，可以非常简洁地实现如下：

struct Poly2Dinterp {
    // 用于矩阵上的二维多项式插值的对象。
    // 构造时传入 x1 值的向量、x2 值的向量、制表函数值 y_{ij} 的矩阵，
    // 以及两个整数，用于指定在每个方向上局部使用的点数。
    // 然后调用 interp 获取插值结果。

    Int m, n, mn;
    const MatDoub &y;
    VecDoub yv;
    Polyinterp x1terp, x2terp;

    Poly2Dinterp(VecDoub_I &x1v, VecDoub_I &x2v, MatDoub_I &ym,

Int mp, Int np) : m(x1v.size()), n(x2v.size()),
mm(mp), nn(np), y(ym), yv(m),
x1terp(x1v,yv,mm), x2terp(x2v,x2v,nn) {}
// 用于其 locate 和 hunt 函数的虚拟一维插值。
Doub interp(Doub x1p, Doub x2p) {
    Int i,j,k;
    i = x1terp.cor ? x1terp.hunt(x1p) : x1terp.locate(x1p);
    j = x2terp.cor ? x2terp.hunt(x2p) : x2terp.locate(x2p);
    // 找到网格块。
    for (k=i; k<i+mm; k++) {
        x2terp.yy = &y[k][0];
        yv[k] = x2terp.rawinterp(j,x2p);
    }
    return x1terp.rawinterp(i,x1p);
}

用户接口与 Bilin_interp 相同，只是构造函数多了两个参数，分别指定在 $x_1$ 和 $x_2$ 插值中局部使用的点数（阶数加一）。典型值范围为 3 到 7。

代码风格主义者可能不喜欢 Poly2Dinterp 中的一些细节（参见 §3.1 中紧接 Base_interp 后的讨论）。当我们遍历子块的行时，我们直接深入 x2terp 的内部，将其 yy 数组重新指向我们的 y 矩阵的一行。此外，我们动态修改 yv 数组的内容，而 x1terp 已经存储了该数组的指针。只要我们同时控制 Base_interp 和 Poly2Dinterp 的实现，这些操作就并不特别危险；而且它能实现非常高效的代码。你应该将这两个类不仅视为（隐式的）友元类，而且视为非常亲密的朋友。

3.6.2 为光滑性而采用的高阶方法：双三次样条

在二维插值中获得光滑性的常用技术是双三次样条。要建立双三次样条，你（一次性）在函数值二维矩阵的各行上构造 $M$ 个一维样条。然后，对于每个所需的插值点，按如下步骤进行：(1) 执行 $M$ 次样条插值，得到向量值 $y(x_{1i},x_2)$，其中 $i=0,\dots ,M-1$。(2) 通过这些值构造一个一维样条。(3) 最后，对所需值 $y(x_1,x_2)$ 进行样条插值。

如果这听起来工作量很大，那确实如此。一次性设置的工作量与表格大小 $M\times N$ 成正比，而每次插值的工作量大致为 $M\log M+N$，且前面都有相当大的常数因子。这是为获得样条因其非局部性而具有的优良特性所必须付出的代价。对于 $M$ 和 $N$ 适中的表格（例如小于几百），这种代价通常是可接受的。如果不可接受，则退回到前面的局部方法。

同样，可以实现非常简洁的代码：

struct Spline2Dinterp {
    // 用于矩阵上的二维三次样条插值的对象。
    // 构造时传入 x1 值向量、x2 值向量和表格化函数值矩阵 y_{ij}。
    // 然后调用 interp 获取插值结果。
    Int m,n;
    const MatDoub &y;
    const VecDoub &x1;
    VecDoub yv;
    NRvector<Spline_interp*> srp;

    Spline2Dinterp(VecDoub_I &x1v, VecDoub_I &x2v, MatDoub_I &ym)
    : m(x1v.size()), n(x2v.size()), y(ym), yv(m), x1(x1v), srp(m) {
        for (Int i=0; i<m; i++) srp[i] = new Spline_interp(x2v, &y[i][0]);
        // 保存指向一维行样条的指针数组。
    }
    ~Spline2Dinterp() {
        for (Int i=0; i<m; i++) delete srp[i];
    } // 需要析构函数进行清理。
    Doub interp(Doub x1p, Doub x2p) {
        for (Int i=0; i<m; i++) yv[i] = (*srp[i]).interp(x2p);
        // 在每一行上插值。
        Spline_interp scol(x1, yv);
        return scol.interp(x1p);
    }
};

使用指向 Spline_interp 对象的指针向量的原因是，我们需要用相应行的数据分别初始化每个行样条。用户接口与上面的 Bilin_interp 相同。

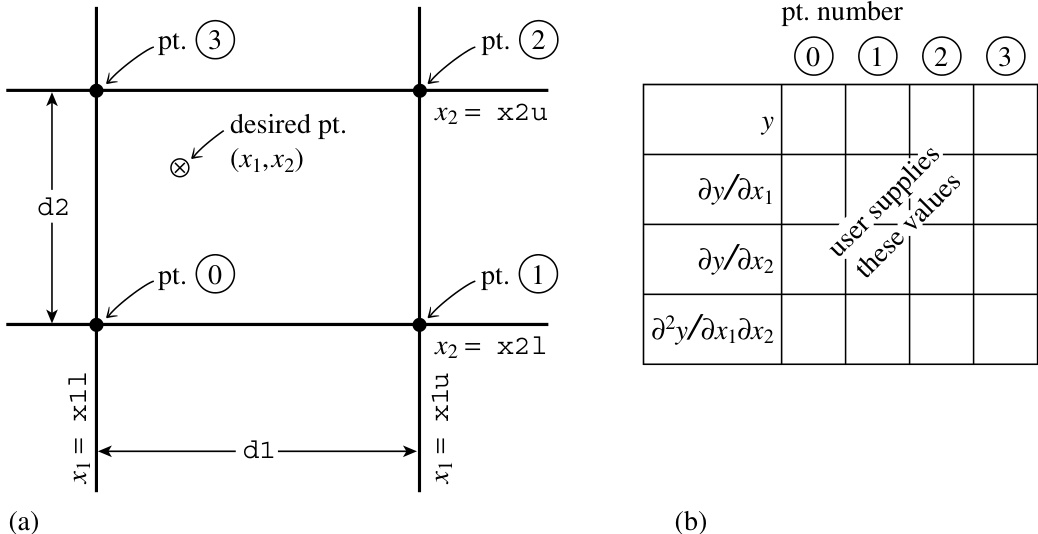
图 3.6.1. (a) 二维插值例程 bcuint 和 bcucof 中所用点的标记。(b) 对于 (a) 中的四个点，用户需提供一个函数值、两个一阶导数和一个混合导数，共 16 个数值。

3.6.3 为光滑性而采用的高阶方法：双三次插值

双三次插值提供了与双三次样条插值相同的光滑度，但它具有局部方法的优点。因此，在设置完成后，函数插值的代价仅为一个常数加上 $\log M+\log N$（用于在表格中定位）。不幸的是，这一优点带来了编码上的大量复杂性。在此，我们仅给出该方法的一些构建模块，而非完整的用户接口。

双三次样条实际上是双三次插值的一个特例。然而在一般情况下，我们将网格点上所有导数的值留作自由指定。你可以按任意方式指定它们。换句话说，在每个网格点上，你不仅指定函数 $y(x_1,x_2)$，还指定梯度 $\partial y/\partial x_1\equiv y_1$、$\partial y/\partial x_2\equiv y_2$ 以及混合导数 ${\partial }^{2}y/\partial x_1\partial x_2\equiv y_{12}$（见图 3.6.1）。然后可以找到一个在缩放坐标 $t$ 和 $u$（公式 3.6.4）下为三次的插值函数，具有以下性质：(i) 在网格点上精确重现函数值和指定的导数值；(ii) 当插值点从一个网格方块跨越到另一个时，函数值和指定的导数值连续变化。

重要的是要理解，双三次插值的方程并不要求你正确指定额外的导数！光滑性是“强制”实现的，与所指定导数的“准确性”无关。如何获得这些指定值是你需要单独解决的问题。你做得越好，插值就越准确。但无论你怎么做，插值结果都是光滑的。

最好的情况是在网格点上解析地知道导数，或能通过数值方法准确计算它们。次优的方法是通过已有的网格函数值进行数值差分来确定导数。相关代码可能如下所示（使用中心差分）：

$$\begin{array}{rl}& y1a[\mathrm{j}][\mathrm{k}]=(\mathrm{ya}[\mathrm{j}+1][\mathrm{k}]-\mathrm{ya}[\mathrm{j}-1][\mathrm{k}])/(x1a[\mathrm{j}+1]-x1a[\mathrm{j}-1]);\\ & y2a[\mathrm{j}][\mathrm{k}]=(\mathrm{ya}[\mathrm{j}][\mathrm{k}+1]-\mathrm{ya}[\mathrm{j}][\mathrm{k}-1])/(x2a[\mathrm{k}+1]-x2a[\mathrm{k}-1]);\\ & y12a[\mathrm{j}][\mathrm{k}]=(\mathrm{ya}[\mathrm{j}+1][\mathrm{k}+1]-\mathrm{ya}[\mathrm{j}+1][\mathrm{k}-1]-\mathrm{ya}[\mathrm{j}-1][\mathrm{k}+1]+\mathrm{ya}[\mathrm{j}-1][\mathrm{k}-1])\\ & /((x1a[\mathrm{j}+1]-x1a[\mathrm{j}-1])\ast (x2a[\mathrm{k}+1]-x2a[\mathrm{k}-1]));\end{array}$$

要在网格方块内进行双三次插值，给定方块四个角点处的函数值 $y$ 和导数 $y1$、$y2$、$y12$，分为两步：首先使用下面的 bcucof 例程计算 16 个量 $c_{ij}$（$i,j=0,\dots ,3$）。（从函数值和导数值计算 $c$ 的公式只是一个复杂的线性变换，其系数在数值计算历史的早期已被确定，可以制成表格后遗忘。）然后，根据需要将 $c$ 代入以下任意或全部双三次公式以计算函数值和导数值：

$$\begin{array}{rl}& y(x_1,x_2)=\sum _{i=0}^3\sum _{j=0}^3{c}_{ij}{t}^i{u}^j\\ & y_{,1}(x_1,x_2)=\sum _{i=0}^3\sum _{j=0}^{3}i{c}_{ij}{t}^{i-1}{u}^j(dt/d{x}_1)\\ & y_{,2}(x_1,x_2)=\sum _{i=0}^3\sum _{j=0}^{3}j{c}_{ij}{t}^i{u}^{j-1}(du/d{x}_2)\\ & y_{,12}(x_1,x_2)=\sum _{i=0}^3\sum _{j=0}^{3}ij{c}_{ij}{t}^{i-1}{u}^{j-1}(dt/d{x}_1)(du/d{x}_2)\end{array}$$

其中 $t$ 和 $u$ 仍由公式 (3.6.4) 给出。

void bcucof(VecDoub_I &y, VecDoub_I &y1, VecDoub_I &y2, VecDoub_I &y12,
            Doub d1, Doub d2, MatDoub_O &c)

给定数组 y[0..3]、y1[0..3]、y2[0..3] 和 y12[0..3]，其中包含矩形网格单元四个网格点（从左下角开始逆时针编号）处的函数值、梯度和混合导数，以及给定 d1 和 d2（网格单元在 1 和 2 方向的长度），该例程返回由 bcuint 例程用于双三次插值的表 c[0..3][0..3]。

static Int wt[16][16]=
{1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0};

VecDoub x(16), cl(16);
for (Int i=0; i<4; i++) {
    x[i]   = y[i];
    x[i+4] = y1[i]*d1;
    x[i+8] = y2[i]*d2;
    x[i+12]= y12[i]*d1*d2;
}
for (Int i=0; i<16; i++) {
    Doub xx=0.0;
    for (Int k=0; k<16; k++) xx += wt[i][k]*x[k];
    cl[i]=xx;
}
Int l=0;
for (Int i=0; i<4; i++) // 将结果解包到输出表中。
    for (Int j=0; j<4; j++) c[i][j]=cl[l++];
}

实现公式 (3.6.6) 的双三次插值例程，返回插值函数值和两个梯度值，并使用上述 bcucof 例程，其代码非常简单：

interp_2d.h

void bcuint(VecDoub_I &y, VecDoub_I &y1, VecDoub_I &y2, VecDoub_I &y12,
            const Doub x1l, const Doub x1u, const Doub x2l, const Doub x2u,
            const Doub x1, const Doub x2, Doub &ansy, Doub &ansy1, Doub &ansy2) {
    // 在网格单元内进行双三次插值。输入量包括 y, y1, y2, y12（如 bcucof 中所述）；
    // x1l 和 x1u 是网格单元在第 1 方向上的下界和上界坐标；
    // x2l 和 x2u 是第 2 方向上的对应坐标；
    // x1, x2 是待插值点的坐标。
    // 插值得到的函数值通过 ansy 返回，插值得到的梯度值通过 ansy1 和 ansy2 返回。
    // 本例程调用 bcucof。

    Int i;
    Doub t, u, d1 = x1u - x1l, d2 = x2u - x2l;
    MatDoub c(4, 4);
    bcucof(y, y1, y2, y12, d1, d2, c);
    if (x1u == x1l || x2u == x2l)
        throw("Bad input in routine bcuint");
    t = (x1 - x1l) / d1;
    u = (x2 - x2l) / d2;
    ansy = ansy2 = ansy1 = 0.0;
    for (i = 3; i >= 0; i--) {
        ansy = t * ansy + ((c[i][3] * u + c[i][2]) * u + c[i][1]) * u + c[i][0];
        ansy2 = t * ansy2 + (3.0 * c[i][3] * u + 2.0 * c[i][2]) * u + c[i][1];
        ansy1 = u * ansy1 + (3.0 * c[3][i] * t + 2.0 * c[2][i]) * t + c[1][i];
    }
    ansy1 /= d1;
    ansy2 /= d2;
}

你可以通过以下方式结合双三次插值和双三次样条的最佳特性：使用样条方法计算网格点处所需的导数值，将这些值存储起来，然后在实际函数插值时使用双三次插值，并配合高效的查表方法。不幸的是，这超出了我们此处的讨论范围。

参考文献

Abramowitz, M., and Stegun, I.A. 1964, Handbook of Mathematical Functions (Washington: National Bureau of Standards); 1968年重印版 (New York: Dover); 在线版本见 http://www.nr.com/aands, §25.2。

Johnson, L.W., and Riess, R.D. 1982, Numerical Analysis, 第2版 (Reading, MA: Addison-Wesley), §5.2.7。

Dahlquist, G., and Bjorck, A. 1974, Numerical Methods (Englewood Cliffs, NJ: Prentice-Hall); 2003年重印版 (New York: Dover), §7.7。

3.7 多维空间中散乱数据的插值

我们现在将（尽管有些忐忑地）离开规则网格的有序世界。这需要勇气。我们面对的是 $n$ 维空间中任意散乱分布的 $N$ 个数据点 $({\mathbf{x}}_i,y_i)$，其中 $i=0,\dots ,N-1$。这里 ${\mathbf{x}}_i$ 表示一个 $n$ 维自变量向量 $(x_{1i},x_{2i},\dots ,x_{ni})$，而 $y_i$ 是函数在该点处的值。

本节讨论解决该问题的两种最广泛使用的通用方法：径向基函数（RBF）插值和克里金（kriging）法。这两种方法计算代价都很高。具体而言，它们需要 $O(N^3)$ 的运算量来预处理一组数据点，之后每次插值则需要 $O(N)$ 的运算量。克里金法还能提供误差估计，但代价更高，每次插值需 $O(N^2)$ 的运算量。下文将讨论的谢泼德（Shepard）插值是 RBF 的一种变体，至少避免了 $O(N^3)$ 的初始计算量；否则，这些计算负担实际上将这些通用方法的有效性限制在 $N\lesssim 10^4$ 的范围内。因此，你有必要考虑是否还有其他可行方案。其中两种方案是：

• 如果维数 $n$ 不太大（通常指 $n=2$），且数据点分布相当密集，则可考虑三角剖分法（见 §21.6）。三角剖分是有限元方法的一个例子。这类方法通过构造某种几何规则性，并利用该结构获得优势。网格生成是与之密切相关的课题。

• 如果你的精度要求允许，可考虑将每个数据点移动到最近的规则笛卡尔网格点上，然后使用拉普拉斯插值法（§3.8）填充其余网格点。之后，即可使用 §3.6 中的方法在网格上进行插值。你需要在网格精细度（以减小移动点引入的误差）和拉普拉斯方法的计算时间之间进行权衡。

如果上述方案均不可行，且你也想不出其他替代方案，那么可以尝试下面将要讨论的两种方法之一或两者。RBF 插值可能是两者中应用更广泛的一种，但克里金法是我们个人的偏好。哪种方法效果更好，取决于你具体问题的细节。

本节末尾还将讨论一个相关但更简单的问题：多维空间中的曲线插值。

3.7.1 径向基函数插值

RBF 插值背后的思想非常简单：假设每个已知点 $j$ 以其周围相同的方式在所有方向上产生“影响”，这种影响遵循某个预设的函数形式 $\varphi (r)$ —— 即径向基函数 —— 它仅是到该点的径向距离 $r=|\mathbf{x}-{\mathbf{x}}_j|$ 的函数。我们尝试用所有已知点为中心的 $\varphi$ 函数的线性组合来近似整个插值函数：

$$y(\mathbf{x})=\sum _{i=0}^{N-1}{w}_i\varphi (|\mathbf{x}-{\mathbf{x}}_i|)$$

其中 $w_i$ 是一组未知的权重系数。如何确定这些权重？我们尚未使用函数值 $y_i$。权重的确定要求插值在所有已知数据点处精确成立。这等价于求解一个含 $N$ 个未知数 $w_i$ 的 $N$ 元线性方程组：

$$y_j=\sum _{i=0}^{N-1}{w}_i\varphi (|{\mathbf{x}}_j-{\mathbf{x}}_i|)$$

对于许多函数形式 $\varphi$，在各种一般性假设下，可以证明该方程组是非奇异的，并可通过例如 $LU$ 分解（§2.3）轻松求解。参考文献 [1,2] 提供了相关文献的入口。

RBF 插值的一种变体是归一化径向基函数（NRBF）插值，它要求基函数之和为 1，或者等价地，将方程 (3.7.1) 和 (3.7.2) 替换为：

$$y(\mathbf{x})=\frac{{\sum }_{i=0}^{N-1}{w}_i\varphi (|\mathbf{x}-{\mathbf{x}}_i|)}{{\sum }_{i=0}^{N-1}\varphi (|\mathbf{x}-{\mathbf{x}}_i|)}$$

和

$$y_j\sum _{i=0}^{N-1}\varphi (|{\mathbf{x}}_j-{\mathbf{x}}_i|)=\sum _{i=0}^{N-1}{w}_i\varphi (|{\mathbf{x}}_j-{\mathbf{x}}_i|)$$

方程 (3.7.3) 和 (3.7.4) 更自然地源于贝叶斯统计视角 [3]。然而，并无证据表明 NRBF 方法始终优于 RBF 方法，反之亦然。在同一个代码中同时实现这两种方法很容易，可将选择权留给用户。

如前所述，对于 $N$ 个数据点，通过 $LU$ 分解一次性求解权重的计算量为 $O(N^3)$。此后，每次插值的代价为 $O(N)$。因此，在 2007 年的桌面计算机速度下，$N\sim 10^3$ 大致是“容易”与“困难”的分界线。然而，如果你的 $N$ 更大，也无需绝望：存在快速多极子方法（fast multipole methods），其计算复杂度更有利 [1,4,5]，但这超出了本文的讨论范围。另一种技术含量低得多的选择是使用本节稍后讨论的谢泼德插值。

以下是实现上述所有内容的两个类。RBF_fn 是一个虚基类，其派生类将实现不同的径向基函数形式 rbf($r$) $\equiv$ $\varphi (r)$。RBFinterp 类通过其构造函数处理你的数据并求解权重方程。数据点 ${\mathbf{x}}_i$ 以 $N\times n$ 矩阵形式输入，代码适用于任意维度 $n$。布尔参数 nrbf 指定是否使用 NRBF 而非 RBF。调用 interp 方法即可在新点 $\mathbf{x}$ 处获得插值函数值。

struct RBF_fn {
    // 任意特定径向基函数的抽象基类模板。参见下面的具体示例。
    virtual Doub rbf(Doub r) = 0;
};

struct RBFinterp {
    // 使用 dim 维空间中 n 个点进行径向基函数插值的对象。
    // 构造函数调用一次，之后可多次调用 interp。
    Int dim, n;
    const MatDoub &pts;
    const VecDoub &vals;
    VecDoub w;
    RBF_fn &fn;
    Bool norm;

    RBFinterp(MatDoub_I &ptss, VecDoub_I &valss, RBF_fn &func, Bool nrbf = false)
        : dim(ptss.ncols()), n(ptss.nrows()), pts(ptss), vals(valss),
          w(n), fn(func), norm(nrbf) {
        // 构造函数。n × dim 矩阵 ptss 输入数据点，向量 valss 输入函数值。
        // func 包含从 RBF_fn 类派生的选定径向基函数。
        // nrbf 的默认值给出 RBF 插值；设为 true 则使用归一化 RBF (NRBF)。

        Int i, j;
        Doub sum;
        MatDoub rbf(n, n);
        VecDoub rhs(n);
        for (i = 0; i < n; i++) {
            sum = 0.;
            for (j = 0; j < n; j++) {
                sum += (rbf[i][j] = fn.rbf(rad(&pts[i][0], &pts[j][0])));
            }
            if (norm) rhs[i] = sum * vals[i];
            else rhs[i] = vals[i];
        }
        LUDcmp lu(rbf);
        lu.solve(rhs, w);
    }

    Doub interp(VecDoub_I &pt) {
        // 返回在 dim 维点 pt 处的插值函数值。
        Doub fval, sum = 0., sumw = 0;
        if (pt.size() != dim) throw("RBFinterp bad pt size");
        for (Int i = 0; i < n; i++) { // 对所有表格点求和。
            fval = fn.rbf(rad(&pt[0], &pts[i][0]));
            sumw += w[i] * fval;
            sum += fval;
        }
        return norm ? sumw / sum : sumw;
    }
};

Doub rad(const Doub *p1, const Doub *p2) {
    // 欧几里得距离。
    Doub sum = 0;
    for (Int i = 0; i < dim; i++) sum += SQR(p1[i] - p2[i]);
    return sqrt(sum);
}

3.7.2 常用的径向基函数

最常用的径向基函数是 Hardy 于 1970 年左右首次使用的 多元二次函数（multiquadric）。其函数形式为：

$$\varphi (r)=(r^2+r_0^2{)}^{1/2}$$

其中 $r_0$ 是一个可自行选择的尺度因子。据说多元二次函数对 $r_0$ 的选择不如其他一些函数形式敏感。

一般而言，无论是多元二次函数还是下面提到的其他函数，$r_0$ 应大于数据点的典型间距，但小于所插值函数的“外尺度”或特征尺度。选择合适的 $r_0$ 与选择不当相比，插值精度可能相差几个数量级，因此值得进行一些实验。一种实验方法是每次省略一个数据点构造 RBF 插值器，并测量在被省略点处的插值误差。

逆多元二次函数（inverse multiquadric）：

$$\varphi (r)=(r^2+r_0^2{)}^{-1/2}$$

其结果与多元二次函数相当，有时甚至更好。

一个函数与其倒数（实际上是倒数）效果相近，这看起来可能有些奇怪。其解释在于真正重要的是函数的光滑性，以及其傅里叶变换的某些性质——这些性质在多元二次函数与其倒数之间差别不大。一个函数单调递增而另一个单调递减的事实几乎无关紧要。然而，如果你希望外推函数在远离所有数据点处趋于零（在那里无论如何也无法获得准确值），那么逆多元二次函数是一个不错的选择。

薄板样条（thin-plate spline）径向基函数为：

$$\varphi (r)=r^2\log (r/r_0)$$

并约定极限值 $\varphi (0)=0$。该函数在与薄弹性板弯曲相关的能量最小化问题中有一定的物理依据。然而，并没有证据表明它普遍优于上述任一形式。

高斯径向基函数（Gaussian radial basis function）正如你所预期：

$$\varphi (r)=\exp \left(-\frac{1}{2}{r}^2/r_0^2\right)$$

使用高斯基函数进行插值时，精度对 $r_0$ 非常敏感，因此常因这一原因而被避免使用。然而，对于光滑函数并在最优 $r_0$ 下，可以达到非常高的精度。高斯函数还会将任何函数在外推时快速趋于零。

其他函数也在使用中，例如 Wendland 的函数 [6]。大量文献对上述基函数选择与特定函数形式或实验数据集进行了测试 [1,2,7]。但几乎没有（如果有的话）普适性的推荐结论。我们建议你按上述顺序尝试各种选项，从多元二次函数开始，并且不要忽略对尺度参数 $r_0$ 的不同选择进行实验。

上述讨论的函数在代码中实现如下：

struct RBF_multiquadric : RBF_fn {
    // 实例化此结构体并传给 RBFinterp 以进行多元二次插值。
    Doub r02;
    RBF_multiquadric(Doub scale = 1.) : r02(SQR(scale)) {}
    // 构造函数参数为尺度因子。参见正文。
    Doub rbf(Doub r) { return sqrt(SQR(r) + r02); }
};

struct RBF_thinplate : RBF_fn {
    // 同上，但用于薄板样条。
    Doub r0;
    RBF_thinplate(Doub scale = 1.) : r0(scale) {}
    Doub rbf(Doub r) { return r <= 0. ? 0. : SQR(r) * log(r / r0); }
};

struct RBF_gauss : RBF_fn {
    // 同上，但用于高斯函数。
    Doub r0;
    RBF_gauss(Doub scale = 1.) : r0(scale) {}
    Doub rbf(Doub r) { return exp(-0.5 * SQR(r / r0)); }
};

struct RBF_inversemultiquadric : RBF_fn {
    // 同上，但用于逆多元二次函数。
    Doub r02;
    RBF_inversemultiquadric(Doub scale = 1.) : r02(SQR(scale)) {}
    Doub rbf(Doub r) { return 1. / sqrt(SQR(r) + r02); }
};

本节中对象的典型用法大致如下所示：

3.7.3 Shepard 插值

归一化径向基函数插值（公式 3.7.3 和 3.7.4）的一个有趣特例是：当函数 $\varphi (r)$ 在 $r\to 0$ 时趋于无穷大，而在 $r>0$ 时为有限值（例如单调递减）。在这种情况下，很容易看出权重 $w_i$ 恰好等于相应的函数值 $y_i$，插值公式简化为：

$$y(\mathbf{x})=\frac{{\sum }_{i=0}^{N-1}{y}_i\varphi (|\mathbf{x}-{\mathbf{x}}_i|)}{{\sum }_{i=0}^{N-1}\varphi (|\mathbf{x}-{\mathbf{x}}_i|)}$$

（需对 $\mathbf{x}$ 恰好等于某个 ${\mathbf{x}}_i$ 的极限情况进行适当处理）。注意，这里不需要求解线性方程组。一次性计算工作量可忽略不计，而每次插值的工作量为 $O(N)$，即使对于非常大的 $N$ 也是可接受的。

Shepard 提出了简单的幂律函数

$$\varphi (r)=r^{-p}$$

其中（通常）$1<p\lesssim 3$，以及一些更复杂的函数，其在内层和外层区域使用不同的指数（参见 [8]）。可以看出，其基本思想是通过一种基于邻近度加权的平均进行插值，邻近点的贡献比远处点更强。

Shepard 插值通常不如上述其他径向基函数经过良好调优后的应用那样精确。但另一方面，它简单、快速，常常非常适合用于快速而粗糙的应用场景。因此，它及其变体被广泛使用。

其实现对象如下：

struct Shepinterp {
    // 用于在 dim 维空间中使用 n 个点进行 Shepard 插值的对象。
    // 构造函数调用一次，之后可多次调用 interp。
    Int dim, n;
    const MatDoub &pts;
    const VecDoub &vals;
    Doub pneg;

    Shepinterp(MatDoub_I &ptss, VecDoub_I &valss, Doub p=2.)
        : dim(ptss.ncols()), n(ptss.nrows()), pts(ptss),
          vals(valss), pneg(-p) {}
    // 构造函数。n × dim 矩阵 ptss 输入数据点，向量 valss 输入函数值。
    // 设置 p 为所需的指数，默认值是典型值。

    Doub interp(VecDoub_I &pt) {
        // 返回 dim 维点 pt 处的插值函数值。
        Doub r, w, sum=0., sumw=0.;
        if (pt.size() != dim) throw("RBF.interp bad pt size");
        for (Int i=0; i<n; i++) {
            if ((r=rad(&pt[0], &pts[i][0])) == 0.) return vals[i];
            sum += (w = pow(r, pneg));
            sumw += w * vals[i];
        }
        return sumw / sum;
    }

    Doub rad(const Doub *p1, const Doub *p2) {
        // 欧几里得距离。
        Doub sum = 0.;
        for (Int i=0; i<dim; i++) sum += SQR(p1[i] - p2[i]);
        return sqrt(sum);
    }
};

3.7.4 克里金插值（Kriging）

克里金（Kriging）是一种以南非采矿工程师 D.G. Krige 命名的技术。它本质上是一种线性预测方法（参见 §13.6），在不同领域也被称为高斯-马尔可夫估计或高斯过程回归。

克里金既可以作为插值方法，也可以作为拟合方法。两者的区别在于：拟合/插值函数是否精确通过所有输入数据点（插值），或者是否允许指定测量误差，从而进行“平滑”以获得统计上更优的预测器，该预测器通常不通过数据点（即不“忠实于数据”）。本节仅考虑前者，即插值情形。我们将在 §15.9 中讨论后者。

在本书的这一阶段，推导克里金方程已超出我们的范围。你可以参考 §13.6 以了解其大致思想，并查阅文献 [9,10,11] 获取详细内容。要使用克里金方法，你必须能够估计函数 $y(\mathbf{x})$ 的均方变化量作为偏移距离 $\mathbf{r}$ 的函数，即所谓的变差函数（variogram）：

$$\begin{array}{r}v(\mathbf{r})\sim \frac{1}{2}⟨[y(\mathbf{x}+\mathbf{r})-y(\mathbf{x}){]}^2⟩\end{array}$$

其中平均是对所有固定 $\mathbf{r}$ 的 $\mathbf{x}$ 进行的。如果这看起来令人望而生畏，不必担心。对于插值而言，即使是非常粗糙的变差函数估计也足够有效。下面我们将给出一个例程，可自动根据你的输入数据点 ${\mathbf{x}}_i$ 和 $y_i=y({\mathbf{x}}_i)$（$i=0,\dots ,N-1$）来估计 $v(\mathbf{r})$。通常假设 $v(\mathbf{r})$ 仅是模长 $r=|\mathbf{r}|$ 的函数，并记作 $v(r)$。

令 $v_{ij}$ 表示 $v(|{\mathbf{x}}_i-{\mathbf{x}}_j|)$，其中 $i$ 和 $j$ 为输入点；令 $v_{\ast j}$ 表示 $v(|{\mathbf{x}}_{\ast }-{\mathbf{x}}_j|)$，其中 ${\mathbf{x}}_{\ast }$ 是我们希望插值得到 $y({\mathbf{x}}_{\ast })$ 的点。现在定义两个长度为 $N+1$ 的向量：

$$\begin{array}{r}\mathbf{Y}=(y_0,y_1,\dots ,y_{N-1},0)\\ {\mathbf{V}}_{\ast }=(v_{\ast 0},v_{\ast 1},\dots ,v_{\ast ,N-1},1)\end{array}$$

以及一个 $(N+1)\times (N+1)$ 的对称矩阵：

$$\mathbf{V}=\left(\begin{array}{lllll}{v}_{00}& v_{01}& \dots & v_{0,N-1}& 1\\ v_{10}& v_{11}& \dots & v_{1,N-1}& 1\\ ⋮& ⋮& \dots & ⋮& ⋮\\ v_{N-1,0}& v_{N-1,1}& \dots & v_{N-1,N-1}& 1\\ 1& 1& \dots & 1& 0\end{array}\right)$$

则克里金插值估计值 ${\hat{y}}_{\ast }\approx y({\mathbf{x}}_{\ast })$ 由下式给出：

$${\hat{y}}_{\ast }={\mathbf{V}}_{\ast }\cdot {\mathbf{V}}^{-1}\cdot \mathbf{Y}$$

其方差为：

$$\mathrm{Var}({\hat{y}}_{\ast })={\mathbf{V}}_{\ast }\cdot {\mathbf{V}}^{-1}\cdot {\mathbf{V}}_{\ast }$$

注意，如果我们一次性计算出 $\mathbf{V}$ 的 $LU$ 分解，然后回代一次得到向量 ${\mathbf{V}}^{-1}\cdot \mathbf{Y}$，那么每次单独插值的计算代价仅为 $O(N)$：只需计算向量 ${\mathbf{V}}_{\ast }$ 并进行点积运算。然而，每次计算方差（公式 (3.7.15)）都需要一次 $O(N^2)$ 的回代运算。

顺便提一下（如果你已提前阅读 §13.6），矩阵 $\mathbf{V}$ 中额外的一行一列，以及 ${\mathbf{V}}_{\ast }$ 和 $\mathbf{Y}$ 中额外的最后一个分量，其目的是自动计算并校正数据的适当加权平均值，从而使公式 (3.7.14) 成为一个无偏估计量。

以下是公式 (3.7.12) – (3.7.15) 的实现。构造函数完成一次性计算工作，而两个重载的 interp 方法分别计算插值结果，或同时计算插值结果及其标准差（方差的平方根）。在阅读 §15.9 之前，应将可选参数 err 保持为默认的 NULL 值。

template<class T>
struct Krig {
    // 用于在 ndim 维空间中使用 npt 个点进行克里金插值的对象。
    // 构造函数调用一次，之后可多次调用 interp。
    const MatDoub &x;
    const T &vgram;
    Int ndim, npt;
    Doub lastval, lasterr;
    VecDoub y, dstar, vstar, yvi;
    MatDoub v;
    LUdcmp *vi;

    Krig(MatDoub_I &xx, VecDoub_I &yy, T &vargram, const Doub *err=NULL)
        : x(xx), vgram(vargram), npt(xx.nrows()), ndim(xx.ncols()),
          dstar(npt+1), vstar(npt+1), v(npt+1, npt+1), y(npt+1), yvi(npt+1) {
        // 构造函数。npt × ndim 矩阵 xx 输入数据点，向量 yy 输入函数值。
        // vargram 是变差函数或函数对象。
        // 参数 err 在插值中未使用；参见 §15.9。

        Int i, j;
        for (i = 0; i < npt; i++) {
            y[i] = yy[i];
            for (j = i; j < npt; j++) {
                v[i][j] = v[j][i] = vgram(rdist(&x[i][0], &x[j][0]));
            }
            v[i][npt] = v[npt][i] = 1.;
        }
        v[npt][npt] = y[npt] = 0.;
    }
};
if (err) for (i=0;i<npt;i++) v[i][i] = SQR(err[i]); // $15.9.
vi = new LUdcmp(v);
vi->solve(y,yvi);
}
~Krig() { delete vi; }
Doub interp(VecDoub_I &xstar) {
    // 在点 xstar 处返回插值结果。
    Int i;
    for (i=0;i<npt;i++) vstar[i] = vgram(rdist(&xstar[0],&x[i][0]));
    vstar[npt] = 1.;
    lastval = 0.;
    for (i=0;i<=npt;i++) lastval += yvi[i]*vstar[i];
    return lastval;
}

Doub interp(VecDoub_I &xstar, Doub &esterr) {
    // 在点 xstar 处返回插值结果，并通过 esterr 返回其估计误差。
    lastval = interp(xstar);
    vi->solve(vstar,dstar);
    lasterr = 0;
    for (Int i=0;i<=npt;i++) lasterr += dstar[i]*vstar[i];
    esterr = lasterr = sqrt(MAX(0.,lasterr));
    return lastval;
}

Doub rdist(const Doub *x1, const Doub *x2) {
    // 内部使用的工具函数：计算两点间的欧氏距离。
    Doub d=0;
    for (Int i=0;i<ndim;i++) d += SQR(x1[i]-x2[i]);
    return sqrt(d);
};

构造函数参数 vgram（变差函数）可以是一个函数或函数对象（functor）（§1.3.3）。对于插值，你可以使用一个 Powvargram 对象，它拟合一个简单模型：

$$\nu (r)=\alpha r^{\beta }$$

其中 $\beta$ 被视为固定值，而 $\alpha$ 通过对所有数据点对 $i$ 和 $j$ 进行无权重最小二乘拟合得到。我们将在 §15.9 中更深入地讨论变差函数；但对于插值而言，这种简单选择通常能获得极佳的结果。$\beta$ 的取值应在区间 $1\le \beta <2$ 内。一个通用的良好选择是 1.5，但对于具有强线性趋势的函数，你可能需要尝试接近 1.99 的值。（$\beta =2$ 会导致矩阵退化并产生无意义的结果。）可选参数 nug 将在 §15.9 中解释。

struct Powvargram {
    // 变差函数 $v(r)=\alpha r^{\beta}$ 的函数对象，其中 $\beta$ 由用户指定，$\alpha$ 由数据拟合得到。
    Doub alpha, bet, nugsq;

    Powvargram(MatDoub_I &x, VecDoub_I &y, const Doub beta=1.5, const Doub nug=0.)
    : bet(beta), nugsq(nug*nug) {
        // 构造函数。npt × ndim 矩阵 x 输入数据点，向量 y 输入函数值，beta 指定 $\beta$ 值。
        // 对于插值，默认的 beta 值通常已足够。关于（罕见的）nug 的用法，参见 §15.9。
        Int i,j,k,npt=x.nrows(),ndim=x.ncols();
        Doub rb, num=0, denom=0;
        for (i=0;i<npt;i++) for (j=i+1;j<npt;j++) {
            rb = 0.;
            for (k=0;k<ndim;k++) rb += SQR(x[i][k]-x[j][k]);
            rb = pow(rb, bet);
            num += rb*(0.5*SQR(y[i]-y[j]) - nugsq);
            denom += SQR(rb);
        }
        alpha = num/denom;
    }
    Doub operator() (const Doub r) const {return nugsq+alpha*pow(r,bet);}
};

对一组数据点进行插值的示例代码如下：

随后可进行任意次数的插值调用，形式为：

ystar = krig.interp(xstar);

需要注意的是，虽然插值结果对变差函数模型不太敏感，但估计的误差却相当敏感。因此，你应仅将误差估计视为数量级意义上的参考。此外，由于计算误差估计的代价相对较高，因此在此类应用中其价值并不大。但在 §15.9 中，当我们的模型包含测量误差时，这些误差估计将变得更有用。

3.7.5 多维空间中的曲线插值

另一种值得简要提及的插值类型是：当你有一组按顺序排列的 $N$ 个 $n$ 维表格点 ${\mathbf{x}}_0,\dots ,{\mathbf{x}}_{N-1}$，它们位于一条一维曲线上，并希望沿该曲线插值得到其他点的值。值得区分的两种情形是：(i) 曲线为开曲线，即 ${\mathbf{x}}_0$ 和 ${\mathbf{x}}_{N-1}$ 为端点；(ii) 曲线为闭曲线，即隐含存在一条从 ${\mathbf{x}}_{N-1}$ 回到 ${\mathbf{x}}_0$ 的曲线段。

一个直接的解决方案（利用已有方法）是：首先用表格点之间的弦长之和近似曲线上的弧长，然后以该参数为自变量，对每个坐标分量 $0,\dots ,n-1$ 分别构造样条插值。由于任一坐标分量对弧长的导数绝对值不超过 1，因此可保证样条插值行为良好。

大约 90% 的应用场景只需上述方法即可。如果你不幸属于剩下的 10%，则需要学习贝塞尔曲线、B 样条以及更一般的插值样条 [12,13,14]。对于大多数幸运用户，其实现如下：

struct Curveinterp {
    // 用于插值由 n 个 dim 维点定义的曲线的对象。
    Int dim, n, in;
    Bool cls;
    MatDoub pts;
    VecDoub s;
    VecDoub ans;
    NRvector<Splineinterp*> srp;

    Curveinterp(MatDoub &ptsin, Bool close=0)
    : n(ptsin.nrows()), dim(ptsin.ncols()), in(close ? 2*n : n),
      cls(close), pts(dim,in), s(in), ans(dim), srp(dim) {
        // 构造函数。n × dim 矩阵 ptsin 输入数据点。
        // close 为 0 表示开曲线，1 表示闭曲线。
        // （对于闭曲线，最后一个数据点不应与第一个重复——算法会自动连接它们。）

        Int i,ii,im,j,ofs;
        Doub ss,soff,db,de;
        ofs = close ? n/2 : 0;
        s[0] = 0.;
        for (i=0;i<in;i++) {
            ii = (i-ofs+n) % n;
            im = (ii-1+n) % n;
            for (j=0;j<dim;j++) pts[j][i] = ptsin[ii][j];
            if (i>0) {
                // 累积弧长。
                s[i] = s[i-1] + rad(&ptsin[ii][0],&ptsin[im][0]);
                if (s[i] == s[i-1]) throw("error in Curveinterp");
                // 连续点不能相同。对于闭曲线，最后一个数据点不应与第一个重复。
            }
        }
        ss = close ? s[ofs+n]-s[ofs] : s[n-1]-s[0];
        soff = s[ofs];
        // 重缩放参数，使得截断点 = s[ofs];
        for (i=0;i<in;i++) s[i] = (s[i]-soff)/ss;
        for (j=0;j<dim;j++) {
            db = in < 4 ? 1.e99 : fprime(&s[0],&pts[j][0],1);
            de = in < 4 ? 1.e99 : fprime(&s[in-1],&pts[j][in-1],-1);
            srp[j] = new Splineinterp(s, &pts[j][0], db, de);
        }
    }
    ~Curveinterp() {for (Int j=0;j<dim;j++) delete srp[j];}

    VecDoub &interp(Doub t) {
        // 在存储的曲线上插值一个点。该点由参数 t ∈ [0,1] 参数化。
        // 对于开曲线，t 超出此范围将返回外推值（危险！）。
        // 对于闭曲线，t 以 1 为周期。
        if (cls) t = t - floor(t);
        for (Int j=0;j<dim;j++) ans[j] = (*srp[j]).interp(t);
        return ans;
    }

    Doub fprime(Doub *x, Doub *y, Int pm) {
        // 用于估计端点处导数的工具函数。
        // x 和 y 指向端点的横坐标和纵坐标。
        // 若 pm 为 +1，则使用右侧点（左端点）；
        // 若 pm 为 -1，则使用左侧点（右端点）。见下文说明。
        Doub s1 = x[0]-x[pm*1], s2 = x[0]-x[pm*2], s3 = x[0]-x[pm*3],
             s12 = s1-s2, s13 = s1-s3, s23 = s2-s3;
        return -(s1*s2/(s13*s23*s3))*y[pm*3] + (s1*s3/(s12*s2*s23))*y[pm*2]
               -(s2*s3/(s1*s12*s13))*y[pm*1] + (1./s1+1./s2+1./s3)*y[0];
    }

    Doub rad(const Doub *p1, const Doub *p2) {
        // 欧氏距离。
        Doub sum = 0.;
        for (Int i=0;i<dim;i++) sum += SQR(p1[i]-p2[i]);
        return sqrt(sum);
    }
};

工具函数 fprime 利用四个连续的表格点 $(x_0,y_0),\dots ,(x_3,y_3)$ 估计函数在横坐标 $x_0$ 处的导数。该公式的推导可通过幂级数展开轻松完成：

$$y_0^{\prime }=-C_0{y}_0+C_1{y}_1-C_2{y}_2+C_3{y}_3$$

其中

$$\begin{array}{rl}& C_0=\frac{1}{s_1}+\frac{1}{s_2}+\frac{1}{s_3}\\ & C_1=\frac{s_2{s}_3}{s_1(s_2-s_1)(s_3-s_1)}\\ & C_2=\frac{s_1{s}_3}{(s_2-s_1)s_2(s_3-s_2)}\\ & C_3=\frac{s_1{s}_2}{(s_3-s_1)(s_3-s_2)s_3}\end{array}$$

其中

$$\begin{array}{rl}& s_1\equiv x_1-x_0\\ & s_2\equiv x_2-x_0\\ & s_3\equiv x_3-x_0\end{array}$$

参考文献

Buhmann, M.D. 2003, Radial Basis Functions: Theory and Implementations (Cambridge, UK: Cambridge University Press).[1]

Powell, M.J.D. 1992, "The Theory of Radial Basis Function Approximation" in Advances in Numerical Analysis II: Wavelets, Subdivision Algorithms and Radial Functions, ed. W. A. Light (Oxford: Oxford University Press), pp. 105–210.[2]

Wikipedia. 2007+, "Radial Basis Functions," at http://en.wikipedia.org.[3]

Beatson, R.K. and Greengard, L. 1997, "A Short Course on Fast Multipole Methods", in Wavelets, Multilevel Methods and Elliptic PDEs, eds. M. Ainsworth, J. Levesley, W. Light, and M. Marletta (Oxford: Oxford University Press), pp. 1–37.[4]

Beatson, R.K. and Newsam, G.N. 1998, "Fast Evaluation of Radial Basis Functions: Moment-Based Methods" in SIAM Journal on Scientific Computing, vol. 19, pp. 1428-1449.[5]

Wendland, H. 2005, Scattered Data Approximation (Cambridge, UK: Cambridge University Press).[6]

Franke, R. 1982, "Scattered Data Interpolation: Tests of Some Methods," Mathematics of Computation, vol. 38, pp. 181–200.[7]

Shepard, D. 1968, "A Two-dimensional Interpolation Function for Irregularly-spaced Data," in Proceedings of the 1968 23rd ACM National Conference (New York: ACM Press), pp. 517–524.[8]

Cressie, N. 1991, Statistics for Spatial Data (New York: Wiley).[9]

Wackernagel, H. 1998, Multivariate Geostatistics, 2nd ed. (Berlin: Springer).[10]

Rybicki, G.B., and Press, W.H. 1992, "Interpolation, Realization, and Reconstruction of Noisy, Irregularly Sampled Data," Astrophysical Journal, vol. 398, pp. 169–176.[11]

Isaaks, E.H., and Srivastava, R.M. 1989, Applied Geostatistics (New York: Oxford University Press).

Deutsch, C.V., and Journel, A.G. 1992, GSLIB: Geostatistical Software Library and User's Guide (New York: Oxford University Press).

Knott, G.D. 1999, Interpolating Cubic Splines (Boston: Birkhäuser).[12]

De Boor, C. 2001, A Practical Guide to Splines (Berlin: Springer).[13]

Prautzsch, H., Boehm, W., and Paluszny, M. 2002, Bézier and B-Spline Techniques (Berlin: Springer).[14]

3.8 拉普拉斯插值

本节讨论一个缺失数据或网格化问题，即如何在规则网格上恢复缺失或未测量的值。显然，我们需要从非缺失值进行某种形式的插值，但如何以一种有原则的方式来实现呢？

一种很好的方法是拉普拉斯插值（Laplace interpolation），有时也称为拉普拉斯/泊松插值（Laplace/Poisson interpolation），这种方法早在计算机时代初期就已被使用[1,2]。其基本思想是寻找一个插值函数 $y$ ，使其在无数据区域满足 $n$ 维拉普拉斯方程：

$${\nabla }^{2}y=0$$

而在所有已测数据点处满足：

$$y({\mathbf{x}}_i)=y_i$$

通常，这样的函数是存在的。之所以选择拉普拉斯方程（在所有可能的偏微分方程中），是因为拉普拉斯方程的解在某种意义上选择了最平滑的插值函数。具体而言，其解使梯度平方的积分最小化：

$${\int }_{\Omega }|\nabla y{|}^{2}d\Omega$$

其中 $\Omega$ 表示所关注的 $n$ 维区域。这是一个非常通用的思想，既适用于非规则网格，也适用于规则网格。然而，此处我们仅考虑后者。

为便于说明（也因为这是最有用的例子），我们进一步限定为二维情形，并考虑笛卡尔网格，其中 $x_1$ 和 $x_2$ 的取值均匀分布——就像棋盘一样。

在此几何结构下，拉普拉斯方程的有限差分近似具有特别简单的形式，该形式呼应了拉普拉斯方程连续解的中值定理：在任意自由网格点（即非测量点）处的解值等于其四个笛卡尔相邻点的平均值。（参见 §20.0。）事实上，这听起来已经非常像插值了。

如果 $y_0$ 表示某自由点处的值，而 $y_u$、$y_d$、$y_l$ 和 $y_r$ 分别表示其上、下、左、右相邻点处的值，则满足如下方程：

$$y_0-\frac{1}{\alpha }{y}_u-\frac{1}{\alpha }{y}_d-\frac{1}{\alpha }{y}_l-\frac{1}{\alpha }{y}_r=0$$

另一方面，对于具有测量值的网格点，则满足一个不同的（简单的）方程：

$$y_0=y_{0(\mathrm{measured})}$$

注意，这些非零的右端项使得线性方程组成为非齐次的，因此通常可解。

我们尚未完全完成，因为必须为上、下、左、右边界以及四个角点提供特殊形式的方程。体现“自然”边界条件（即没有预设的函数值偏好）的齐次选择如下：

$$\begin{array}{rl}{y}_0-\frac{1}{2}{y}_u-\frac{1}{2}{y}_d=0& (\mathrm{left}\mathrm{and}\mathrm{right}\mathrm{boundaries})\\ y_0-\frac{1}{2}{y}_l-\frac{1}{2}{y}_r=0& (\mathrm{top}\mathrm{and}\mathrm{bottom}\mathrm{boundaries})\\ y_0-\frac{1}{2}{y}_r-\frac{1}{2}{y}_d=0& (\mathrm{top}-\mathrm{left}\mathrm{corner})\\ y_0-\frac{1}{2}{y}_l-\frac{1}{2}{y}_u=0& (\mathrm{bottom}-\mathrm{left}\mathrm{corner})\\ y_0-\frac{1}{2}{y}_l-\frac{1}{2}{y}_d=0& (\mathrm{bottom}-\mathrm{right}\mathrm{corner})\end{array}$$

由于每个网格点恰好对应方程 (3.8.4)、(3.8.5) 或 (3.8.6) 中的一个，因此方程的数量与未知数的数量完全相等。若网格大小为 $M\times N$，则各有 $MN$ 个方程和未知数。这个数量可能相当大；但这些方程显然是高度稀疏的。我们通过从 §2.7 中的 Linbcg 基类派生一个子类来求解它们。在下面的 atimes 代码中，你可以很容易地识别出方程 (3.8.4)–(3.8.6) 的所有情形。

struct Laplaceinterp : Linbcg {
    // 通过求解拉普拉斯方程来插值矩阵中缺失数据的对象。
    // 构造函数调用一次，然后可求解一次或多次（参见正文）。
    MatDoub &mat;
    Int ii, jj;
    Int nn, iter;
    VecDoub b, y, mask;

    Laplaceinterp(MatDoub_IO &matrix) : mat(matrix), ii(mat.nrows()), jj(mat.ncols()), 
                                        nn(ii * jj), iter(0), b(nn), y(nn), mask(nn) {
        // 构造函数。输入矩阵 mat 中大于 1.e99 的值被视为缺失数据。
        // 在调用 solve 之前，矩阵不会被修改。
        Int i, j, k;
        Doub v1 = 0.;
        for (k = 0, i = 0; i < ii; i++)
            for (j = 0; j < jj; j++, k++) {
                if (mat[i][j] > 1.e99) {
                    mask[k] = 0;
                } else {
                    mask[k] = 1;
                    b[k] = mat[i][j];
                }
            }
    }

    Doub solve(const Doub tol = 1.e-6, const Int itmax = 0) {
        // 用适当的参数调用 Linbcg::solve。
        // 默认参数通常有效，此时本例程只需调用一次。
        // 原始矩阵 mat 将被插值解重新填充。
        Int i, j, k;
        Doub err;
        if (itmax <= 0) itmax = 2 * MAX(ii, jj);
        Linbcg::solve(b, y, 1, tol, itmax, iter, err);
        for (k = 0, i = 0; i < ii; i++)
            for (j = 0; j < jj; j++) mat[i][j] = y[k++];
        return err;
    }

    void atimes(VecDoub_I &x, VecDoub_O &r, const Int itrnsp) {
        // 稀疏矩阵及其转置的乘法运算。
        // 本例程体现了方程 (3.8.4)、(3.8.5) 和 (3.8.6)。
        Int i, j, k, n = r.size(), jjt, it;
        Doub del;
        for (k = 0; k < n; k++) r[k] = 0.;
        for (k = 0; k < n; k++) {
            i = k / jj;
            j = k - i * jj;
            if (mask[k]) {
                r[k] += x[k];
            } else if (i > 0 && i < ii - 1 && j > 0 && j < jj - 1) {
                if (itrnsp) {
                    r[k] += x[k];
                    del = -0.25 * x[k];
                    r[k - 1] += del;
                    r[k + 1] += del;
                    r[k - jj] += del;
                    r[k + jj] += del;
                } else {
                    r[k] = x[k] - 0.25 * (x[k - 1] + x[k + 1] + x[k - jj] + x[k + jj]);
                }
            } else if (i > 0 && i < ii - 1) {
                if (itrnsp) {
                    r[k] += x[k];
                    del = -0.5 * x[k];
                    r[k - jj] += del;
                    r[k + jj] += del;
                } else {
                    r[k] = x[k] - 0.5 * (x[k - jj] + x[k + jj]);
                }
            } else if (j > 0 && j < jj - 1) {
                if (itrnsp) {
                    r[k] += x[k];
                    del = -0.5 * x[k];
                    r[k - 1] += del;
                    r[k + 1] += del;
                } else {
                    r[k] = x[k] - 0.5 * (x[k - 1] + x[k + 1]);
                }
            } else {
                jjt = (i == 0) ? jj : -jj;
                it = (j == 0) ? 1 : -1;
                if (itrnsp) {
                    r[k] += x[k];
                    del = -0.5 * x[k];
                    r[k + jjt] += del;
                    r[k + it] += del;
                } else {
                    r[k] = x[k] - 0.5 * (x[k + jjt] + x[k + it]);
                }
            }
        }
    }
};

使用非常简单：只需在已知函数值的位置填入数值，在未知位置填入 1.e99；将矩阵传给构造函数；然后调用 solve 例程即可。缺失值将被插值填充。在大多数情况下，默认参数就足够了。

Int m = ..., n = ...; MatDoub mat(m, n); ...
Laplaceinterp mylaplace(mat);
mylaplace.solve();

对于 $300\times 300$ 的矩阵，若其中随机 10% 的网格点具有已知函数值，其余 90% 通过插值得到，则可获得相当不错的结果。然而，由于计算时间随 $MN\max (M,N)$（即立方级）增长，除非将大矩阵分割成重叠的小块，否则该方法不适用于更大的矩阵。如果遇到收敛困难，应多次连续调用 solve（使用适当的非默认参数），并在每次调用后检查返回的误差估计。

3.8.1 最小曲率方法

拉普拉斯插值倾向于在被大量未知点包围的小块已知数据点周围产生锥形尖峰。其原因是，在二维情况下，拉普拉斯方程在点源附近的解具有对数奇异性。当已知数据在网格上分布相对均匀（即使随机）时，这通常不是问题。最小曲率方法则通过采用双调和方程

$${\nabla }^{4}v=0$$

而非拉普拉斯方程，从更根本的层面处理该问题。双调和方程的解使曲率平方的积分

$${\int }_{\Omega }|{\nabla }^{2}y{|}^{2}d\Omega$$

达到最小。最小曲率方法在地球科学领域被广泛使用 [3,4]。

参考文献中还给出了多种可用于缺失数据插值和网格化的其他方法。

参考文献

Noma, A.A. and Misulia, M.G. 1959, "Programming Topographic Maps for Automatic Terrain Model Construction," Surveying and Mapping, vol. 19, pp. 355-366.[1]

Crain, I.K. 1970, "Computer Interpolation and Contouring of Two-dimensional Data: a Review," Geoexploration, vol. 8, pp. 71-86.[2]

Burrough, P.A. 1998, Principles of Geographical Information Systems, 2nd ed. (Oxford, UK: Clarendon Press)

Watson, D.F. 1982, Contouring: A Guide to the Analysis and Display of Spatial Data (Oxford, UK: Pergamon).

Briggs, I.C. 1974, "Machine Contouring Using Minimum Curvature," Geophysics, vol. 39, pp. 39-48.[3]

Smith, W.H.F. and Wessel, P. 1990, "Gridding With Continuous Curvature Splines in Tension," Geophysics, vol. 55, pp. 293-305.[4]

本章解析PDF