4.0 引言
数值积分(也称为求积)的历史可追溯至微积分的发明甚至更早。由于初等函数的积分通常无法解析求解,而导数却可以,这一事实使得数值积分领域在18世纪和19世纪整个时期内显得格外引人注目,并使其地位高于数值分析中那些枯燥的算术运算。
随着自动计算的出现,求积变成了众多数值任务中普通的一项,甚至不再特别有趣。即便是最原始的自动计算方式——使用台式计算器和满屋子的“计算员”(在1950年代之前,“computer”指的是人而非机器)——也使得数值求解微分方程这一更为丰富的领域变得切实可行。求积只不过是其中最简单的特例:计算积分
等价于求解微分方程
在边界条件
下,得到 的值。
本书第17章讨论微分方程的数值积分。在该章中,我们着重强调了“变步长”或“自适应”步长选择的概念。因此,我们在此不再展开相关内容。如果你打算积分的函数在一个或多个尖峰处高度集中,或者其形状无法用单一的长度尺度来描述,那么你很可能应该将问题转化为(4.0.2)–(4.0.3)的形式,并使用第17章中的方法。(但请先阅读§4.7。)
本章中的求积方法,或多或少都基于一个显而易见的策略:在积分区间内选取一系列横坐标点,对被积函数在这些点上的值进行累加。目标是以尽可能少的函数求值次数,获得尽可能精确的积分结果。正如插值(第3章)的情形一样,你可以自由选择不同阶数的方法;高阶方法有时(但并非总是)能带来更高的精度。§4.3中讨论的龙贝格积分(Romberg integration)是一种通用形式体系,能够综合利用多种不同阶数的积分方法,我们强烈推荐使用。
除了本章及第17章的方法外,还有其他获取积分的方法。其中一类重要的方法基于函数逼近。我们在§5.9中明确讨论了利用切比雪夫逼近(Clenshaw-Curtis求积)对函数进行积分。虽然此处未明确讨论,但你应该能够利用§3.3中样条函数(spline)程序的输出结果,自行推导出三次样条求积的方法。(提示:对公式3.3.3关于 进行解析积分。参见[1]。)
某些与傅里叶变换相关的积分可以利用快速傅里叶变换(FFT)算法进行计算,这在§13.9中有讨论。另一个相关的问题是计算具有长振荡尾部的积分,这在§5.3末尾有所讨论。
多维积分则是另一个完全不同的、更为复杂的问题。本章的§4.8对此进行了初步讨论;而蒙特卡洛积分这一重要技术则在第7章中介绍。
参考文献
Carnahan, B., Luther, H.A., and Wilkes, J.O. 1969, Applied Numerical Methods (New York: Wiley), Chapter 2.
Isaacson, E., and Keller, H.B. 1966, Analysis of Numerical Methods; reprinted 1994 (New York: Dover), Chapter 7.
Acton, F.S. 1970, Numerical Methods That Work; 1990, corrected edition (Washington, DC: Mathematical Association of America), Chapter 4.
Stoer, J., and Bulirsch, R. 2002, Introduction to Numerical Analysis, 3rd ed. (New York: Springer), Chapter 3.
Ralston, A., and Rabinowitz, P. 1978, A First Course in Numerical Analysis, 2nd ed.; reprinted 2001 (New York: Dover), Chapter 4.
Dahlquist, G., and Bjorck, A. 1974, Numerical Methods (Englewood Cliffs, NJ: Prentice-Hall); reprinted 2003 (New York: Dover), §7.4.
Kahaner, D., Moler, C., and Nash, S. 1989, Numerical Methods and Software (Englewood Cliffs, NJ: Prentice-Hall), Chapter 5.
Forsythe, G.E., Malcolm, M.A., and Moler, C.B. 1977, Computer Methods for Mathematical Computations (Englewood Cliffs, NJ: Prentice-Hall), §5.2, p. 89.[1]
Davis, P., and Rabinowitz, P. 1984, Methods of Numerical Integration, 2nd ed. (Orlando, FL: Academic Press).
4.1 等距横坐标的经典公式
一本关于数值分析的书,若没有辛普森先生和他的“法则”,那将是不可想象的。对于在等距节点上已知函数值的情形,经典的积分公式具有一种独特的优雅,并且充满了历史韵味。通过这些公式,现代数值分析工作者得以与几个世纪以来的前辈们——甚至可追溯至牛顿时代或更早——进行精神上的交流。可惜时代在变;除了其中两个最简单的公式(“扩展梯形法则”,公式4.1.11,以及“扩展中点法则”,公式4.1.19;见§4.2)之外,这些经典公式几乎已完全失去实用价值。它们如今只是博物馆中的展品,但却是美丽的展品;我们现在就进入这座博物馆。(如果你对“观光”不感兴趣,可以直接跳到§4.2。)
一些记号说明:我们有一组横坐标点,记为 , , , , ,它们之间的间距为常数 ,
函数 在这些点 上的值已知,
我们希望在下限 和上限 之间对函数 进行积分,其中 和 各自等于某个 。若积分公式使用了端点处的函数值 或 ,则称为闭型公式。有时,我们希望积分的函数在一个或两个端点处难以计算(例如,函数在该处的计算形式为0/0的不定式,或者更糟的是存在可积的奇点)。此时,我们希望使用开型公式,即仅利用严格位于 和 之间的 来估计积分(见图4.1.1)。
经典公式的基石是在少量区间上积分函数的规则。随着区间数的增加,我们可以找到对更高次多项式精确成立的规则。(请注意,在实际应用中,更高阶数并不总意味着更高精度。)下面给出一系列这样的闭型公式。
4.1.1 闭型牛顿-科特斯公式
梯形法则:
此处的误差项 表示真实结果与估计值之间的差异为某个数值系数、 以及函数二阶导数在积分区间内某点处的值三者的乘积。该系数是已知的,可在本主题的所有标准参考文献中找到。然而,二阶导数应在哪一点取值却是未知的。如果我们知道这一点,就可以在那里计算函数值,从而得到更高阶的方法!由于已知量与未知量的乘积仍是未知的,我们将简化公式,仅写作 ,而不写出具体系数。
公式(4.1.3)是一个两点公式( 和 )。它对次数不超过1次的多项式(即 )是精确的。人们自然会预期存在一个三点公式,对次数不超过2次的多项式精确成立。这确实成立;而且,由于公式具有左右对称性,系数相互抵消,使得该三点公式实际上对次数不超过3次的多项式(即 )也是精确的。
辛普森法则:
这里 表示函数 在区间内某未知点处的四阶导数。还需注意,该公式用于计算长度为 的区间上的积分,因此系数之和为 2。
四点公式中没有幸运的抵消项,因此它对次数不超过 3 的多项式也是精确的。
辛普森 法则:
五点公式再次得益于某种抵消:
博德法则(Bode's rule):
该公式对次数不超过 5 的多项式是精确的。
至此,这些公式不再以著名人物命名,因此我们不再继续深入。更多序列中的公式可参见文献 [1]。
4.1.2 单区间外推公式
我们将暂时偏离历史惯例。许多教材在此处会给出一系列“开型牛顿-科特斯公式(Newton-Cotes Formulas of Open Type)”。例如:
注意,从 到 的积分仅使用了内点 进行估计。我们认为这类公式并不实用,原因有二:(i) 它们无法像闭型公式那样有效地拼接成“扩展”规则;(ii) 在其他所有可能的应用场景中,它们都被高斯积分公式(将在 §4.6 中介绍)所超越。
因此,我们不采用牛顿-科特斯开型公式,而是列出仅使用 处函数值 来估计单区间 上积分的公式。这些公式将成为后续“扩展开型公式”的有用构建模块。
或许有必要简要说明上述公式是如何推导的。虽然存在更优雅的方法,但最直接的方式是写出公式的基本形式,并将数值系数替换为未知数(例如 )。不失一般性,令 、,则 。依次将 (以及 )替换为函数 、、 和 。对每种情况计算积分,左边变为一个数值,右边则变为关于未知数 的线性方程。通过求解由此得到的四个方程,即可确定这些系数。
4.1.3 扩展公式(闭型)
若将公式 (4.1.3) 应用于区间 共 次,并将结果相加,即可得到从 到 的积分的“扩展”或“复合”公式。
扩展梯形法则:
此处我们将误差估计用区间长度 和点数 表示,而非用 表示。这样更清晰,因为通常 和 是固定的,人们更关心例如将步数加倍后误差会减少多少(在此情况下,误差减少为原来的四分之一)。在后续公式中,我们仅显示误差项随步数变化的阶数。
出于 §4.2 节才会阐明的原因,公式 (4.1.11) 实际上是本节最重要的公式;它是大多数实用数值积分方案的基础。
阶为 的扩展公式为:
(我们稍后将说明其来源。)
若将公式 (4.1.4) 应用于连续且不重叠的区间对,即可得到扩展辛普森法则:
注意,在内部求值点上,系数以 、 交替出现。许多人认为这种交替波动蕴含了关于其函数积分的深刻信息,而这些信息是肉眼无法察觉的。实际上,这种交替只是使用基本单元 (4.1.4) 所导致的人为现象。另一种与辛普森法则具有相同阶数的扩展公式是:
该公式通过在连续的四点组上拟合三次多项式构造而成;具体细节我们推迟到 §19.3 节讨论,那里在求解积分方程时使用了类似技术。不过,我们可以说明公式 (4.1.12) 的来源:它是辛普森扩展法则与其自身的一个修改版本的平均,其中首尾两步使用梯形法则 (4.1.3)。梯形法则比辛普森法则低两阶;然而,由于它仅使用两次而非 次,其对积分的贡献随 的额外幂次衰减。这使得最终公式的精度比辛普森法则低一阶。
4.1.4 扩展公式(开型与半开型)
我们可以通过将闭型公式 (4.1.11)–(4.1.14)(用于第二步及后续步骤)与第一步的外推开型公式 (4.1.7)–(4.1.10) 相加,来构造开型和半开型扩展公式。如前所述,使用比(重复的)内部步骤低一阶的端点步骤是自洽的。由此得到的两端均为开区间的公式如下。
公式 (4.1.7) 与 (4.1.11) 给出
式 (4.1.8) 和 (4.1.12) 给出
式 (4.1.9) 和 (4.1.13) 给出
内部点的系数在 和 之间交替。如果我们希望避免这种交替,可以将式 (4.1.9) 和 (4.1.14) 结合,得到
顺便提一下另一种扩展的开型公式,适用于积分限位于表格横坐标中点之间的情形。该公式称为扩展中点法则,其精度阶数与 (4.1.15) 相同:
对于这种情况也存在更高阶的公式,但我们不再给出。
半开型公式就是将式 (4.1.11)–(4.1.14) 分别与式 (4.1.15)–(4.1.18) 显然地组合而成。在积分区间的闭端,使用前一组公式的权重;在开端,使用后一组公式的权重。
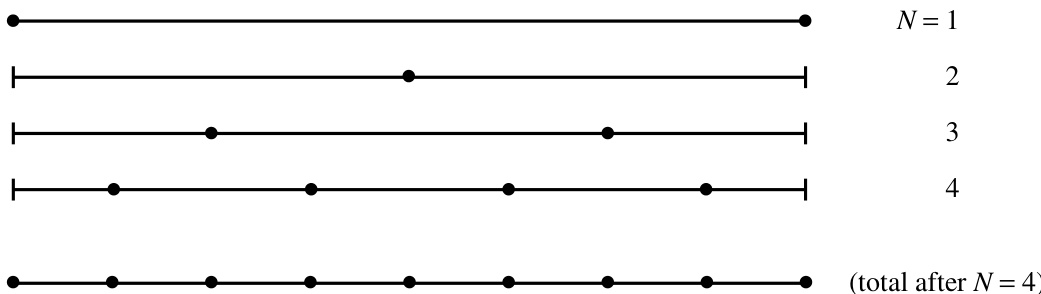
图 4.2.1. 对例程 Trapzd 的连续调用会保留之前调用的信息,并仅在细化网格所必需的新点上计算被积函数。最底行显示了第四次调用后所有函数求值的总和。例程 qsimp 通过对中间结果加权,将梯形法则转换为辛普森法则,而几乎不增加额外开销。
例如,下面这个公式的误差项以 的速率减小,其右端为闭型、左端为开型:
参考文献
Abramowitz, M., and Stegun, I.A. 1964, Handbook of Mathematical Functions (Washington: National Bureau of Standards); 1968 年重印 (New York: Dover); 在线版见 http://www.nr.com/aands, §25.4.[1]
Isaacson, E., and Keller, H.B. 1966, Analysis of Numerical Methods; 1994 年重印 (New York: Dover), §7.1.
4.2 基本算法
我们的起点是式 (4.1.11),即扩展梯形法则。梯形法则有两个特性,使其成为多种算法的起点。一个特性相当明显,而另一个则较为“深刻”。
明显的特性是:对于在固定区间 上积分的固定函数 ,在扩展梯形法则中将区间数加倍时,不会丢失之前计算的成果。梯形法则最粗糙的实现是取函数在端点 和 处的平均值。第一次细化是在该平均值基础上加上函数在中点处的值。第二次细化是加上函数在 1/4 和 3/4 点处的值,依此类推(见图 4.2.1)。
正如我们将看到的,许多基本数值积分算法都涉及逐级细化。将这一特性封装在一个 Quadrature 结构中是很方便的:
struct Quadrature {
// 基本数值积分算法的抽象基类。
Int n; // 当前细化级别。
virtual Doub next() = 0;
// 返回第 n 级细化时的积分值。
// 函数 next() 必须在派生类中定义。
};
然后,Trapzd 结构由此派生如下:
template<class T>
struct Trapzd : Quadrature {
// 实现扩展梯形法则的例程。
Doub a, b, s;
T &func;
Trapzd(T &funcc, const Doub aa, const Doub bb) :
func(funcc), a(aa), b(bb) { n = 0; }
// 构造函数接收待积分的函数或函子 func,以及积分限 a 和 b。
Doub next() {
// 返回扩展梯形法则的第 n 级细化结果。
// 第一次调用 (n=1) 时,返回积分 \int_a^b f(x)dx 的最粗糙估计。
// 后续调用设 n=2,3,...,通过增加 2^{n-2} 个新的内点来提高精度。
Doub x, tnm, sum, del;
Int it, j;
n++;
if (n == 1) {
return (s = 0.5 * (b - a) * (func(a) + func(b)));
} else {
for (it = 1, j = 1; j < n - 1; j++) it <<= 1;
tnm = it;
del = (b - a) / tnm;
x = a + 0.5 * del;
for (sum = 0.0, j = 0; j < it; j++, x += del) sum += func(x);
s = 0.5 * (s + (b - a) * sum / tnm);
return s;
}
}
};
注意,Trapzd 是对整个结构体进行模板化,而不仅仅包含一个模板函数。这是因为该结构体需要将传入的函数或函子作为成员变量保留下来。
Trapzd 结构是一个多用途的工具,有多种使用方式。最简单(也最粗糙)的方式是当你预先知道(我们难以想象如何知道!)所需步数时,直接用扩展梯形法则进行积分。如果你想要 个点,可以通过以下代码片段实现:
Ftor func;
Trapzd<Ftor> s(func, a, b);
for (j = 1; j <= M + 1; j++) val = s.next();
// 此处的函子 func 不带参数。
结果以 val 返回。这里 Ftor 是包含待积函数的函子。
当然,更好的方法是不断细化梯形法则,直到达到指定的精度。为此编写的函数如下:
template<class T>
Doub qtrap(T &func, const Doub a, const Doub b, const Doub eps = 1.0e-10) {
// 返回函数或函子 func 从 a 到 b 的积分。
// 常量 EPS 可设为期望的相对精度,JMAX 设定最大允许步数为 2^{JMAX-1}。
// 积分通过梯形法则完成。
const Int JMAX = 20;
Doub s, olds = 0.0;
Trapzd<T> t(func, a, b);
for (Int j = 0; j < JMAX; j++) {
s = t.next();
if (j > 5)
if (abs(s - olds) < eps * abs(olds) ||
(s == 0.0 && olds == 0.0)) return s;
olds = s;
}
throw("Too many steps in routine qtrap");
}
可选参数 eps 设置期望的相对精度。尽管 qtrap 看似简单,但对于不太光滑的函数,它实际上是一种相当稳健的积分方法。更复杂的方法通常意味着更高阶的算法,但其效率优势仅在被积函数足够光滑时才能体现。例如,当被积函数是基于测量数据点线性插值得到的变量的函数时,qtrap 是首选方法。但要注意不要将 eps 设得过于严格:如果 qtrap 为达到所需精度而进行过多步迭代,累积的舍入误差可能开始增大,导致例程无法收敛。在双精度下,若收敛速度适中, 甚至更小的精度通常没有问题,否则则不然。(当然,极少有实际问题真正需要如此高的精度。)
现在我们讨论扩展梯形法则(式 (4.1.11))的“深刻”事实:该近似的误差从 项开始,而当用 的幂次表示时,误差实际上完全是偶次幂项。这可直接由欧拉-麦克劳林求和公式得出:
其中 是伯努利数,由生成函数定义:
前几个偶数项的值如下(奇数项除 外均为零):
公式 (4.2.1) 并非一个收敛展开式,而只是一个渐近展开式,其截断误差在任意截断点处的绝对值总是小于被忽略的第一项绝对值的两倍。之所以不收敛,是因为伯努利数增长得非常快,例如:
关键点在于,(4.2.1) 的误差级数中仅包含 的偶次幂。这一性质通常并不适用于 §4.1 中的高阶求积公式。例如,公式 (4.1.12) 的误差级数以 开始,但随后包含所有更高次幂:、 等。
假设我们用 步计算 (4.1.11),得到结果 ,再用 步计算,得到结果 。(这可通过连续两次调用 Trapzd 实现。)第二次计算的主导误差项将是第一次误差项大小的 。因此,组合
将消除主导阶的误差项。而根据 (4.2.1),不存在 阶的误差项,剩余误差为 阶,与辛普森法则相同。事实上,不难看出 (4.2.4) 正是辛普森法则 (4.1.13),其系数交替为 、 等。这是计算该法则的优选方法,我们可以将其编写为与上述 qtrap 完全类似的例程:
template<class T>
Doub qsimp(T &func, const Doub a, const Doub b, const Doub eps=1.0e-10) {
// 返回函数或函数对象 func 在 a 到 b 区间上的积分。
// 常量 EPS 可设为期望的相对精度,JMAX 设为最大允许步数(步数为 2^(JMAX-1))。
// 积分采用辛普森法则。
const Int JMAX=20;
Doub s, st, ost=0.0, os=0.0;
Trapzd<T> t(func,a,b);
for (Int j=0;j<JMAX;j++) {
st=t.next();
s=(4.0*st-ost)/3.0;
if (j > 5)
if (abs(s-os) < eps*abs(os) ||
(s == 0.0 && os == 0.0)) return s;
os=s;
ost=st;
}
throw("Too many steps in routine qsimp");
}
当被积函数具有有限的四阶导数(即三阶导数连续)时,例程 qsimp 通常比 qtrap 更高效(即需要更少的函数求值)。qsimp 与其必需的辅助例程 Trapzd 的组合非常适合轻量级任务。
参考文献
Stoer, J., and Bulirsch, R. 2002, Introduction to Numerical Analysis, 3rd ed. (New York: Springer), §3.1.
Dahlquist, G., and Bjorck, A. 1974, Numerical Methods (Englewood Cliffs, NJ: Prentice-Hall); reprinted 2003 (New York: Dover), §7.4.1 – §7.4.2.
Forsythe, G.E., Malcolm, M.A., and Moler, C.B. 1977, Computer Methods for Mathematical Computations (Englewood Cliffs, NJ: Prentice-Hall), §5.3.
4.3 龙贝格积分
我们可以将龙贝格方法视为上一节中 qsimp 例程向高于辛普森法则阶数的积分方案的自然推广。其基本思想是利用扩展梯形法则(由 trapzd 实现)连续 次细化的结果,消除误差级数中直至(但不包括) 的所有项。qsimp 对应 的情形。这是“理查森延迟极限法”(Richardson's deferred approach to the limit)这一普遍思想的一个实例:对参数 的不同取值执行某种数值算法,然后将结果外推至连续极限 。
公式 (4.2.4) 通过减去主导误差项,是多项式外推的一个特例。在更一般的龙贝格情形中,我们可以使用 Neville 算法(见 §3.2)将连续细化结果外推至步长为零的情形。事实上,Neville 算法可以非常简洁地编码到龙贝格积分例程中。然而,为了程序清晰起见,似乎通过调用 §3.2 中给出的 Polyinterp::rawinterp 函数进行外推更为合适。
template <class T>
Doub qromb(T &func, Doub a, Doub b, const Doub eps=1.0e-10) {
// 返回函数或函数对象 func 在 a 到 b 区间上的积分。
// 积分采用龙贝格方法,阶数为 2K;例如 K=2 对应辛普森法则。
const Int JMAX=20, JMAXP=JMAX+1, K=5;
// EPS 为期望的相对精度,由外推误差估计确定;
// JMAX 限制总步数;K 为外推所用点数。
VecDoub s(JMAX), h(JMAXP);
Polyinterp point(h,s,K);
h[0]=1.0;
Trapzd<T> t(func,a,b);
for (Int j=1;j<=JMAX;j++) {
s[j-1]=t.next();
if (j >= K) {
Doub ss=point.rawinterp(j-K,0.0);
if (abs(point.dy) <= eps*abs(ss)) return ss;
}
h[j]=0.25*h[j-1];
// 这是关键一步:因子为 0.25,尽管步长仅减半。
// 这使得外推成为 $h^2$ 的多项式(如公式 (4.2.1) 所允许),而不仅是 $h$ 的多项式。
}
throw("Too many steps in routine qromb");
}
对于足够光滑(例如解析)的被积函数,在不含奇点的区间上积分,且端点也非奇异的情形下,例程 qromb 非常强大。在此类情况下,qromb 所需的函数求值次数远少于 §4.2 中的任一例程。例如,积分
在上述参数设置下,仅需 6 次 trapzd 调用(第二次外推时)即可收敛,而 qsimp 需要 11 次调用(被积函数求值次数为其 32 倍),qtrap 则需 19 次调用(被积函数求值次数为其 8192 倍)。
参考文献
Stoer, J., and Bulirsch, R. 2002, Introduction to Numerical Analysis, 3rd ed. (New York: Springer), §3.4 – §3.5.
Dahlquist, G., and Bjorck, A. 1974, Numerical Methods (Englewood Cliffs, NJ: Prentice-Hall); reprinted 2003 (New York: Dover), §7.4.1 – §7.4.2.
Ralston, A., and Rabinowitz, P. 1978, A First Course in Numerical Analysis, 2nd ed.; reprinted 2001 (New York: Dover), §4.10–2.
4.4 反常积分
就本文目的而言,若积分存在以下任一问题,则称为“反常”:
- 被积函数在有限上下限处趋于有限极限值,但在其中一个端点处无法直接求值(例如 处的 )
- 上限为 ,或下限为
- 在任一端点处存在可积奇点(例如 处的 )
- 在上下限之间的已知位置存在可积奇点
- 在上下限之间的未知位置存在可积奇点
若积分发散(例如 ),或在极限意义下不存在(例如 ),我们不称其为反常积分,而称其为不可能积分。无论采用多么巧妙的算法,都无法对一个不适定问题给出有意义的答案。
本节将推广前两节的技术,以处理上述列表中的前四个问题。关于含可积奇点的求积法的更深入讨论见第 19 章,尤其是 §19.3。第五个问题(奇点位置未知)只能通过变步长微分方程积分例程(见第 17 章)或自适应求积例程(如 §4.7)处理。
我们需要一个类似于扩展梯形法则(公式 4.1.11)的基础例程,但要求是 §4.1 意义上的开式公式,即不要求在端点处计算被积函数。公式 (4.1.19)(扩展中点法则)是最佳选择。原因在于,(4.1.19) 与 (4.1.11) 一样,具有“深层”性质:其误差级数完全由 的偶次幂组成。事实上,存在一个不太为人所知的公式,称为第二欧拉-麦克劳林求和公式:
该公式可通过将 (4.2.1) 以步长 写出,再以步长 写出,然后用后者的两倍减去前者而导出。
在扩展中点法则中,无法通过将步数加倍而同时保留先前的函数求值结果(不妨一试!)。但将步数增至三倍则可以做到。我们应选择三倍还是接受加倍带来的损失?平均而言,三倍步数会带来 倍的额外工作量,因为达到期望精度所需的“恰当”步数可能落在三倍步长所隐含的对数区间内的任意位置。对于加倍,该因子仅为 ,但因无法利用所有先前的求值结果而额外损失因子 2。由于 ,因此三倍步数更优。
以下是最终的结构,可直接与 Trapzd 进行比较。
template <class T>
struct Midpt : Quadrature {
// 实现扩展中点法则的例程。
Doub a, b, s;
T &funk;
Midpt(T &func, const Doub aa, const Doub bb) :
funk(func), a(aa), b(bb) { n = 0; }
// 构造函数接收 func(待在区间 [a, b] 上积分的函数或函数对象)以及积分限 a 和 b。
Doub next() {
// 返回扩展中点法则的第 i 次细化结果。
// 第一次调用(n=1)时,返回对 ∫ₐᵇ f(x)dx 的最粗略估计。
// 后续调用将 n 设为 2,3,...,并通过增加 (2/3)×3^{n−1} 个新的内点来提高精度。
Int it, j;
Doub x, tnm, sum, del, ddel;
n++;
if (n == 1) {
return (s = (b - a) * func(0.5 * (a + b)));
} else {
for (it = 1, j = 1; j < n - 1; j++) it *= 3;
tnm = it;
del = (b - a) / (3.0 * tnm);
ddel = del + del;
x = a + 0.5 * del;
sum = 0.0;
for (j = 0; j < it; j++) {
sum += func(x);
x += ddel;
sum += func(x);
x += del;
}
s = (s + (b - a) * sum / tnm) / 3.0;
return s;
}
}
virtual Doub func(const Doub x) { return funk(x); } // 恒等映射。
};
你可能已经注意到 Midpt 中似乎存在一层看似不必要的间接调用:它通过一个恒等函数 func 来调用用户提供的函数 funk。这样做的原因在于,我们将使用 funk 与 func 之间的非恒等映射,以解决前述的反常积分问题。新的积分方法只需从 Midpt 派生,并重写 func 即可。
结构 Midpt 可直接用于替代驱动例程(如 qtrap(§4.2))中的 Trapzd;只需将 Trapzd<T> t(func,a,b) 改为 Midpt<T> t(func,a,b),并可能减小参数 JMAX,因为
(步长三等分)远大于 (步长二等分)。
类似辛普森法则(§4.2 中的 qsimp)的开型公式实现也可用 Midpt 替代 Trapzd,同样减小 JMAX,但还需将外推步骤改为:
s = (9.0 * st - ost) / 8.0;
因为当步数变为三倍时,误差减小为原来的 1/9,而非步长加倍时的 1/4。
经上述修改后的 qtrap 或 qsimp 可解决本节开头列表中的第一个问题。更进一步、且能解决更多问题的方法是类似地推广龙贝格积分:
// romberg.h
template<class T>
Doub qromo(Midpt<T> &q, const Doub eps = 3.0e-9) {
// 开区间上的龙贝格积分。
// 使用任意指定的基本积分算法 q 和龙贝格方法返回函数的积分值。
// 通常 q 应为开型公式,不在端点处计算函数值。
// 假设 q 在每次调用时将步数增至三倍,且其误差级数仅包含步数的偶次幂。
// midpoint、midinf、midsql、midsqu、midexp 均可作为 q 的候选。
// 下方常量含义与 aromb 中相同。
const Int JMAX = 14, JMAXP = JMAX + 1, K = 5;
VecDoub h(JMAXP), s(JMAX);
Polyinterp point(h, s, K);
h[0] = 1.0;
for (Int j = 1; j <= JMAX; j++) {
s[j - 1] = q.next();
if (j >= K) {
Doub ss = point.rawinterp(j - K, 0.0);
if (abs(ss - s[j - 1]) <= eps * abs(ss)) return ss;
}
h[j] = h[j - 1] / 9.0; // 此处利用了步长三等分及误差级数为偶次幂的假设。
}
throw("Too many steps in routine qromo");
}
注意,我们现在传入的是一个 Midpt 对象,而非用户函数及积分限。这样做有充分的理由(如下所述)。但这意味着在调用 qromo 前需先将各部分绑定在一起,例如在区间 [a, b] 上积分时:
Midpt<Ftor> q(ftor, a, b);
Doub integral = qromo(q);
或对于普通函数:
Midpt<Doub(Doub)> q(fbare, a, b);
Doub integral = qromo(q);
宽松的 C++ 编译器允许你将其简化为:
Doub integral = qromo(Midpt<Ftor>(Ftor(), a, b));
或
Doub integral = qromo(Midpt<Doub(Doub)>(fbare, a, b));
但严格的编译器可能反对以引用方式传递临时对象,此时请使用上述两行形式。
正如我们将看到的,qromo 函数及其特殊接口,是解决我们首个列表中其他反常积分问题(除第五个棘手问题外)的优秀驱动例程。
处理反常积分的基本技巧是通过变量替换消除奇点,或将无穷积分区间映射为有限区间。例如,恒等式
可用于 且 ,或 且 的情形,适用于任何在无穷远处衰减快于 的函数。
你可以对 (4.4.2) 所示的变量替换进行解析处理,然后使用 qromo 和 Midpt 进行数值计算;也可以让数值算法自动完成变量替换。我们更倾向于后者,因其对用户更透明。为实现方程 (4.4.2),我们只需编写 Midpt 的修改版本 Midinf,允许 为无穷大(或更精确地说,为你机器上一个非常大的数,如 ),或 为负无穷大。由于 Midpt 中已具备所有机制,我们以派生类方式编写 Midinf,仅重写映射函数即可。
此例程是 midpnt 的完全替代品,即返回函数 func 在 [aa, bb] 上积分的第 n 次细化结果,但函数在 的等间距点上求值,而非在 上。这允许上限 bb 为计算机允许的最大正数,或下限 aa 为最大负数,但不能同时为无穷。aa 和 bb 必须同号。
Doub func(const Doub x) {
return Midpt<T>::funk(1.0 / x) / (x * x); // 实现变量替换
}
Midinf(T &funcc, const Doub aa, const Doub bb) :
Midpt<T>(funcc, aa, bb) {
Midpt<T>::a = 1.0 / bb;
Midpt<T>::b = 1.0 / aa;
}
例如,从 2 到 的积分可计算为:
Midinf<Ftor> q(ftor, 2.0, 1.0e99);
Doub integral = qromo(q);
若需从负下限积分到正无穷,可将积分在某个正值处分成两段,例如:
Midpt<Ftor> q1(ftor, -5.0, 2.0);
Midinf<Ftor> q2(ftor, 2.0, 1.0e99);
Doub integral = qromo(q1) + qromo(q2);
应如何选择分界点?应选一个足够大的正值,使得函数 funk 至少已开始趋近其在无穷远处的渐近衰减(趋于零)。对 qromo 的第二次调用中隐含的多项式外推处理的是关于 的多项式,而非关于 的多项式。
对于在积分下限处存在可积幂律奇点的积分,同样需进行变量替换。若被积函数在 附近发散为 (),则使用恒等式
若奇点在上限处,则使用恒等式
若两端点均有奇点,则如上例所示,在内部某点处分割积分。
在平方根倒数型奇点(实践中常见情形)下,方程 (4.4.3) 和 (4.4.4) 尤为简单:
适用于被积函数在 处有奇点的情形,以及
适用于被积函数在 处有奇点的情形。同样,我们可以通过为 Midpnt 定义替代例程来透明地实现这些变量替换,从而对用户自动完成变量变换:
template <class T>
struct Mysql : Midpnt<T> {
// 此例程是 midpnt 的完全替代品,不同之处在于它允许被积函数在下限 aa 处具有反平方根奇点。
Doub aorig;
Doub func(const Doub x) {
return 2.0 * x * Midpnt<T>::funk(aorig + x * x);
} // 执行变量替换。
Mysql(T &funcc, const Doub aa, const Doub bb) :
Midpnt<T>(funcc, aa, bb), aorig(aa) {
Midpnt<T>::a = 0;
Midpnt<T>::b = sqrt(bb - aa);
}
};
类似地,
template <class T>
struct Midsqu : Midpnt<T> {
// 此例程是 midpnt 的完全替代品,不同之处在于它允许被积函数在上限 bb 处具有反平方根奇点。
Doub borig;
Doub func(const Doub x) {
return 2.0 * x * Midpnt<T>::funk(borig - x * x);
} // 执行变量替换。
Midsqu(T &funcc, const Doub aa, const Doub bb) :
Midpnt<T>(funcc, aa, bb), borig(bb) {
Midpnt<T>::a = 0;
Midpnt<T>::b = sqrt(bb - aa);
}
};
最后一个例子足以说明这些公式通常是如何推导出来的。假设积分的上限为无穷大,且被积函数呈指数衰减。此时我们希望进行变量替换,将 映射为 (符号的选择应保证新变量的上限大于下限)。通过直接积分可得:
因此,
对用户透明的实现如下:
template <class T>
struct Midexp : Midpnt<T> {
// 此例程是 midpnt 的完全替代品,不同之处在于 bb 被假定为无穷大(传入的值实际上未被使用)。
// 假定函数 funk 在无穷远处呈指数快速衰减。
Doub func(const Doub x) {
return Midpnt<T>::funk(-log(x)) / x;
} // 执行变量替换。
Midexp(T &funcc, const Doub aa, const Doub bb) :
Midpnt<T>(funcc, aa, bb) {
Midpnt<T>::a = 0.0;
Midpnt<T>::b = exp(-aa);
}
};
参考文献
4.5 通过变量变换实现数值积分
设想一种简单的通用数值积分算法,它收敛速度极快,并且能完全忽略端点处的奇异性。听起来是不是太美好而难以置信?在本节中,我们将介绍一种实际上能以这种方式处理大量积分问题的算法。
考虑计算积分
正如我们在构造公式 (4.1.11)–(4.1.20) 时所见,通过调整端点附近的权重,可以构造出任意高阶的求积公式,其内部权重均为 1。但如果函数在端点附近衰减得足够快,那么这些权重就完全无关紧要了。在这种情况下,采用均匀权重的 点求积公式会以指数速度随 收敛。(关于这一思想更严格的理论依据,参见 §4.5.1;关于其与高斯求积的联系,参见 §20.7.4 末尾的讨论。)
如果函数在端点处不为零怎么办?考虑变量替换 ,使得 :
选择变换使得因子 在区间端点处迅速趋于零。那么对 (4.5.2) 式应用简单的梯形法则即可得到极其精确的结果。(在本节中,我们将均匀权重的求积称为梯形求积,至于端点权重取 1/2 还是 1,则取决于个人偏好,因为它们实际上并不重要。)
即使 在区间端点处存在可积奇点,也可以通过合适的变换 使其影响被完全压制。我们无需针对奇点的具体性质定制变换:我们将讨论几种能有效消除几乎所有类型端点奇点的变换。
这类变换最早由 Schwartz [1] 提出,现被称为 TANH 规则:
当 时, 的急剧衰减解释了该算法的高效性及其处理奇点的能力。另一种类似的算法是 IMT 规则 [2]。然而,IMT 规则的 没有简单的解析表达式,且其性能与 TANH 规则相差不大。
使用 TANH 规则时需考虑两类误差。离散化误差即截断误差,源于使用梯形法则近似 。截断误差则是由于在有限的 处截断梯形法则中的无穷级数所致。(注意,现在的积分限已是 。)你可能会认为, 在 时衰减得越剧烈,算法效率就越高。但如果衰减过于剧烈,则原始区间 中心附近的求积点密度会很低,导致离散化误差很大。最优策略是使离散化误差与截断误差大致相等。
对于 TANH 规则,Schwartz [1] 证明离散化误差的阶为
其中 是被积函数最近的奇点到实轴的距离。当 时会出现极点,即 。如果 在更靠近实轴的位置没有极点,则 。另一方面,截断误差为
令 ,可得最优步长 及对应误差为
注意, 随 的衰减速度比任何 的幂次都快。如果 在端点处有奇点,这可能会修改 的表达式 (4.5.5)。通常会导致 (4.5.6) 式中的常数 减小。与其开发一种对每个被积函数都预先估计最优 的算法,我们更推荐采用简单的步长加倍法并检验收敛性。我们预期当 接近 (4.5.6) 式给出的值时,收敛性就会显现。
TANH 规则本质上使用指数映射来实现在无穷远处所需的快速衰减。基于“越多越好”的理念,可以尝试重复该过程,从而得到 DE(双指数)规则:
此处常数 通常取 1 或 。(当 时并无益处,因为在 时 ,但更大的 会使 迅速减小。)通过类似于 (4.5.4)–(4.5.6) 式的分析,可以证明 DE 规则的最优 及对应误差的阶为
其中 为常数。通过比较公式 (4.5.6) 与 (4.5.8) 所示,DE 规则相较于 TANH 规则具有更优的性能,这一结论在实践中得到了验证。
4.5.1 梯形法则的指数收敛性
使用梯形法则计算积分 (4.5.1) 时的误差由欧拉-麦克劳林求和公式给出:
注意,这通常是一个渐近展开式,而非收敛级数。若函数 的所有导数在端点处均为零,则公式 (4.5.9) 中的所有“修正项”均为零。此时误差极小——其随 趋于零的速度快于 的任意次幂。我们称该方法具有指数收敛性。因此,对于像 这类在 上所有导数在端点处均趋于零的函数,标准梯形法则是极佳的积分方法。
对于导数在端点处不全为零的函数,若变换满足 及其所有导数在区间端点处趋于零,则仍可实现指数收敛。若函数在端点处存在奇异性,则要求 及其所有导数在端点处为零。这是对前文所述“ 快速趋于零”的更精确表述。
4.5.2 实现
实现 DE 规则稍显棘手。直接对函数 使用 Trapzd 并非良策。首先,公式 (4.5.7) 中的因子 在通过 计算 时可能发生溢出。我们遵循文献 [3],引入变量 定义为
(为简化起见取 ),从而有
当 为较大的正值时, 会无害地下溢至零。对于负的 ,则利用梯形法则关于区间中点的对称性进行处理。我们写作
其中
第二个潜在问题是:在计算 或 时,舍入误差可能导致 在端点奇异性附近发散。为解决此问题,应将函数 编写为接受两个参数的函数 。此时可直接利用 计算奇异部分。例如,在 附近将函数 编码为 ,在 附近编码为 。(参见 §6.10 中另一个 的例子。)因此,下面的例程 Drule 要求函数 具有两个参数。若你的函数无奇异性,或奇异性“较弱”(例如不超过对数型),则在编写 时可忽略 ,直接按 编写即可。
例程 Drule 实现了公式 (4.5.12)。它包含一个参数 ,对应于变量 的上限。对 的首次近似由 (4.5.12) 右侧第一项给出,其中 。后续的改进则按常规方式将 逐次减半。在双精度计算中,通常取 ,对应 。这对对数型或更弱的奇异性通常已足够。若需对更强的奇异性获得高精度,则可能需要增大 。例如,对于 ,需取 才能达到完整的双精度精度。这对应于 ,正如预期。
构造函数。func 是提供被积函数的函数或函子,积分区间为输入的 aa 和 bb。func 中的函数运算符接受两个参数 和 ,如正文所述。在变换变量 下的积分区间为 (, )。对于对数型或更弱的奇异性, 的典型值为 3.7;对于平方根型奇异性,则为 4.3,如正文所述。
Doug next() i
首次调用函数 next(n=1)时,例程返回 的最粗略估计值。后续调用 next(n=2,3,...)将通过增加 个新的内点来提高精度。
Doub del,fact,q.sum,t,twoh;
Int it,j;
n++, if (n == 1) { fact=0.25; return s=hmax2.0(b-a)factfunc(0.5*(b+a),0.5*(b-a));
} else { for (it=1,j=1;j<n-1;j++) it << 1; twoh=hmax/it; // 待添加点的间距的两倍。 t=0.5twoh; for (sum=0.0,j=0;j<it;j++) { q=exp(-2.0sinh(t)); del=(b-a)q/(1.0+q); fact=q/SQR(1.0+q)cosh(t); sum += fact(func(a+del,del)+func(b-del,del)); t += twoh; } return s=0.5s+(b-a)twohsum; // 用改进后的值替换 s 并返回。 } }
若双指数规则(DE 规则)通常优于单指数规则(TANH 规则),为何不再进一步使用三重指数规则、四重指数规则……?如前所述,离散化误差主要由离实轴最近的极点决定。事实表明,超过双指数后,极点会越来越接近实轴,因此方法性能反而变差,而非更好。
若被积函数本身在靠近实轴处存在极点(比 DE 或 TANH 规则引入的 更近得多),则方法的收敛速度会减慢。在可解析处理的情形下,可通过向梯形法则添加一个“极点修正项”来恢复快速收敛 [4]。
4.5.3 无穷区间
若积分区间的一个或两个端点为无穷,可对 TANH 或 DE 规则稍作修改后使用:
| 区间 | TANH 规则 | DE 规则 | 混合规则 |
|---|---|---|---|
最后一列给出了适用于在无穷远处快速衰减(如 或 )的函数的混合规则。该规则在 处为 DE 规则,但在无穷远处仅为单指数规则。被积函数的指数衰减特性使其在无穷远处也表现出类似 DE 规则的行为。对于 的混合规则,可通过将区间拆分为 和 ,并在前一区间作代换 来构造。这样便得到两个定义在 上的积分。
在实现无穷区间的 DE 规则时,无需像有限区间 DE 规则那样采取特别预防措施。可直接将例程 Trapzd 作为 的函数使用,其调用的函数 func 返回 。因此,若 funk 是返回 的函数,则可按如下形式(以混合规则为例)定义函数 func:
x=exp(t-exp(-t)); dxdt=x*(1.0+exp(-t)); return funk(x)*dxdt;
并将 func 传递给 Trapzd。唯一需要注意的是积分区间的选取。应确保积分端点处对积分的贡献可忽略不计。例如,对于 ,区间 通常已足够。
4.5.4 示例
为展示这些方法的强大能力,考虑以下积分示例:
积分 (4.5.15) 可以很容易地用 DE 规则处理。该算法仅需约 30 次函数求值即可收敛到机器精度(),完全不受端点奇异性的影响。积分 (4.5.16) 是一个被积函数在原点处有奇异性、且在无穷远处衰减缓慢的例子。由于衰减缓慢,Midinf 例程表现极差。然而,通过变换 ,在对 在区间 上积分时,仅需约 30 次函数求值即可再次达到机器精度。相比之下,若采用变换 且 在区间 上积分,则需要约 500 次函数求值才能达到相同的精度。
积分 (4.5.17) 结合了原点处的奇异性与无穷远处的指数衰减特性。此时,“混合”变换 效果最佳,在 的区间 上积分仅需约 60 次函数求值。注意,此处指数衰减至关重要;对于像 这样缓慢衰减的振荡函数,这些变换会完全失效。幸运的是,§5.3 中介绍的级数加速算法在这种情况下效果很好。
最后一个积分 (4.5.18) 与 (4.5.17) 类似,使用相同的变换达到机器精度所需的函数求值次数也大致相同。由于被积函数衰减更快, 的积分区间可以更小,例如 。注意,对于所有这些积分,如果我们采用步长加倍法来判断积分是否收敛,则实际所需的函数求值次数是我们所引用数值的两倍,因为我们需要额外一组梯形法则的求值结果来确认收敛性。然而在许多情况下,你并不需要这额外的一组函数求值:一旦方法开始收敛,每次迭代的有效数字位数大约会翻倍。因此,你可以将收敛判据设为:当连续两次迭代结果在所需精度的平方根范围内一致时停止计算。这样最后一次迭代的结果就会具有大约所需的精度。即使不使用这一技巧,该方法对于处理各种困难积分仍表现出非凡的效率。
§6.10 中给出了一个使用 DE 规则处理有限和无限区间积分的扩展示例。在那里,我们提供了一个计算广义费米-狄拉克积分的例程:
另一个例子见 §4.6 中的 Stiel 例程。
4.5.5 与采样定理的关系
函数的 sinc 展开式为
其中 。该展开式对一类有限的解析函数是精确的。然而,它对其他函数也可能是一个很好的近似,采样定理刻画了这类函数,将在 §13.11 中讨论。在那里,我们将利用 的 sinc 展开来近似复误差函数。能被 sinc 展开良好近似的函数通常在 时迅速衰减,因此即使将展开式截断到 ,仍能对 给出良好近似。
若对等式 (4.5.20) 两边积分,可得
这正是梯形公式!因此,梯形公式对 的积分快速收敛,等价于 能被其 sinc 展开良好近似。前面描述的各种变换可用于映射 ,从而在 上均匀采样得到良好的 sinc 近似。这些近似不仅可用于 的梯形求积,还可用于导数、积分变换、柯西主值积分以及微分和积分方程的求解 [5]。
参考文献
Schwartz, C. 1969, "Numerical Integration of Analytic Functions," Journal of Computational Physics, vol. 4, pp. 19–29.[1]
Iri, M., Moriguti, S., and Takasawa, Y. 1987, "On a Certain Quadrature Formula," Journal of Computational and Applied Mathematics, vol. 17, pp. 3–20. (English version of Japanese article originally published in 1970).[2]
Evans, G.A., Forbes, R.C., and Hyslop, J. 1984, "The Tanh Transformation for Singular Integrals," International Journal of Computer Mathematics, vol. 15, pp. 339–358.[3]
Bialecki, B. 1989, BIT, "A Modified Sinc Quadrature Rule for Functions with Poles near the Arc of Integration," vol. 29, pp. 464–476.[4]
Stenger, F. 1981, "Numerical Methods Based on Whittaker Cardinal or Sinc Functions," SIAM Review, vol. 23, pp. 165–224.[5]
Takahasi, H., and Mori, H. 1973, "Quadrature Formulas Obtained by Variable Transformation," Numerische Mathematik, vol. 21, pp. 206–219.
Mori, M. 1985, "Quadrature Formulas Obtained by Variable Transformation and DE Rule," Journal of Computational and Applied Mathematics, vol. 12&13, pp. 119–130.
Sikorski, K., and Stenger, F. 1984, "Optimal Quadratures in Spaces," ACM Transactions on Mathematical Software, vol. 10, pp. 140–151; op. cit., pp. 152–160.
4.6 高斯求积与正交多项式
在 §4.1 的公式中,函数的积分通过在一组等间距点上取函数值并乘以适当选择的权重系数之和来近似。我们发现,当允许更自由地选择这些系数时,可以得到更高阶的积分公式。高斯求积的思想是,不仅允许自由选择权重系数,还允许自由选择函数求值点(横坐标)的位置。这些点将不再是等间距的。因此,我们拥有的自由度数量将翻倍;结果表明,对于相同数量的函数求值,高斯求积公式的阶数基本上是牛顿-科特斯公式的两倍。
这听起来是不是太好了?从某种意义上说,确实如此。这里有一个熟悉的陷阱,再怎么强调也不为过:高阶并不等同于高精度。只有当被积函数非常光滑(即“能被多项式良好近似”)时,高阶才能转化为高精度。
然而,高斯求积公式还有一个额外特性,使其更加有用:我们可以选择权重和横坐标,使得积分对一类形如“多项式乘以某个已知函数 ”的被积函数精确成立,而不仅限于通常的“多项式”类被积函数。函数 可用于消除目标积分中的可积奇异性。换句话说,给定 和一个整数 ,我们可以找到一组权重 和横坐标 ,使得近似式
在 为多项式时精确成立。例如,对于积分
(必须承认,这不是一个很自然的积分),我们可能会对基于如下选择的高斯求积公式感兴趣:
在区间 上。(这种特定选择称为高斯-切比雪夫积分,原因很快就会明了。)
注意,积分公式 (4.6.1) 也可以写成权重函数 不显式出现的形式:定义 和 ,则 (4.6.1) 变为
函数 去哪儿了?它仍然隐含其中,随时准备对形如“多项式乘以 ”的被积函数提供高阶精度,同时也会拒绝为其他形式光滑且行为良好的被积函数提供高阶精度。当你查阅给定 的权重和横坐标表时,必须仔细确定它们是用于 (4.6.1) 形式的公式,还是用于 (4.6.4) 形式的公式。
到目前为止,我们对高斯求积的介绍相当标准。然而,该方法有一个方面并未得到应有的重视:对于光滑的被积函数(在提取适当的权重函数之后),随着 增加,高斯求积呈指数级快速收敛,因为该方法的阶数(而不仅仅是点的密度)随 增加而提高。这种行为应与基于牛顿-科特斯的方法的幂律行为(例如 或 )形成对比,后者即使点的密度增加,其阶数仍保持固定(例如 2 或 4)。更严格的讨论见 §20.7.4。
下面是一个求积例程的示例,其中包含了 且 时的横坐标和权重表。由于此时权重和横坐标关于积分区间中点对称,实际上每种仅有五个不同的值:
通过十点高斯-勒让德积分返回函数或函子 func 在 a 和 b 之间的积分值:函数在积分区间内部点上恰好求值十次。
以下是横坐标(abscissas)和权重(weights):
static const Doub x[] = {0.1488743389816312, 0.4333953941292472,
0.6794095682990244, 0.8650633666889845,
0.9739065285171717};
static const Doub w[] = {0.2955242247147529, 0.2692667193099963,
0.2190863625159821, 0.1494513491505806,
0.0666713443086881};
Doub xm = 0.5 * (b + a);
Doub xr = 0.5 * (b - a);
Doub s = 0;
for (Int j = 0; j < 5; j++) {
Doub dx = xr * x[j];
s += w[j] * (func(xm + dx) + func(xm - dx));
}
return s *= xr;
将结果缩放到积分区间。
上述例程说明,即使不完全理解高斯求积法背后的理论,也可以使用它:只需在书籍(例如 [1] 或 [2])中查找已制表的权重和横坐标即可。然而,该理论本身非常优美,当你需要为某个特殊的权函数 构造自己的权重和横坐标表时,这些理论知识将非常有用。因此,我们将不加证明地给出一些有用的结果,以帮助你完成这项工作。其中一些结果假设 在区间 内不变号,这在实际应用中通常是成立的。
高斯求积法的理论可追溯至 1814 年的高斯(Gauss),他利用连分式发展了这一主题。1826 年,雅可比(Jacobi)通过正交多项式重新推导了高斯的结果。而对任意权函数 使用正交多项式的系统性处理,主要归功于 1877 年的克里斯托费尔(Christoffel)。为了引入这些正交多项式,我们首先将感兴趣的区间固定为 。我们可以将“两个函数 和 在权函数 下的内积”定义为:
该内积是一个数值,而非 的函数。若两个函数的内积为零,则称它们正交。若一个函数与其自身的内积为 1,则称其已归一化。一组彼此相互正交且各自均已归一化的函数称为标准正交集(orthonormal set)。
我们可以找到一组多项式,满足:(i) 对每个 ,恰好包含一个 阶多项式 ;(ii) 所有多项式在给定的权函数 下相互正交。构造这样一组多项式的递推关系为:
其中
系数 是任意的;我们可以将其设为零。
由 (4.6.6) 定义的多项式是首一的(monic),即其最高次项 中的 的系数为 1。如果我们将每个 除以常数 ,就可以使这组多项式成为标准正交的。此外,也常遇到采用其他归一化方式的正交多项式。如果你知道 中 项的系数为 ,那么可以通过将每个 除以 得到首一多项式。注意,递推关系 (4.6.6) 中的系数依赖于所采用的归一化方式。
可以证明,多项式 在区间 内恰好有 个互异的根。此外,还可以证明 的根与 的 个根“交错”分布,即在后者的每两个相邻根之间,恰好有一个前者的根。这一性质在你需要寻找所有根时非常有用。你可以从 的唯一根开始,依次对更高阶的 进行根的定位,并在每一步通过牛顿法(Newton's rule)或其他求根方法(见第 9 章)更精确地确定这些根。
你为何需要寻找正交多项式 的所有根呢?因为对于区间 内权函数为 的 点高斯求积公式((4.6.1) 和 (4.6.4)),其横坐标恰好就是同一区间和权函数下正交多项式 的根。这是高斯求积法的基本定理,它使你能为任意具体情况找到横坐标。
一旦你知道了横坐标 ,就需要确定权重 ()。一种方法(并非最有效)是求解以下线性方程组:
方程 (4.6.8) 的目的就是求出那些权重,使得求积公式 (4.6.1) 对前 个正交多项式的积分给出正确结果。注意 (4.6.8) 右侧的零出现是因为 都与常数函数 正交。可以证明,采用这些权重时,接下来的 个多项式的积分也是精确的,因此该求积公式对所有次数不超过 的多项式都是精确的。另一种计算权重的方法(其证明超出了本书范围)由下式给出:
其中 是正交多项式在其零点 处的导数。
因此,高斯求积规则的计算包含两个不同的阶段:(i) 生成正交多项式 ,即计算 (4.6.6) 中的系数 、;(ii) 确定 的零点,并计算相应的权重。对于“经典”正交多项式的情形,系数 和 是显式已知的(见下文公式 4.6.10–4.6.14),因此可以省略阶段 (i)。然而,如果你面对的是一个“非经典”的权函数 ,且不知道系数 和 ,那么构造相应的正交多项式集就并非易事。我们将在本节末尾讨论这一问题。
4.6.1 横坐标与权重的计算
这一任务的难易程度取决于你对权函数及其相关多项式已有多少了解。对于经典且被深入研究过的正交多项式,几乎所有信息都是已知的,包括其零点的良好近似值。这些近似值可用作初始猜测,使牛顿法(将在 §9.4 中讨论)能够快速收敛。牛顿法需要导数 ,它可以通过 和 的标准关系式进行计算。权重则可方便地通过公式 (4.6.9) 计算。对于以下列出的几种情形,这种直接求根方法比其他任何方法快 3 到 5 倍。
以下是生成最常用正交多项式及其对应高斯求积公式的权函数、区间和递推关系。
高斯-勒让德(Gauss-Legendre):
高斯-切比雪夫(Gauss-Chebyshev):
高斯-拉盖尔(Gauss-Laguerre):
高斯-埃尔米特(Gauss-Hermite):
高斯-雅可比:
其中系数 、、 和 由下式给出:
我们现在给出针对这些情形分别计算横坐标(abscissas)和权重(weights)的子程序。首先是使用最广泛的横坐标和权重,即高斯-勒让德(Gauss-Legendre)情形。该子程序由 G.B. Rybicki 编写,使用了高斯-勒让德情形下公式 (4.6.9) 的特殊形式:
该子程序还将积分区间从 缩放至 ,并提供高斯求积公式所需的横坐标 和权重 :
void gauleg(const Doub x1, const Doub x2, VecDoub_0 &x, VecDoub_0 &w)
给定积分下限 和上限 ,该子程序返回长度为 的数组 和 ,其中包含 点高斯-勒让德求积公式的横坐标和权重。
const Doub EPS=1.0e-14;
Doub z1,z,xm,xl,pp,p3,p2,p1;
Int n=x.size();
Int m=(n+1)/2;
xm=0.5*(x2+x1);
xl=0.5*(x2-x1);
for (Int i=0;i<m;i++) {
z=cos(3.141592654*(i+0.75)/(n+0.5));
// 以该近似值作为第 i 个根的初始值,进入牛顿法主循环进行精化。
do {
p1=1.0;
p2=0.0;
for (Int j=0;j<n;j++) {
p3=p2;
p2=p1;
p1=((2.0*j+1.0)*z*p2-j*p3)/(j+1);
}
// p1 现在是所需的勒让德多项式。接下来利用涉及 p2(低一阶多项式)的标准关系计算其导数 pp。
pp=n*(z*p1-p2)/(z*z-1.0);
z1=z;
z=z1-p1/pp;
} while (abs(z-z1) > EPS);
x[i]=xm-xl*z;
x[n-1-i]=xm+xl*z;
w[i]=2.0*xl/((1.0-z*z)*pp*pp);
w[n-1-i]=w[i];
}
接下来给出三个使用 Stroud 和 Secrest [2] 提供的根初值近似的子程序。第一个用于高斯-拉盖尔(Gauss-Laguerre)横坐标和权重,适用于如下积分公式:
给定参数 (即拉盖尔多项式的参数 alf),该子程序返回数组 和 ,其中包含 点高斯-拉盖尔求积公式的横坐标和权重。最小的横坐标存于 ,最大的存于 。
const Int MAXIT=10;
const Doub EPS=1.0e-14;
Int i,its,j;
Doub ai,p1,p2,p3,pp,z,z1;
Int n=x.size();
for (i=0;i<n;i++) {
if (i == 0) {
z=(1.0+alf)*(3.0+0.92*alf)/(1.0+2.4*n+1.8*alf);
}
else if (i == 1) {
z += (15.0+6.25*alf)/(1.0+0.9*alf+2.5*n);
}
else {
ai=i-1;
// EPS 是相对精度。
// 对所需根进行循环。
// 最小根的初始猜测。
// 第二个根的初始猜测。
// 其他根的初始猜测。
z += ((1.0+2.55*ai)/(1.9*ai)+1.26*ai*alf/(1.0+3.5*ai))/(z-x[i-2])/(1.0+0.3*alf);
}
for (its=0;its<MAXIT;its++) {
p1=1.0;
p2=0.0;
for (j=0;j<n;j++) {
p3=p2;
p2=p1;
p1=((2.0+j+1.0+alf-z)*p2-(j+alf)*p3)/(j+1);
}
// p1 现在是所需的拉盖尔多项式。接下来利用涉及 p2(低一阶多项式)的标准关系计算其导数 pp。
pp=(n*p1-(n+alf)*p2)/z;
z1=z;
z=z1-p1/pp;
if (abs(z-z1) <= EPS) break;
}
if (its >= MAXIT) throw("too many iterations in gaulag");
x[i]=z;
// 存储根和权重。
w[i] = -exp(gammln(alf+n)-gammln(Doub(n)))/((pp*n+p2)*pp);
}
接下来是高斯-埃尔米特(Gauss-Hermite)横坐标和权重的子程序。如果我们使用公式 (4.6.13) 中给出的这些函数的“标准”归一化形式,会发现由于涉及各种阶乘,当 较大时计算会溢出。我们可以通过使用标准正交多项式 来避免这一问题。它们由如下递推关系生成:
此时权重公式变为:
而在此归一化下的导数公式为:
gauher 返回的横坐标和权重用于如下积分公式:
该子程序返回数组 和 ,其中包含 点高斯-埃尔米特求积公式的横坐标和权重。最大的横坐标存于 ,最小的(最负的)存于 。
const Doub EPS=1.0e-14,PIM4=0.7511255444649425;
// 相对精度和 $1/\pi^{1/4}$。
const Int MAXIT=10;
Int i,its,j,m; // 最大迭代次数。
Doub p1,p2,p3,pp,z,z1;
Int n=x.size();
m=(n+1)/2;
// 根关于原点对称,因此只需计算一半。
for (i=0;i<m;i++) {
if (i == 0) {
z=sqrt(Doub(2*n+1))-1.85575*pow(Doub(2*n+1),-0.16667);
} else if (i == 1) {
z -= 1.14*pow(Doub(n),0.426)/z;
} else if (i == 2) {
z=1.86*z-0.86*x[0];
} else if (i == 3) {
z=1.91*z-0.91*x[1];
} else {
z=2.0*z-x[i-2];
}
for (its=0;its<MAXIT;its++) {
p1=PIM4;
p2=0.0;
for (j=0;j<n;j++) {
p3=p2;
p2=p1;
p1=z*sqrt(2.0/(j+1))*p2-sqrt(Doub(j)/(j+1))*p3;
}
// p1 现在是所需的埃尔米特多项式。接下来利用关系式 (4.6.21) 和 p2(低一阶多项式)计算其导数 pp。
pp=sqrt(Doub(2*n))*p2;
z1=z;
z=z1-p1/pp;
if (abs(z-z1) <= EPS) break;
}
if (its >= MAXIT) throw("too many iterations in gauher");
x[i]=z;
x[n-1-i] = -z;
w[i]=2.0/(pp*pp);
w[n-1-i]=w[i];
}
最后,这里是高斯-雅可比(Gauss-Jacobi)横坐标和权重的子程序,用于实现如下积分公式:
void gaujac(VecDoub_0 &x, VecDoub_0 &w, const Doub alf, const Doub bet)
给定参数 (alf)和 (bet)(即雅可比多项式的参数),该子程序返回数组 和 ,其中包含 点高斯-雅可比求积公式的横坐标和权重。最大的横坐标存于 ,最小的存于 。
{
const Int MAXIT=10;
const Doub EPS=1.0e-14;
Int i,its,j;
Doub alfbet,an,bn,r1,r2,r3;
Doub a,b,c,p1,p2,p3,pp,temp,z,z1;
Int n=x.size();
for (i=0;i<n;i++) {
if (i == 0) {
// 最大根的初始猜测。
an=alf/n;
bn=bet/n;
r1=(1.0+alf)*(2.78/(4.0+n*n)+0.768*an/n);
r2=1.0+1.48*an+0.96*bn+0.452*an*an+0.83*an*bn;
z=1.0-r1/r2;
} else if (i == 1) {
// 第二大根的初始猜测。
r1=(4.1+alf)/((1.0+alf)*(1.0+0.156*alf));
r2=1.0+0.06*(n-8.0)*(1.0+0.12*alf)/n;
r3=1.0+0.012*bet*(1.0+0.25*abs(alf))/n;
z -= (1.0-z)*(r1*r2*r3);
} else if (i == 2) {
// 第三大根的初始猜测。
r1=(1.67+0.28*alf)/(1.0+0.37*alf);
r2=1.0+0.22*(n-8.0)/n;
r3=1.0+8.0*bet/((6.28+bet)*n*n);
z -= (x[0]-z)*r1*r2*r3;
} else if (i == n-2) {
// 第二小根的初始猜测。
r1=(1.0+0.235*bet)/(0.766+0.119*bet);
r2=1.0/(1.0+0.639*(n-4.0)/(1.0+0.71*(n-4.0)));
r3=1.0/(1.0+20.0*alf/((7.5+alf)*n*n));
z += (z-x[n-4])*r1*r2*r3;
} else if (i == n-1) {
// 最小根的初始猜测。
r1=(1.0+0.37*bet)/(1.67+0.28*bet);
r2=1.0/(1.0+0.22*(n-8.0)/n);
r3=1.0/(1.0+8.0*alf/((6.28+alf)*n*n));
z += (z-x[n-3])*r1*r2*r3;
} else {
z=3.0*x[i-1]-3.0*x[i-2]+x[i-3];
}
alfbet=alf+bet;
for (its=1;its<=MAXIT;its++) {
temp=2.0+alfbet;
p1=(alf-bet+temp*z)/2.0;
p2=1.0;
for (j=2;j<=n;j++) {
p3=p2;
p2=p1;
temp=2.0+j+alfbet;
a=2.0*(j-1+alf)*(j-1+bet)*temp;
b=(temp-1.0)*(alf*alf-beta*beta+temp*(temp-2.0)*z);
c=2.0*(j-1+alf)*(j-1+bet)*temp;
p1=(b*p2-c*p3)/a;
}
// p1 现在是所需的雅可比多项式。接下来利用涉及 p2(低一阶多项式)的标准关系计算其导数 pp。
pp=(n*(alf-bet-temp*z)*p1+2.0*(n+alf)*(n+bet)*p2)/(temp*(1.0-z*z));
z1=z;
z=z1-p1/pp;
if (abs(z-z1) <= EPS) break;
}
if (its > MAXIT) throw("too many iterations in gaujac");
x[i]=z;
w[i]=exp(gammln(alf+n)+gammln(bet+n)-gammln(n+1.0)-gammln(n+alfbet+1.0))*temp*pow(2.0,alfbet)/(pp*pp);
}
}
勒让德多项式是雅可比多项式的特例,对应 ,但为其单独提供上述 gauleg 子程序仍是值得的。切比雪夫多项式对应 (见 §5.8)。它们具有解析形式的横坐标和权重:
4.6.2 已知递推关系的情形
现在考虑这样一种情形:你不知道正交多项式零点的良好初始猜测值,但你拥有生成这些多项式的系数 和 。如前所述, 的零点即为 点高斯求积公式的横坐标。计算权重最有用的公式是上面的公式 (4.6.9),因为导数 在一般情形下可通过 (4.6.6) 的导数高效计算,或对经典多项式使用特殊关系式。注意,(4.6.9) 仅对首一多项式(monic polynomials)成立;对于其他归一化形式,需额外乘以因子 ,其中 是 中 项的系数。
除上述已讨论的特殊情况外,寻找横坐标的最佳方法并非对 使用牛顿法等求根方法。通常更快的方法是使用 Golub-Welsch [3] 算法,该算法基于 Wilf [4] 的一个结果。该算法注意到,若将 (4.6.6) 中的项 移至左边,项 移至右边,则递推关系可写成矩阵形式:
或
其中 是一个三对角矩阵; 是由 构成的列向量; 是一个单位向量,其第 个(即最后一个)分量为 1,其余分量为 0。矩阵 可通过一个对角相似变换 对称化,得到
该矩阵 被称为 Jacobi 矩阵(注意不要与 Jacobi 在其他完全不同的问题中提出的其他同名矩阵混淆!)。现在,从 (4.6.26) 可以看出, 等价于 是 的一个特征值。由于相似变换保持特征值不变,因此 也是对称三对角矩阵 的一个特征值。此外,Wilf [4] 指出,若 是对应于特征值 的特征向量,并且已归一化使得 ,则
其中
且 是向量 的第零个分量。正如我们将在第 11 章看到的那样,求解对称三对角矩阵的所有特征值和特征向量是一个相对高效且数值稳定的算法。因此,我们提供了一个名为 gaucof 的例程,用于在已知系数 和 的情况下计算高斯求积的节点和权重。请注意,如果你知道的正交多项式递推关系中的多项式不是首一的(monic),你可以通过量 轻松将其转换为首一形式。
void gaucof(VecDoub_IO &a, VecDoub_IO &b, const Doub amu0, VecDoub_O &x,
VecDoub_O &w)
gauss_wqts2.h
该函数根据 Jacobi 矩阵计算高斯求积公式的节点和权重。输入时,a[0..n-1] 和 b[0..n-1] 是一组首一正交多项式递推关系的系数。量 以 amu0 输入。返回的节点 x[0..n-1] 按降序排列,对应的权重存于 w[0..n-1] 中。数组 a 和 b 会被修改。若将 tqli 和 eigrsrt 修改为仅计算每个特征向量的第零个分量,则可加快执行速度。
Int n = a.size();
for (Int i = 0; i < n; i++)
if (i != 0) b[i] = sqrt(b[i]);
Symmeig sym(a, b);
for (Int i = 0; i < n; i++) {
x[i] = sym.d[i];
w[i] = amu0 * sym.z[0][i] * sym.z[0][i]; // 公式 (4.6.28)
}
4.6.3 非经典权函数的正交多项式
如果你的权函数不属于上述经典类型,并且你不知道递推关系 (4.6.6) 中的系数 和 以供 gaucof 使用,该怎么办?显然,你需要一种方法来求出这些 和 。
最通用的方法是 Stieltjes 过程:首先由 (4.6.7) 计算 ,然后由 (4.6.6) 计算 。已知 和 后,再由 (4.6.7) 计算 和 ,依此类推。但如何计算 (4.6.7) 中的内积呢?
教科书中的方法是将每个 显式表示为 的多项式,并通过逐项相乘计算内积。如果已知权函数的前 阶矩,
那么这种方法是可行的。然而,用矩 表示系数 和 所得到的代数方程组通常极度病态。即使使用双精度浮点数,当 时也常常完全丧失精度。因此,我们拒绝任何基于矩 (4.6.30) 的方法。
Gautschi [5] 指出,如果 (4.6.7) 中的内积通过数值求积直接计算,则 Stieltjes 过程是可行的。但前提是能找到一种即使在权函数 存在奇点的情况下也能高精度计算积分的求积方案。Gautschi 推荐使用 Fejér 求积法 [5] 作为处理奇点的通用方法(在没有更好方法可用时)。但我们个人在实践中发现,§4.5 中的变量变换方法(尤其是 DE 规则及其变体)效果要好得多。
我们使用一个名为 Stiel 的结构体来实现 Stieltjes 过程。其成员函数 getweights 生成递推关系的系数 和 ,然后调用 gaucof 来计算节点和权重。如果你也需要 和 ,可以轻松修改该结构体以返回这些系数。在内部,该例程调用函数 quad 来计算 (4.6.7) 中的积分。对于有限积分区间,例程使用标准的 DE 规则。此时需用五个参数调用构造函数:所需求积节点(及权重)的数量、积分上下限、传递给 DE 规则的参数 (见 §4.5),以及权函数 。对于无穷积分区间,例程使用 §4.5 中讨论的坐标变换之一结合梯形法则。此时需调用不含 的构造函数,并额外提供映射函数 及其导数 (除了 之外)。此时你输入的积分区间是梯形法则所对应的有限区间。
通过一些例子可以更清楚地理解上述内容。首先考虑权函数
在有限区间 上的情形。通常,对于有限区间情形(DE 规则),权函数需编码为两个变量的函数 ,其中 是到端点奇点的距离。但由于 处的对数奇点是“温和的”,因此在编码该函数时无需使用参数 :
Doub wt(const Doub x, const Doub del)
{
return -log(x);
}
如 §4.5 所述,取 即可达到双精度精度,因此调用代码如下:
n = ...
VecDoub x(n), w(n);
Stiel s(n, 0.0, 1.0, 3.7, wt);
s.getweights(x, w);
对于无穷区间情形,除了权函数 外,还需提供两个函数以指定所用的坐标变换(见公式 4.5.14)。我们将映射 记为 fx, 记为 fdxdt,但你可以使用任意名称。所有这些函数都编码为单变量函数。
以下是一个用户自定义函数的例子,对应权函数
在区间 上的情形。基于 的高斯求积已被提议用于计算广义 Fermi-Dirac 积分 [6](参见 §4.5)。我们使用公式 (4.5.14) 中的“混合”DE 规则:。与 Stieltjes 过程的典型情况一样,当 为几十时,你得到的节点和权重通常能达到机器精度的一到两位有效数字。
Doub wt(const Doub x)
{
Doub s = exp(-x);
return sqrt(x) * s / (1.0 + s);
}
Doub fx(const Doub t)
{
return exp(t - exp(-t));
}
Doub fdxdt(const Doub t)
{
Doub s = exp(-t);
return exp(t - s) * (1.0 + s);
}
...
Stiel ss(n, -5.5, 6.5, wt, fx, fdxdt);
ss.getweights(x, w);
Stiel 对象的完整代码以及对其 C++ 编码中一些细节的讨论见网络附注 [9]。
还有另外两种算法 [7,8] 可用于计算高斯求积的节点和权重。第一种算法与 Stieltjes 过程类似,首先将 (4.6.7) 中的内积积分用某种求积规则离散化。这定义了一个矩阵,其元素由所选求积规则的节点和权重以及给定的权函数构成。然后使用 Lanczos 算法将该矩阵变换为本质上就是 Jacobi 矩阵 (4.6.27) 的形式。
第二种算法基于修正矩(modified moments)的思想。它不用 的幂函数作为表示 的基函数,而是使用另一组已知的正交多项式 。于是 (4.6.7) 中的内积就可以用修正矩表示:
修正的切比雪夫算法(由 Sack 和 Donovan [10] 提出,后经 Wheeler [11] 改进)是一种高效算法,它能从修正矩生成所需的系数 和 。粗略地说,改进后的稳定性之所以更好,是因为在计算内积积分时,该多项式基底对区间 的“采样”效果优于幂基底,尤其是当其权函数与 相似时。该算法要求准确计算修正矩(4.6.33)。有时存在闭式解,例如对于重要的 权函数情形 [12,8]。否则,就必须采用合适的离散化方法来计算修正矩 [7,8],这与我们在 Stieltjes 程序中处理内积的方式类似。选择辅助多项式 需要一定技巧,实践中并不总能找到一组能消除病态条件的多项式。
Gautschi [8] 提供了一套完整的程序,涵盖了我们所描述的三种算法,以及正交多项式和高斯求积的许多其他方面。然而,对于大多数直接的应用,你通常会发现 Stiel 算法配合合适的 DE 规则求积已完全足够。
4.6.4 高斯求积的扩展
高斯求积的思想已被以多种方式加以扩展。其中一个重要扩展是预设节点的情形:要求某些点必须包含在横坐标集合中,问题在于如何选择权重和其余横坐标,以使求积公式的代数精度达到最高。最常见的情形是 Gauss-Radau 求积(其中一个节点为区间端点 或 )和 Gauss-Lobatto 求积(两个端点 和 均为节点)。Golub [13,8] 为这些情形给出了类似于 gaucof 的算法。
一个 点 Gauss-Radau 求积公式具有式 (4.6.1) 的形式,其中 被指定为 或 ( 必须有限)。你可以利用对应的标准 点高斯求积的系数来构造该规则。只需建立 Jacobi 矩阵方程 (4.6.27),但修改其中的元素 :
以下是该例程:
void radau(VecDoub_IO &a, VecDoub_IO &b, const Doub amu0, const Doub x1,
VecDoub_O &x, VecDoub_O &w)
计算 Gauss-Radau 求积公式的横坐标和权重。输入时,a[0..n-1] 和 b[0..n-1] 是对应于权函数的一组首一正交多项式的递推关系系数(b[0] 未被引用)。量 以 amu0 输入。x1 作为区间的任一端点输入。横坐标 x[0..n-1] 以降序返回,对应的权重在 w[0..n-1] 中。数组 a 和 b 会被修改。
Int n = a.size();
if (n == 1) {
x[0] = x1;
w[0] = amu0;
} else {
Doub p = x1 - a[0];
// 通过递推计算 p_{N-1} 和 p_{N-2}
Doub pm1 = 1.0;
Doub p1 = p;
for (Int i = 1; i < n - 1; i++) {
p = (x1 - a[i]) * p1 - b[i] * pm1;
pm1 = p1;
p1 = p;
}
a[n - 1] = x1 - b[n - 1] * pm1 / p;
gaucof(a, b, amu0, x, w);
}
一个 点 Gauss-Lobatto 求积公式具有式 (4.6.1) 的形式,其中 ,(两者均有限)。此时需通过求解两个线性方程来修改方程 (4.6.27) 中的元素 和 :
void lobatto(VecDoub_IO &a, VecDoub_IO &b, const Doub amu0, const Doub x1, const Doub xn,
VecDoub_O &x, VecDoub_O &w)
计算 Gauss-Lobatto 求积公式的横坐标和权重。输入时,向量 a[0..n-1] 和 b[0..n-1] 是对应于权函数的一组首一正交多项式的递推关系系数(b[0] 未被引用)。量 以 amu0 输入。x1 和 xn 作为区间的两个端点输入。横坐标 x[0..n-1] 以降序返回,对应的权重在 w[0..n-1] 中。数组 a 和 b 会被修改。
Doub det, pl, pr, p11, p1r, pm11, pm1r;
Int n = a.size();
if (n <= 1)
throw("n must be bigger than 1 in lobatto");
pl = x1 - a[0];
pr = xn - a[0];
Doub pm1 = 1.0;
pm11 = pm1;
pm1r = pm1;
p11 = pl;
p1r = pr;
for (Int i = 1; i < n - 1; i++) {
pl = (x1 - a[i]) * p11 - b[i] * pm11;
pr = (xn - a[i]) * p1r - b[i] * pm1r;
pm11 = p11;
pm1r = p1r;
p11 = pl;
p1r = pr;
}
det = p11 * pm1r - pr * pm11;
a[n - 1] = (x1 * p11 * pm1r - xn * pr * pm11) / det;
b[n - 1] = (xn - x1) * p11 * pr / det;
gaucof(a, b, amu0, x, w);
高斯求积的第二个重要扩展是 Gauss-Kronrod 公式。对于普通高斯求积公式,当 增加时,横坐标集合之间没有公共点。这意味着,若通过比较不同 下的结果来估计求积误差,则无法重用之前的函数求值结果。Kronrod [14] 提出了寻找最优规则序列的问题,其中每个规则都重用其前一个规则的所有横坐标。例如,若从 开始,再增加 个新点,则共有 个自由参数: 个新横坐标及其权重,以及 个已有横坐标对应的新权重。因此,预期能达到的最大代数精度为 。问题是,当所有横坐标都必须位于 内部时,是否真能实现这一最大精度。这个问题在一般情况下尚无定论。
Kronrod 证明,若选择 ,则可为 Gauss-Legendre 求积找到最优扩展。Patterson [15] 展示了如何计算此类连续扩展。诸如 的序列在自动求积程序 [16] 中很受欢迎,这些程序试图对函数进行积分,直到达到指定的精度为止。
参考文献
Abramowitz, M., and Stegun, I.A. 1964, Handbook of Mathematical Functions (Washington: National Bureau of Standards); reprinted 1968 (New York: Dover); online at http://www.nr.com/aands, §25.4.[1]
Stroud, A.H., and Secrest, D. 1966, Gaussian Quadrature Formulas (Englewood Cliffs, NJ: Prentice-Hall).[2]
Golub, G.H., and Welsch, J.H. 1969, "Calculation of Gauss Quadrature Rules," Mathematics of Computation, vol. 23, pp. 221–230 and A1–A10.[3]
Wilf, H.S. 1962, Mathematics for the Physical Sciences (New York: Wiley), Problem 9, p. 80.[4]
Gautschi, W. 1968, "Construction of Gauss-Christoffel Quadrature Formulas," Mathematics of Computation, vol. 22, pp. 251–270.[5]
Sagar, R.P. 1991, "A Gaussian Quadrature for the Calculation of Generalized Fermi-Dirac Integrals," Computer Physics Communications, vol. 66, pp. 271–275.[6]
Gautschi, W. 1982, "On Generating Orthogonal Polynomials," SIAM Journal on Scientific and Statistical Computing, vol. 3, pp. 289–317.[7]
Gautschi, W. 1994, "ORTHPOL: A Package of Routines for Generating Orthogonal Polynomials and Gauss-type Quadrature Rules," ACM Transactions on Mathematical Software, vol. 20, pp. 21–62 (Algorithm 726 available from netlib).[8]
Numerical Recipes Software 2007, "Implementation of Stiel," Numerical Recipes Webnote No. 3, at http://www.nr.com/webnotes?3 [9]
Sack, R.A., and Donovan, A.F. 1971/72, "An Algorithm for Gaussian Quadrature Given Modified Moments," Numerische Mathematik, vol. 18, pp. 465–478.[10]
Wheeler, J.C. 1974, "Modified Moments and Gaussian Quadratures," Rocky Mountain Journal of Mathematics, vol. 4, pp. 287–296.[11]
Gautschi, W. 1978, in Recent Advances in Numerical Analysis, C. de Boor and G.H. Golub, eds. (New York: Academic Press), pp. 45–72.[12]
Golub, G.H. 1973, "Some Modified Matrix Eigenvalue Problems," SIAM Review, vol. 15, pp. 318–334.[13]
Kronrod, A.S. 1964, Doklady Akademii Nauk SSSR, vol. 154, pp. 283–286 (in Russian); translated as Soviet Physics “Doklady”.[14]
Patterson, T.N.L. 1968, "The Optimum Addition of Points to Quadrature Formulae," Mathematics of Computation, vol. 22, pp. 847–856 and C1–C11; 1969, op. cit., vol. 23, p. 892.[15]
Piessens, R., de Doncker-Kapenga, E., Überhuber, C., and Kahaner, D. 1983 QUADPACK, A Subroutine Package for Automatic Integration (New York: Springer). Software at http://www.netlib.org/quadpack.[16]
Gautschi, W. 1981, in E.B. Christoffel, P.L. Butzer and F. Fehér, eds. (Basel: Birkhäuser), pp. 72–147.
Gautschi, W. 1990, in Orthogonal Polynomials, P. Nevai, ed. (Dordrecht: Kluwer Academic Publishers), pp. 181–216.
Stoer, J., and Bulirsch, R. 2002, Introduction to Numerical Analysis, 3rd ed. (New York: Springer) §3.6.
4.7 自适应积分
自适应积分背后的思想非常简单。假设你有两个不同的数值估计 和 ,用于计算积分
假设 更精确。利用 与 之间的相对差值作为误差估计。如果该差值小于 ,则接受 作为结果;否则将区间 分成两个子区间,
并分别计算这两个积分。对每个子区间,分别计算 和 ,估计误差,并在必要时继续细分。当某个子区间的误差贡献相对于 足够小时,就停止对该子区间的进一步细分。(显然,递归是实现该算法的良好方式。)
自适应积分程序最重要的标准是可靠性:如果你要求精度为 ,你希望确保结果至少达到该精度。然而,从理论角度看,不可能设计出适用于所有可能函数的自适应积分程序。原因很简单:数值积分基于被积函数 在有限个点上的取值。你可以在所有其他点上任意修改函数,而不会影响算法返回的估计值,但积分的真实值却可能不可预测地改变。尽管存在这一理论上的限制,但在实践中,优秀的程序对它们遇到的绝大多数函数都是可靠的。我们偏好的程序是 Gander 和 Gautschi [1] 提出的方法,下面将对其进行描述。该方法相对简单,但在可靠性和效率方面表现良好。
一个好的自适应算法的关键组成部分是终止准则。常用的准则
存在问题。在奇点附近,即使所要求的容差并不特别小, 和 也可能永远无法满足该容差。因此,你需要设法对整个积分 (见公式 (4.7.1))给出一个估计值 。然后,当 的误差相对于整个积分可以忽略不计时终止计算:
其中 是对 的估计。Gander 和 Gautschi 通过如下代码实现该测试:
if (is + (i1 - i2) == is)
这相当于将 设为机器精度。然而,现代优化编译器过于“聪明”,会识别出这在代数上等价于
if (i1 - i2 == 0.0)
而在浮点运算中,这种情况可能永远不会满足。因此,我们在实现中显式地使用一个 。
另一个需要注意的问题是,当某个区间被细分到其内部不再包含任何机器可表示的点时,你需要终止递归,并提醒用户可能未达到所需的全部精度。例如,若某区间的点应为 ,你可以检测是否满足 或 。
Gander-Gautschi 方法中最低阶的积分公式是四点 Gauss-Lobatto 求积公式(参见 §4.6):
该公式对五次多项式是精确的,用于计算 。为了在计算 时重用这些函数求值,他们采用了七点 Kronrod 扩展:
该公式的代数精度为九次。公式 (4.7.5) 和 (4.7.6) 可从区间 缩放到任意子区间 。
对于 ,Gander 和 Gautschi 进一步构造了公式 (4.7.6) 的 13 点 Kronrod 扩展,从而可以重用之前的函数求值。该公式已编码到下面的例程中。你可以将这最初的 13 点求值视为一种蒙特卡洛采样,用以估计积分的大致量级。但如果被积函数是光滑的,这一初始估计本身就已经相当精确了。下面的例程充分利用了这一点。
注意,为了在七点公式 (4.7.6) 中重用公式 (4.7.5) 中的四个函数求值,你不能简单地对区间进行二分。但将其划分为六个子区间是可行的(七个点之间正好有六个区间)。
要使用该例程,你需要用所需的容差初始化一个 Adapt 对象:
Adapt s(1.0e-6);
然后调用 integrate 函数:
ans = s.integrate(func, a, b);
你应该检查是否达到了所需的容差:
if (s.out_of_tolerance)
outs << "Required tolerance may not be met" << endl;
允许的最小容差为机器精度的 10 倍。如果你输入了更小的容差,程序内部会自动将其重置。(该例程也可以使用机器精度本身工作,但通常只会导致大量函数求值,而几乎没有额外收益。)
Adapt 对象的实现见网络附注 [2]。
自适应积分并非万能良药。上述例程除了对邻近区间进行细化外,并没有专门处理奇点的机制。通过为 和 选用合适的方案,可以定制自适应例程以处理特定类型的奇点(参见 [3])。
参考文献
Gander, W., and Gautschi, W. 2000, "Adaptive Quadrature — Revisited," BIT vol. 40, pp. 84-101. [1]
Numerical Recipes Software 2007, "Implementation of Adapt," Numerical Recipes Webnote No. 4, at http://www.nr.com/webnotes?4 [2]
Piessens, R., de Doncker-Kapenga, E., Überhuber, C., and Kahaner, D. 1983 QUADPACK, A Subroutine Package for Automatic Integration (New York: Springer). Software at http://www.netlib.org/quadpack. [3]
Davis, P.J., and Rabinowitz, P. 1984, Methods of Numerical Integration, 2nd ed., (Orlando, FL: Academic Press), Chapter 6.
4.8 多重积分
对多变量函数在维度大于一的区域上进行积分并不容易,原因有二。首先,为了对 维空间进行采样,所需的函数求值次数随一维积分所需次数的 次方增长。例如,若粗略计算一个一维积分需要 30 次函数求值,那么要达到同样粗略的精度,三维积分可能就需要大约 30000 次求值。其次, 维空间中的积分区域由一个 维的边界所定义,而该边界本身可能极其复杂:例如,它未必是凸的,也未必是单连通的。相比之下,一维积分的边界仅由两个数(即上下限)构成。
面对一个多重积分时,首先要问的问题是:能否通过解析方法将其降维?例如,所谓的一元函数 的迭代积分(iterated integrals)可通过以下公式化为一维积分:
或者,函数在其自变量上的依赖关系可能具有某种特殊对称性。如果积分区域也具有这种对称性,则可降低积分维度。例如在三维空间中,若对一个球对称函数在球形区域上积分,则在球坐标系下可简化为一维积分。
接下来的问题将引导你在两种截然不同的方法之间做出选择。这些问题包括:积分区域边界的形状是简单还是复杂?在区域内,被积函数是光滑简单的,还是复杂的,或是在局部有强烈的尖峰?该问题是否要求高精度,还是只需百分之一或几个百分点的精度即可?
如果你的答案是:边界复杂、被积函数在很小区域内没有强烈尖峰、且可接受较低精度,那么你的问题就非常适合采用蒙特卡罗积分(Monte Carlo integration)。这种方法在较粗糙的形式下编程非常直接:你只需知道一个包含复杂积分区域的、具有简单边界的区域,并具备判断一个随机点是否位于积分区域内部的方法即可。蒙特卡罗积分通过对随机采样点处的函数值进行评估,并基于这些样本估计积分值。我们将在第 7 章中更详细、更深入地讨论该方法。
如果边界简单,且函数非常光滑,那么其余方法——将问题分解为重复的一维积分,或使用多维高斯求积法——将是高效且相对快速的 [1]。如果你需要高精度,那么这些方法是你唯一的选择,因为蒙特卡罗方法本质上收敛速度较慢。
对于低精度需求:若被积函数在积分区域内变化缓慢且光滑,则使用重复的一维积分或多维高斯求积;若被积函数振荡或不连续,但在小区域内没有强烈尖峰,则使用蒙特卡罗方法。
如果被积函数在小区域内有强烈尖峰,且你知道这些区域的位置,则可将积分拆分为若干子区域,使得每个子区域内的被积函数都是光滑的,并分别计算。如果你不知道这些尖峰区域的位置,那么(以本书的复杂度水平而言)你最好放弃:期望一个积分程序在巨大的 维空间中自动搜寻未知的、贡献巨大的“口袋”是毫无希望的。(但参见 §7.9。)
如果你根据上述准则决定采用重复的一维积分方法,其工作方式如下。为明确起见,我们考虑 、、 空间中的三重积分。二维或高于三维的情形与此完全类似。
第一步是通过以下方式指定积分区域:(i) 的下限和上限,记为 和 ;(ii) 在给定 值下 的下限和上限,记为 和 ;(iii) 在给定 和 下 的下限和上限,记为 和 。换句话说,找出数值 、 以及函数 、、、,使得
例如,对以原点为中心、半径为 1 的圆进行二维积分可写为:
现在我们可以定义一个函数 来计算最内层积分:
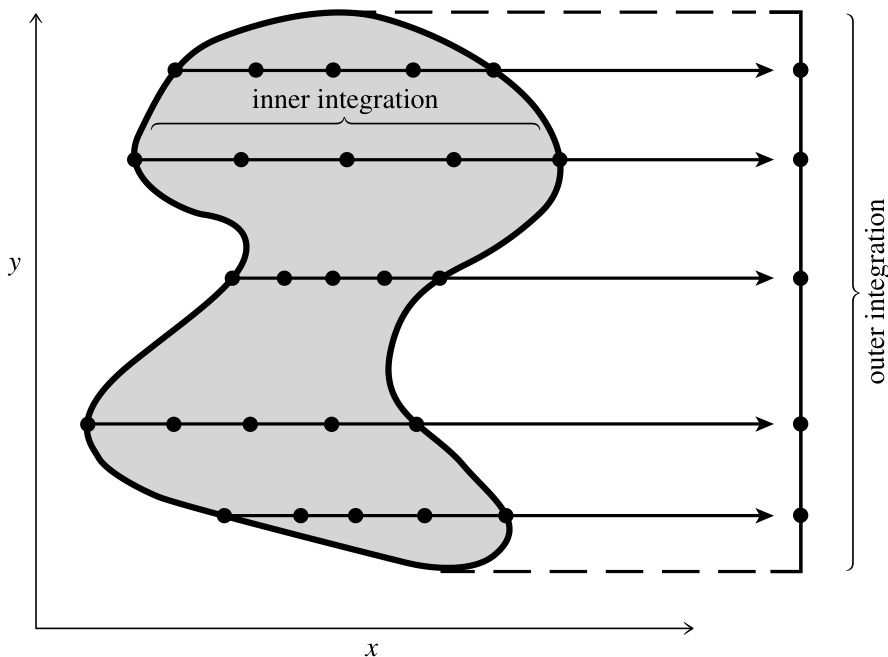
图 4.8.1. 对不规则区域进行二维积分时的函数求值示意图。外层积分程序(对 )在其自行选择的 轴位置上请求内层(对 )积分的值。内层积分程序随后在适合自己的 位置上对函数求值。这种方法通常比在笛卡尔网格点上求值更精确。
再定义一个函数 来对 积分:
最后,我们的答案即为对 的积分:
在实现公式 (4.8.4)–(4.8.6) 时,某个基本的一维积分程序(例如下面程序中的 qgaus)会被递归调用:一次用于计算最外层积分 ,多次用于计算中间层积分 ,更多次用于计算最内层积分 (见图 4.8.1)。当前的 和 值,以及用户提供的被积函数和边界函数的指针,通过定义 、 和 被积函数的三个函子(functor)的成员变量,“越过”中间调用层级进行传递。
struct NRf3 {
Doub xsaav,ysav;
Doub (*func3d)(const Doub, const Doub, const Doub);
Doub operator()(const Doub z) // 在固定的 x 和 y 下计算被积函数 f(x,y,z)
{
return func3d(xsaav,ysav,z);
}
};
struct NRf2 {
NRf3 f3;
Doub (*z1)(Doub, Doub);
Doub (*z2)(Doub, Doub);
NRf2(Doub zz1(Doub, Doub), Doub zz2(Doub, Doub)) : z1(zz1), z2(zz2) {}
Doub operator()(const Doub y) // 这是公式 (4.8.4) 中的 G
{
f3.ysaav=y;
return qgaus(f3,z1(f3.xsaav,y),z2(f3.xsaav,y));
}
};
struct NRf1 {
Doub (*y1)(Doub);
Doub (*y2)(Doub);
NRf2 f2;
NRf1(Doub yy1(Doub), Doub yy2(Doub), Doub z1(Doub, Doub),
Doub z2(Doub, Doub)) : y1(yy1),y2(yy2), f2(z1,z2) {}
Doub operator()(const Doub x) // 这是公式 (4.8.5) 中的 H
{
f2.f3.xsaav=x;
return qgaus(f2,y1(x),y2(x));
}
};
template <class T>
Doub quad3d(T &func, const Doub x1, const Doub x2, Doub y1(Doub), Doub y2(Doub),
Doub z1(Doub, Doub), Doub z2(Doub, Doub))
// 返回用户提供的函数 func 在由 x1, x2 以及用户提供的函数 y1, y2, z1, z2
// 所定义的三维区域上的积分,如 (4.8.2) 所示。通过递归调用 qgaus 进行积分。
{
NRf1 f1(y1,y2,z1,z2);
f1.f2.f3.func3d=func;
return qgaus(f1,x1,x2);
}
注意,虽然被积函数既可以作为简单函数提供:
Doub func(const Doub x, const Doub y, const Doub z);
也可以作为等效的函子提供,但定义边界的函数只能是普通函数:
Doub y1(const Doub x);
Doub y2(const Doub x);
Doub z1(const Doub x, const Doub y);
Doub z2(const Doub x, const Doub y);
这是为了简化实现:如果你需要,可以轻松修改代码以支持函子。
quad3d 中使用的高斯求积程序很简单,但其精度不可控。另一种选择是使用像 qtrap、qsimp 或 qromb 这样具有用户可定义容差 eps 的一维积分程序。例如,只需将 quad3d 中所有 qgaus 的调用替换为 qromb 即可。
注意,如果你对精度要求过高,多重积分可能会非常缓慢。你几乎肯定需要将 qromb 中默认的 eps 从 提高到 或更大。你还应减小 JMAX 以避免长时间等待结果。有些人建议对内层求积(在我们的程序中是对 的积分)使用比外层求积(对 或 )更小的 eps。
参考文献
Stroud, A.H. 1971, Approximate Calculation of Multiple Integrals (Englewood Cliffs, NJ: Prentice-Hall). [1]
Dahlquist, G., and Bjorck, A. 1974, Numerical Methods (Englewood Cliffs, NJ: Prentice-Hall); 2003 年重印 (New York: Dover), §7.7, p. 318.
Johnson, L.W., and Riess, R.D. 1982, Numerical Analysis, 2nd ed. (Reading, MA: Addison-Wesley), §6.2.5, p. 307.
Abramowitz, M., and Stegun, I.A. 1964, Handbook of Mathematical Functions (Washington: National Bureau of Standards); 1968 年重印 (New York: Dover); 在线版见 http://www.nr.com/aands, 公式 25.4.58ff.